稚化思维促进数学课堂的两种生长<br/>——一次同课异构课引发的反思

稚化思维促进数学课堂的两种生长
——一次同课异构课引发的反思

2017-08-23安徽省合肥市第三十二中学李启梅邮编230051

中学数学教学 2017年4期

安徽省合肥市第三十二中学李启梅 (邮编:230051)

稚化思维促进数学课堂的两种生长
——一次同课异构课引发的反思

安徽省合肥市第三十二中学李启梅 (邮编:230051)

对华东师范大学李政涛教授报告《让课堂散发生长的气息》中提出的好课的最后一个标准,即“教学有无生长感”的观点深有感触,最近阅读多篇有关稚化思维的文章.认为在稚化思维策略下的数学课堂应像著名特级教师薛法根所说:课堂,呈现的不仅仅是鲜花,还有花开的声音,最美的声音是学生生命里拔节的声音.那么什么是稚化思维?

稚化思维,简言之,就是教师有意识将自己的思维降到学生的思维水平,甚至更低,设身处地地揣摩学生的思维活动和学习过程,以与学生同样的兴趣、同样的思维,通过共同探究力求达到与学生思维共振,共创教学和谐.它的作用在于:有利于降低学生的认知难度;有利于拉近师生情感距离;有利于引起师生思维共振.

下面运用稚化思维策略对一次区级范围内的同课异构课进行改进,以和同仁共勉.

1 教学片段

两位老师同上了一节人教A版必修5《3.4基本不等式》这节内容,下面节选两节课中基本不等式的引入和应用的课堂实录.

实录1

片段1 引入

师:(简单介绍第24届国际数学家大会的会标)你能在这个图案中找出一些相等关系或不等关系吗?

生:一片默然(问题指向不够明确).

师:四个直角三角形面积相等,和大正方形面积相比,有a2＋b2≥2ab,(动画展示中间小长方形逐步缩成一点),当a＝b时取等号.

师:这就是重要不等式:一般的,如果a、b∈R,则a2＋b2≥2ab.

学生上黑板板演证明过程,师生共同评讲.

片段2 应用

师:下面我们来看基本不等式的简单应用:例(1)用篱笆围成一个面积100m2的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短.最短的篱笆是多少?(2)用一段长为36m的篱笆围成一个矩形菜园,问这个矩形菜园的长和宽各为多少时,菜园的面积最大,最大面积是多少?

生:(大部分同学感觉不知从哪下手,教室里很安静).

教师展示解答,快速讲解.

实录2

片段1 引入

师:(简单介绍第24届国际数学家大会的会标及数学的最高奖项－－菲尔兹奖)观察图1中的四个小直角三角形和大正方形面积的大小关系.

生:S正方形＞4S三角形.

师:再看图2中圆的半弦CD和半径的关系.

生:半弦CD小于半径.

从而引入了重要不等式和基本不等式.

片段2 应用

例1 若a、b、c是互不相等的实数,求证:a2＋b2＋c2＞ab＋bc＋ca.

学生不知从何做起.

例2 已知a、b、c∈R＋,且a＋b＋c＝1,求证

下课铃声响起,例2没

有时间证明.

2 教学反思

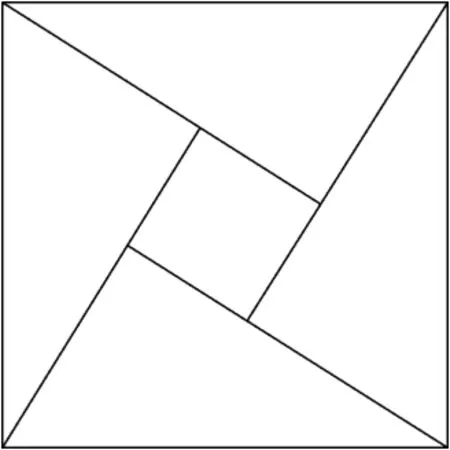
图1

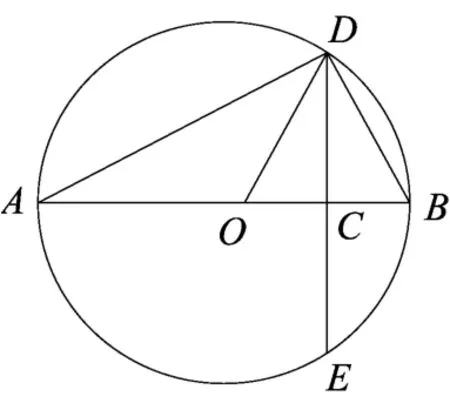
图2

两位老师在处理教材上截然不同,教学风格也大相径庭,给人留下了深刻的印象.表面上两位老师课堂设计似乎没有问题,特别是第二位老师处理得似乎很独特,但从教材和学生两方面深入思考,笔者认为:

第一位老师由会标图形引出了重要不等式,由于图形中a、b∈R＋,如何过渡a、b∈R?这是学生想知道的,这个条件不能硬塞给学生;同时为什么取等号也需要学生积极去建构,而不是老师一个动画展示所能代替的.在例题的设计上,由于这是一个普通高中,应用题的解答对学生来说一直就是一个难点,因而可以先设计有一定坡度的引例作为铺垫,再来解决实际问题,比较切合学生的认知.

第二位老师突出两个不等式的几何意义,对比教学,创意虽好,但割裂了重要不等式和基本不等式的关系,体现不到代数变换,也违背了教材编写者的初衷,给学生感觉它们是相互独立的,特别是例题的设计远远超出了学生的实际水平.

他们在备课时忽视了两个问题:知识在课堂中如何自然生长和新知识在学生的认知结构中怎样新生长.课堂生长的前提,一是认真解读课程标准和教材,二是基于学生立场,认真解读学生.学生实际状态应成为教育教学的起点和出发点,是教学目标制定的依据.为此,教师可以退回到学生相仿的思维,接地气地来熟读教材,谙熟学情.

3 改进

稚化思维后的数学教学,应关注两种“生长”,即知识自然展开的“自生长”和知识在学生认知中“新生长”.从数学角度看,它合乎数学知识本身的逻辑结构和发展规律;从学生角度来看,它合乎他们的认知规律和心理特征.因而教师备课时要研究这部分知识的逻辑关系和学生原有认知是什么.

(1)遵循逻辑关系,促进知识的自生长

数学知识之间有内在的逻辑关系,这些关系对学生来说,都是陌生的.因而需要教师从学情出发,贴近学生的认知,降低思维,在学生的最近发展区思考:如何将这些知识自然地展开?如何促进知识在学生原有知识基础上生根发芽?

我们知道基本不等式的引入是建立在重要不等式的基础上,而重要不等式的得出经历了图形的直观感知到数学的严格证明,在证明的过程中引导发现a、b的范围,从而由正实数推广到全体实数.再用代数变换导出了基本不等式,由此可以作以下展开:

师:(简单介绍第24届国际数学家大会的会标及数学的最高奖项菲尔兹奖)观察会标有哪些图形构成?若四个小直角三角形面积相等,那么四个直角三角形的面积和大正方形面积的大小关系如何呢?

生:正方形和直角三角形;S正方形＞4S三角形.

师:a2＋b2＞2ab,追问:a2＋b2能和2ab相等吗?什么情况下相等?

让学生观察图形直观想象,由问题启动思维,展开新知.

师:在学生初步形成结论后动画展示,中间小正方形缩成一个点,此时a＝b.

此时学生完成了对重要不等式的直观感知,而这种由特殊图形得出结论还需理论上的证明和进一步的完善.

师:这里a、b∈R＋,这个结论可靠吗?你打算怎样证明?

生:作差比较.

师:你发现作差变形后竟是一个实数的平方,显然大于等于0,既然这样,对a、b∈R,结论还成立吗?

生:当然成立(异口同声).

师:显然这里a、b为非负数.

设计意图:按照两不等式的内在逻辑关系,通过不断地创设问题情境,搭建“脚手架”,降低认知难度,使得两不等式的关系清晰,基本不等式自然生成.

(2)遵循认知特点,促进知识的新生长

在稚化思维下,要求教师把思维的触角深入到学生的思维领地,进行发掘和研究,想学生所想,惑学生所惑.正如特级教师魏书生曾说过:“知识是生长出来的”.学生对新知识的理解是逐步由模糊到清晰、由零碎到完整并逐步融入原有知识体系之中,在原有基础上进行的老枝发新芽.学生在学习这部分知识前已学习:一个实数的平方大于等于0;不等式的性质;不等式的解法;线性规划.在此基础上对不等式作进一步研究,介绍利用基本不等式求一类函数的最值.

如果把学生认知中的不等式知识看作一根老枝的话,那么通过本节课的学习,它应经历了三次成长,首先是认识基本不等式的形式和特征;其次从数学角度对它进行第二次认识,理解一正和二定的含义;再次从数学应用的角度进行再认识,理解三相等以及积定和最小,和定积最大,体会基本不等式的作用.在知识的自然展开中,学生认识了基本不等式,通过三次成长,新知识在学生原有的知识上发芽.学生第一次接触基本不等式,理解它已很困难,对于应用则是更高层次的要求.因而要增设一些坡度,通过适当的变式,引起学生认知冲突,加深理解,逐步爬坡,最后学以致用.

师:是否还需作差比较?

生:不需要,用基本不等式.

师:基本不等式反映的是两正实数和积之间的关系,两正实数的积有定值吗?

生:有,是2.

师:若x＜0呢?能用基本不等式吗?为什么?(对a、b∈R＋再认识)

例2 (1)在学校操场边,有一块面积为100m2的荒地,为了美化校园环境,学校决定用篱笆围起来,问这个矩形的长、宽各为多少时,所用篱笆最短.最短的篱笆是多少?

(2)学校宿舍区有一段长为36m的篱笆,要围成一个矩形花坛,问这个矩形的长、宽各为多少时,花坛的面积最大.最大面积是多少?

师:设长为x,宽为多少?最短篱笆长又为多少?

(到此学生在例1的基础上,顺势而上,对基本不等式的认识进行了积极的同化)

师:在(2)中很容易得出花坛的面积S＝x (18－x),由x与18－x形成的积式,它们的和有定值吗?

设计意图:例1设计便于学生对基本不等式的应用条件、结构特征的进一步理解,对用基本不等式求最值时的“一正”,“二定”的准确理解,为例2打下基础.例2为“三相等”顺利实行新知识的同化,促进知识的新生长.

稚化思维的设计遵循了知识的内在结构,知识发生、发展的历程,及时扫清了学生认知的障碍,调动了学生情感的参与.有效地促进知识在课堂的“自生长”和知识在学生认知中“新生长”,以达到自然的教学,这正是我们每位老师追求的教学的至高艺术!