挖掘问题隐含条件的解题策略

安徽省六安市清水河学校 杨玉峰 (邮编:237000)

挖掘问题隐含条件的解题策略

安徽省六安市清水河学校 杨玉峰 (邮编:237000)

在数学解题过程中,我们要充分利用题目的条件,但是有些问题的条件不是显在的,而是隐含的,需要我们挖掘其隐含条件,才能顺利地解答.下面我们结合几个具体实例说明,供参考.

1 利用概念特性,挖掘隐含条件

这一类型的题目相对比较容易发现其中的隐含条件,只要吃透数学概念的本质属性,并善于归纳、总结,容易找到解决问题的方法.

解析 解决本题的关键是要求出x、y、z的值,而已知方程一个关于x、y、z的三元方程,一般情况下难以求出它们的值.本题的隐含条件是(x－6)2,,3y＋2z 具有非负性,又(x－6)2＋＋3y＋2z＝0,所以有(x－6)2＝0,＝0, 3y＋2z ＝0,即x＝6,y＝2,z＝－3,故(x－y)2－z2＝7.

2 关注变量范围,挖掘隐含条件

这类题目的隐含条件存在于题设之中,往往不被学生注意,特别是题中的参数取值范围,极易被忽视.凡涉及多个参数或变量问题,务必注意范围优先的原则.

例2 已知x1、x2是方程x2－(k－4)x＋(k2＋2k＋8)＝0的两根,求x21＋x22的最大值.

解析 若不找出隐含条件,下面的解法是错误的:x21＋x22＝(x1＋x2)2－2x1x2＝(k－4)2－2(k2＋2k＋8)＝－k2－12k＝－(k＋6)2＋36.

所以最大值为36.当且仅当k＝－6时,取得最大值.

上述解法错误的原因是没有挖掘隐含条件:△＝(k－4)2－4(k2＋2k＋8)≥0,即－4≤k,所以当k＝－4时,才取得最大值32.

3 利用恒等变形,挖掘隐含条件

这类题目的隐含条件藏在已知等式或不等式之中,比较难以发现,利用式子的恒等变形,将所给的式子朝着有利于解题方向变形,从而挖掘出隐含条件.

例3 若3(a2＋b2＋c2)＝(a＋b＋c)2(a≠0),求的值.

解析 将已知条件变形,得2(a2＋b2＋c2－ab－bc－ca)＝(a－b)2＋(b－c)2＋(c－a)2＝0,得a＝b＝c,这是本题隐含的条件,从而可得

4 借助数形结合,挖掘隐含条件

平面几何题是初中数学的难点,解决有些几何问题的关键条件往往隐藏在几何图形中及已知条件的背后,这就需要我们大胆猜测,数形结合,从而挖掘出问题的隐含条件.

例4 (2017年安徽省中考数学第10题)如图,在矩形ABCD中,AB＝5,AD＝3,动点P满足,则点P到A、B两点距离之和PA＋PB的最小值为( )

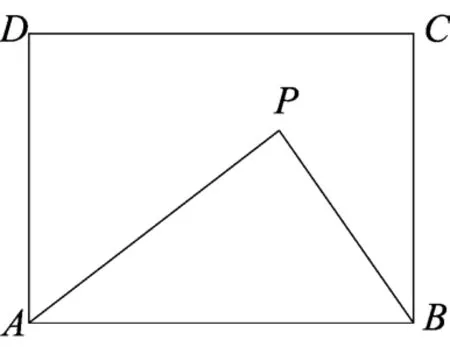
解析 设点P到AB的距离为h,由S△PAB＝,得所以动点P在与AB平行且距离为h的直线上.设此直线为l,问题转化为:在直线l上求一点P,使得PA＋PB取得最小值.作点B关于直线l的对称点B′,连接AB′,则AB′的长就是PA＋PB的最小值.据对称性可得,,再由勾股定理,得AB′＝,故PA＋PB的最小值为.此题的本质是一个典型的最值模型:在直线l上求一点P,使得PA＋PB取最小值.而本题利用图形面积关系,巧妙地将点P在一条直线上的这一条件“隐藏”起来,解题时首先要将此隐含条件挖掘出来,否则无法往下进行.

数学题目中的隐含条件往往是解题的关键,由于隐含条件的隐蔽性,我们往往不容易看出来.如果不能挖掘出关键的隐含条件,解题就会卡住,一筹莫展.这就要求教师除了教会学生过硬的基础知识和基本技能外,还必须培养他们严谨的思维方法和敢于发现问题的能力,方能达到事半功倍的教学效果.

2017-07-04)