关于有心圆锥曲线两条性质的注记

武汉市武汉外国语学校(430022) 李彬

关于有心圆锥曲线两条性质的注记

武汉市武汉外国语学校(430022) 李彬

圆,椭圆,双曲线均是具有对称中心的二次曲线,我们将之统称为有心圆锥曲线.为了方便我们将其在平面直角坐标系中的标准方程统一记为:

其中a,b＞0,ε=0或1.

性质1两条位似的有心圆锥曲线C1,C2以对称中心为位似中心,若直线l与C1交于P,Q两点,与C2交于S,T两点,则|PS|=|TQ|.

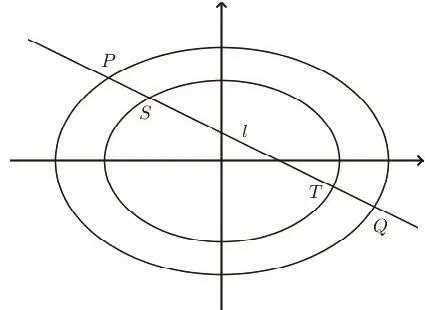
图1

图2

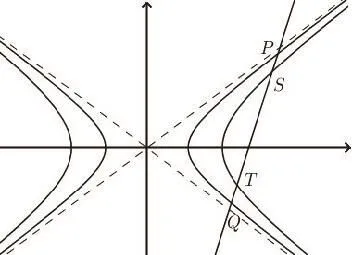
图3

证明设C1,C2在平面直角坐标系中方程如下:

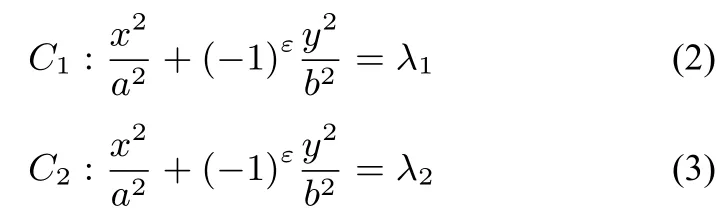
其中λ1,λ2＞0.当直线l垂直于x轴时结论显然.否则,设直线l方程为:y=kx+d分别代入(2),(3)可得到关于x的两个二次方程.易知这两个二次方程二次项系数(均非0,因有两个交点)和一次项系数分别对应相等,故由韦达定理可知:

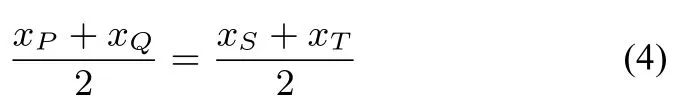
即线段PQ和ST中点相同,从而|PS|=|TQ|.

注1.当(2),(3)中ε=0且a=b(即C1,C2为两个同心圆)时,此结论由平面几何知识是显然的.

2.当(2),(3)中ε=0且a≠b(即C1,C2为两个位似的椭圆)时,可通过伸缩变换

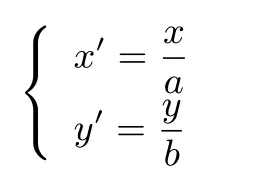
将C1,C2变为两个同心圆,再由注1即得(伸缩变换后线段PS和TQ变为被同心圆截得的两条线段P′S′和T′Q′,且

3.当(2),(3)中ε=1(即C1,C2为两个位似的双曲线)时,固定λ1,令λ2趋向于0,则极限情形时C2为C1的渐近线,由性质1可知:直线l截双曲线及其渐近线,夹于双曲线和渐近线间的线段长度相等.

性质2有心圆锥曲线D1,D2方程如下:

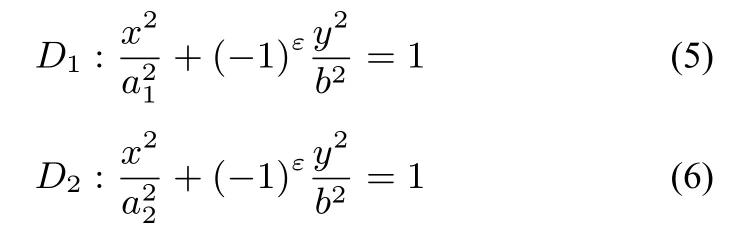
若直线l与D1交于P,Q两点,与D2交于S,T两点且P,Q,S,T均不在y轴上,则

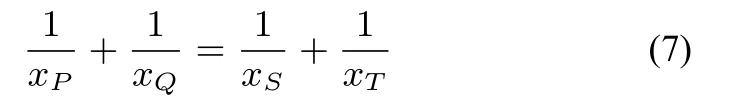
证明当直线l垂直于x轴时结论显然.否则,设直线l方程为:y=kx+b分别代入(5),(6)可得到关于x的两个二次方程.易知这两个二次方程一次项系数和常数项分别对应相等,二次项系数不等且均非0(因有两个交点),故由韦达定理可知:

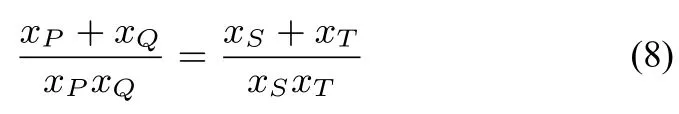
化简即得(7).

注若直线l斜率存在,设其与y轴交于点R(0,yR).

1.当ε=1(D1,D2均为双曲线,见图4),或ε=0(D1,D2均为椭圆或圆)且R在D1,D2外时(见图5),点R关于D1,D2的切点弦 (或称为极线)相同,均为设l2与l交点为M,则R,P,M,Q构成调和点列,R,S,M,T也构成调和点列.可知点M的横坐标xM既为P,Q横坐标的调和平均数,又为S,T横坐标的调和平均数,即

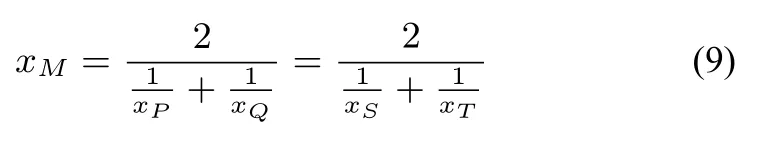
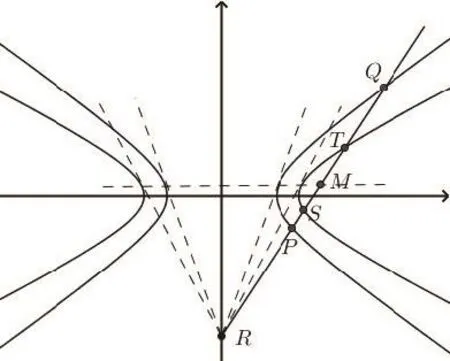
图4

图5

上述两条关于有心圆锥曲线的性质都是关心直线与有心圆锥曲线的两个交点的横坐标所满足的关系.当圆锥曲线满足特定的条件时,性质1中两个交点横坐标的代数平均值为常数,性质2中两个交点横坐标的调和平均值为常数,看上去两个性质的条件也好、结论也罢有相似之处,但又是截然不同的,似乎有着千丝万缕的联系,从我们给出的两个具有异曲同工之妙的证明来看也印证了这一点.下面我们将从坐标变换的角度来解释两条性质之间的关系.

考虑对平面直角坐标系作如下的坐标变换:

注意坐标变换(11)是将平面上所有不在y轴上的点构成的点集映到自身的一个双射.该变换将平行于y轴的直线m:x=d(d≠0)变为直线m′:将挖掉点(0,d)的直线n:y=kx+d变为挖掉点(0,k)的直线n′:y′=dx′+k.

注下文中在不引起混淆的情况下,将经坐标变换(11)后得到的曲线方程中x′,y′的直接写作x,y.另外,下文中提到经坐标变换(11)某曲线C变为曲线C′时,不再特别指出需去掉C及C′与y轴的交点.

性质1中的有心圆锥曲线

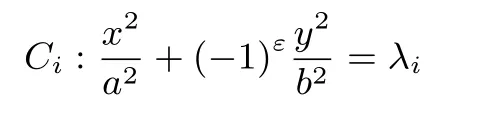
经坐标变换(11)变为:

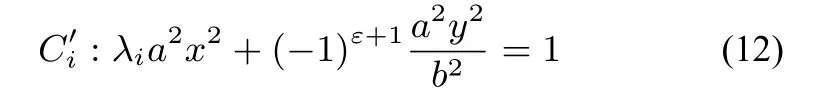
符合性质2中的条件.注意(11)将椭圆或圆变作双曲线,将双曲线变作椭圆或圆,另外性质1中的直线仍变作直线.若性质1中四个交点P,Q,S,T均不在y轴上,且在坐标变换(11)下分别变为P′,Q′,S′,T′,则由性质 2 可知:

符合性质1条件,设性质2中四个交点P,Q,S,T在坐标变换 (11)下分别变为P′,Q′,S′,T′,则由性质 1 可知:

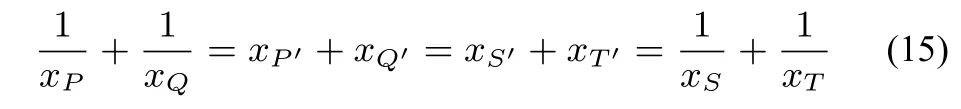
即性质2成立.