导数应用现难点 变式思维出奇招

广东省东莞市第一中学(523000) 孙传平

导数应用现难点 变式思维出奇招

广东省东莞市第一中学(523000) 孙传平

导数既是高考数学试题中的重点,也是难点,对以导数压轴的高考试题的求解运用常规思维往往显得很笨拙,甚至无能为力.文章归纳总结导数应用中的几种变式思维,对于突破难点、优化思维、提升能力大有裨益.

导数应用 变式思维

导数自编入高中数学课程以来,一直是高考数学的热点,在历年高考数学试题中不仅占有较大比重,而且常常以压轴题的地位出现,显现出导数应用难度加大的趋势有增无减,导致对其求解运用常规思维往往显得很笨拙,甚至无能为力.为此,本文介绍导数应用中的几种变式思维,供大家参考.

变式思维1主动讨论法

例1 (2007年全国卷)设函数f(x)=ex−e−x.

(1)略;

(2)若对所有x≥0都有f(x)≥ax,求a的取值范围.

解(2)记g(x)=f(x)−ax,则g′(x)=ex+e−x−a.因为ex+e−x≥2,所以

当a≤2 时,恒有g′(x)≥0(g′(x)不恒为零),这时函数g(x)在[0,+∞)上为增函数,于是g(x)≥g(0)=0,即恒有f(x)≥ax,符合题意;

综上所述,a的取值范围是(−∞,2].

点评第(2)问相当于“若函数g(x)≥0恒成立,求a的取值范围”.这种题型的常规思维,是通过解不等式[g(x)]min≥0,求得参数a的取值范围.但是上述求解并没有这样做,而是根据ex+e−x≥2,主动对参数a提出讨论,得到a≤2符合题意,a＞2不符合题意.象这种根据导函数中的某种信息,主动对参数a进行分类讨论,得到其取值范围的思维方法,在此归纳为“主动讨论法”.

变式思维2多次求导法

例2 (2010年全国卷)已知函数f(x)=(x+1)lnx−x+1.

(1)若xf′(x)≤x2+ax+1,求a的取值范围;

(2)证明:(x−1)f(x)≥0.

(1)的求解略;下面探讨(2)的证明.

视角1 (x−1)f(x)＞0等价于(x−1)与f(x)同号.

方法1 函数f(x)的定义域为(0,+∞).当x=1时,不等式显然成立;当x＞1时,所以f(x)在(1,+∞)上单调递增,于是f(x)＞f(1)=0,这时(x−1)f(x)＞0成立;当0＜x＜1时所以函数f′(x)在区间(0,1)上单调递减,从而f′(x)＞f′(1)=1＞0.所以f(x)在(0,1)上单调递增,故f(x)＜f(1)=0,这时(x−1)f(x)＞0成立.综上所述成立.

点评当0＜x＜1时,原本希望得到f(x)＜0,但由于f′(x)的符号难以确定,使求解遇到了麻烦,于是对f′(x)再次求导,目的是想通过f′′(x)来研究 (f′′(x)为f′(x)的导函数).象这种对导函数再次求导的思维方法在此归纳为“多次求导法”.

视角2 记h(x)=(x−1)f(x),则问题等价于x＞0时,

方法2 记

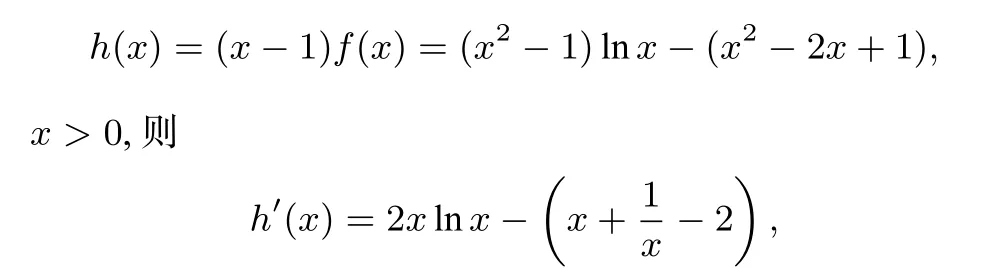
点评方法2关键在于摸清函数h(x)的单调性,但由于h′(x)与h′′(x)的符号都难以确定,故需要3次求导,借助h′′′(x)的信息逐步逆推(方法1与方法2思维起点低,思路清晰自然,不失为本题又一优秀解法).

变式思维3部分求导法

例3(2011年全国文21题)已知函数曲线y=f(x)在x=1处的切线为x+2y−3=0.

(1)求a,b的值;

一般地,若一个函数(或导函数)可以表示成两个因式的积,且其中一个因式的属性已明,另一个因式的属性未知,这时可将属性未知的因式单独揪出来求导,以此来研究原函数的属性.这种方法相当于从函数(或导函数)中分离出一部分来求导,在此将其归纳为“部分求导法”.

例4 (2013年辽宁理21)已知函数f(x)=(1+x)e−2x,当x∈[0,1]时,

(2)若f(x)≥g(x)恒成立,求a的取值范围.

解(2)由(1)知

当a+3≤0时,−xh(x)≥0,故f(x)−g(x)≥0,即f(x)≥g(x)恒成立;

当a+3＞0时,

综上所述,实数a的取值范围是(−∞,−3].

点评第(2)问有一定的难度,这里综合运用了部分求导法(记h(x),u(x))、多次求导法(对h(x)2次求导)、对a+3主动讨论等3种变式思维方法.

变式思维4以小拨大法

例5 已知函数其中e为自然常数.

(1)讨论f(x)的单调性与极值;

解(1)的求解略,下面先从两个角度给出(2)的求解.

点评方法1是处理“f(x)＞g(x)”最常规、最基本的思维,本题运用方法1颇有难度;倒是方法2,直接由不等式左边函数的最小值大于右边函数的最大值,轻轻松松获解,令人惊喜!在此将方法2的思维归纳为“以小拨大法”.

一般地,证明f(x)＞g(x)恒成立,常规思维是证明h(x)=f(x)−g(x)＞0恒成立.当常规思维受阻时,不妨换个视角,试试[f(x)]min＞[g(x)]max.显然当[f(x)]min＞[g(x)]max时,必有f(x)＞g(x)恒成立.

例6 (2014年新课标I理21)设函数f(x)=aexlnx+曲线y=f(x)在点(1,f(1))处的切线为y=e(x−1)+2.

(1)求a,b;

(2)证明:f(x)＞1.

点评第(2)问虽然解法不唯一,但是其它解法的难度都比较大,一般同学难以做到.这种情况下,若能及时调整思维视角,运用“以小拨大法”,则可使问题峰回路转、柳暗花明(若将第(2)问转化为后再运用该法亦可).

以上6例通过变换思维视角,使问题简捷获解,充分显示了这些变式思维在导数应用中的威力.数学解题既有普遍规律,也有其特殊性.我们学习数学解题既要知晓其常规思维,又要知晓其变式思维,只有这样,才能更有利于优化我们的思维,提升我们的能力;才能使我们在学习上立于不败之地.

链接习题

1.(2014年陕西理21(2))设函数f(x)=ln(1+x),g(x)=xf′(x),x≥0,f′(x)是f(x)的导函数.若f(x)≥ag(x)恒成立,求实数a的取值范围.

2.(2010年新课标)设函数f(x)=ex−1−x−ax2,若当x≥0时f(x)≥0,求a的取值范围.

3.(2007年安徽)设a≥0,f(x)=x−1−ln2x+2alnx.求证:当x＞1时,f(x)＞0恒成立.

链接习题提示