一类几何图形的问题设计
2017-08-07肇庆学院数学与统计学院526061邢志涛
肇庆学院数学与统计学院(526061) 邢志涛
一类几何图形的问题设计
肇庆学院数学与统计学院(526061) 邢志涛
对一类由三角形两边或者各边分别向外作正方形的这一类图形展开讨论,对相关的几何问题进行设计,揭示它们之间的联系.
几何图形 平面几何 问题设计
平面几何学科的特点是生动直观的图形和严谨的逻辑结构.图形是几何证明的一支有力拐杖,离开它,几何问题无从谈起[1].由一个三角形两边或者各边向外作正方形的这一类图形所涉及到的几何问题经常出现,并且问题之间密切联系.这类问题蕴涵了许多涉及到度量关系和位置关系的几何问题,融合了诸如作辅助线法、变换法、向量法等多种几何证明方法.对于这一类图形引起的问题进行设计,从简单到复杂的进行探索,揭示它们之间的联系,是本文的主要内容.
问题1. 如图1,分别以△ABC的边AB,AC为边,向外作正方形ABFG和ACDE,连接EG,求证:S△ABC=S△AEG.
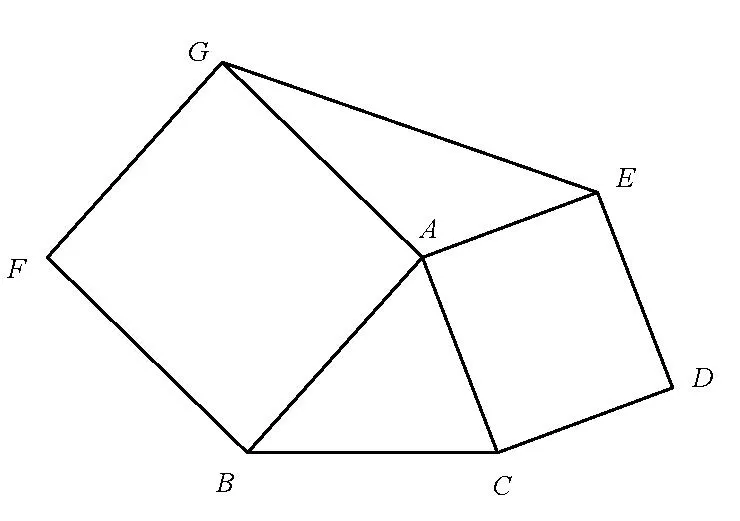
图1
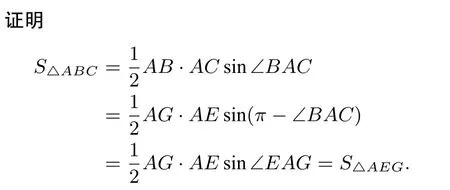
有了问题1作为基础,下面的问题就迎刃而解了.
问题2.如图2,分别以△ABC的边AB,AC,BC为边,向外作正方形ABDE,ACFG和BCHI,连接DE,EG,GF,FH,HI,ID.设AB=c,AC=b,BC=a,试用a,b,c来表示六边形DEGFHI的面积.
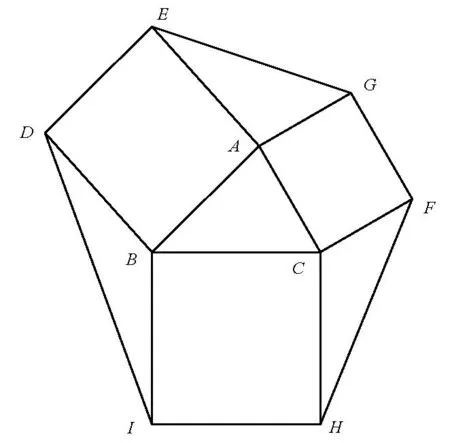
图2
解根据问题1,

问题3. 如图3,分别以△ABC的边AB,AC为边,向外作正方形ABFG和ACDE,连接EG.若O为EG的中点,求证:BC=2AO.
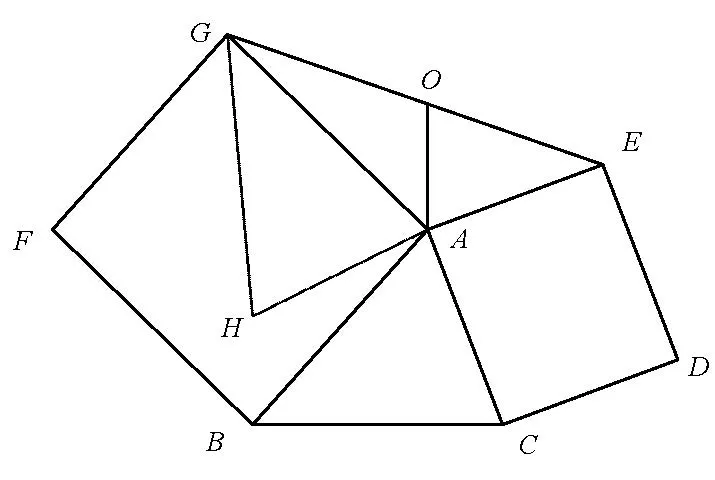
图3
证明延长EA到H,使得EA=AH,连接GH.显然OA是△EGH的中位线,则有GH=2OA.在△AGH和△ABC中,AG=AB,AH=AC,∠GAH= ∠BAC,所以△AGH∼=△ABC,从而GH=BC=2OA.
问题4. 如图4,分别以△ABC的边AB,AC为边,向外作正方形ABFG和ACDE,连接EG.若O为EG的中点,OA的延长线交BC于点H.求证:AH⊥BC.

图4
证明延长AO到I,使得AO=OI,连接GI与EI,则四边形AEIG为平行四边形.不难发现∠AGI=∠BAC.在△AGI和△BAC中,BA=AG,∠AGI= ∠BAC,AC=GI,则△AGI∼=△BAC,从而 ∠ABC= ∠GAI.由此,AH⊥BC.
问题5. 如图4,分别以△ABC的边AB,AC为边,向外作正方形ABFG和ACDE,连接EG.若AH⊥BC,HA的延长线交EG于点O.求证:O为EG的中点.
证明延长AO到I,使得AI=BC,连接GI与EI.根据AH⊥BC不难得到∠ABC= ∠GAI.在△AGI和△BAC中,AB=AG,∠ABC= ∠GAI,BC=AI.则△AGI∼=△BAC,从而 ∠BAC= ∠AGI,AE=AC=GI.由此,∠AGI+∠GAE=π,GI平行且等于AE,则四边形AEIG为平行四边形,O为EG的中点.
在上述三个问题的讨论中,虽然是不同的问题,但是解决的方法是一样的,就是通过引辅助线,得到与△ABC全等的三角形,进而解决问题.
问题6.如图5,分别以△ABC的边AB,AC为边,向外作正方形ABFG和ACDE,分别连接BE,CG相交于H.求证:BE=CG,BE⊥CG.
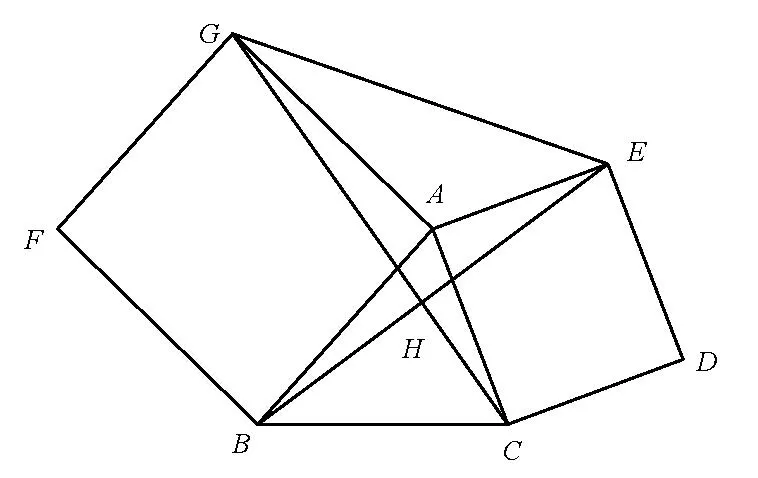
图5
证明在△ACG和△AEB中,AC=AE,∠GAC=∠BAE,AG=AB,所以△ACG∼=△AEB,从而BE=CG,∠ACG= ∠AEB.由此,在四边形EDCH中,∠HED+∠HCD=π,BE⊥CG.
问题7.如图6,分别以△ABC的边AB,AC为边,向外作正方形ABFG和ACDE,连接CE,BG,GE,M,N,P,G分别是EG,GB,BC,CE的中点.求证:四边形MNPQ是正方形.
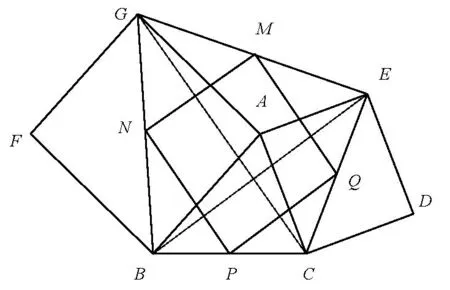
图6
证明分别连接BE,CG,根据问题6得:BE=CG,BE⊥CG.又已知M,N,P,Q分别是EG,GB,BC,CE的中点,所以MN平行且等于QP,MN=NP,MN⊥NP.由此,四边形MNPQ是正方形.
在上述两个问题的讨论中,正是有了问题6的解决,问题7能够比较顺利的得到解决.
问题8.如图7,分别以△ABC的边AB,AC为边,向外作正方形ABFG和ACDE,连接EG,作FM⊥BC交CB的延长线于点M,作DN⊥BC交BC的延长线与点N.求证:FM+DN=BC.

图7
证明过点A作AH⊥BC交BC于H.在Rt△FMB和Rt△BHA中,由于∠FBM=∠BAH,又有AB=BF,所以Rt△FMB∼=Rt△BHA,从而FM=BH. 同理Rt△DNC∼=Rt△CHA,从而DN=HC.综上得到FM+DN=BC.
问题9.如图8,分别以△ABC的边AB,AC为边,向外作正方形ABFG和ACDE,连接DF,O是DF的中点,OP⊥BC于BC上的点P.求证:BC=2OP.
证明根据问题8,FM+DN=BC.不难发现,OP是直角梯形DNMF的中位线,故有从而BC=2OP.
以上两个问题中,直接解决问题9是非常困难的,但是正是有了问题8的结论,问题9的解答就变得如此简单了.从这一点也可以看出,很多几何问题通过化繁为简,非常有助于问题的解决.接下来的问题10,也是可以通过上述两个问题的结论很容易得到解决.
问题10. 如图8,分别以△ABC的边AB,AC为边,向外作正方形ABFG和ACDE,连接DF,O是DF的中点,分别连接OB,OC.求证:OB=OC,OB⊥OC.
证明将上述两个问题所作的辅助线保留.根据问题8 的证明过程得,Rt△FMB∼=Rt△BHA,Rt△DNC∼=Rt△CHA,由此,CN=AH=BM,从而P也是BC的中点.再根据问题9的结论BC=2OP,这样就很容易的得到△BOC为等腰直角三角形,OB=OC,OB⊥OC.

图8
接下来介绍一个引理.
引理1[2]设R(O1,θ1),R(O2,θ2)是平面上两个具有不同旋转中心的旋转变换(这里R(O,θ)表示的是平面上以O为旋转中心,通常是逆时针旋转角θ的变换).若θ1+θ2≠2kπ,则R(O1,θ1) 与R(O2,θ2) 的复合变换R(O1,θ1)·R(O2,θ2)是一个旋转变换.设其旋转中心为O3,又有R(O1,θ1)·R(O2,θ2)=R(O3,θ1+θ2),同时

问题11[3]如图9,分别以△ABC的边AB,AC为边,向外作正方形ABFG和ACDE,连接EG.若AH⊥BC,连接BD,CF.求证:AH,BD,CF相交于一点.

图9
证明延长HA到I,使得AI=BC,则在△ABI与△BFC中,AI=BC,AB=BF,又不难得到∠BAI=∠FBC,所以△ABI∼=△BFC,∠BFC= ∠ABI. 而∠BFC+∠FBI= ∠ABI+∠FBI=所以CF⊥BI.同理可得:BD⊥CI.在△IBC中,AH,BD,CF分别是从三个顶点到对边的垂线,所以它们相交于一点,这一点是△IBC的垂心.
问题12 如图9,分别以△ABC的边AB,AC为边,向外作正方形ABFG和ACDE,连接EG,O为EG的中点.若BD,CF相交于一点K.求证:OA⊥BC,AK⊥BC.
证明根据问题4得到OA⊥BC.再根据问题11,点K是△IBC的垂心,所以AK⊥BC.

接下来的问题是问题6的简单变化.
问题13[4]如图10,设△ABO与△CDO是两个具有公共直角顶点的等腰直角三角形.求证:AC=BD,AC⊥BD.

图10
而下面的问题则是问题7的特殊情形.
问题14[4]如图11,分别以△ABC的边AB、AC为边,向外作正方形ABFG和ACDE,P,Q分别是正方形ABFG和ACDE的中心.求证:若M是BC的中点,则△PMQ是等腰直角三角形.
有兴趣的读者不妨试着通过几何变换的方法从问题13来推导问题14.
通过上述问题的分析发现,几何问题的联系是非常密切相关的.将问题逐步简化,由简入繁,是解决几何问题一个非常有效的途径.
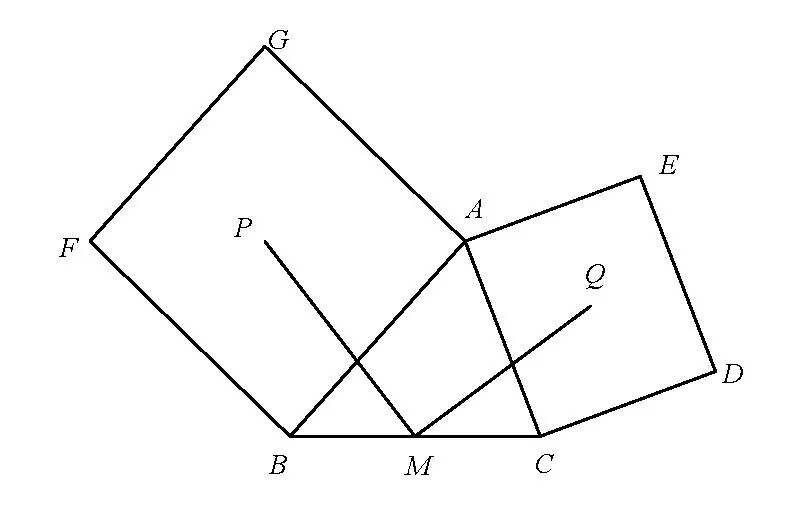
图11
[1]王家铧,沈文选.几何课程研究[M].北京:科学出版社,2006.
[2]席高文,许梦日.中学几何研究与教学[M].郑州:郑州大学出版社,2007.
[3]刘俊,付本路,姚玉平.初等数学解题方法教学研究[M].东营:石油大学出版社,2009.
[4]爱德华.J.巴尔博等著,王继延等译.给数学迷的500个挑战性问题[M].上海:上海科技教育出版社,2007.
