一类绝对值函数最值的求法

北京丰台二中(100071) 甘志国

一类绝对值函数最值的求法

北京丰台二中(100071) 甘志国

我们先看看两个例题:

例1 求函数y=|x−1|+2|x−2|+···+100|x−100|(x∈R)的最小值.

解先将原函数写成1+2+···+100=5050个绝对值之和的形式,再首尾配对,层层分组,得

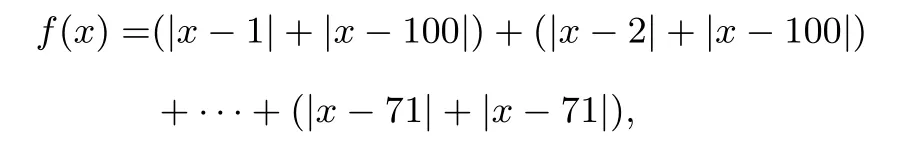
当且仅当x∈[1,100]时,以上等式右边第一个括号取到最小值;当且仅当x∈[2,100]时,以上等式右边第二个括号取到最小值;···;当且仅当x=71时,以上等式右边最后一个括号取到最小值.所以,当且仅当x=71时,f(x)取到最小值.可算得最小值是99080.

定理1 若函数

所以,当且仅当x∈[bk0,bk0+1]时,f(x)取到最小值.

推论1 若函数

(1)当n为奇数时,当且仅当时,f(x)取到最小值;

(2)当n为偶数时,当且仅当时,f(x)取到最小值.

例1 (1)(2014年高考江西卷理科第11(1)题)对任意x,y∈R,|x−1|+|x|+|y−1|+|y+1|的最小值为( )

A.1 B.2 C.3 D.4

(2)(2014年高考江西卷文科第15题)x,y∈R,若|x|+|y|+|x−1|+|y−1|≤2,则x+y的取值范围为____.

解(1)C.由推论1(1)可得,当且仅当x∈[0,1]时,(|x|+|x−1|)min= 1;当且仅当y∈[−1,1]时,(|y+1|+|y−1|)min=2.所以所求最小值为3.

(2)[0,2].由推论1(1)可得,当且仅当x∈[0,1]时,(|x|+|x−1|)min=1;当且仅当y∈[0,1]时,(|y|+|y−1|)min=1.所以(|x|+|y|+|x−1|+|y−1|)min=2.再由题设|x|+|y|+|x−1|+|y−1|≤2,可得|x|+|y|+|x−1|+|y−1|=2,且x∈[0,1],y∈[0,1].进而可得x+y的取值范围为[0,2].

例2 (2006年高考全国卷II理科第12题)函数的最小值为( )

A.190 B.171 C.90 D.45

解C.由推论1(1)可得,当且仅当x=10时,f(x)取到最小值,且最小值是2(1+2+···+9)=90.

例3(1)(2009上海高考文科第14题)某地街道呈现东—西、南—北向的网络状,相邻街距都为1,两街道相交的点称为格点.若以相互垂直的两条街道为轴建立直角坐标系,现有下述格点(−2,2),(3,1),(3,4),(−2,3),(4,5)为报刊零售店,请确定一个格点____为发行站,使5个零售点沿街道发行站之间路程的和最短;

(2)(2009上海高考理科第13题)某地街道呈现东—西、南—北向的网格状,相邻街距都为1.两街道相交的点称为格点.若以互相垂直的两条街道为轴建立直角坐标系,现有下述格点 (−2,2),(3,1),(3,4),(4,5),(−2,3),(6,6),为报刊零售点.请确定一个格点(除零售点外)____为发行站,使6个零售点沿街道到发行站之间路程的和最短.

解(1)(3,3).设所求的格点坐标为(x,y)(x,y∈Z),则它到5个零售点沿街道发行站之间路程的和为

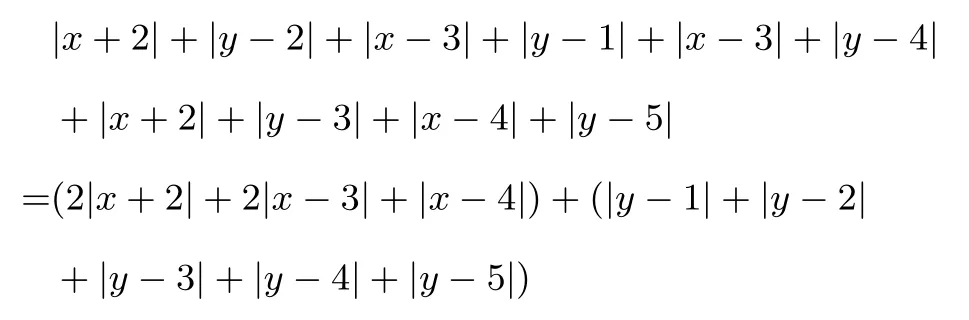
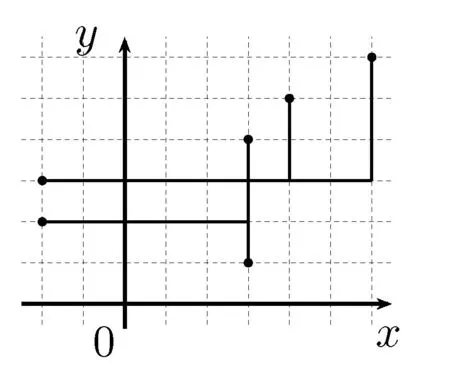
图1

再由定理1(1)可得答案.(2)(3,3).设所求的格点坐标为

(x,y)(x,y∈Z,则它到6个零售点沿街道发行站之间路程的和为

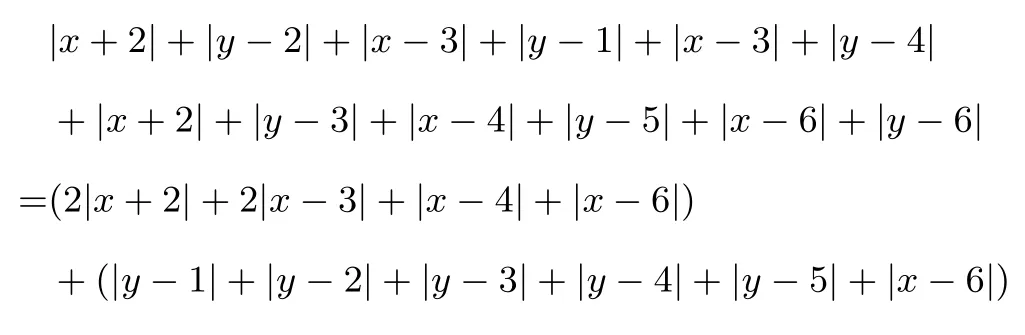
再由定理1(1)可得答案(如图1所示).

例4 (2011年北约自主招生数学试题第7题)求f(x)=|x−1|+|2x−1|+···+|2011x−1|(x∈R)的最小值.

定理2 对于函数

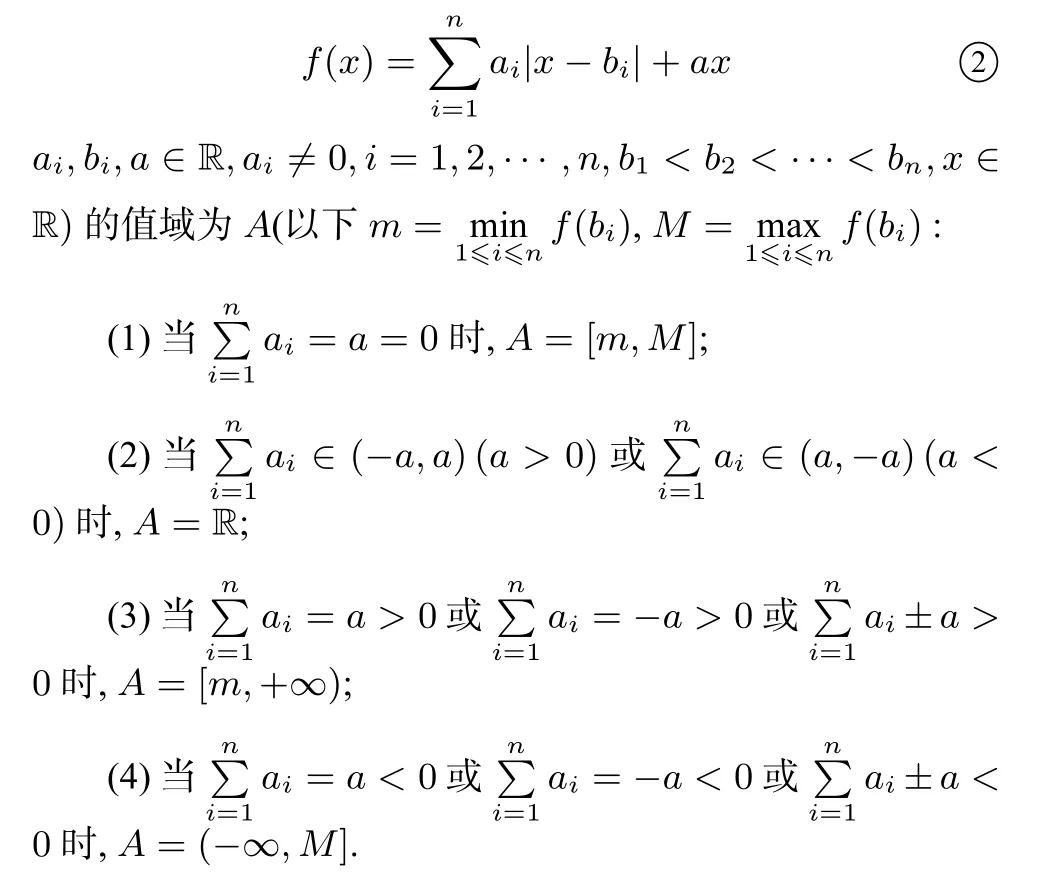
证明因为函数②在分段点b1,b2,···,bn处均连续,所以可把函数②改写成如下分段函数:

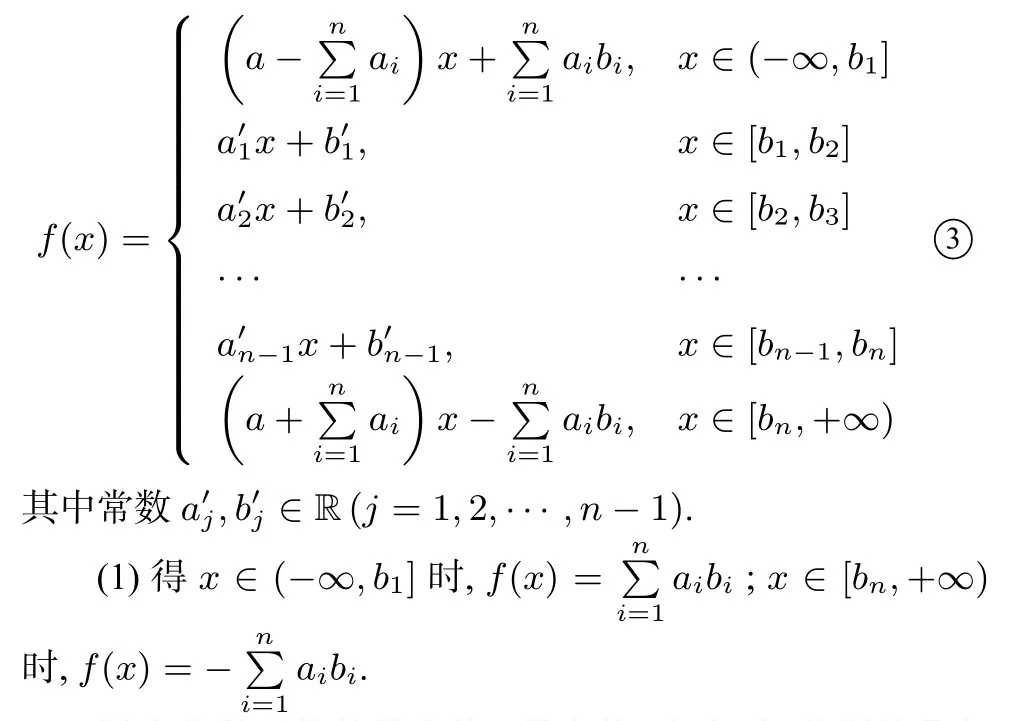
因为分段函数的最小值、最大值(存在时)分别就是各段函数最小值、最大值(存在时)中的最小、最大者,又③中各段函数都是闭区间上的一次函数或常数函数,其最小值、最大值一定是某个端点的函数值,所以函数②的最小值、最大值分别为

再由函数②在R上连续,可立得函数②的值域是[m,M].

(4)同(3)可证.在定理2中,令a=0,可得

推论2 对于函数

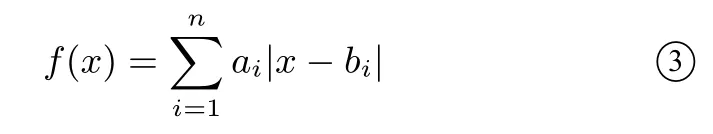
例5 求函数f(x)=|x|−|x−1|−|x−2|+|x−3|(x∈R)的值域.

解f(0)=1,f(1)=f(2)=2,f(3)=0.由推论2(3),得[f(x)]min=min{f(0),f(1),f(2),f(3)}=0;[f(x)]max=max{f(0),f(1),f(2),f(3)}=2..再由函数f(x)的连续性可画出f(x)的图象,从而得当且仅当x≥3时,f(x)取到最小值;当且仅当1≤x≤2时,f(x)取到最大值.

定理3设(α＞1,b1,b2,···,bn是公差为的实数项等差数列),则函数f(x)的值域是[A,+∞),且有:

证明若d=0,要证结论显然成立.下证d＞0时也成立,得b1＜b2＜···＜bn.可先用导数证得:设g(x)=xα(a＞1,x＞0),则g(x)是增函数;且g′′(x)＞0,所以g(x)是下凸函数,得

(2)同(1)可证.