邻域自适应增量式PCA-LPP在齿轮箱故障诊断中的应用
2017-07-19邓士杰唐力伟张晓涛
邓士杰, 唐力伟, 张晓涛
(军械工程学院 火炮工程系, 石家庄 050003)
邻域自适应增量式PCA-LPP在齿轮箱故障诊断中的应用
邓士杰, 唐力伟, 张晓涛
(军械工程学院 火炮工程系, 石家庄 050003)
针对流形学习算法的增量处理问题,提出一种邻域自适应增量式PCA-LPP流形学习算法,阐述了算法的基本原理以及增量样本处理方法。对新增样本的引入,首先根据已有样本对协方差矩阵和相似矩阵进行增量更新,而后结合已有样本降维结果对新增样本降维结果进行估计,最后采用子空间迭代法实现新旧样本降维结果的更新。采用齿轮箱故障信号特征向量对邻域自适应增量式PCA-LPP流形学习算法进行检验,结果表明,邻域自适应增量式PCA-LPP流形学习算法降维后特征具有良好的故障分类识别效果。
增量式学习;自适应;流形学习;故障诊断
流形学习是一类有效的非监督数据降维方法[1-2],能够提取嵌入在高维数据中的低维特征,为后续的数据分类提供有效的特征降维处理支持。He等[3]在拉普拉斯映射的基础上,提出一种典型的局部保持投影算法(Locality Preserving Projection, LPP),其能够在投影过程中保持数据样本局部流形结构不变,并将其应用于人脸识别研究。主元分析PCA在降维时具有考虑样本全局结构的特性,而LPP则具有保持数据样本局部流形结构的特性,综合PCA与LPP特点,可以实现在降维过程中数据样本局部和全局结构特征协同保持的目标。文献[4-6]进行了PCA与LPP联合的方法在图像重构、故障检测及特征增强的相关研究,并且流形学习方滚动轴承故障信号特征的降维识别中目前已有广泛应用[7],为滚动轴承故障诊断提供了新的处理思路和方法。
传统的典型流形学习算法均是批量式处理,一旦有新样本增加时,需要对新旧所有样本全部进行处理,这样的处理方法往往计算量大,耗时耗力,并且已有样本的降维结果得不到有效利用。近些年来,众多学者对增量流形学习算法进行了研究,主体上分为两类。一是利用已有样本的降维结果对新增样本的降维结果进行估计,如Jia等[8]基于拉普拉斯映射图像识别所进行的增量式学习研究,以及Chin等[9]针对最大方差投影MVU所进行的增量式学习研究。二是在已有样本降维结果的基础上,引入新增样本,采用迭代方法同时更新所有样本的投影结果,从而得到最终的降维结果。如杨庆等[7]对增量式局部切空间排列算法及其在故障诊断中所作的研究,以及谈超等[10]基于等角映射的多样本增量流形学习算法及其在人脸识别中的研究。
文中针对PCA与LPP算法,引入邻域自适应构造方法,对算法求解目标函数进行改写,提出一种邻域自适应增量式PCA-LPP流形学习算法。该算法能够利用已有样本的降维结果,对新增样本通过求解矩阵方程,得到投影结果的初始估计,而后采用Rayleigh-Ritz加速子空间迭代法,同步更新已有样本和新增样本的投影结果,最终得到所有样本的低维投影结果。文中所提方法主要是在LPP算法基础上引进了迭代更新的处理方法,能够得到准确的降维结果,避免利用已有降维结果估计新样本降维结果得到的估计值。最后针对齿轮箱故障声发射信号特征向量对其进行检验,结果表明,文中方法降维处理后,故障识别率得到有效提升。
1 PCA-LPP流形学习算法
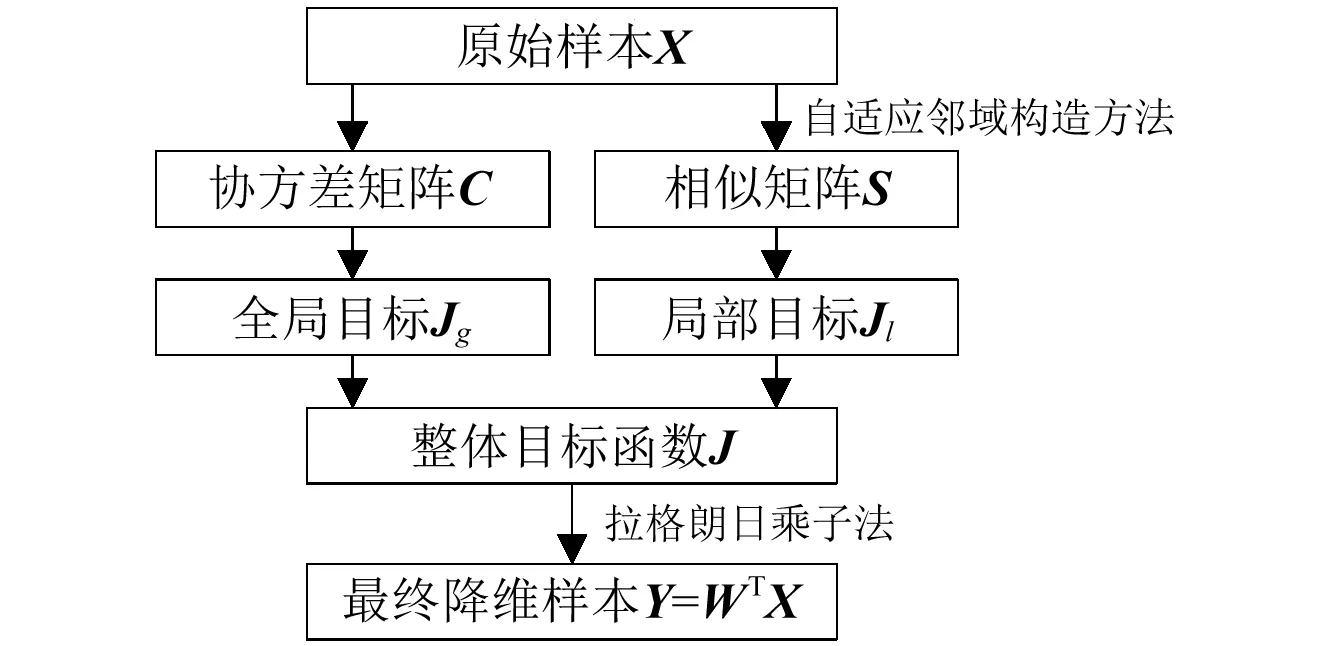
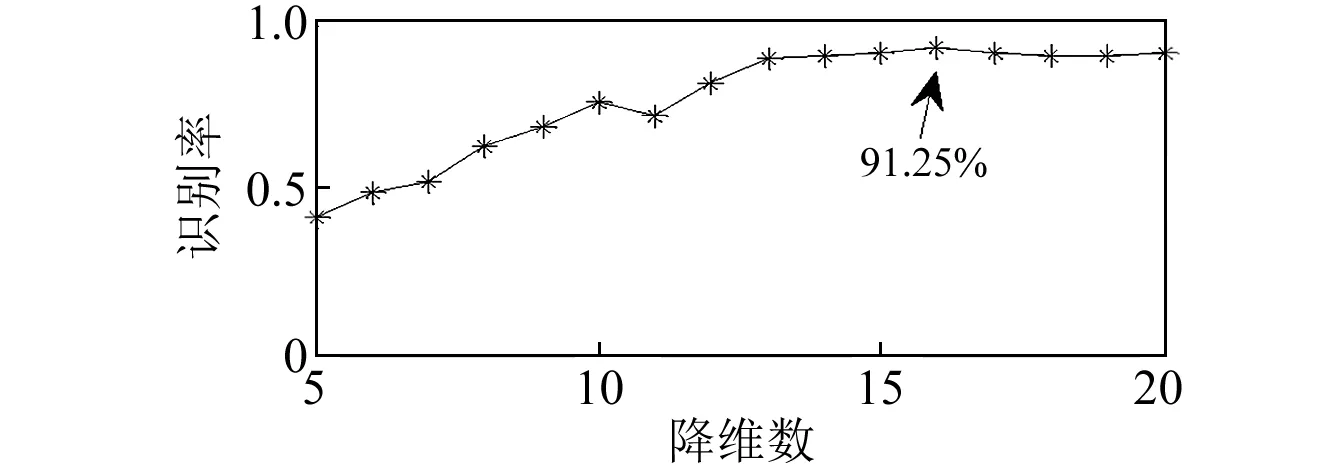
PCA-LPP流形学习算法结合PCA数据整体分布描述及LPP数据局部流形信息描述,构造整体的投影矩阵求解方程。设在高维空间RD中存在数据集x=[x1,x2,…,xN],共包含N个数据样本。PCA-LPP流形学习算法的目标是寻找投影变换矩阵W,将X转换投影为空间Rd(d PCA-LPP流形学习算法的整体目标函数基于全局目标函数Jg和局部目标函数Jl构造,从而使整体目标函数求解的投影矩阵能够同时兼顾PCA与LPP的特性。 1.1 全局目标函数 全局目标函数Jg即为PCA投影,能够使投影后数据在低维空间保持原始样本的大部分方差信息,其表达式如式(1)所示,式中C为协方差矩阵。 (1) 1.2 局部目标函数 局部目标函数Jl即为局部保持投影LPP,其能够使投影前后数据局部近邻结构相似,其表达式如式(2)所示。 (2) 样本间马氏距离dij计算如式(3)所示,基于马氏距离的样本间相似系数αij计算及初始近邻确定如式(4)所示。 (3) (4) 得到样本初始近邻数后,基于高斯核密度估计[11](Gauss Kernel Density Estimation,GKDE)方法计算样本点的总体分布概率密度。对样本xi来讲,其分布概率密度愈大,表明与其具有相似局部特征的样本越多,该样本的近邻数应该愈大。样本xi的邻域概率密度高斯核估计,如式(5)所示。 (5) (6) 式中,floor表示数据向负无穷大方向取整。根据最终确定的近邻数计算相似系数得到相似矩阵S。自适应邻域方法计算得到的各个样本近邻数一般不相等,因此相似矩阵S一般不是对称矩阵,但拉普拉斯矩阵L是对称矩阵,因为矩阵D′与S′是对称矩阵,所以L=D′-S′是对称矩阵。 1.3 整体目标函数 结合全局目标函数与局部目标函数,构造整体目标函数如式(7)所示。 (7) 将Y=WTX代入其中,可得式(8),并根据式(8)直接求解投影结果Y。 (8) 整体目标函数可以通过拉格朗日乘子法转换为有约束最大值问题,如下 (9) 式(9)对Y求导并置零可得: (10) 式(10)化简后得到式(11),投影矩阵W的求解实质上是求解广义特征值问题,通过求解前d个最大特征值对应的特征向量,得到投影矩阵W。 (11) 根据邻域自适应构造方法以及整体目标函数,可以给出邻域自适应PCA-LPP流形学习算法的基本流程,如图1所示。 图1 邻域自适应PCA-LPP算法流程Fig.1 The flow of adaptive neighborhood PCA-LPP algorithm 邻域自适应PCA-LPP流形学习算法是一种批量式数据处理方法,不具备增量处理能力。处理新增样本时只能考虑所有样本重新计算投影矩阵,原始样本的投影结果不能得到有效利用,特别是在原始样本数量较大的情况下,每次重新计算整体的特征向量时计算量大,效率低。基于对自适应邻域PCA-LPP流形学习算法的分析,考虑对大量原始样本已有处理结果的应用,提出一种具有批量处理能力的增量式邻域自适应PCA-LPP流形学习算法。 2.1 相关参量矩阵更新 在原始分析数据集X的基础上,假设新增L个样本,新旧样本构成当前数据集,则此时的数据集Xnew=[x1,x2,…,xN,…,xN+L],共N+L个样本。加入新样本之后,算法整体目标函数计算过程中的参量均发生变化,如样本协方差矩阵C,目标函数中的相似矩阵S以及对角矩阵D。 增加新样本后首先需要更新整体协方差矩阵,协方差矩阵增量更新方法如式12所示[12]。 (12) (13) 在增量式整体目标函数中,原有批量式处理方法求解计算量大,且不能有效利用已有的样本降维结果。下面根据整体目标函数的特点,首先给出样本降维后的估计值,而后通过迭代法得到精确结果,这样处理能够有效利用已有数据的降维结果,降低运算量,并且在处理过程中同步更新已有样本的降维结果,实现增量式处理。 2.2 新样本嵌入坐标估计 (14) 原始数据集X∈RD投影到低维空间的结果为Y0∈Rd,假设增加新样本后的数据集Xnew∈RD投影到低维空间的结果为Ynew∈Rd,由于数据集样本数前后发生变化,可知Y0的样本数为N,而Ynew的样本数为N+L。 为了给出Ynew一个合理的估计值,按照原始样本数和新增样本数对式(14)进行分块构造,如式(15)所示。 (15) 将F=DT代入式(15)并展开可以得到式(16)。 (16) 上式对Y1求导并置零可得式(17)。 (17) 通过求解矩阵方程可以得到Y1的初始估计值,从而结合Y0组成Ynew的估计值。 2.3 投影结果迭代更新 式(14)中,Ynew的求解方程依然可以采用拉格朗日乘子法转换为有约束最大值问题,而后求导置零,从而可得式(18)。 (18) 从上式中可知,Ynew实际上是一个广义特征值问题,新样本加入后的特征值求解则是一个矩阵增量特征值问题。 采用Rayleigh-Ritz加速子空间迭代法,基于Ynew的估计值[Y0,Y1],通过迭代运算实现新旧样本投影结果的同时更新,Rayleigh-Ritz加速子空间迭代法计算流程如下。 (3) fori=1,2,……,k end 在迭代法计算过程中,步骤3.3需要求解一个Rd×d的广义特征值分解问题,由于d较小,因此特征值分解的计算量不大。经过迭代收敛后,可以实现投影结果中Y0和Y1的同时更新,从而得到在新邻域关系中的数据降维结果。根据前述算法的相关理论分析,可以得到增量式邻域自适应PCA-LPP流形学习算法流程如图2所示。 图2 增量式邻域自适应PCA-LPP算法流程Fig.2 Adaptive neighborhood incremental PCA-LPP algorithm 3.1 实验数据及特征提取 以二级减速箱实验平台为实验验证对象,输入轴齿轮齿数z1=25,中间轴大齿轮齿数z2=50,中间轴小齿轮齿数z3=19,输出轴齿轮齿数z4=81,中间轴滚动轴承型号为6206。采用线切割在中间轴齿数为50的齿轮以及轴承内外圈加工细小裂纹作为故障,线切割裂纹深度为1 mm,宽度为0.5 mm。 实验中振动加速度传感器型号为B&K4508,固定在齿轮箱故障轴承所在轴承座上,信号采集时,采样频率10 kHz,实验中输入轴转速1 500 r/min。 实验中共设置四种故障模式,分别为正常状态,齿根裂纹故障,轴承内圈裂纹故障,轴承外圈裂纹故障。实验中每类故障状态采集100个样本,四类故障类型共400个样本,每个样本信号时间长度为1 s。 针对实验信号,提取10个时域特征参数和10个频域特征参数构建20维故障特征向量,如表1所示。通过以上征参数的组合来全面准确地描述旋转机械不同部位、不同类型、不同程度故障的特征信息。其中,xi是时域信号序列,n=1,2,…,N,N为样本数量。sk是信号的频谱,k=1,2,…,K,K为谱线数,xi是第k条谱线的频率值。 表1 故障样本的特征参数 3.2 故障特征的降维识别 采用邻域自适应增量式PCA-LPP流形学习算法对故障特征进行降维处理。并结合支持向量机对故障特征进行分类识别,采用径向基核函数支持向量机,基于交叉验证方法获得核函数参数γ=2.7,惩罚因子c=1.2。 采用其中60%作为训练样本,剩余40%作为测试样本,给出降维数和故障分类识别率的关系曲线如图2所示。 图2 故障分类识别率曲线Fig.2 The curve of fault identification rate 从图2中的曲线可以看出,在降维数为16时,故障分类识别率最高,并且随着降维数的增加,故障识别率快速增大,且在降维数大于13后,故障识别率处于较为平稳的阶段。 3.3 不同降维方法识别性能的对比 采用PCA和LPP方法和文中的邻域自适应PCA-LPP方法的性能进行对比,同时在识别过结果中加入原始故障特征的识别情况。对比结果如表2所示。其中PCA和LPP及文中的邻域自适应增量式PCA-LPP方法的降维数均选为16。其中LPP方法采用k近邻方法选择邻域,经过多次验证设置k=9时故障识别率最高,表中故障识别率为测试样本中识别正确的个数与测试样本总数的比值。 表2 不同方法识别率对比 从表2中的结果可以看到,采用邻域自适应PCA-LPP流形学习算法进行特征降维后,故障特征的识别效果最好,其识别率高于PCA和LPP方法降维特征及原始故障在特征的故障分类识别效果。这主要是由于PCA和LPP的降维过程仅是单一的强调故障特征的整体结构方差和局部流形结构,原始的高维故障特征则存在不同故障特征之间的冗余信息,而PCA-LPP流形学习方法则能同时兼顾整体结构方差和局部流形结构。故此其降维后的故障特征能更好的反映不同故障之间的差异,获得更好的故障分类识别情况。 文中提出一种邻域自适应增量式PCA-LPP算法,该方法能够利用已有观测样本得到的协方差矩阵C和相似矩阵S以及新的低维投影结果,建立增量数据样本与其低维投影结果之间的关系,并通过迭代方法更新所有样本的低维投影结果。基于齿轮箱预置故障信号特征的处理实例表明,文中所提方法具有良好的故障特征降维效果,其降维后的特征故障分类识别率明高于PCA、LPP及原始故障特的分类识别率,说明PCA-LPP流形学习算法能够兼顾特征样本的整体方法差和局部流形特征,并能有效降低原始故障特征所存在的冗余信息。 [10] LIU H, XIANG C, FU S. Research on dynamic coupled characteristics of a tracked vehicle gearbox [J]. International Journal of Computational Intelligence Systems, 2011, 4(6): 1204-1215. [11] YI G, TUGAN E, TRISTAN M E, et al. Vibro-acoustic propagation of gear dynamics in a gear-bearing-housing system [J]. Journal of Sound and Vibration, 2014, 333: 5762-5785. [12] 高维金, 王亮, 刘永光. 箱式动力结构的振动传递特性分析 [J]. 北京航空航天大学学报, 2015, 41(3): 509-516. GAO Weijin, WANG Liang, LIU Yongguang. Analysis on vibration transmission characteristics of box-like power structure [J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(3): 509-516. [13] CHANG Lehao, LIU Geng, WU Liyan. A robust model for determining the mesh stiffness of cylindrical gears [J]. Mechanism and Machine Theory, 2015, 87: 93-114. Gear fault diagnosis based on an adaptive neighborhood incremental PCA-LPP manifold learning algorithm DENG Shijie, TANG Liwei, ZHANG Xiaotao (First Department, Ordnance Engineering College, Shijiazhuang 050003, China) Aiming at the incremental processing in manifold learning algorithms, an adaptive neighborhood incremental PCA-LPP manifold learning algorithm was presented. The incremental learning principle of the algorithm was introduced. For introducing the incremental sample data, the adjacency and covariance matrices were updated according to the incremental by using the existing sample. Then, the dimension reduction result of the incremental sample was estimated based on the dimension reduction result of the existing sample and updated matrix. Finally, the dimension reduction results of incremental and existing samples were updated by using the subspace iteration method. The adaptive neighborhood incremental PCA-LPP manifold learning algorithm was applied in the processing of gearbox fault signals. The dimension reduction results by the incremental learning are of very small error compared with the batch learning. The spatial aggregation of incremental samples is basically stable, and the fault identification rate is improved. incremental learning; adaptive; manifold learning; fault diagnosis 国家自然科学基金资助项目(50775219);军队科研资助项目 2016-06-15 修改稿收到日期: 2016-09-23 邓士杰 男,博士生,讲师,1983年生 唐力伟 男,教授,博士生导师,1961年生 TH165;TN911.3 A 10.13465/j.cnki.jvs.2017.14.017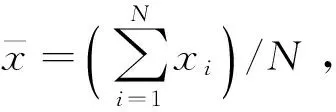
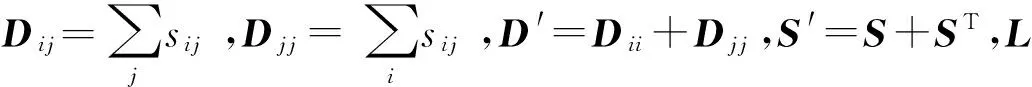
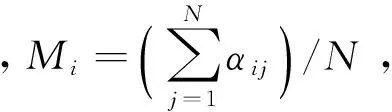

2 增量式PCA-LPP流形学习算法
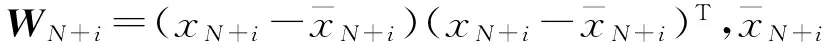
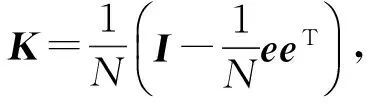
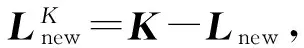
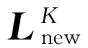

3 齿轮箱故障信号降维及识别分类


4 结 论
