FSWT-SVD模型在岩体微震信号特征提取中的应用

尚雪义， 李夕兵， 彭 康， 王泽伟， 翁 磊

(1. 中南大学 资源与安全工程学院，长沙 410083；2. 重庆大学 煤矿灾害动力学与控制国家重点实验室，重庆 400044； 3. 重庆大学 资源及环境科学学院，重庆 400044)

FSWT-SVD模型在岩体微震信号特征提取中的应用

尚雪义1， 李夕兵1， 彭 康2,3， 王泽伟1， 翁 磊1

(1. 中南大学 资源与安全工程学院，长沙 410083；2. 重庆大学 煤矿灾害动力学与控制国家重点实验室，重庆 400044； 3. 重庆大学 资源及环境科学学院，重庆 400044)

针对岩体破裂信号与爆破振动信号难以识别的问题，采用傅里叶变换(FT)得到其频谱分布，并确定划分为6个频带提取信号特征。借助频率切片小波变换(FSWT)将信号按上述频带切片并重构，再利用奇异值分解(SVD)得到上述频带重构信号所组成矩阵的奇异值σi(i=1,2,…,6),实现岩体微震信号的特征提取。进而对用沙坝矿120个岩体破裂和120个爆破振动信号展开FSWT-SVD分析，最后利用BP神经网络对奇异值矩阵进行分类训练和预测。结果表明：①岩体破裂信号与爆破振动信号的奇异值σ1相差最大，σ2、σ4、σ5和σ6相差较大，而σ3差异不明显，且当σ1=8作为单一奇异值法识别分界值时效果最优，准确率达到了86.67%；②BP神经网络法分类识别结果较LR法、Bayes法和Fisher法优，SVD提取特征识别效果较能量比和相关系数优，FSWT重构矩阵提取的特征信息优于DWT重构矩阵提取的特征信息，且基于FSWT-SVD的BP法分类识别准确率达到了91%。综上知，基于FSWT-SVD的BP神经网络模型为岩体破裂与爆破信号特征提取和模式识别提供了一种新方法。

岩体微震信号；频率切片小波变换；奇异值分解；特征提取；模式识别

岩体微震信号的识别对微震监测具有重要意义[1]，常见的岩体微震信号有岩体破裂信号、爆破振动信号、凿岩冲击信号、溜井放矿信号、铲运机作业信号和风机振动信号等。其中大多数岩体微震信号很容易排除，而岩体破裂信号与爆破振动信号相似性较大，且常受众多噪音信号干扰，识别非常困难[2-3]。为简化说明，下文中的岩体微震信号均专指岩体破裂信号和爆破振动信号。目前，主要采用人工识别岩体破裂信号和爆破振动信号，但人工识别的效率低下，且易受个人因素影响。由此，如何有效自动识别岩体破裂信号和爆破振动信号仍是当下面临的一个重大问题[4]。

目前，识别岩体破裂信号和爆破振动信号的方法可分为波形时频分析、振幅峰值比分析和机器学习法[5]。其中，时频分析作为一种有效的波形特征提取手段，在岩体微震信号识别中得到了广泛的应用。岩体微震信号的时频识别方法主要是基于傅里叶变换(Fourier Transform, FT)[6-8]、小波变换(Wavelet Transform, WT)[9]、小波包变换(Wavelet Packet Transform, WPT)[10]和希尔伯特-黄变换(Hilbert-Huang Transform, HHT)[11-12]等。

傅里叶变换可完成信号从时域到频域的转换，也可完成信号从频域到时域的转换，但其不能同时具有时域和频域信息，且傅里叶分析不能描述信号的局部特征；小波和小波包分析具有较好的时频分辨率，对非平稳信号的时频特征分析和提取具有良好的自适应性，但如何选取小波基和分解尺度是应用中的难题，且其将信号按尺度固定频段分解，每一频段只与信号的采样频率有关，而与信号本身信息无关，很容易受到信号中相邻谐波成分的交叠影响[13]。HHT法从信号自身局部特征出发进行自适应的时频分解，是一种更有效的时频局部化分析方法，且适用于非线性非平稳信号的分析[14]，但其存在频率混淆、端点效应明显等问题，降低了信号的保真度，分解过程中使用3次样条插值也增大了计算量。

Yan等[15-17]提出了一种新的时频分析方法—频率切片小波变换(Frequency Slice Wavelet Transform，FSWT)，通过引入频率切片函数使传统的傅里叶变换具有了时频分析功能，克服了小波和小波包变换依赖小波函数重构信号的缺陷，可实现信号任意频带的重构及局部特征的精确描述，并在信号处理领域得到了广泛应用[18-21]。奇异值分解(Singular Value Decomposition，SVD)能有效降低矩阵数据维数、提取矩阵特征，其与多尺度结合得到了许多特征提取模型，如EMD-SVD[22-25]、EEMD-SVD[26-28]、LMD-SVD[29-30]和小波-SVD[31-32]等，并取得了较好的分类效果。鉴于此，本文尝试利用傅里叶变换得到岩体微震信号的频谱特征，在此基础上采用FSWT对其进行频带切片和重构，再利用SVD提取FSWT频带重构信号所组成矩阵的奇异值，进而对岩体破裂信号与爆破振动信号的奇异值进行分析，以期得到一种新的岩体微震信号特征提取及分类识别方法。

1 岩体微震信号的FSWT-SVD研究

1.1 FSWT理论

1.1.1 频率切片小波变换

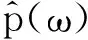
(1)

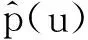
借助Parseval方程将式(1)转换到时域：

(2)

1.1.2 尺度因子的选择

不失一般性，令λ=1，根据Morlet小波变换原理，取σ∝ω，设尺度因子σ=ω/κ，并假定κ>0，则式(1)可变为

(3)

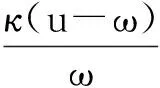
(4)

Heisenberg不确定性原理表明不可能同时在时域和频域得到高分辨率，因此需对时频分辨率采用折中分析，为此引入两个评价系数，一是频率分辨比率η：

(5)

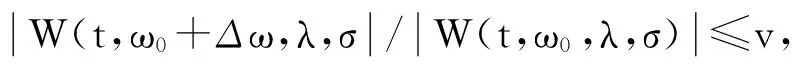
(6)

即：

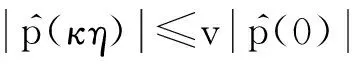
(7)

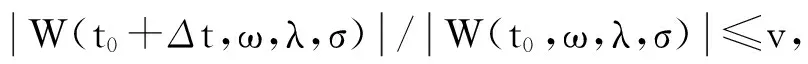
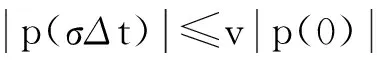
(8)

即：

(9)

式中：μ=ΔωΔt。

(10)

(11)

1.1.3 频率切片小波变换的逆变换

FSWT的时频分解结果是冗余的，可采用不同形式的逆变换重构原始信号，其中一种最简单的逆变换表示为：

(12)

式(12)表明其逆变换只与κ有关，与函数p(ω)无关，当κ给定时，式(12)为傅里叶逆变换。

若信号f(t)的FSWT变换为W(τ,ω,κ)，则在时频区域(t1,t2,ω1,ω2)的信号分量为

(13)

由此知，在f(t)的FSWT时频区间内，可任意选取时频区域(t1,t2,ω1,ω2)，即FSWT可实现自由地在时频空间上提取所需的信号分量。

1.2 奇异值分解

SVD作为一种正交化的矩阵分解方法，在矩阵数据降维和特征提取中得到了广泛应用。假定信号FSWT重构频带数为m，采样点数为n，由此构造m×n阶矩阵X，其元素为xij(i为重构频带号，j为采样点号)，于是有：

(14)

根据SVD理论[33-34]，矩阵X可分解为：

X=USVT

(15)

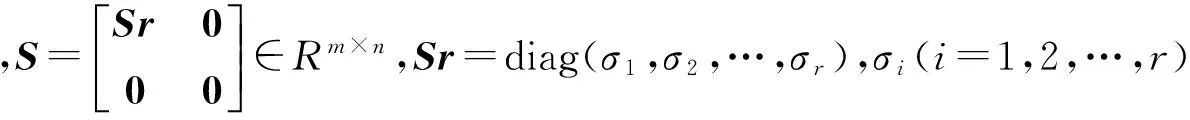
奇异值能有效地反映矩阵X的本质特征，当矩阵相似性较大时，奇异值稳定性较好。由此，奇异值可作为岩体破裂信号与爆破振动信号的特征值。此外，奇异值作为特征值降低了矩阵的维数，便于开展岩体微震信号识别的研究。

1.3FSWT-SVD特征提取方法

FSWT重构信号既保留了信号的局部特征，又能精确地给出不同频带信号与时间的联合分布情况。但FSWT在对信号不同频带信息描述的同时，数据量大大增加。为此，本文借助SVD对FSWT重构频带信号所组成矩阵进行维数压缩和特征提取，即奇异值矩阵为各频带信息的浓缩和重构信号的特征向量。

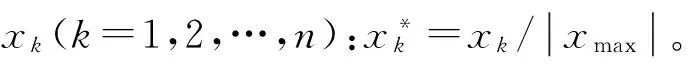
2 岩体微震信号的FSWT-SVD特征分析

为对岩体微震信号进行有效的分类，本文使用开阳磷矿用沙坝矿IMS微震监测信号作为分析的基础。该系统示意图如图1所示，其包含1个井上微震服务器、1个井下数据交换中心、4个主台站、4个副台站、2只三分量传感器和26只单分量传感器。单、三分量传感器与台站分别用4芯和6芯信号电缆连接，副台站与主台站采用4芯光纤连接，主台站与数据中心采用6芯光纤连接。传感器采样频率均为6 000 Hz，且布置在930、1 080和1 120三个分层巷道内，可满足矿山的区域监测。但受噪音信号的干扰，岩体微震信号的自动识别准确率低，目前仍主要采用人工处理，浪费了大量人力、物力，为此有必要展开岩体微震信号自动识别的研究。

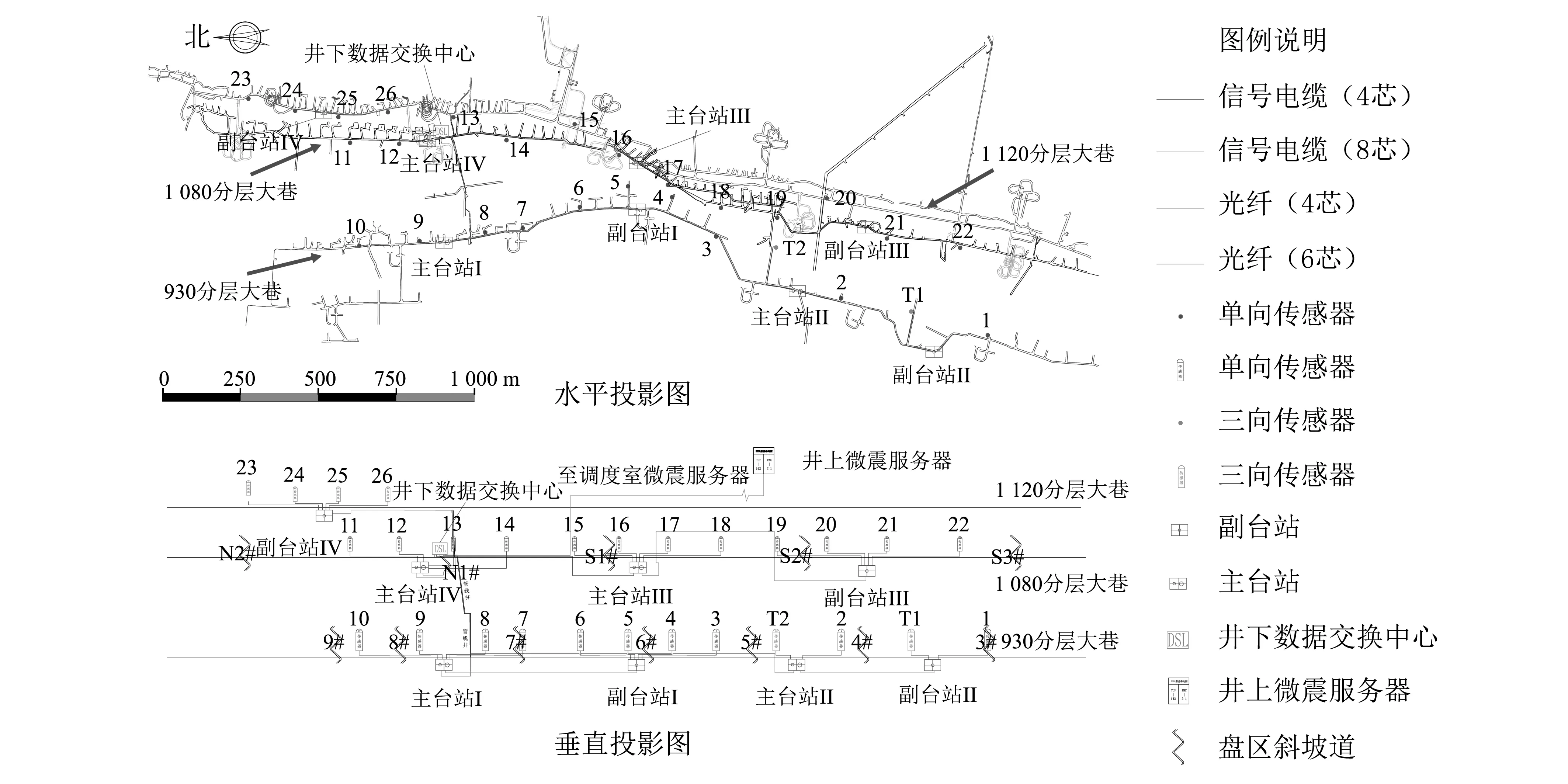
图1 用沙坝矿微震监测系统示意图Fig.1 Sketch map of microseismic monitoring system of Yongshaba mine

2.1 微震信号的频带划分

用沙坝矿岩体破裂信号与爆破振动信号典型波形分别如图2(a)和图3(a)所示，其归一化后波形的傅里叶幅值谱分别对应图2(b)和图3(b)。由图知岩体破裂信号的主频带相对较窄，主要分布于10～70 Hz，集中于15～35 Hz；爆破振动信号的主频带相对较宽，主要分布于50～290 Hz，集中于60～145 Hz。由此，根据岩体破裂信号与爆破振动信号的频谱特性，将岩体微震信号切片至0～50 Hz、50～100 Hz、100～150 Hz、150～200 Hz、200～250 Hz和大于250 Hz六个频带进行特征提取。

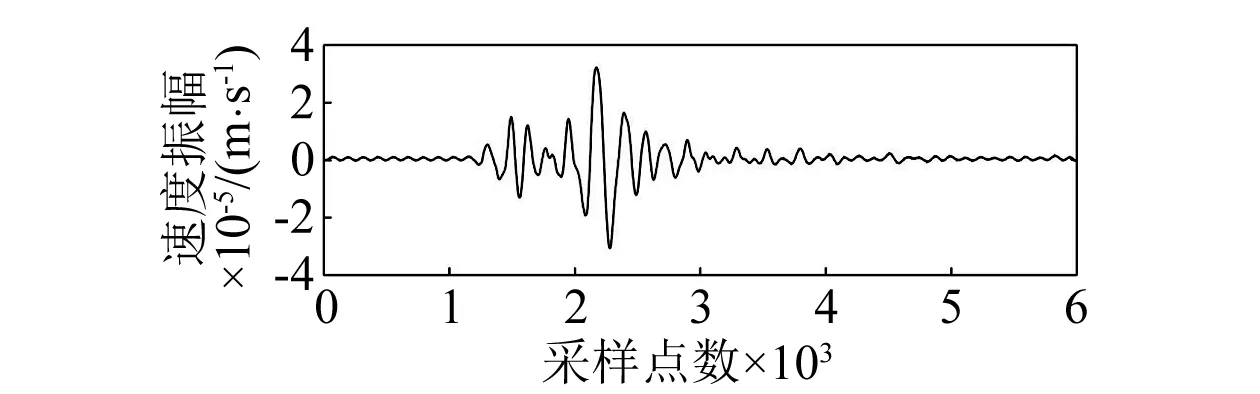
(a) 岩体破裂原始信号

(b) 岩体破裂信号归一化后幅值谱图2 岩体破裂原始信号及其归一化后幅值谱Fig.2 Waveform of rock mass fracturing signal and its amplitude spectrum after normalization

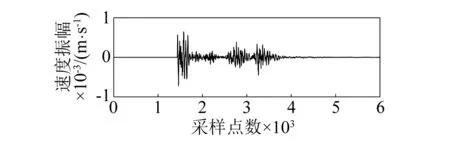
(a) 爆破振动原始信号

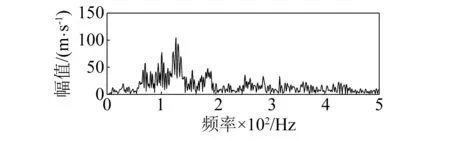
(b) 爆破振动信号归一化后幅值谱图3 爆破振动原始信号及其归一化后幅值谱Fig.3 Waveform of blasting vibration signal and its amplitude spectrum after normalization

2.2FSWT信号切片与重构

由图4得到岩体破裂归一化后各频带重构信号速度振幅峰值分别为1.058 0、0.211 6、0.026 0、0.005 9、0.001 8和0.011 5 m/s；爆破振动归一化后各频带重构信号速度振幅峰值分别为0.082 3、0.322 6、0.625 3、0.966 0、0.077 5和0.398 1 m/s。可知岩体破裂振动强度随频带增大而整体逐渐减小，而爆破振动强度随频带增加呈现先增大再减小的趋势。

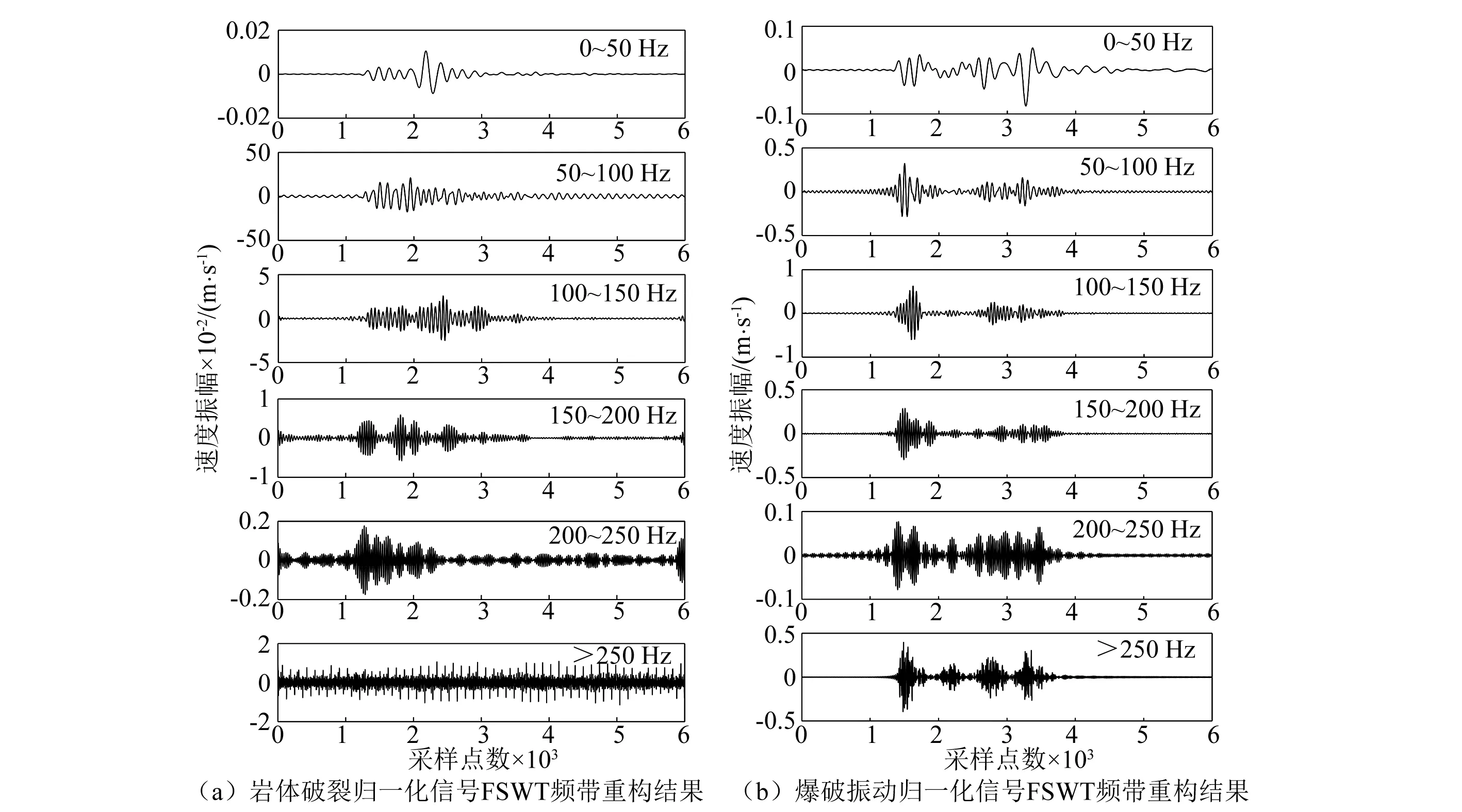
图4 岩体破裂和爆破振动归一化信号FSWT频带重构结果Fig.4 Reconstructed results of the normalized rock mass fracturing signal and the blasting vibration signal using the FSWT

2.3 FSWT-SVD特征分析

由图4知，FSWT频带重构信号包含了多维信息，采用SVD对重构信号矩阵X求奇异值，得到120个岩体破裂事件和120个爆破振动事件传播距离最近信号的奇异值箱形图(图5)。箱形图能有效反映数据的分散情况，可用于研究数据的差异性[35]。箱形图包括异常值、上边缘、上四分位数(Q3)、中位数、下四分位数(Q1)、四分位距(IQR)和下边缘等特征值，其中异常值指不在区间[Q1-1.5IQR, Q3+1.5IQR]的值，上四分位数Q3指75%的数据小于等于此值，中位数指50%的数据小于等于此值，下四分位数Q1指25%的数据小于等于此值。

由图5知，岩体破裂信号与爆破振动信号的奇异值σ1相差最大，σ2、σ4、σ5和σ6相差较大，而σ3差异不明显。上述分析只对奇异值识别岩体破裂与爆破振动作了定性阐述，为得到最优的微震信号识别结果，本文尝试对奇异值混叠较严重部分(σ1:7～10、σ2:3～6、σ3:0.5～2、σ4:0.5～2、σ5:0.5～1.7和σ6:0.3～0.9)进行等间隔取值，进而采用单一奇异值分界值法进行分类。单一奇异值分界值法取某一奇异值在特定范围为岩体破裂信号，反之则为爆破振动信号，例如σ1=7作为单一奇异值分界值时：σ1>7均为岩体破裂信号；σ1≤7均为爆破振动信号，进而得到不同分界值下岩体破裂和爆破振动信号识别正确数和整体准确率(表1)。

图5 岩体破裂信号与爆破振动信号的奇异值箱型图Fig.5 Box graphs of singular values of rock mass fracturing signals and blasting vibration signals

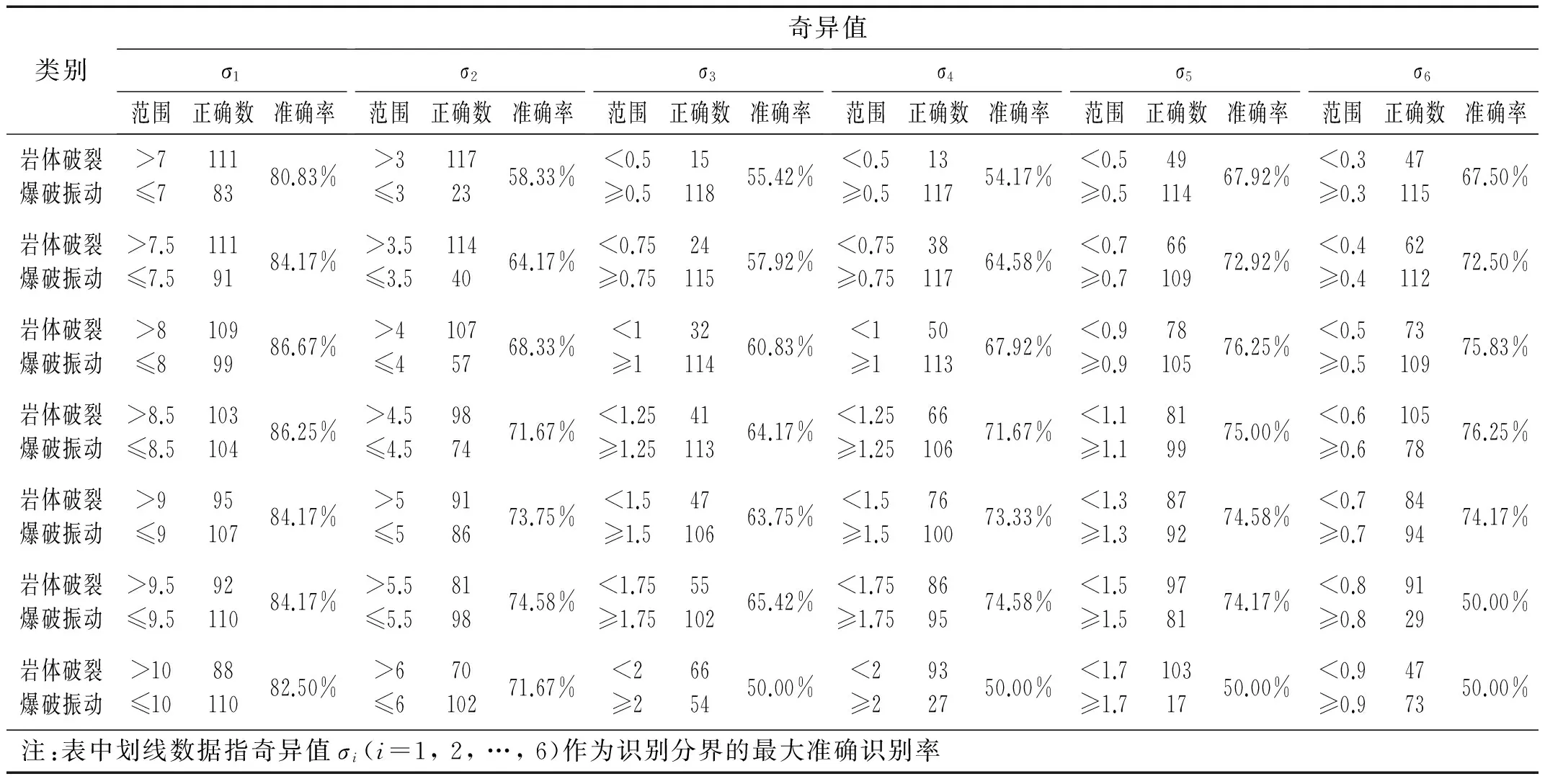
类别奇异值σ1范围正确数准确率σ2范围正确数准确率σ3范围正确数准确率σ4范围正确数准确率σ5范围正确数准确率σ6范围正确数准确率岩体破裂爆破振动>7≤71118380.83%>3≤31172358.33%<0.5≥0.51511855.42%<0.5≥0.51311754.17%<0.5≥0.54911467.92%<0.3≥0.34711567.50%岩体破裂爆破振动>7.5≤7.51119184.17%>3.5≤3.51144064.17%<0.75≥0.752411557.92%<0.75≥0.753811764.58%<0.7≥0.76610972.92%<0.4≥0.46211272.50%岩体破裂爆破振动>8≤81099986.67%>4≤41075768.33%<1≥13211460.83%<1≥15011367.92%<0.9≥0.97810576.25%<0.5≥0.57310975.83%岩体破裂爆破振动>8.5≤8.510310486.25%>4.5≤4.5987471.67%<1.25≥1.254111364.17%<1.25≥1.256610671.67%<1.1≥1.1819975.00%<0.6≥0.61057876.25%岩体破裂爆破振动>9≤99510784.17%>5≤5918673.75%<1.5≥1.54710663.75%<1.5≥1.57610073.33%<1.3≥1.3879274.58%<0.7≥0.7849474.17%岩体破裂爆破振动>9.5≤9.59211084.17%>5.5≤5.5819874.58%<1.75≥1.755510265.42%<1.75≥1.75869574.58%<1.5≥1.5978174.17%<0.8≥0.8912950.00%岩体破裂爆破振动>10≤108811082.50%>6≤67010271.67%<2≥2665450.00%<2≥2932750.00%<1.7≥1.71031750.00%<0.9≥0.9477350.00%注:表中划线数据指奇异值σi(i=1,2,…,6)作为识别分界的最大准确识别率

由表1知：σ1作为识别分界效果最好，且σ1=8时识别准确率达到了86.67%；σ3作为识别分界效果最差，最高准确率仅为65.42%；而σ2、σ4、σ5和σ6作为识别分界效果差别不大，最高准确率分别为74.58%、74.58%、76.25%和76.25%。综上知，选取奇异值σ1=8作为分界值时，可达到最优识别准确率为86.67%。

然而寻找最优奇异值分界值的工作量较大，且采用等间隔取值得到的最优值并不一定是全局最优值。此外，由单一奇异值分界值法结果知，各奇异值对微震识别均有一定的贡献。为此，本文借助机器学习法能有效挖掘数据内在信息，从而识别岩体微震信号的特点，选取BP神经网络机器学习法对岩体微震信号展开分类分析，以期得到较好的识别效果。

3 基于FSWT-SVD的BP神经网络模式识别

3.1 基于FSWT-SVD的BP神经网络模型的建立

BP神经网络是一种按误差逆传播算法训练的多层前馈网络，其能学习和贮存大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程[36]。神经网络模型拓扑结构包括输入层(input layer)、隐含层(hide layer)和输出层(output layer)。本文建立了基于FSWT-SVD的3层BP神经网络模型，其拓扑结构如图6所示。

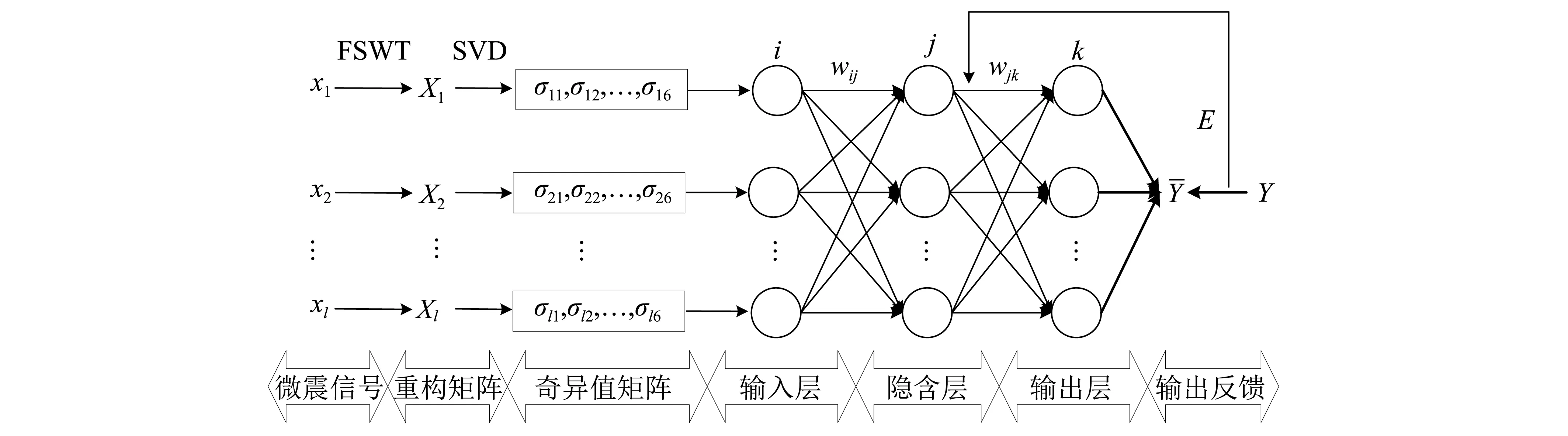
图6 基于FSWT-SVD的3层BP神经网络拓扑结构图Fig.6 Topological structure of three layers BP netural networks based on FSWT-SVD model

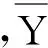
3.2 不同机器学习法识别结果

下文中分类识别均分别选取岩体破裂和爆破振动信号的1～70组数据作为机器学习法训练样本，71～120组数据作为预测样本。设定岩体破裂信号的标识类别为0，爆破振动信号的标识类别为1。

为测试BP法分类效果的优越性，本文选取三种常用的机器学习法——Logistic Regression(LR)、Bayes和Fisher法的分类结果作为对比。BP神经网络参数如下：冲量系数0.7，网络结构为6个输入节点、3个隐层节点和1个输出节点。Bayes和Fisher分类的先验概率均为0.5。不同机器学习法识别结果如表2所示。

由表2知：四种机器学习法的分类识别效果均较好，准确率达到了88%以上，优于单一奇异值分界值法的最大准确率86.67%。此外，BP法训练组和预测组准确率均高于LR法、Bayes法和Fisher法，表明BP法对微震信号分类最为有效。

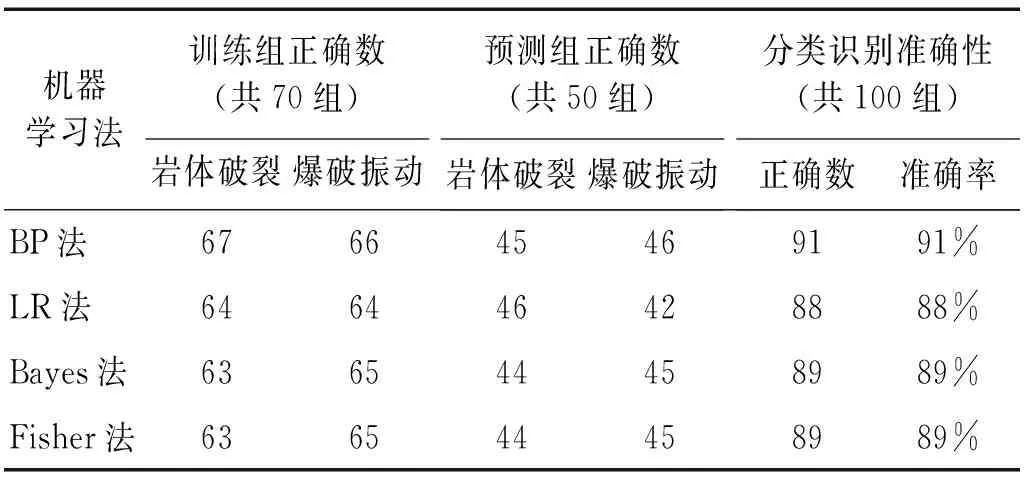
表2 不同机器学习法识别结果统计

3.3 不同特征指标识别结果

为测试SVD提取特征的优越性，本文对FSWT切片重构信号所组成的频带矩阵奇异值、频带能量比和频带相关系数[38]展开神经网络训练和预测，得到基于奇异值、能量比和相关系数的分类识别效果表3所示。

由表3知：奇异值法训练组正确数稍高于能量比法和相关系数法，但奇异值法预测组效果较能量比法和相关系数法优势明显，即奇异值法识别效果最优，且分类识别准确率达到了91%。

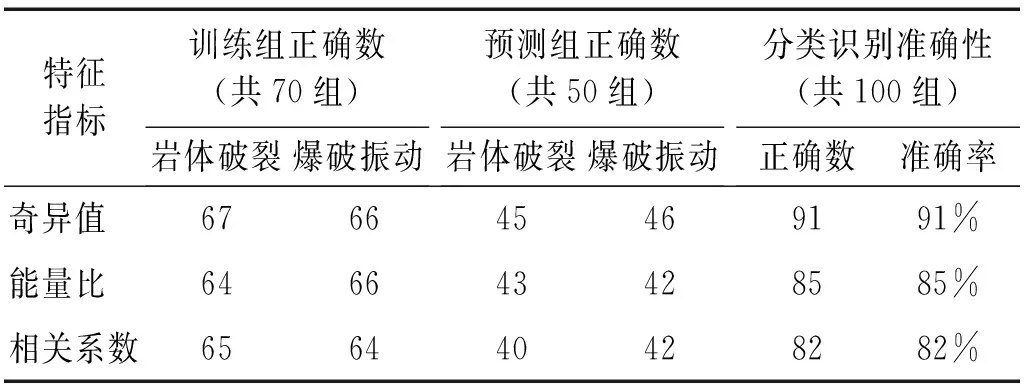
表3 不同特征指标识别结果统计

3.4 不同特征矩阵识别结果

为测试FSWT重构的优越性，本文选取离散小波变化(Discrete Wavelet Transform，DWT)主要重构部分(D3～D8)组成矩阵的奇异值识别效果作为对比，得到不同特征矩阵识别结果如表4所示。由表4知FSWT重构信号组成矩阵识别结果优于DWT重构结果。

表4 不同特征矩阵识别结果统计

4 结 论

本文采用FSWT-SVD模型提取岩体破裂信号与爆破振动信号特征，并用BP神经网络对岩体微震信号展开模式识别，主要结论如下：

(1) FSWT实现了岩体微震信号在不同频带的精确重构，SVD分解得到了重构频带信号所组成矩阵的奇异值，并以此作为识别岩体微震信号的定量表征。FSWT-SVD模型为获取岩体微震信号特征、研究矿山信号模式识别提供了一种新思路。

(2) 信号的奇异值矩阵反映了信号的特征，不同类别的岩体微震信号具有不同的奇异值。岩体破裂信号与爆破振动信号重构频带信号构成矩阵的奇异值σ1相差最大，σ2、σ4、σ5和σ6相差较大，而σ3差异不明显，且取σ1=8作为单一奇异值法识别分界值时分类效果最优，准确率达到了86.67%。

(3) BP神经网络法分类识别结果较LR法、Bayes法和Fisher法优，SVD提取特征识别效果较能量比和相关系数优，FSWT重构矩阵提取的特征信息优于DWT重构矩阵提取的特征信息，且基于FSWT-SVD的BP法分类识别准确率达到了91%。由此表明：基于BP神经网络的FSWT-SVD模型识别岩体破裂信号与爆破振动信号是可行的，具有较高的准确率。

[1] DONG L, LI X, XIE G. Nonlinear methodologies for identifying seismic event and nuclear explosion using random forest, support vector machine, and naive Bayes classification[J]. Abstract and Applied Analysis, 2014, 2014: 459137.

[2] DONG L, WESSELOO J, POTVIN Y, et al. Discrimination of mine seismic events and blasts using the Fisher classifier, Naive Bayesian classifier and logistic regression[J]. Rock Mechanics and Rock Engineering, 2016, 49(1): 183-211.

[3] GULIA L. Detection of quarry and mine blast contamination in European regional catalogues[J]. Natural Hazards, 2010, 53(2): 229-249.

[4] 朱权洁, 姜福兴, 尹永明, 等. 基于小波分形特征与模式识别的矿山微震波形识别研究[J]. 岩土工程学报, 2012, 34(11): 2036-2042. ZHU Quanjie, JIANG Fuxing, YIN Yongming, et al. Classification of mine microseismic events based on wavelet-fractal method and pattern recognition[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(11): 2036-2042.

[6] 曹安业, 窦林名, 秦玉红, 等. 高应力区微震监测信号特征分析[J]. 采矿与安全工程学报, 2007, 24(2): 146-149. CAO Anye, DOU Linming, QIN Yuhong, et al. Characteristic of microseismic monitoring signal in high stressed zone[J]. Journal of Mining & Safety Engineering, 2007, 24(2): 146-149.

[7] ALLMANN B P, SHEARER P M, HAUKSSON E. Spectral discrimination between quarry blasts and earthquakes in Southern California[J]. Bulletin of the Seismological Society of America, 2008, 98(4): 2073-2079.

[8] 陆菜平, 窦林名, 吴兴荣, 等. 煤岩冲击前兆微震频谱演变规律的试验与实证研究[J]. 岩石力学与工程学报, 2008, 27(3): 519-525. LU Caiping, DOU Linming, WU Xingrong, et al. Experimental and empirical research on frequency- spectrum evolvement rule of rockburst precursory microseismic signals of coal-rock [J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 519-525.

[9] 唐守锋, 童敏明, 潘玉祥, 等. 煤岩破裂微震信号的小波特征能谱系数分析法[J]. 仪器仪表学报, 2011, 32(7): 1521-1527. TANG Shoufeng, TONG Minming, PAN Yuxiang, et al. Energy spectrum coefficient analysis of wavelet features for coal rupture microseismic signal[J]. Chinese Journal of Scientific Instrument, 2011, 32(7): 1522-1527.

[10] 朱权洁, 姜福兴, 于正兴, 等. 爆破震动与岩石破裂微震信号能量分布特征研究[J].岩石力学与工程学报, 2012, 31(4): 723-730. ZHU Quanjie, JIANG Fuxing, YU Zhengxing, et al. Study on energy distribution characters about blasting vibration and rock fracture microseismic signal[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(4): 723-730.

[11] 毕明霞, 黄汉明, 边银菊, 等. 天然地震与人工爆破波形信号HHT特征提取和SVM识别研究[J]. 地球物理学进展, 2011, 26(4): 1157-1164. BI Mingxia, HUANG Hanming, BIAN Yinju, et al. A study on seismic signal HHT features extraction and SVM recognition of earthquake and explosion[J]. Progress in Geophysics, 2011, 26(4): 1157-1164.

[12] 毕明霞, 黄汉明, 边银菊, 等. 基于经验模态分解的地震波特征提取的研究[J]. 地球物理学进展, 2013, 27(5): 1890-1896. BI Mingxia, HUANG Hanming, BIAN Yinju, et al. Study on seismic signal features extraction based on EMD[J]. Progress in Geophysics, 2012, 27(5): 1890-1896.

[13] 李舜酩, 郭海东, 李殿荣. 振动信号处理方法综述[J]. 仪器仪表学报, 2013, 34(8): 1907-1915. LI Shunming, GUO Haidong, LI Dianrong. Review of vibration signal processing methods[J]. Chinese Journal of Scientific Instrument, 2013, 34( 8): 1907-1915.

[14] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society, 1998, 454(1971): 903-995.

[15] YAN Z, MIYAMOTO A, JIANG Z. Frequency slice wavelet transform for transient vibration response analysis[J]. Mechanical Systems & Signal Processing, 2009, 23(5): 1474-1489.

[16] YAN Z, MIYAMOTO A, JIANG Z, et al. An overall theoretical description of frequency slice wavelet transform[J]. Mechanical Systems and Signal Processing, 2010, 24(2): 491-507.

[17] YAN Z, MIYAMOTO A, JIANG Z. Frequency slice algorithm for modal signal separation and damping identification[J]. Computers & Structures, 2011, 89(1): 14-26.

[18] 钟先友, 赵春华, 陈保家, 等. 基于形态自相关和时频切片分析的轴承故障诊断方法[J]. 振动与冲击, 2014, 33(4): 11-16. ZHONG Xianyou, ZHAO Chunhua, CHEN Baojia, et al. Bearing fault diagnosis method based on morphological filtering, time-delayed autocorrelation and time-frequency slice analysis[J]. Journal of Vibration and Shock, 2014, 33(4): 11-16.

[19] 郭涛, 方向, 谢全民, 等. 频率切片小波变换在爆破振动信号时频特征精确提取中应用[J]. 振动与冲击, 2013, 32(22): 73-78. GUO Tao, FANG Xiang, XIE Quanmin, et al. Application of FSWT in accurate extraction of time-frequency features for blasting vibration signals[J]. Journal of Vibration and Shock, 2013, 32(22): 73-78.

[20] 段晨东，高强．基于时频切片分析的故障诊断方法及应用[J]. 振动与冲击, 2011, 30 (9): 1-5. DUAN Chendong, GAO Qiang. Noval fault diagnosis approach using time-frequency slice analysis and its application[J]. Journal of Vibration and Shock, 2011, 30 (9): 1-5.

[21] 段晨东, 高强, 徐先峰. 频率切片小波变换时频分析方法在发电机组故障诊断中的应用[J]. 中国电机工程学报, 2013, 33(32): 96-103. DUAN Chendong, GAO Qiang, XU Xianfeng. Generator unit fault diagnosis using the frequency slice wavelet transform time-frequency analysis method[J]. Proceedings of the CSEE, 2013, 33(32): 96-103.

[22] AI L, WANG J, YAO R. Classification of parkinsonian and essential tremor using empirical mode decomposition and support vector machine[J]. Digital Signal Processing, 2011, 21(4): 543-550.

[23] 徐锋, 刘云飞. 基于 EMD-SVD 的声发射信号特征提取及分类方法[J]. 应用基础与工程科学学报, 2014, 22(6): 1238-1247. XU Feng, LIU Yunfei. Feature extraction and classification method of acoustic emission signals generated from plywood damage based on EMD-SVD[J]. Journal of Basic Science and Engineering, 2014, 22(6): 1238-1247.

[24] 徐锋, 刘云飞, 宋军. 基于中值滤波-SVD和EMD的声发射信号特征提取[J]. 仪器仪表学报, 2011, 32(12): 2712-2719. XU Feng, LIU Yunfei, SONG Jun. Feature extraction of acoustic emission signals based on median filter-SVD and EMD[J]. Chinese Journal of Scientific Instrument, 2011, 32(12): 2712-2719.

[25] 丁建明, 王晗, 林建辉, 等. 基于 EMD-Hankel-SVD 的高速列车万向轴动不平衡检测[J]. 振动与冲击, 2015, 34(9): 164-170. DING Jianming, WANG Han, LIN Jianhui, et al. Detection of dynamic imbalance due to cardan shaft in high-speed train based on EMD-Hankel-SVD method[J]. Journal of Vibration and Shock, 2015, 34(9): 164-170.

[26] 丁建明, 林建辉, 赵洁. 高速列车万向轴动不平衡检测的 EEMD-Hankel-SVD 方法[J]. 机械工程学报, 2015, 51(10): 143-151. DING Jianming, LIN Jianhui, ZHAO Jie. Detection of the dynamic imbalance with cardan shaft in high-speed train applying EEMD-Hankel-SVD[J]. Journal of Mechanical Engineering, 2015, 51(10): 143-151.

[27] ZHANG Y, ZUO H, BAI F. Classification of fault location and performance degradation of a roller bearing[J]. Measurement, 2013, 46(3): 1178-1189.

[28] YANG Z X, ZHONG J H. A hybrid EEMD-based SampEn and SVD for acoustic signal processing and fault diagnosis[J]. Entropy, 2016, 18(4): 112.

[29] 姜久亮, 刘文艺, 侯玉洁, 等. 基于内积延拓 LMD 及 SVM 的轴承故障诊断方法研究[J]. 振动与冲击, 2016, 35(6): 104-108. JIANG Jiuliang, LIU Wenyi, HOU Yujie, et al. Bearing fault diagnosis based on integral waveform extension LMD and SVM[J]. Journal of Vibration and Shock, 2016, 35(6): 104- 108.

[30] TIAN Y, MA J, LU C, et al. Rolling bearing fault diagnosis under variable conditions using LMD-SVD and extreme learning machine[J]. Mechanism and Machine Theory, 2015, 90: 175-186.

[31] 赵学智, 叶邦彦, 陈统坚. 基于小波-奇异值分解差分谱的弱故障特征提取方法[J]. 机械工程学报, 2012, 48(7): 37-48. ZHAO Xuezhi, YE Bangyan, CHEN Tongjian. Extraction method of faint fault feature based on Wavelet-SVD difference spectrum[J]. Journal of Mechanical Engineering, 2012, 48(7): 37-48.

[32] JIANG Y, TANG B, QIN Y, et al. Feature extraction method of wind turbine based on adaptive Morlet wavelet and SVD[J]. Renewable Energy, 2011, 36(8): 2146-2153.

[33] 朱军, 闵祥敏, 孔凡让, 等. 基于分量筛选奇异值分解的滚动轴承故障诊断方法研究[J]. 振动与冲击, 2015, 34(20): 61-65. ZHU Jun, MIN Xiangmin, KONG Fanrang, et al. Rolling bearing fault diagnosis based on component screening singular value decomposition[J]. Journal of Vibration and Shock, 2015, 34(20): 61-65.

[34] LIU H, WANG X, LU C. Rolling bearing fault diagnosis under variable conditions using Hilbert-Huang transform and singular value decomposition[J]. Mathematical Problems in Engineering, 2014, 2014: 765621.

[35] MCGILL R, TUKEY J W, LARSEN W A. Variations of box plots[J]. The American Statistician, 1978, 32(1): 12-16.

[36] MCCLELLAND J L, RUMELHART D E, PDP Research Group. Parallel distributed processing[M]. IEEE,1988.

[37] RUMELHART D E, HINTON G E, WILLIAMS R J. Learning internal representations by error propagation[R]∥ Parallel distributed processing: explorations in the microstructure of cognition, vol 1. Cambridge, MA, USA: MIT Press, 1986:318-362.

[38] 赵志宏, 杨绍普, 申永军. 基于独立分量分析与相关系数的机械故障特征提取[J]. 振动与冲击, 2013, 32(6): 67-72. ZHAO Zhihong, YANG Shaopu, SHEN Yongjun. Machinery fault feature extraction based on independent component analysis and correlation coefficient [J]. Journal of Vibration and Shock, 2013, 32(6): 67-72.

Application of FSWT-SVD model in the feature extraction of rock mass microseismic signals

SHANG Xueyi1, LI Xibing1, PENG Kang2,3, WANG Zewei1, WENG Lei1

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China; 2. State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing 400044, China;3. College of Resources and Environmental Science, Chongqing University, Chongqing 400030, China)

Viewing that it is difficult to identify rock mass fracturing signals and blasting vibration signals, the Fourier transform (FT) was applied to gain their spectrum distributions and six frequency bands were determined for the feature extraction analysis. Then the rock mass fracturing signals were divided and reconstructed by the frequency slice wavelet transform (FSWT), and the singular value decomposition (SVD) was employed to obtain the singular valuesσi(i=1,2,…,6) of matrixes composed of the six reconstructed components, thus the feature extraction of rock mass fracturing signals was implemented. Furthermore, 120 sets of rock mass fracturing signals and 120 sets of blasting vibration signals obtained from the Yongshaba mine were analysed by using the FSWT-SVD method. Finally, a back propagation (BP) neural network was adopted to train, classify and recognize the eigenvectors obtained from the singular values. The results show that: there are large difference inσ1, comparatively large differences inσ2,σ4,σ5andσ6, and little difference inσ3between rock mass fracturing signals and blasting vibration signals, and the best pattern recognition will be obtained whenσ1is equal to eight with an accuracy rate of 86.67%; the classification result based on BP neural network is the best among the BP, logistic regression (LR), Bayes and Fisher based methods, the feature matrix obtained by the SVD is better than that obtained by the energy ratio and correlation coefficient matrix, and the feature matrix obtained by the FSWT is better than that by the discrete wavelet transform (DWT). Furthermore, the BP classifier based on FSWT-SVD achieves a correct identification rate of 91%. In conclusion, the BP classifier based on FSWT-SVD provides a new way for the feature extraction and pattern recognition of rock mass fracturing signals and blasting vibration signals.

rock mass microseismic signal；frequency slice wavelet transform；singular value decomposition；feature extraction；pattern recognition

国家重点研发计划(2016YFC0600706); 国家自然科学基金青年基金(51504044); 湖南省研究生创新项目(CX2017B054); 中央高校基本科研基金(2015CDJXY); 中国博士后面上基金(2015M570607)

2016-03-21 修改稿收到日期： 2016-05-17

尚雪义 男，博士生，1989年生

李夕兵 男，博士，长江学者特聘教授，1962年生

E-mail: xbli@mail.csu.edu.cn

TD 32

A

10.13465/j.cnki.jvs.2017.14.008