一种聚类优化的传感器布置方法研究

张 恒， 李世其， 刘世平， 张 哲， 王 跃

(华中科技大学 机械科学与工程学院，武汉 430074)

一种聚类优化的传感器布置方法研究

张 恒， 李世其， 刘世平， 张 哲， 王 跃

(华中科技大学 机械科学与工程学院，武汉 430074)

复杂结构试验/理论振型的匹配是模态参数型修正过程的重要内容。以测量并获取用于模态参数识别的最佳信息为目标，实现布置在结构上有限数量的传感器能有效避免信息冗余，提出了一种聚类优化的传感器布置方法。根据结构模态中各自由度振型的动力相似性，应用k-means聚类算法对自由度进行自动集结并分类。采用有效独立法分别从各聚类自由度中搜索出模态分辨率最高的传感器位置作为实际的测量位置。最后通过一个悬臂梁、一个悬臂薄板的数值分析和一个旋转滤光轮组件的模态测试试验对该优化布置方法进行验证。分析结果表明，这种方法能有效选出独立敏感性测点，并且具有较高的搜索效率。

传感器布置；k-means聚类；有效独立法；模态试验；模型验证

航天器结构模型试验验证是结构计算模型修正技术必须解决的关键性问题。其中，试验模态参数的辨识精度很大程度上决定了模型修正技术的成败和效率，而高质量的测试数据则是试验模态参数辨识精度的保障[1]。随着大型机械结构日益复杂，结构理论与试验模型匹配的难度迅速加大。目前采用的对策是在模型试验验证过程中，利用结构的先验理论模型进行测试传感器的优化配置，选择模态分辨率最高的传感器位置作为实际的测量位置，使理论与实验模型满足高度的相关性，从而准确获取试验验证模型[2]。传统的传感器优化配置方法是一种次优化方法。Kammer根据Fisher信息矩阵行列式最大化的思想提出了一种有效独立法[3]，通过迭代删除独立贡献最小的自由度最终确定传感器的数目，这种方法可扩展应用于三向加速度传感器的布置过程[4]。能量法是根据结构自由度的模态动能或单元应变能选择传感器的位置[5]。Papadimitriou提出一种基于信息熵指标的传感器优化方法，该方法是把模态参数估计的不确定性用信息熵指标来度量，通过度量值的最小原则选择传感器[6]。然而，这些传感器优化布置方法对自由度数目的选取依赖试验者的主观经验，当采用传感器的数目大于感兴趣的模态阶数时，优化方法选择的传感器表现出明显的聚类特性[7]，并且过多的传感器布置将不可避免引入冗余信息[8]。从工程应用方面考虑，单纯采用这些优化方法并不理想。聚类算法为传感器的优化选择提供了一种新途径，采用k-means聚类算法可对动力相似性的自由度进行自动集结分类，从而避免了对自由度数目的主观选择[9]。

针对以上分析，本研究根据结构中各自由度振型的动力相似性，采用k-means聚类算法对自由度进行自动分类，采用有效独立法实现传感器的优化布置。以一个悬臂梁和一个悬臂板的数值仿真和一个滤光轮组件的模态试验为例，对传感器测点选择与优化布置方法进行探讨，为有效获得结构敏感振动状态信息提供参考。

1 基本理论

1.1 计算模型

定义一个n自由度结构动力系统，其运动方程可表示为

(-ω2[M]+iω[C]+[K]X(ω)=F(ω)

(1)

式中：[M]、[C]、[K]分别表示结构的质量、阻尼和刚度矩阵；F(ω)为外载荷向量。对于无阻尼自由振动系统，由n个特征值0≤λ1≤λ2≤…≤λn及其对应的特征向量{φ1，φ2,…，φn}构成的特征方程为

[K]φ=λ[M]φ

(2)

由动力分析模态叠加原理可知，结构的响应可以表示为

{x}=Φ{q}

(3)

式中：{x}为结构的响应向量；Φ为模态振型矩阵，{q}为模态坐标向量。

1.2k-means聚类算法

自由度的动力相似性主要表现为某些自由度在重要模态中的振型值相近，这些自由度在动力载荷作用下的响应也将近似相等。因此，可根据结构中各自由度在重要模态中振型值的相似度进行自动类别划分。k-means聚类算法是以衡量分类结果的标准测度函数作为聚类分析的收敛条件，标准测度函数通常采用欧氏距离平方和的形式表述

(4)

式中：k为类别总数；φ为属于第i类振型Φi的振型值；mi为类别Φi的中心。

对k-means算法的步骤具体描述如下：①在振型集合Φ中任选k个样本作为k个初始聚类中心；②对于其余非聚类中心的振型值，根据他们与这些聚类中心的相似度(欧氏距离)，分别将他们划分至与其最相近的聚类中心所在的类别；③更新每个类别的聚类中心(该聚类中所有振型值的均值)；④重复步骤②～③，直至标准测度函数E收敛。

1.3 有效独立法

有效独立法(EFI)的基本思想是从所有可能的测点出发，使选择的测点能保留目标模态具有最大的线性无关性。该矩阵可表述为

Q=φTφ

(5)

根据矩阵行列式最大准则来评价构造的Fisher信息矩阵，采用逐步消除法进行迭代搜索，测点的选择依赖有效独立矩阵D，D可表述为

D=φQ-1φT

(6)

D为幂等矩阵，它的迹等于秩，其对角线上的元素Di表示第i个测点对矩阵D的贡献。每次删除独立贡献最小的值，即

det(Q)=det(Q0)(1-Di)

(7)

式中：Q0为初始Fisher信息矩阵，则在模态振型矩阵φ中删除对应的列向量，这样就能从全部的待选测点中逐步删除有效独立贡献最小的测点，保留对振型有效独立贡献较大的测点。

2 传感器聚类优化布置方法设计

传感器优化布置的目的是使获得的模态空间估计最佳，常采用模态振型构建反映结构动态特性的Fisher信息矩阵。然而，当两个传感器在同一方向上获得的振型值相近时，选择一个传感器即可表征该方向上的振动状态信息。本研究根据重要模态中振型值的相似性，采用k-means聚类算法对自由度进行自动集结分类，在各聚类自由度中采用有效独立逐步删除对目标模态线性支持度较小的测点，最终得到传感器的最优布置方案。该方法的流程如图1所示，具体的算法描述如下：

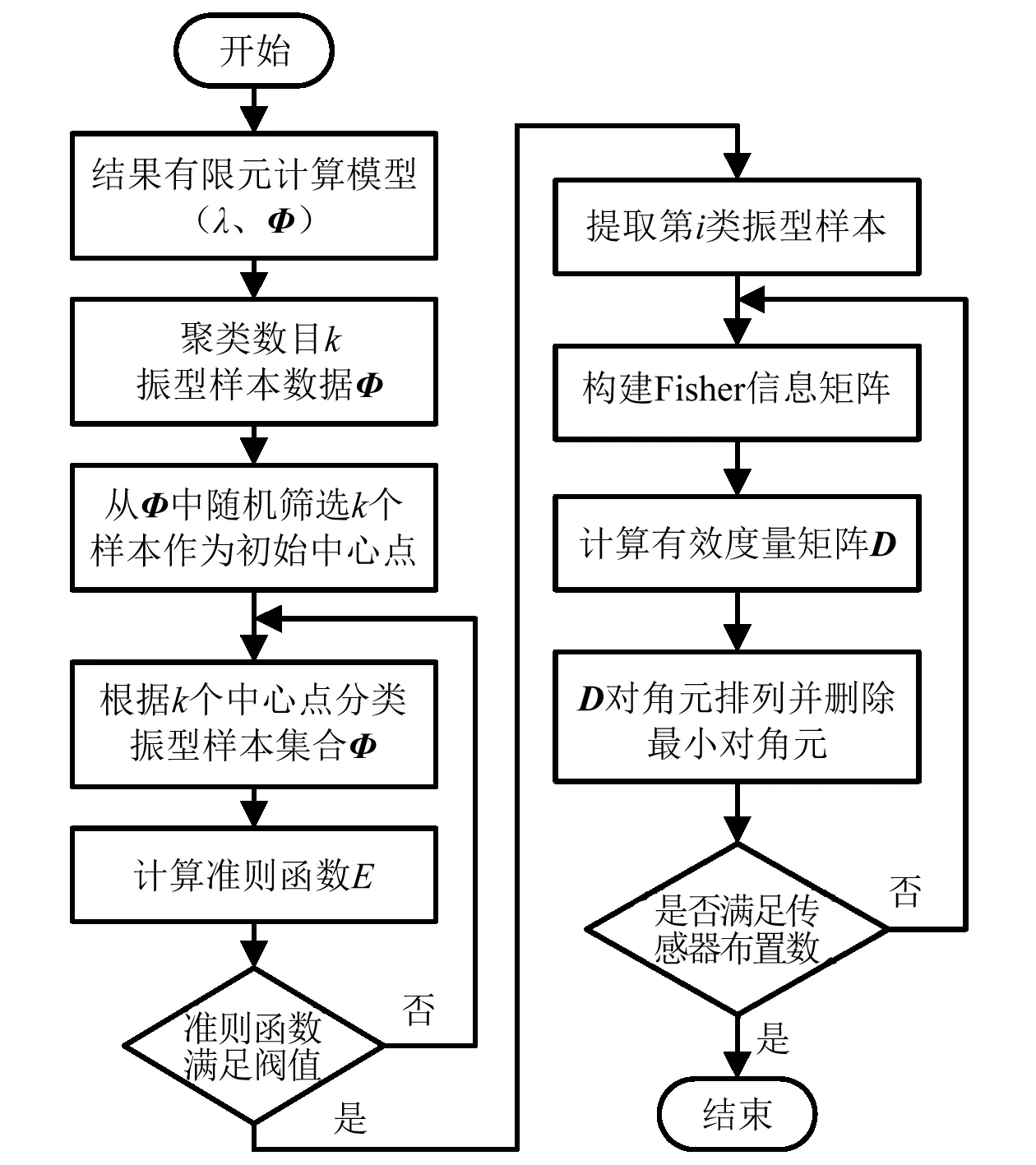
图1 传感器优化布置流程图Fig.1 Flow chart of optimal sensor placement

步骤1 建立结构有限元分析计算模型，确定自由度数Ns，计算结构各阶模态振型φ，并选择出重要模态数Nm；

步骤2 以重要模态振中的振型值作为样本属性，采用k-means聚类算法将各自由度进行自动分类，以标准测度函数E为判据，直至准则函数满足收敛条件；

步骤3 对每一个聚类样本采用有效独立法，计算待选传感器的有效度量D，根据Di大小删除对应有效独立贡献值最小的测点，重复步骤3直到达到要求的测点数，从而以尽可能少的传感器测量获得更多的结构振动信息。

3 数值算例

3.1 算例1：简单梁

分析了文献[7]中的算例，采用一个悬臂梁用于描述本研究提出方法的数值性能。悬臂梁总长0.530 7 m，矩形截面尺寸为0.003 2 m×0.001 9 m，材料密度为2 700 kg/m3，弹性模量为7.1×1 010 N/m2。有限元模型包含30个单元，总自由度数为60，根据欧拉-伯努利梁理论建立梁单元并计算获得各阶模态振型。模型的示意图如下所示。前3阶模态主要为Y方向的振动，以Y方向的30个自由度前3阶振型值为属性，采用k-means方法进行自由度聚类划分，聚类数为3。其中，隶属于相同类别的自由度用相同的符号表示，如图2(c)。

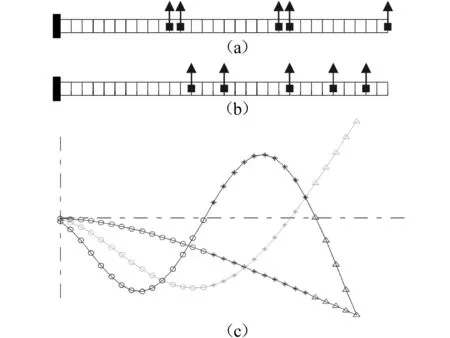
图2 悬臂梁的传感器优化布置Fig.2 Optimal sensor placement of cantilever beam

采用EFI方法分别对文献[7]中的方法和本研究提出的方法进行比较，其中，迭代删除后保留5个传感器位置。传感器的全局搜索结果与聚类逐步搜索结果见表1，测点布置情况如图2(a)和(b)。可以看出，本研究提出方法选择的传感器位置分布更加均衡，从而有效避免了传感器之间的聚类情况，使测得的结构信息更加完备。

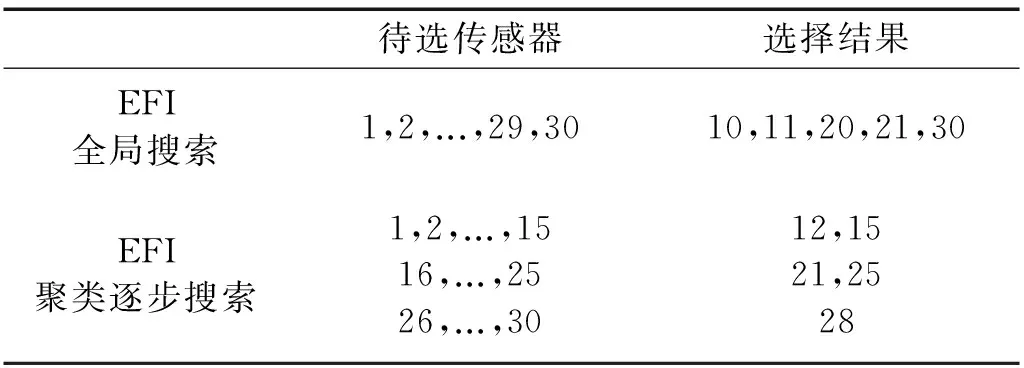
表1 两种EFI搜索方法的对比结果

3.2 算例2：悬臂板

第二个数值算例采用空间相机的次镜辐板，单个辐板可简化为简单悬臂板结构。如图3所示，悬臂板包含80个单元，100个节点(长度方向20个节点，宽度方向5个节点)。根据薄板弯曲理论，建立薄板的弯曲单元。板单元的几何参数分别为：长度a=0.02 m，宽度b=0.02 m，厚度h=0.005 m；材料参数为：弹性模量E=1.47×1 011 N/m2，材料密度ρ=8 180 kg/m3，泊松比v=0.3，通过有限元法求解悬臂板的模态。采用本研究提出的传感器优化布置过程，当聚类数分别取3和4时，测点的布置结果如图3所示。从图中可以看出，绝大多数测点布置在悬臂板的边缘，当悬臂板划分更多的聚类数时，测点的布置更加均衡，但计算量更大。

图3 悬臂板的传感器优化布置Fig.3 Optimal sensor placement of cantilever plate

4 试验分析

以空间相机旋转滤光轮组件为研究对象，开展该组件的模态分析与试验，重点分析了该组件的传感器优化布置。首先，构建该组件的有限元模型，建立的有限元模型共有11 144个单元，16 707个节点，如图4所示。由于结构内部节点无法被测量，因此待选测点仅限于滤光轮支撑结构的上表面，共计935个节点。

对该组件进行模态分析，前六阶模态为刚体模态，第七阶为轴承旋转模态，滤光轮的一阶弹性模态从第八阶模态开始，该结构的前5阶弹性模态频率见表2。对该结构的模态振型描述如下：第一阶是沿垂直面的弯曲模态；第二阶是沿对角面的弯曲模态；第三阶是沿Z方向的上下振动；第四阶是沿对角线方向的组合模态；第五阶是各方向上各阶弯曲模态的组合。

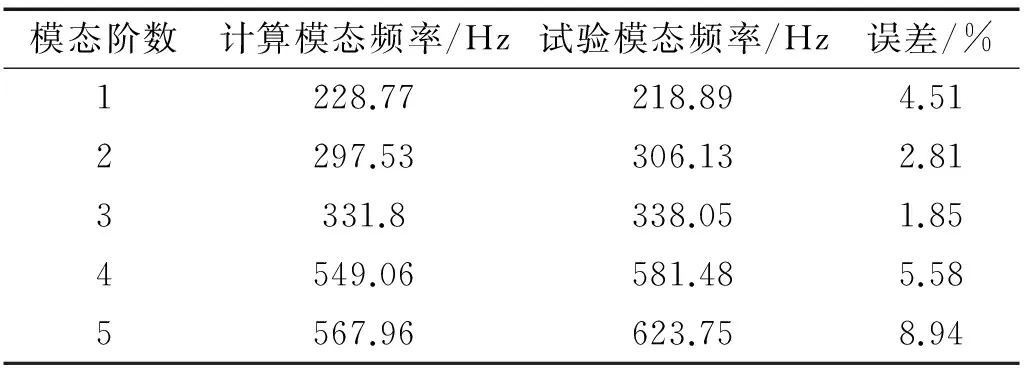
表2 滤光轮组件的前五阶模态频率

采用本研究提出的聚类优化传感器布置方法从待选测点中选出反映结构主响应特征的测点，传感器的数目为主要模态的3倍(前五阶模态为主要模态)，最终获得的15个传感器位置如图4中箭头所示。

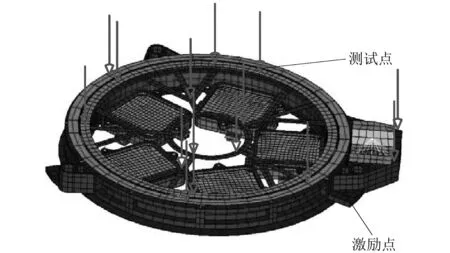
图4 旋转滤光轮组件的测点选择Fig.4 Sensor selection of the filter wheel assembly

为进一步验证模型的有效性，对滤光轮组件进行模态试验。综合上述过程获得的传感器位置，为更全

面测得结构的状态信息，在滤光轮上补充部分传感器，共采用36个加速度传感器，其实际测试如图5所示，采用力锤敲击图中所示的激励点。信号采集设备包括LMS信号采集仪和PCB三向加速度传感器，采样频率为4 096 Hz。多次测量后获得该结构的模态特征，通过辨识方法获得的试验模态频率见表2，模态测试试验振型的原始数据见表3。表3中分别列举了36个测点前五阶模态试验的振型数据。各阶振型如图6所示，从图中可以看出，滤光轮结构的实测振型与计算模态振型基本相同，说明本研究提出的传感器布置方法有效。

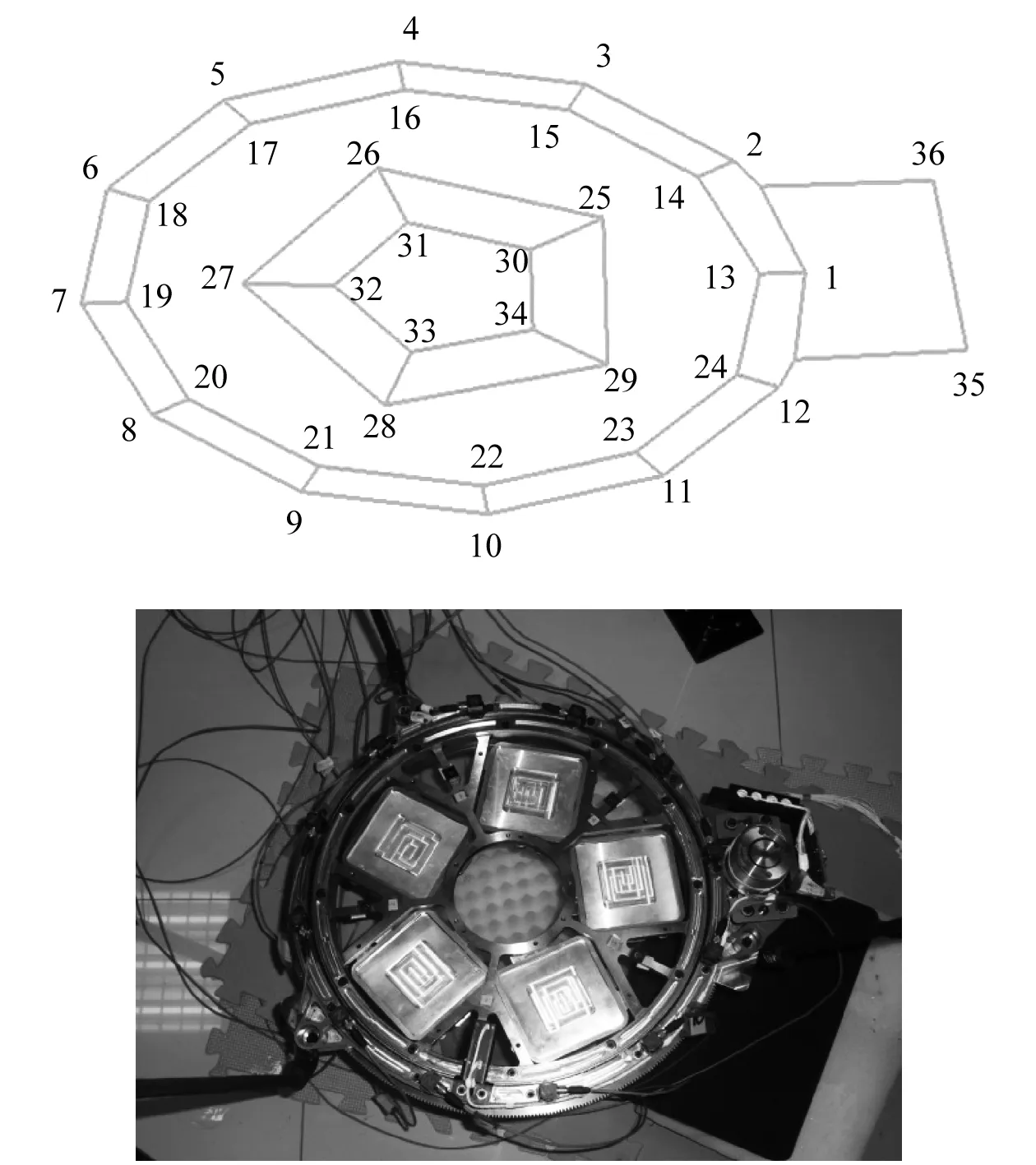
图5 滤光轮组件的实际测点布置Fig.5 Actual sensor placement of the filter wheel assembly

测点序号振型一阶振型实部虚部相位二阶振型实部虚部相位……五阶振型实部虚部相位x-2.76×10-6-2.53×10-5-96.23-2.44×10-7-3.5×10-6-93.98…-1.05×10-7-7.49×10-7-981y1.37×10-64.77×10-719.242.66×10-61.66×10-580.89…2.77×10-71.16×10-722.67z5.41×10-61.19×10-565.484.81×10-7-9.51×10-6-87.11…1.69×10-8-1.27×10-6-89.24x-3.03×10-7-1.63×10-5-91.073.21×10-61.74×10-579.57…2.27×10-7-4.52×10-763.282y7.01×10-61.14×10-558.323.83×10-67.39×10-662.63…1.99×10-79.51×10-825.51z1.46×10-6-9.03×10-6-80.81-6.86×10-6-6.56×10-5-95.97…-4.46×10-7-1.79×10-6-104.01………………………………x8.07×10-7-3.34×10-5-88.622.45×10-6-9.76×10-6-75.919.44×10-8-5.96×10-7-80.9936y-7.9×10-6-1.39×10-5-119.7-1.08×10-53.03×10-5109.58-1.05×10-7-3.08×10-7-108.89z-4.94×10-69.47×10-592.997.45×10-6-3.66×10-5-78.51-2.87×10-88.36×10-791.96

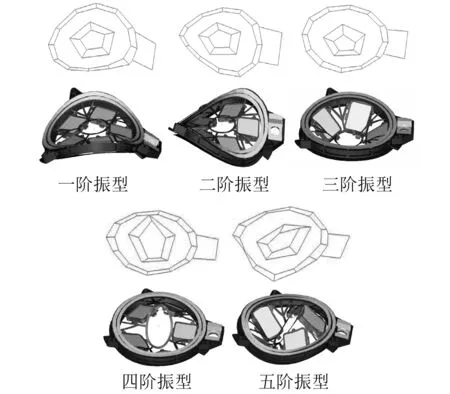
图6 滤光轮组件的前五阶模态振型Fig.6 The first five modal shape of the filter wheel assembly

5 结 论

为实现有限数量的传感器最大程度反映结构系统信息，本研究提出了一种聚类优化的传感器布置方法。该方法以结构主模态振型值为属性，采用k-means聚类算法对各自由度进行自动分类，采用有效独立法从各聚类自由度中筛选出模态分辨率最高的测点作为实际的测量位置。一个悬臂梁和一个悬臂板的数值算例分析结果表明，采用本研究提出的传感器优化布置方法能使结构上布置的测点分布更加均衡；当选取更多的分类数时，获得的布置测点更加精细，却增加的计算量。某型号航天器旋转滤光轮组件的动力学试验验证分析结果表明，本文提出的传感器优化布置方法能有效获取独立敏感性测点，并且具有较高的迭代搜索效率，该方法能为复杂结构航天器的传感器优化布置提供了一种新途径。

[1] 丁继锋，韩增尧，马兴瑞. 大型复杂航天器结构有限元模型的验证策略研究[J]. 宇航学报, 2010, 31(2): 547-555. DING Jifeng, HAN Zengyao, MA Xingrui. Finite element model verification strategy of large complex spacecraft [J]. Journal of Astronautics, 2010, 31(2): 547-555.

[2] 秦仙蓉. 基于灵敏度分析的结构计算模型修正技术及相关问题研究[D]. 南京:南京航空航天大学，2001.

[3] KAMMER D C. Sensor placement for on-orbit modal identification and correlation of large space structures [J]. Journal of Guidance, Control and Dynamics, 1991, 14(2): 251-259.

[4] KAMMER D C, TINKER M L. Optimal placement of triaxial accelerometers for modal vibration tests [J]. Mechanical Systems and Signal Processing, 2004, 18(2): 29-41.

[5] HEMEZ F M, FARHAT C. An energy based optimum sensor placement criterion and its application to structural damage detection [C]∥ Proceedings of the 12th International Conference on Modal Analysis, Society of Experimental Mechanics. Honolulu, Hawaii, 1994.

[6] PAPADIMITRIOU C, BECK J L. Entropy-based optimal sensor location for structural model updating [J]. Journal of Vibration and Control, 2000, 6(5): 781-800.

[7] FRISWELL M I, TRIGUERO R C. Clustering of sensor locations using the effective independence method [J]. AIAA Journal, 2015, 53(5): 1388-1390.

[8] SEONGMIN C, SUNGMIN B, KIM K O, et al. Structural system identification using degree of freedom-based reduction and hierarchical clustering algorithm [J]. Journal of Sound and Vibration, 2015, 346 (25): 139-152.

[9] 李成涛,肖仪清,欧进萍. 基于聚类算法和自由度集结的柔性结构模型降阶研究[J]. 计算力学学报, 2012, 29(2): 236-241. LI Chengtao, XIAO Yiqing, OU Jinping. Study on the model reduction for flexible structure based on clustering algorithm and DOFs concentration [J]. Chinese Journal of Computational Mechanics, 2012, 29(2): 236-241.

Optimal sensor placement by using clustering method

ZHANG Heng, LI Shiqi, LIU Shiping, ZHANG Zhe, WANG Yue

(School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)

The match of experimental/theoretical models of complex structures is an important part in modal parameter modification. To measure and obtain the best information, a clustering optimal method for sensor placement was proposed. The method can effectively avoid the information redundancy when using a limited number of sensors. According to the dynamic similarity of the mode shape values in important modes, the DOFs were auto-clustered by usingk-means clustering algorithm. The effective independent method was used to search out the sensor locations with the highest modal resolution from each cluster. Finally, the numerical analyses on a cantilever beam and a cantilever plate and the modal test of a filter wheel assembly were carried out to verify the optimization method. The results show that the method can effectively select the independent sensitive locations with a much higher search efficiency.

sensor placement;k-means clustering; effective independent method; modal test; model validation

国家重大科技专项

2016-02-29 修改稿收到日期： 2016-05-30

张恒 男，博士生，1988年生

刘世平 男，博士，副教授，1971年生

TH113.1

A

10.13465/j.cnki.jvs.2017.14.009