基于稀疏带宽模态分解的变转速滚动轴承故障诊断

潘海洋， 郑近德,2， 童宝宏， 张良安,2

(1.安徽工业大学 机械工程学院，安徽 马鞍山 243032；2.马鞍山市安工大工业技术研究院工业机器人研究所，安徽 马鞍山 243000)

基于稀疏带宽模态分解的变转速滚动轴承故障诊断

潘海洋1， 郑近德1,2， 童宝宏1， 张良安1,2

(1.安徽工业大学 机械工程学院，安徽 马鞍山 243032；2.马鞍山市安工大工业技术研究院工业机器人研究所，安徽 马鞍山 243000)

针对以往信号处理方法存在的缺陷，提出了一种新的非平稳信号分析方法—稀疏带宽模态分解(Sparse bandwidth mode decomposition，SBMD).该方法将信号分解转化为约束变分问题，自适应地将信号分解为若干个IMF分量之和。另外，在变转速工况下，滚动轴承故障振动信号中含丰富的状态信息，将SBMD、阶次追踪分析和包络谱相结合应用于变转速工况条件下的滚动轴承故障诊断问题。实验分析结果表明，采用SBMD阶次包络谱方法可以及时有效的诊断变转速工况下的滚动轴承故障诊断问题。

稀疏带宽模态分解；阶次追踪分析；包络谱；滚动轴承；故障诊断

针对滚动轴承的故障诊断问题，已经有各种不同的故障诊断方法，但这些研究方法都是基于转速平稳状态下滚动轴承的故障诊断。然而在变速过程中，滚动轴承的振动信号往往包含了平稳运行时不易反映的状态特征，这些特征在变速情况下可能会被充分的表现出来[1]，因此，对变转速工况下的振动信号分析是非常有意义的。

在变转速工况下，滚动轴承振动信号往往是非平稳的，且故障特征频率成分会随转速的变化而变化，表现出随转速变化的调频特征，因此，不能直接将振动信号视为平稳信号进行频谱分析，否则会发生“频率模糊”的现象[2]。阶次跟踪分析技术可以将时域的非稳态信号通过衡定的角增加重采样变成角域平稳信号，能够提取信号中与参考轴转速有关的信息，同时对与转速无关的信号进行抑制[3]，重采样信号有利于对变转速工况下的滚动轴承振动信号进行状态分析。

当轴承发生故障时，其振动信号常会表现为多分量的调幅-调频特性。要对这类信号进行分析，首先需要对振动信号进行解调。目前应用最广泛的自适应信号处理方法有：经验模态分解(Empirical Mode Decomposition，EMD)[4-5]、局部均值分解(Local Mean Decomposition，LMD)[6]、局部特征尺度分解(Local Characteristic Scale Decomposition，LCD)[7]，但是上述方法或多或少存在一些自身的缺陷[8-10]。另外，EMD、LMD和LCD方法都是采用包络分析方法或者插值方法完成信号的分解，由于信号极值点分布的毫无规律性，使得采用包络或者插值方法避免不了会产生端点效应、频率混淆等问题，而这些问题难以从根本上解决。

鉴于以往信号处理方法的缺点，Dragomiretskiy等在维纳滤波模型的基础上提出了变分模态分解(Variational Mode Decomposition，VMD)方法[11]，该方法是将信号分解转化为约束变分问题，自适应地将信号分解为若干个IMF分量之和，本质上区别于以往的信号处理方法。但是，VMD 方法中需要预先人为设定分解模态个数、初始中心频率和二次惩罚项参数等，分量个数和二次惩罚项参数对分解结果有很大影响，其中最为重要的是该方法并没有一个标准来衡量分解的结果。因此，本文在VMD的基础上，提出一种新的时频分析方法——稀疏带宽模态分解(Sparse Bandwidth Mode Decomposition，SBMD)方法。该方法首先预设参数的最大值；然后结合正交性及循环迭代的方法寻求最优参数，以单分量信号带宽最小优化目标进行优化，将复杂信号分解为若干个内禀模态函数(Intrinsic Mode Function，IMF)之和；最后对各个单分量信号进行解调得到对应的瞬时频率和瞬时幅值，从而获得原始信号完整的时频分布。因此，对SBMD方法进行研究有助于开拓时频分析方法的新思路，并且具有重要的理论意义。

综上所述，本文通过阶次跟踪分析获得平稳信号，结合SBMD和包络分析方法，提出了一种基于阶次跟踪和SBMD包络分析的变转速滚动轴承故障诊断方法。即首先采用阶次跟踪分析对变转速滚动轴承故障振动信号进行角域重采样，将时域非平稳信号转换为角域平稳信号；然后通过SBMD方法对角域信号进行分解，得到若干IMF分量；最后对包含主要故障信息的IMF分量进行包络阶次分析，从而对不同工作状态和故障类别下的滚动轴承进行识别。

1 SBMD方法

SBMD方法的目标是将一个实信号自适应地分解为若干个IMF分量之和，这里我们希望这种分解满足一定的分量条件。

假设uk(t)是一个调幅-调频的信号，其方程表达式为

uk(t)=Ak(t)cos(φk(t))

(1)

SBMD算法抛弃传统的循环剥离逐个获取各个分量的方法，其本质是将信号分解过程转移到变分框架内，通过寻求约束变分模型的最优解进行信号的自适应性分解，以及在搜寻过程中优化K值及二次惩罚项参数α，采用分量之间的正交性为判据确定参数值，其中，在循环迭代求解模型时，不断更新每个IMF的频率中心和带宽，根据信号表现出来的频率特性最终可以完成信号带宽的自适应分解，得到准确的窄带IMF分量。

由于实际情况中的K值及其他参数不得而知，预先设置的K值仅仅是个初始值，代表最大分解的数量，其初始值设置越大，其结果越准确，但时间越长，因此设定K值时，根据实际情况比预计的分量个数略大即可。然后采用循环迭代方法寻求真实分量个数及其他参数，同时以分量正交性最小为判据，即：

(2)

通过循环优化，得出不同值下的正交性参数，由于理想分量之间的正交性越小越能表示分量完全分离开来，因此，采用循环优化迭代的方法，以分量间的正交性最小为判据选取分量的个数及其他有效参数。

在整个循环过程中，把分解转化成搜寻约束变分模型最优解的问题。假定将原始信号f通过寻优分解，得到K0个IMF分量，其对应的约束变分模型表达式如下

(3)

(4)

式中：{uk}={u1,…,wk}代表分解得到的K0个IMF分量；{wk}={w1,…,wk}表示IMF的频率中心。

为解决上述的最优解问题，引入增广Lagrange函数，即

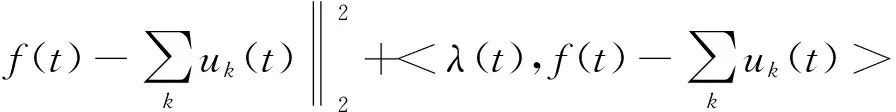
(5)

式中：α是惩罚参数；为Lagrange乘子。

将交替方向乘子算法应用于上述的增广Lagrange函数，可以求取函数的鞍点，也就是模型的最优解，这时就把原始信号f分解为K0个窄带IMF分量。

具体步骤如下：

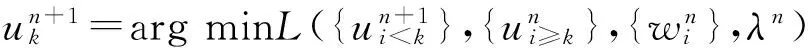
(6)令α=α+r(r为步长)，直至α=A(A为设置的最大α值)，结束内层第一个循环；

(7)令k=k+1，重复步骤(3)～(5)，直至k=K(K为设置的最大k值)，结束内层第二个循环；

(8)比较不同k值和α值下的正交性，选取正交性最小时所对应的k值和α值(假设k=K0,α=α0)，以及所对应的分量。

结束整个循环，输出结果，得到K0个窄带IMF分量。

2 仿真信号分析

分析式(6)所示的信号：

x(t)=2sin(60πt)×(1+0.5sin(2πt))+
sin(120πt)+cos(10πt)

(6)

x(t)是由三个分量组成，即调幅-调频分量、正弦分量和余弦分量，图1为仿真信号的时域图。为了验证SBMD方法的分解效果，分别选取常用的EMD和LCD进行对比。在采用三种方法对仿真信号分解之前，预先消除端点效应对分解结果的影响，抑制端点效应采用G Rilling 提出的镜像对称延拓方法[12]。

图1 仿真信号时域波形Fig.1 The time domain waveform of simulation signal

首先对仿真信号进行端点延拓，然后分别采用EMD、LCD和SBMD方法对延拓后的信号进行分解，可以得到不同的单分量，由于三种方法的原理不同，自适应分解出的分量个数也不同，分解结果如图2～图4所示。

图2 EMD分解结果Fig.2 The decomposition results of EMD

图3 LCD分解结果Fig.3 The decomposition results of LCD

图4 SBMD分解结果Fig.4 The decomposition results of SBMD

图2是EMD的分解结果， EMD方法采用极值点包络的方法获取分量信号，由于极值点分布的原因，致使分解的分量出现严重失真。图3是LCD的分解结果，LCD采用三次样条插值获取分量信号，三次样条插值在节点处具有二阶导数连续的特性，对于光滑信号或者平稳信号具有较好的效果，但是当信号表现出强非平稳特性时，该方法在包络特征曲线过程中会出现过包络和欠包络现象，致使分解结果失真。图4是SBMD的分解结果，SBMD 把信号分解的问题转变为约束优化的问题，以得到瞬时频率具有物理意义的调幅调频信号具有最小带宽为约束条件，并且以获取分量具有正交性为判据来自适应的优化选择分量个数，因此得到的分量没有出现失真。

下面再从时频域方面探讨几种方法的分解效果，图5～图7从时频域方面给出了三种方法的分量频率，判断在分解过程中是否出现“频率混淆”现象。原始信号中三个分量的频率分别为5 Hz、30 Hz和60 Hz，而图5和图6的分量出现明显的“频率混淆”现象，EMD和LCD方法得到的谱图出现较大失真，使相应的频谱图失去了原有的物理意义，无法准确地反映出原信号的瞬时幅值和随时间变化的频率规律；SBMD得到的频谱图很好地反映了原信号的基本信息，分量频率完全正确。因此，SBMD分解方法和其它方法相比具有明显的优越性。

图5 EMD分解得到的时频谱Fig. 5 The time-frequency spectrum with EMD

图6 LCD分解得到的时频谱Fig. 6 The time-frequency spectrum with LCD

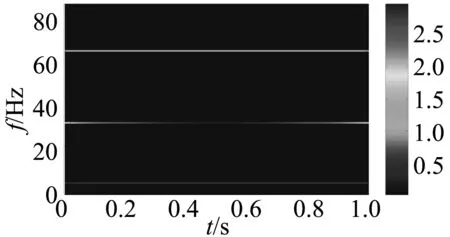
图7 SBMD分解得到的时频谱Fig. 7 The time-frequency spectrum with SBMD

3 基于SBMD阶次包络谱的变转速滚动轴承诊断方法

当滚动轴承处于变转速工况下，其振动信号往往表现为多载波多调制特性，且信号的故障特征频率成分随着轴转速变化而变化。文中将阶次跟踪分析、包络谱和SBMD相结合来识别变转速工况下的滚动轴承故障类型。基本步骤如下：

(1)对滚动轴承振动信号和转速信号以采样率fs采样，得到等时间间隔的采样信号。对滚动轴承正常、内圈故障和外圈故障三种状态进行采样，每种状态采集N组样本。

(2)对所有样本通过基准转速信号计算等角度增量Δθ所对应的时间序列ti。

(3)根据时间序列ti的值，对振动信号进行插值，求出其对应的幅值，将信号转化为角域平稳信号。

(4)利用SBMD方法首先对各个角域信号样本进行分解，每个样本分解得到若干个IMF单分量。对每一个样本的前i个IMF分量进行包络阶次分析，通过包络特征来确定滚动轴承的工作状态和故障类型。

4 实例分析

为了验证本文所提方法的可行性，试验中采用的滚动轴承型号为6307E型深沟球轴承，振动信号由轴承座上的加速度传感器采集，同时由转速传感器获得基准转速。试验设置了外圈局部损伤和内圈局部损伤两种故障，分别是通过激光在内圈和外圈上开槽来模拟裂纹故障。通过计算，滚动轴承的外圈和内外圈故障特征阶次分别为x0=3.04和xi=4.95。在实验台上，分别进行滚动轴承外圈、内圈局部损伤，以及正常三种工况下的瞬态实验。实验时采样频率为8 192 Hz，采样时间为20 s。图8是由实验测得的外圈故障下的滚动轴承振动加速度信号x(t)，图9是振动信号对应的基准转速信号，可以看出信号历经了由加速到减速的过程，而图8中的振动加速度信号的幅值也呈现了相一致的变化。由于信号是随转速变化的，如果直接进行包络谱分析，会出现“频率模糊”的现象。不失一般性的截取4～6 s的升速过程信号x1(t)，对x1(t)进行阶次跟踪分析，将信号由时域重采样变化为等角增量的角域信号x0(θ)，图10是阶次重采样后的信号波形，此时信号横坐标已经变为弧度。

进行角域重采样过后，接着进行SBMD分解，由于该方法采用分量正交性作为判据分解信号，因此避免了人为因素的干扰，选择合适的分量个数和α值，其分解结果如图11所示，结果包含三个分量和趋势项。然后对前三个分量求包络谱，其包络结果如图12～14所示。

图8 外圈故障滚动轴承振动信号时域波形Fig. 8 The time domain waveform of vibration signal of roller bearing with out-race fault

图9 外圈故障滚动轴承基准转速信号Fig.9 The speed signal of roller bearing with out-race fault

图10 阶次追踪分析后的角域信号波形Fig.10 The angular domain waveform after order tracking analysis

图11 SBMD分解的角域信号IMF分量结果Fig.11 The resulted IMFs of angular domain signal by SBMD

图12 第一个IMF分量的阶次包络谱Fig.12 Order envelope spectrum of the first IMF

图13 第二个IMF分量的阶次包络谱Fig.13 Order envelope spectrum of the second IMF

图14 第三个IMF分量的阶次包络谱Fig.14 Order envelope spectrum of the third IMF

可以看出，图12和图14中在外圈故障特征阶次的1倍处有明显的谱线，图13中在外圈故障特征阶次x0=3.04的1、2、3倍处有明显的谱线，都说明了滚动轴承外圈存在局部故障，与实际情况相符。由于噪声信号和干扰成分的存在，使得特征频率出现少许偏差，以及不在故障特征处也出现了少许峰值。

下面对滚动轴承内圈故障进行分析，图15是内圈故障滚动轴承振动信号时域波形图，其阶次跟踪分析后的SBMD分解图如图16所示，从图中可知，信号的主要信息主要集中在第2、第3和第4个分量。因此对这几个分量进行包络分析。其分析结果如图17～图19。从图17～图19中可以看出，在阶次O=4.95处有清晰的谱线，对应1倍内圈故障特征阶次，在阶次O=1及倍频处也有清晰的谱线，则对应着转频阶次。因此对变转速工况下的内圈故障信号进行包络阶次分析可以很好地判别故障类型。

图16 SBMD分解的内圈故障角域信号IMF分量结果Fig.16 The resulted IMFs of angular domain signal by SBMD

图17 第二个IMF分量的阶次包络谱Fig.17 Order envelope spectrum of the second IMF

图18 第三个IMF分量的阶次包络谱Fig.18 Order envelope spectrum of the third IMF

图19 第四个IMF分量的阶次包络谱Fig.19 Order envelope spectrum of the forth IMF

综上所述，将SBMD和阶次跟踪分析相结合应用于变转速工况下的轴承故障诊断，实验结果表明，此方法可以有效准确地识别故障状态，从而有望为旋转机械故障诊断提供一种新的识别分析方法。

5 结 论

机械设备运行时，其变转速信号往往包含了平稳信号所不能反映的特征，本文结合变速下滚动轴承振动信号的特性，将SBMD阶次包络谱应用于变转速工况下滚动轴承的故障诊断中，经研究得出以下结论：

(1)与EMD、LCD等传统信号处理方法相比，SBMD方法将信号处理问题转变为约束优化的问题，以得到瞬时频率具有物理意义的调幅调频信号具有最小带宽为约束条件，同时引入正交性作为判据，得到更加真实的IMF分量。

(2)采用阶次跟踪分析将时域的非稳态信号通过衡定的角增加重采样变成角域平稳信号，能够提取信号中与参考轴转速有关的信息，同时对与转速无关的信号进行抑制。

[1] 李志农,丁启全,吴昭同,等.旋转机械升降速过程的双谱-FHMM识别方法 [J]. 振动工程学报,2003, 16(2):171-174. LI Zhinong, DING Qiquan, WU Zhaotong ,et al. Study on bispectrum-FHMM recognition method in speed-up and speed-down process of rotating machinery [J]. Journal of Vibration Engineering, 2003, 16(2):171-174.

[2] 康海英,栾军英,郑海起,等.基于阶次跟踪和经验模态分解的滚动轴承包络解调分析[J].机械工程学报,2007, 43(8):119-122. KANG Haiying, LUAN Junying, ZHENG Haiqi, et al. Envelope demodulation analysis of bearing based on order tracking and empirical mode decomposition [J]. Chinese Journal of Mechanical Engineering, 2007, 43(8): 119-122.

[3] WU J D , WANG Y H, CHIANG P H, et al. A study of fault diagnosis in a scooter using adaptive order tracking technique and neural network [J]. Expert Systems with Applications, 2009, 36(1): 49-56.

[4] WANG H C, CHEN J, DONG G M. Feature extraction of rolling bearing’s early weak fault based on EEMD and tunable Q-factor wavelet transform [J]. Mechanical Systems and Signal Processing, 2014, 48, (1/2): 103-119.

[5] FENG Z P, LIANG M, CHU F L. Recent advances in time-frequency analysis methods for machinery fault diagnosis: a review with application examples [J]. Mechanical Systems and Signal Processing, 2013, 38(1): 165-205.

[6] JONATHAN S S. The local mean decomposition and its application to EEG perception data [J]. Journal of the Royal Society Interface, 2005, 2(5): 443-454.

[7] 程军圣,郑近德,杨宇.一种新的非平稳信号分析方法——局部特征尺度分解[J].振动工程学报, 2012, 25(2):215-220. CHENG Junsheng, ZHENG Jinde, YANG Yu. A non-stationary signal analysis approach—the local characteristic-scale decomposition method [J]. Journal of Vibration Engineering, 2012, 25(2): 215-222.

[8] HOU T Y, Z. HI Z Q. Adaptive data analysis via sparse time-frequency representation [J]. Advances in Adaptive Data Analysis, 2011, 3(1/2):1-28.

[9] LI C, LIANG M. A generalized synchrosqueezing transform for enhancing signal time-frequency representation [J]. Signal Processing, 2012, 92: 2264-2274.

[10] 郑近德,程军圣,杨宇. 部分集成局部特征尺度分解:一种新的基于噪声辅助的数据分析方法[J]. 电子学报, 2013, 41(5): 1030-1035. ZHENG Jinde, CHENG Junsheng, YANG Yu. Partly ensemble local characteristic-scale decomposition: a new noise assisted data analysis method [J]. Acta Electronica Sinica, 2013, 41(5): 1030-1035.

[11] DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition [J]. IEEE Transactions on Signal Processing, 2014, 62(3):531 - 544.

[12] RILLING G, FLANDRIN P, GONCALVES P. On empirical mode decomposition and its algorithms [C]∥ Proceedings of IEEE- EURASIP Workshop on Nonlinear Signal and Image Processing NSIP-03. Grado, Italy, 2003.

Fault diagnosis approach for roller bearings based on the sparse bandwidth mode decomposition under variable speed conditions

PAN Haiyang1, ZHENG Jinde1,2, TONG Baohong1, ZHANG Liang’an1,2

(1. School of Mechanical Engineering, Anhui University of Technology, Ma’anshan 243032, China;2. Institute of Industrial Robots, Ma’anshan Anhui University of Industrial Technology Research Institute，Ma’anshan 243000, China)

In view of the defect of previous signal processing methods, a new non-stationary signal analysis method, namely, the sparse bandwidth mode decomposition (SBMD) was proposed. The essence of the method is that the signal decomposition is converted into a constrained variational problem, and the signal is decomposed into a set of IMFs by SBMD. In addition, the vibration signals of roller bearings with variable speed usually contain more comprehensive status information, so, the SBMD combined with the order tracking and envelope spectrum analysis is suitable for applying in the fault diagnosis of roller bearings under the working condition of variable speed. The experimental results validate that the approach can handle the variable speed roller bearing fault diagnosis accurately and effectively.

sparse bandwidth mode decomposition; order tracking analysis; envelope spectrum; roller bearing; fault diagnosis；

国家自然科学基金(51505002); 安徽高校自然科学研究项目资助(2015A080)

2016-02-25 修改稿收到日期： 2016-05-30

潘海洋 男，硕士，助教，1989年5月生

郑近德 男，博士，讲师，1986年3月生

E-mail：lqdlzheng@126.com

TH113

A

10.13465/j.cnki.jvs.2017.14.014