流固耦合的多层搅拌反应器振动特性研究

胡效东， 王 灏， 王世飞， 张景坡， 曾庆良

(山东科技大学 机械电子工程学院，山东 青岛 266590)

流固耦合的多层搅拌反应器振动特性研究

胡效东， 王 灏， 王世飞， 张景坡， 曾庆良

(山东科技大学 机械电子工程学院，山东 青岛 266590)

针对某型号搅拌反应器搅拌主轴因振动断裂的问题，基于流固耦合理论，采用CFD和FEM相结合的单向耦合稳态的数值模拟以及经验公式计算方法。在考虑流场作用的条件下分析多种方法得出搅拌器的临界转速结果。分析主轴断裂的原因及影响搅拌器的固有频率的流体因素，并对主轴结构进行改进。得出结论：主轴驱动电机转速大于主轴的最低设计转速是主轴产生振动断裂的主要原因；搅拌介质的流体力和阻尼作用对搅拌器的固有频率均有影响；可以将主轴适当加粗以提高其临界转速，从而远离共振范围并有效解决振动问题；采用流固耦合的方法能够考虑搅拌器转动、流体载荷和搅拌桨叶的影响。其计算结果比经验公式更接近实际情况。

搅拌反应器；流固耦合；临界转速；CFD

搅拌反应器是化工、石油、食品、医药等行业的关键设备之一。在搅拌、混合、分离等多种工艺生产中具有重要作用。其功能的实现主要依靠于搅拌转子的转动。所以对搅拌反应器的振动特性和稳定性具有较高的技术要求，对实际中的搅拌反应器的振动特性进行研究具有重要意义。

模态分析则是进行一切较为复杂的动力特性分析的前提和基础。为了得到系统较为准确的动力特性分析结果，必须首先得到符合实际情况的系统的模态分析结果。转子模态问题一直备受国内外学者的关注。徐斌[1]基于流固耦合理论，采用 SIMPLEC 算法分析斜流泵叶轮的强度，确定了叶轮最大变形位置是在叶片外缘处。高红斌等[2]分析单级悬臂泵轴-电机系统的动态响应，建立的集中质量力学模型和扭转振动方程，可以方便、快捷地求出 IS 型单级单吸式离心泵主轴的固有频率、临界转速和主振型。刘厚林等[3]采用双向和单向的流固耦合方法分析了导叶式离心泵的强度，以单向流固耦合技术分析了离心泵的强度。荆丰梅等[4]在潮汐水轮机的研究中采用实验法验证了单向顺序耦合的可靠性。黄文俊等[5]采用有限元法计算风机转子的临界转速。潘旭等[6]对高速转子桨叶结构的轴流泵的叶片进行振动分析。

本文针对某化工企业的搅拌反应器主轴因振动过大而断裂问题。基于流固耦合理论，采用 CFD 方法模拟搅拌反应器内部的流体特性，对搅拌反应器进行应力分析，并计算流固耦合作用下搅拌反应器的多阶固有频率，并对比分析搅拌介质的流体力和阻尼作用计算临界转速。结合相关的经验公式计算结果，探讨主轴断裂原因及改进措施。

1 动力学方程及分析

对于搅拌反应器这样一个振动系统，可以假设其系统总共具有n个自由度，则可以得出其系统的振动方程为

(1)

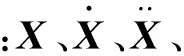
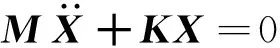
(2)

在考虑水对转子的影响时，考虑流体波动方程并离散化见式(3)。

(3)

结合式(1)可得式(4)。

(4)

式中：p为流体声学压力，M为质量矩阵，C为阻尼矩阵，K为刚度矩阵，F为应力矩阵，Ff为流体附加激振力矩阵，Kr为离心应力刚度矩阵，Mf为流体等效质量矩阵，ρf为流体密度，R为流固耦合矩阵，Kr为离心应力刚度矩阵，Kf为流体附加刚度矩阵[7-8]。

在假设系统处于自由振动时，系统运动方程式(2)的解如式(5)

Xi=A(i)sin(ωnit+φi)

(5)

对于振动系统，式(5)中振幅A(i)必有非零解，则必有式(6)。

(6)

2 搅拌反应器的模型建立

2.1 搅拌器模型的建立

搅拌反应器包括传动装置、搅拌釜体、搅拌主轴搅拌桨叶。转子模型可参考为单轴承约束的悬臂梁模型，如图1所示。搅拌轴直径D=120 mm，上层四宽叶旋桨搅拌器直径DJ3= 850 mm；叶片宽度h3=340 mm，中层离心式搅拌器直径DJ2=800 mm，下层四宽叶旋桨搅拌器直径DJ1= 800 mm；叶片宽度h1=320 mm。上层、下层桨叶厚度均为10 mm，中层桨叶厚度为5 mm。搅拌轴总长L=3 140 mm，反应釜内径D2=2 600 mm。反应釜直边s=3 185 mm，反应釜上下封头均为标准椭圆封头。

图1 反应釜整体搅拌结构图Fig.1 The structure of the stirred-tank reactor

搅拌轴与搅拌器的材料为不锈钢S30408，密度ρs=7 930 kg/m3，弹性模量E=200 Gpa，泊松比v=0.285。搅拌物料密度ρ=1 000 kg/m3。工况转速为n=220 r/min。因只研究搅拌反应器在工况下的动力特性，主要考虑流固耦合作用，故简化搅拌系统模型，流体区域建模如图2所示。

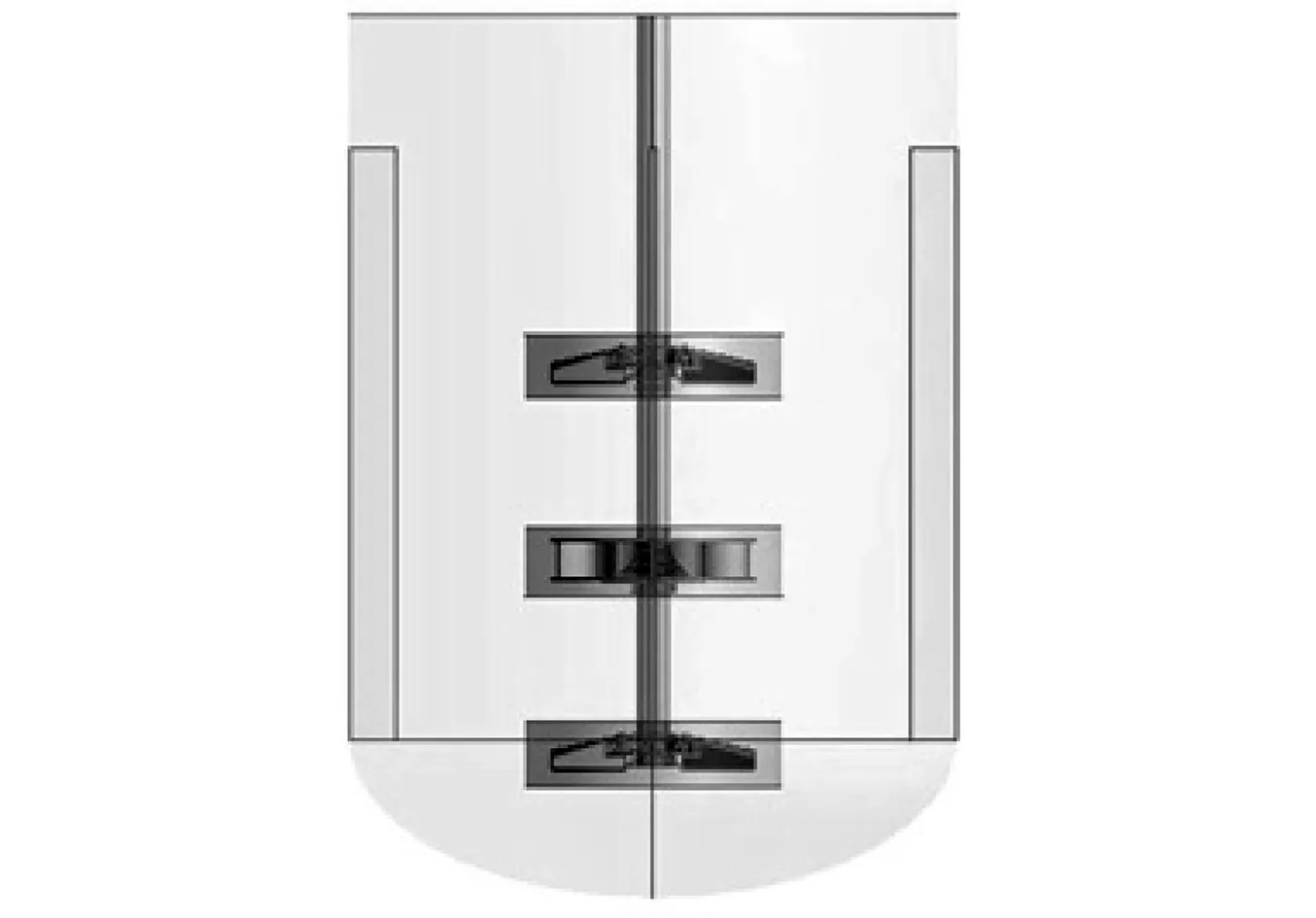
图2 搅拌反应器示意图Fig.2 The mixing model of the rotor-mediumagitator reaction

2.2 网格划分

搅拌反应器流体区域的网格划分如图3。整个流体区域体积较大，采取分块划分网格方法。流体区域网格总单元数为760 244，总节点数为647 719，如图3所示。固体结构网格单元总数为28 119，节点数为92 478，网格划分情况如图4。

图3 流体域网格划分示意图 Fig.3 The grid diagram of fluid

图4 固体域网格划分示意图Fig.4 The grid diagram of solid

3 基于流固耦合搅拌反应器应力分析

3.1 搅拌反应器流场模拟计算

由文献[8-10]可知，搅拌转子在实际工况中，所受载荷是处于非定常的。因此受到载荷波动的影响，转子的固有频率值会围绕一恒定值波动变化，但是工况载荷数值的变化范围较小，且其波动周期与转子的转动周期有关。因此将搅拌转子视为处于稳态流场的作用下，采用单向耦合的方法。选择标准k-ε湍流模型，将动区域的速度与轴面速度统一设置为工况转速，模型设定为稳态求解。最后进行迭代运算，导出流场对搅拌反应器的应力值，其流场模拟情况如图5。

3.2 搅拌反应器静应力分析

将流场分析结果导入静应力分析模块，对搅拌反应器的模型施加约束和载荷。载荷包括搅拌反应器的自身重力，搅拌反应器在工况旋转速度下产生的旋转预应力，流场在搅拌过程中产生的流体力。约束包括搅拌轴末端的圆柱约束。因轴承和轴封的非线性影响不适合于后期线性模态分析方法，而且模型中的搅拌反应器属于单支撑悬臂梁模型，与传统的转子动力学的双轴承模型有较大差别。因此简化为圆柱约束，忽略轴承的阻尼和刚度对系统的影响。对流场模拟结果进行分析并导入至搅拌反应器的对应面上如图6。

图5 流场流速矢量图Fig.5 The velocity vector of fluid

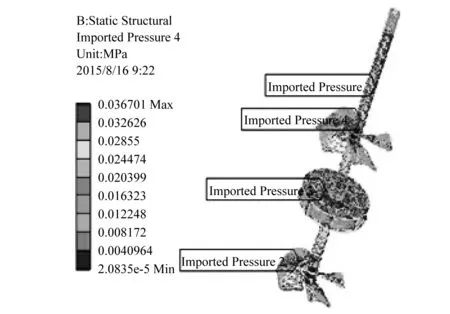
图6 耦合面压力Fig.6 The stress of coupling surface

最后将设置求解总应变和总应力，对搅拌反应器进行受力分析。等效应力云图如图7所示，应变量如图8所示。由图7和图8可知，搅拌桨叶在桨叶根部和桨叶末端受力较大。原因是在搅拌过程中，桨叶作为直接的搅拌装置带动流体运动，故流体对桨叶的反作用力较大。由于较薄的搅拌桨叶变形积累，在桨叶末端变形较大。并且中层搅拌结构类似离心泵结构，导致流体受力出现明显的质心偏移，与文献[10-11]相符。

桨叶与搅拌轴的固定方式为圆柱形约束，这使搅拌轴所受到的横向力主要来源于桨叶的受力变形。搅拌轴的应力云图表明，整个搅拌轴的受力变化较为均匀，无明显应力突变或应力集中，应力最大值不足以导致搅拌轴的断裂。所以可以排除因应力过大导致搅拌轴失效的原因。因此，考虑搅拌轴的断裂与搅拌器的振动特性有关，可能会由于工况转速过于接近其共振频率产生过大的振动。

图7 等效应力云图 Fig.7 Equivalent stress nephogram

4 搅拌反应器的临界转速计算

4.1 有限元法的临界转速计算

4.1.1 自由状态下的临界转速计算

首先对转子做自由振动状态的模态分析，仅对转子模型施加相应的约束。采用 ANSYS 模态分析中的线性 Block Lanczos 算法，搅拌转子在不考虑预应力和介质阻尼(自由振动)前10阶的固有频率如表1。由模拟结果可知，仅前5阶段振型如下：第1阶的振型为沿x轴的摆动；第2阶的振型为沿z轴的摆动；第3阶的振型为沿x轴的扭动；第4阶的振型为沿z轴的扭动；第5阶的振型为沿y轴的扭转。叶片叶轮的变形量与距离轴线的远近有关，距离轴线越远，变形量越大，呈对称分布。

图8 应变量图Fig.8 Deformation

模态12345频率/Hz5.3135.31635.4735.4837.22模态678910频率/Hz62.7562.8362.9263.0772.18

4.1.2 考虑预应力状态下的临界转速计算

搅拌转子的固有频率是转子自身的属性，主要由转子的质量矩阵和结构刚度矩阵决定。而刚度矩阵会受应力作用而变化。因此以流场模拟的应力计算结果作为模态分析的边界条件。并且施加相应的工况载荷如工况转速下产生的自身旋转预应力，自身的重力。求解计算后可以得到无阻尼有预应力条件下转子的前10阶固有频率和振型，如表2。

因模型为低速转子，受电机和工艺要求的影响，高阶固有频率所转化的临界转速对实际工况的研究意义不大。因此根据实际情况对计算结果进行筛选，计算所得的一阶临界转速(可由相应的一阶固有频率转化)具有参考价值。由表2可知f2=4.55 Hz。只考虑预应力的转子模态分析表明：除第3，4，5阶以外，其他阶固有频率均有下降。且随着阶数的升高，预应力降低效果越不明显，从第1阶的14.3%到第10阶的3%。因此在计算该低速转子模型中的一阶临界转速时，预应力对临近转速的计算影响较大。

表2 流固耦合作用下搅拌反应器前十阶固有频率

4.1.3 考虑搅拌介质阻尼作用下的临界转速计算

考虑到实际工况中搅拌转子处于流体介质的影响，其流固耦合作用较复杂。流体介质对转子的影响也体现在对转子的阻尼作用。因此结合实际中的搅拌介质范围，默认介质为不可压缩无粘度的理想介质。建立搅拌介质-搅拌转子模型。并通过插入命令的方式实现对搅拌介质边界条件的施加，即所谓的湿模态计算。为研究数值模拟中干湿模态对搅拌转子的临界转速影响，以有无流体介质的阻尼作用作为差别条件进行对比模拟，可得表3。

表3 阻尼作用下搅拌反应器前十阶固有频率

由表可知，搅拌转子在搅拌介质的阻尼作用下，各阶固有频率均有明显的下降。由其是高阶固有频率受搅拌介质的影响较大，前10阶的固有频率均有明显的下降。从第1阶的7.7%到第10阶的33.28%，搅拌转子的固有频率明显降低。与文献[12]中的结果相符合。但该搅拌转子模型是低速搅拌转子，由于实际工况要求的限制，同样取有效计算结果即第一阶临界转速，即第一阶固有频率f3=4.9 Hz。由此可知，在分析该搅拌转子的低阶临界转速时，临界转速受阻尼影响较低。但在分析高阶的临界转速时，流体介质的阻尼作用对高阶临界转速影响较大。

4.2 经验公式法的临界转速计算

根据《搅拌与混合设备设计选用手册》中搅拌轴设计可得出搅拌轴的临界点转速。通常把工作转速n低于第一阶临界转速ncr的轴称为刚性轴，给定的实际工作转速为220 r/min，低于仿真分析的第一阶临界转速273 r/min。这里按照刚性轴进行计算分析。公式中仅考虑了搅拌介质的附加质量从而求出搅拌轴的第一临界转速ncr31=306.4 r/min，而在不考虑预应力(当流体默认为无黏性不可压缩的理想流体时，流体作用可适用于附加质量计算[13])的数值模拟中得出临界转速为ncr0=294.6 r/min。对比理论计算和有限元法仿真分析得到的临界转速可看出，两种方法得到的结果相差较小为2.87%。从而在理论上验证了有限元法的可靠性，但是比较湿模态与有预应力的模态计算结果以及经验公式计算结果，三者仍有一定差值。但计算结果最小值(即为nmin≤0.7ncr=191 r/min)仍低于工况转速(即n=220 r/min)，即工况转速恒处于共振转速区间，则可知是由于搅拌主轴的结构不合理，临界振动频率比较接近电机的驱动频率，振动过大降低主轴的使用寿命，从而过早失效。转子的低阶固有频率受搅拌过程产生的预应力和搅拌介质的阻尼作用共同影响。由于本模型中转子属于低速转子，临界转速多为一阶固有频率的转化结果。对比计算结果可知，采用流固耦合计算预应力的方法可以满足计算需求。

5 优化改进

由模拟计算和经验理论公式计算结果可知，实际工况转速处于搅拌反应器的共振转速区间内，易发生共振问题。调节搅拌轴的轴径能够改变主轴的临界转速。将搅拌反应器的轴径由120 mm扩大至150 mm。采用数值模拟的计算方法得到搅拌器的固有频率如表4所示。

由表4可得f4=6.0 Hz，临界转速ncr4=60×f=360 r/min。该主轴相应的临界转速为n4≤0.7ncr4=252 r/min。

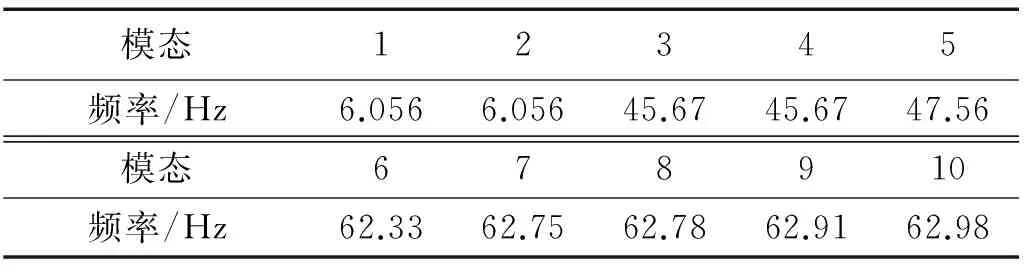
表4 优化后搅拌反应器前十阶固有频率

再由经验理论公式计算优化后的搅拌轴的第一临界转速为ncr5=379.25 r/min，响应的主轴驱动频率最高为n5=265.48 r/min。两者结果相接近。均远高于220 r/min的工况转速。则优化设计后的搅拌主轴振动较低，运转工况良好。

6 结 论

(1)采用数值模拟计算该搅拌反应器的动力特性，搅拌转子在流场中的受力分布具有对称分布的特点，最大应力出现在叶片与轮毂的结合处，在设计中应预防出现应力集中的现象。

(2)在通过数值模拟的计算转子的临界转速过程中，搅拌介质的流体力和阻尼作用对转子固有频率的影响明显。仅考虑预应力的临近转速计算为273 r/min，仅考虑搅拌介质的阻尼作用的仿真结果为297.6 r/min，相应的经验公式计算结果为306.4 r/min。相应的，后两种方法的计算结果基本一致，相差2.87%，且搅拌转子的预应力作用对于低阶固有频率影响作用较大，而搅拌介质的阻尼作用对高阶的固有频率影响作用较大。

(3)实际搅拌器驱动电机额定转速为220 r/min，转速高于搅拌器设计最低转速191 r/min，最终造成搅拌反应器搅拌轴振动过大，经过1年工作后产生断裂。通过增大搅拌主轴的轴颈，能够有效提高搅拌系统的临界转速，使之与驱动电机转速匹配，有效减小搅拌系统的振动，提高产品的使用寿命。在计算该反应釜的搅拌反应器的临界转速时，数值模拟方法充分考虑了流场对搅拌反应器的应力作用，及搅拌桨叶的影响，更能有效的得到搅拌器的实际振动特性。

[1] 徐斌. 混流式水轮机转轮流固耦合的动力特性分析[D]. 西安: 西安理工大学，2006.

参 考 文 献

[1] 赵振华，郝晓弘. 局部保持鉴别投影及其在人脸识别中的应用[J]. 电子与信息学报, 2013, 35(2):463-466.

ZHAO Zhenhua, HAO Xiaohong. Linear locality preserving and discriminating projection for face recognition[J]. Journal of Electronics & Information Technology, 2013, 35(2):463-466.

[2] 肖婷，汤宝平，秦毅，等. 基于流形学习和最小二乘支持向量机的滚动轴承退化趋势预测[J]. 振动与冲击, 2015, 34(9):149-153.

XIAO Ting, TANG Baoping, QIN Yi, et al. Degradation trend prediction of rolling bearing based on manifold learning and least squares support vector machine[J]. Journal of Vibration and Shock, 2015, 34(9), 149-153.

[3] HE X F, NIYOGI P. Locality preserving projections[C]// Neural Information Processing Systems16. Vancouver: MIT Press, 2004:153-160.

[4] ZHANG Zhenhua, ZHU Xinzhong, ZHAO Jianmin. Image retrieval based on PCA-LPP[C]// 2011 10th International Symposium on Distributed Computing and Applications to Business, Engineering and Science. Wuxi, China, 2011: 230-233.

[5] 王健，冯健，韩志艳. 基于流形学习的局部保持PCA算法在故障检测中的应用[J]. 控制与决策, 2013, 28(5):683-687.

WANG Jian, FENG Jian, HAN Zhiyan. Locally preserving PCA method based on manifold learning and its application in fault detection[J]. Control and Decision, 2013, 28(5):683-687.

[6] 张晓涛，唐力伟，王平，等. 基于多尺度正交PCA-LPP流形学习算法的故障特征增强方法[J]. 振动与冲击, 2015, 34(13):66-70.

ZHANG Xiaotao, TANG Liwei, WANG Ping, et al. Fault feature enhancement method based on multiscale orthogonal PCA-LPP manifold learning algorithm[J]. Journal of Vibration and Shock, 2015, 34(13):66-70.

[7] 杨庆，陈桂明，童兴民，等. 增量式局部切空间排列算法在滚动轴承故障诊断中的应用[J]. 机械工程学报, 2012, 48(5): 81-86.

YANG Qing, CHEN Guiming, TONG Xingmin, et al. Application of incremental local tangent space alignment algorithm to rolling bearings fault diagnosis[J]. Journal of Mechanical Eigineering, 2012, 48(5):81-86.

[8] JIA Peng, YIN Junsong, HUANG Xinsheng, et al. Incremental Laplacian eigenmaps by preserving adjacent information between data points[J]. Pattern Recognition Letters, 2009, 30(8):1457-1463.

[9] CHIN T J, SUTER D. Out-of-sample extrapolation of learned manifolds[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(9):1547-1556.

[10] 谈超，关佶红，周水庚. 基于等角映射的多样本增量流形学习算法[J]. 模式识别与人工智能, 2014, 27(2):127-133.

TAN Chao, GUAN Jihong, ZHOU Shuigeng. Multi-sample incremental manifold learning algorithm based on isogonal mapping[J].PR & AI, 2014, 27(2):127-133.

[11] 孙即祥. 现代模式识别[M]. 长沙：国防科技大学出版社，2002.

[12] YAN Shuicheng, XU Dong, ZHANG Benyu, et al. Graph embedding and extensions—A general framework for dimensionality reduction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(1):40-51.

Analysis on a multiple-impeller considering the fluid-structure interaction and its vibration characteristics

HU Xiaodong, WANG Hao, WANG Shifei, ZHANG Jingpo, ZENG Qingliang

(College of Mechanical and Electronic Engineering, Shandong University of Science and Technology, Qingdao 266590, China)

Aiming at analysing the damage mechanism of the stirring spindle of a certain type of mixing reactor due to vibration fault, based on the theory of fluid solid coupling, a numerical simulation, by using the combined method of CFD and FEM, on the one-way coupled stationary vibration was carried out and an empirical formula calculation was also conducted for comparison. Considering the effect of the flow field, the critical speed of the mixer was analyzed. The causes of the spindle fracture and the effect of the fluid factors on the natural frequency of the mixer was analyzed. On this basis, the structure of the spindle was improved. It is concluded that the motor speed, driving the spindle, greater than the minimum design spindle speed is the main reason of the vibration generating the main shaft fracture. The effect of the fluid force and damping on the natural frequency of the mixer is obvious. The enlargement of diameter can increase the critical speed, shift away from the resonance range and solve the vibration problem effectively. The method of analysing the fluid solid coupling can be used to investigate the influences of the rotation of the agitator, the load of the fluid and the mixing blades. The reults are more close to the actual situation than those by the empirical formula.

stirred reactor; fluid solid coupling; critical speed; computational fluid dynamics(CFD)

长江学者和创新团队发展计划(IRT1266 )；国家自然科学基金(51375282)；山东省自然科学基金(ZR2014EEM018)

2016-01-12 修改稿收到日期： 2016-05-31

胡效东 男，博士，副教授，1971年生

E-mail: huxdd@sohu.com

TB533+.1;TF351.5+2

A

10.13465/j.cnki.jvs.2017.14.021