浮力筒自由涡激运动的模型试验研究
2017-07-19康庄,李平
康 庄, 李 平
(哈尔滨工程大学 船舶工程学院,哈尔滨 150001)
浮力筒自由涡激运动的模型试验研究
康 庄, 李 平
(哈尔滨工程大学 船舶工程学院,哈尔滨 150001)
对外径150 mm,长700 mm垂直放置的浮力筒模型开展了自由涡激运动试验研究,测量了浮力筒在不同试验工况下六个自由度的运动参数,并着重对浮力筒顺流向、横向和艏摇运动的运动特性进行了分析。试验中发现,当约化速度较小时浮力筒主要发生顺流向运动而横向和艏摇运动较小且不规则;当约化速度增大到一定程度后,顺流向运动频率是横向运动频率的2倍,此时艏摇运动出现了两个主要运动频率,其中较大的艏摇运动频率等于横向运动频率,因此认为横向运动和艏摇运动的激励力来源相同,即二者存在耦合作用,而且浮力筒的运动轨迹呈现明显的“8”字形。试验中还发现,浮力筒涡激运动的平均拖曳力系数比圆柱绕流的阻力系数增大了约100%。
浮力筒;涡激运动;模型试验;“8”字形
流体流过物体后交替脱落的漩涡不仅会引起立管等细长圆柱体的涡激振动现象,对于类似Spar等大尺度海洋结构物的运动也会有影响。但这些大尺度结构的运动特征和立管的涡激振动现象又有明显不同。为了与细长体的涡激振动现象作区分,通常将大型海洋结构由流体诱发的运动现象称为涡激运动(Vortex-Induced Motion,VIM)。
针对涡激运动现象,模型试验研究是一种有效的研究方法,国外的许多学者用该方法开展了较多的研究工作。Govardhan等[1]对球形结构的VIM现象进行了试验研究,他们通过改变球形结构的质量比和系泊绳索的长度,发现圆球的运动轨迹呈“8”字形,而且涡激运动幅值Amax/D可达到1左右;此外,横向运动幅值几乎不受系泊绳长度的影响,而对质量比的变化更敏感。Irani等[2]通过模型试验对Spar平台涡激运动现象进行了系统地研究,主要研究了尺度效应、质量比以及锚泊系统等参数对平台VIM的影响。Wilde等[3]对具有浮筒的自由站立式立管系统进行了涡激运动模型试验,研究了该系统在不同振动模态下的VIM响应。试验发现在一定的来流速度下,浮筒会产生艏摇运动(即旋转现象),但遗憾的是,他们的关注点更多的是浮筒顺流向和横向的平移运动,而没有对艏摇运动进行深入地研究。
虽然国内学者对涡激运动模型试验的研究起步较晚,但也取得了一定的成果。王颖等[4]对浮式圆柱进行了涡激运动模型试验,研究了流体对VIM的影响以及在流固耦合系统中柱体对流体的反作用。张蕙等[5]对Spar平台进行了模型试验,研究了侧板对平台运动轨迹的影响,以及流速和来流角对涡激运动平衡位置的影响。白治宁[6]通过CFD数值模拟与模型试验相结合的方法,对半潜平台模型的涡激运动响应特性进行了研究。试验发现半潜平台在流向角为135°以及Ur=7时,其运动幅值最大,此时平台的横向运动频率约等于固有运动频率。
目前关于涡激运动现象的研究多集中于实际工程中Spar等海洋平台的运动特性上,关于典型圆柱体的涡激运动机理的研究则相对较少,而且这些研究多集中在单自由度或者双自由度的涡激运动现象上,对于圆柱体发生涡激运动时的艏摇现象的研究则非常少。因此,本文选取具有典型代表意义的圆柱形浮力筒,对其在不同试验工况下的涡激运动现象开展了模型试验。试验主要通过改变系缆绳长度和吃水位置来研究浮力筒顺流向、横向以及艏摇运动的运动特性,从而对圆柱形结构的涡激运动机理进行研究。
1 试验模型装置
试验在哈尔滨工程大学拖曳水池进行,该水池长108 m,宽7 m,水深3.5 m,并使用QUALISYS运动捕捉系统来测量数据,该系统主要通过测量三个光球的轨迹来分析浮力筒六个自由度的运动情况。
本试验的浮力筒模型采用玻璃钢制作,整体呈刚性,分为四个舱室,并严格要求加工工艺,确保浮力筒的重心位于几何中心处。浮力筒模型的示意图如图1所示,模型外径及重量如表1所示。
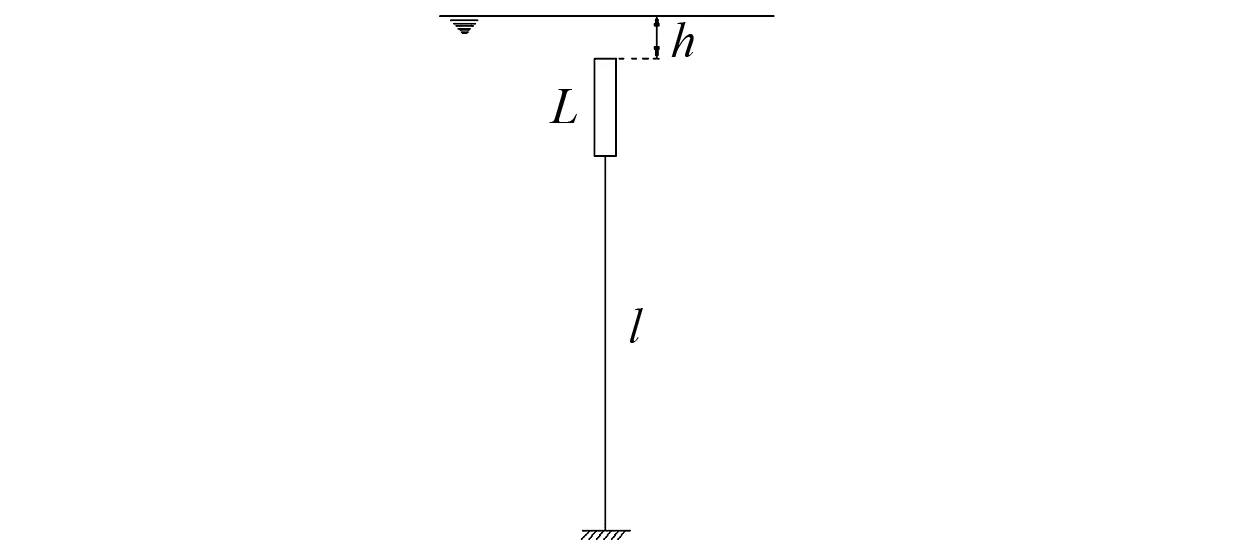
图1 浮力筒示意图Fig.1 Schematic diagram of the buoyancy can
其中,h为浮力筒顶部距水面的距离,L为浮力筒的长度,l为浮力筒的系泊绳长度。
浮力筒的拖曳状态如图2所示,沿圆柱体轴线上方安装了一个轻质铁丝架,该铁丝架上固定了三个高度和角度各不相同的光球,Qualisys运动捕捉系统通过捕捉三个光球的运动轨迹来测量浮力筒六个自由度的运动参数。

表1 浮力筒参数
在本试验中,为了测量浮力筒的艏摇运动,主要通过细绳把浮筒底部圆心和沉入水中的铁框相连。使用细绳连接的目的:为了不对艏摇运动产生影响,即降低了旋转阻尼的作用,而且绳索在两端张力的作用下,不会出现弯曲现象,细绳始终处于拉紧状态,即细绳的伸缩变形很小可以忽略不计,可视为刚性绳。铁框通过四根等长度绳索连接固定到拖车上,拖车运行时可通过绳索调节浮筒顶部与水面位置关系。进行试验时还需要在铁框中装上压载块,以便维持铁框的稳定性,这样保证了Qualisys系统测量到的浮力筒涡激运动数据准确可靠。

图2 浮力筒拖曳状态Fig.2 Dragging state of the buoyancy can
2 试验工况
本次研究中,定义水流方向为顺流向(In-Line Direction),垂直于水流方向为横向(Cross-Flow Direction),最小流速为0.1 m/s,最大流速为0.42 m/s,流速间隔0.01 m/s。(在处理数据时,本文对锁定区内的无量纲频率比f*取流速间隔为0.01 m/s的点作图,即进行加密处理,而对其它图则按流速间隔为0.02 m/s取点作图。)
浮力筒VIM模型试验的工况设置如下:首先保持系缆绳长度不变,改变浮筒顶部距水面的距离,分别测量浮力筒在不同流速下的六自由度运动。然后保持浮力筒顶端距水面距离固定不变,依次减小浮力筒的系缆绳长度,并再次测量不同流速下的浮力筒的六自由度运动。其工况的详细信息如表2所示。
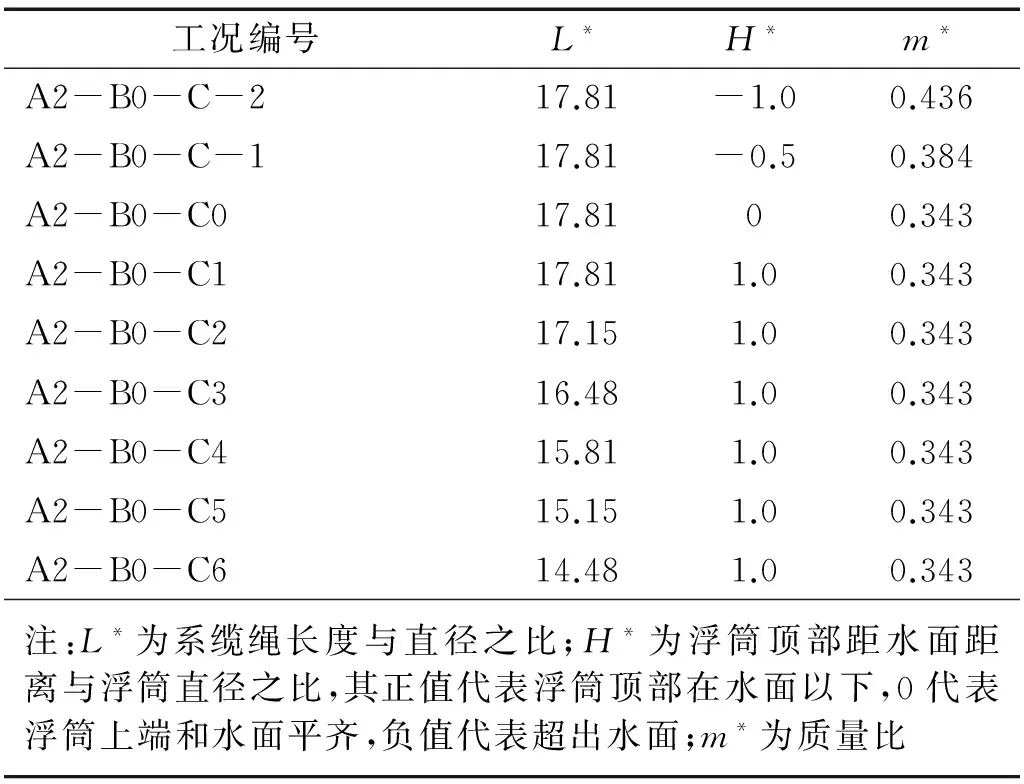
表2 浮力筒的试验工况
3 参数定义
在本次试验中,约化速度(又称为折合速度)Ur的定义如下
(1)
斯特劳哈尔数St和雷诺数Re的定义如下
(2)
(3)
本试验雷诺数的变化范围取在亚临界阶段,即1.5×104≤Re<6.3×104。
浮力筒的振动幅值以无量纲运动均方根幅值的形式给出,定义如下
(4)
折合频率,即频率比:浮力筒涡激运动的横向振荡频率fy与其在静水中的固有频率fn的比值如下。
(5)
式(1)~(5)中:U为来流速度;D为浮筒外径;fn为浮力筒固有频率;f取漩涡泄放频率;ν为流体运动黏性系数;xi为浮筒运动位移测量值;μ为顺流向或横向位移均值,fy为横向振荡频率。
4 试验数据处理
4.1 静水条件下浮力筒横荡固有频率结果分析
浮力筒纵荡和横荡在静水条件下的自由衰减频率相同,故只做了浮力筒横荡的静水自由衰减试验,为求得更加准确的横荡固有频率,每个工况做了3~4次静水自由衰减试验,从而求得横荡的固有频率和周期。表3为浮力筒各试验工况下的横荡固有频率。

表3 各试验工况下浮力筒横荡的固有频率
从表3可以看出,当浮力筒上端高出水面或与水面平齐时,横荡固有频率要小于浮力筒顶端没入水中的工况,而且高出水面的距离越大,其固有频率越小。如果把浮力筒静水自由衰减看作是倒立的钟摆,从理论上分析,横荡固有频率应随着系缆绳长度的减小而增大,而本试验的测量结果与理论能较好地吻合。
4.2 浮力筒涡激运动轨迹处理
本试验利用MATLAB软件提取浮力筒的稳定段试验数据,但受到试验条件的限制,测量所得到的浮力筒原始运动轨迹并不理想,其光顺性和轨迹的重合度较差。为了抵消不利因素对试验的影响,本文采用傅里叶变换和系统识别法中的最小二乘法对浮力筒自由涡激运动顺流向和横向运动的轨迹进行了处理。
在本次模型试验的数据处理中,首先将浮力筒涡激运动的时间-位移曲线展开成5阶傅里叶级数形式,并把浮力筒涡激运动顺流向(IL)和横向(CF)的展开基础频率均设为ω。浮力筒的运动位移的傅里叶级数展开式如下
(6)
式中,a0,0,ai,1,ai,2,b0,0,bi,1,bi,2和ω为相关系数。
在此基础上,采用最小二乘法进行分析计算。在本次分析中,根据最小二乘法,定义拟合参数f(a00,a11,a12,…,a51,a52),即:
(7)
式中:x为逼近函数拟合值;xi为试验中测量值。
分别对a00和aij值求偏导,其中i=0,1,2,3,4,5;j=1,2,并使它们的导函数等于零,求极值,从而求出a00,a11,…,a51,a52的值,得到xc(t)。同理,对于函数yc(t)应用此方法。结果发现a1,1≈0,a1,2≈0,这表明浮力筒涡激运动中顺流向的运动频率为2ω,是横向运动频率的2倍,这符合圆柱形浮力筒自由涡激运动频率的特性,也与常规涡激振动的“8”字形轨迹是吻合的[7]。
图3为浮力筒涡激运动原始数据和经系统识别法处理后的数据,从图中可看到拟合函数和原始运动曲线拟合度较高。图4为圆柱形浮力筒的涡激运动轨迹,从图中可发现浮力筒重心的运动轨迹为“8”字形,而且经系统识别法处理后,涡激运动轨迹的光顺度和重复性明显提高。
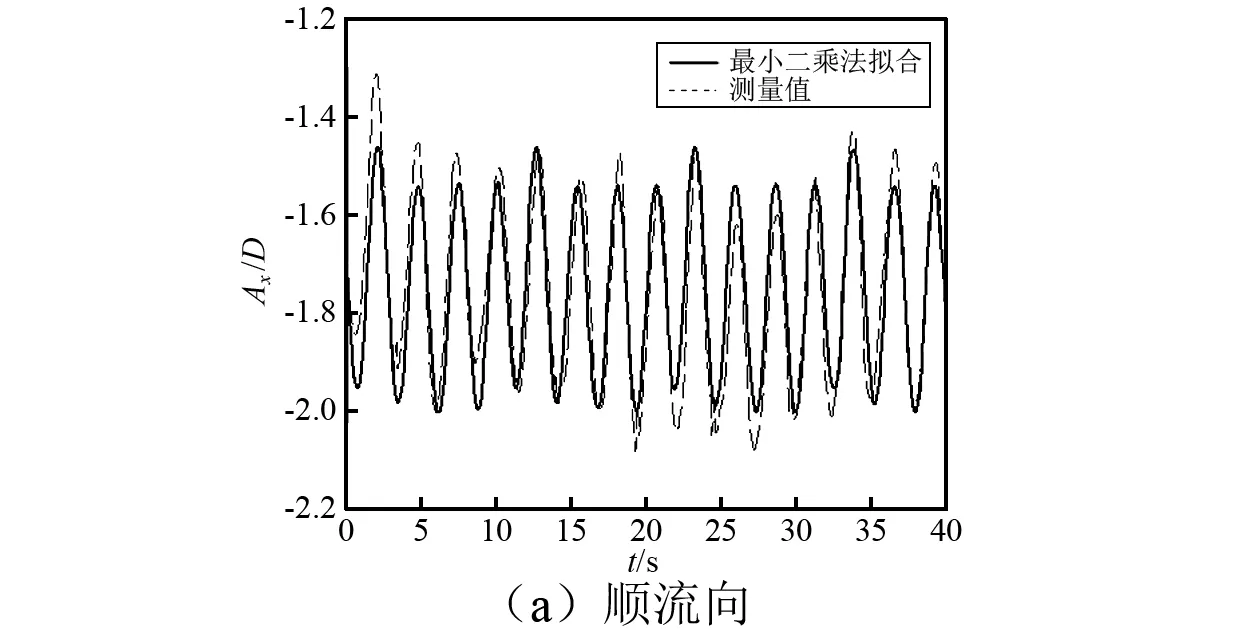
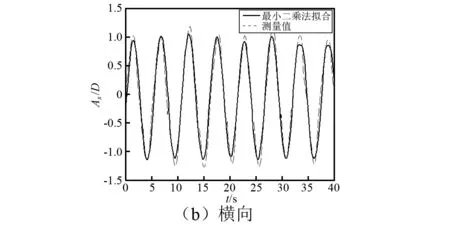
图3 系统识别法处理前后的浮力筒涡激运动时间-位移曲线Fig.3 Time-displacement curve of the buoyancy can VIM by the method of system identification
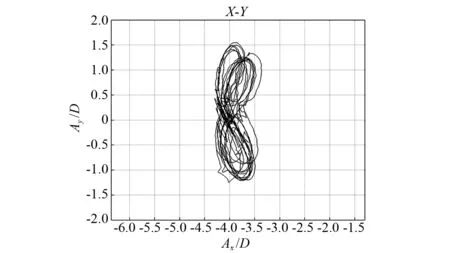
(a)涡激运动原始运动轨迹
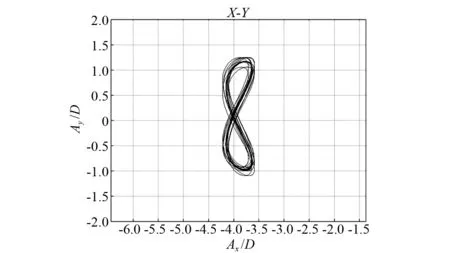
(b)系统识别法处理后的运动轨迹图4 浮力筒的涡激运动轨迹Fig.4 VIM trajectory of the buoyancy can
4.3 浮力筒涡激运动幅值和频率处理
首先使用MATLAB软件提取浮力筒的稳定段试验数据,并求出无量纲均方根振幅A*RMS。然后对试验数据进行谱分析,从而求得浮力筒顺流向、横向和艏摇运动所对应的频率。
5 浮力筒顺流向和横向运动特性分析
本试验中,浮力筒尺寸为Φ150×700 mm,L/D=4.67,试验流速为0.1~0.42 m/s。分别单独改变系缆绳长度和浮力筒顶端距水面距离,测量浮力筒在各流速下顺流向和横向的运动响应,所得结果如下。
5.1 浮力筒涡激运动轨迹结果分析
本文以工况fn=0.208 9 Hz,L*=17.81,H*=0,m*=0.343为例对浮力筒的运动规律进行分析。图5所示为浮力筒在部分约化速度下的时间—位移曲线,运动轨迹曲线以及顺流向和横向的功率谱密度曲线。图5中的CF(Cross-Flow)和IL(In-Line)分别代表横向和顺流向的振动方向;Ax和Ay则代表顺流向与横向的振动幅值。
试验发现,在约化速度较小时浮力筒顺流向和横向运动具有较大的随机性,而当约化速度增大到一定值后浮力筒两侧漩涡交替脱落频率变得稳定,横向和顺流向运动都较规则。此外,从图5还发现,顺流向运动频率是横向运动频率的2倍,而且浮力筒的运动轨迹呈明显的“8”字形,这与Spar平台的涡激运动轨迹是一致的。由于本试验没有减涡板等装置的干扰,因此浮力筒涡激运动的“8”字形要比Spar平台的轨迹更加规则且稳定得多。
同时,试验还发现多数工况下的“8”字形轨迹关于来流方向是非对称的。这可能是受到拖曳水池实验条件的限制或者其它如池壁和自由液面等因素的干扰,这些干扰因素共同导致了浮力筒自由涡激运动的轨迹关于来流非对称,也是涡激运动轨迹不光顺和重复性较差的主要原因。
作者曾进行过圆柱体双自由度涡激振动模型试验研究[8],试验中发现了多种不同形式的涡激振动轨迹,如“D”形、“卵”形和“雨滴”形等,总结得到圆柱体涡激振动的运动轨迹由“雨滴”形至“8”字形的演变历程,即:“雨滴”形尖端产生闭合圈闭合圈不断变大 “8”字形。文中认为振动固有频率比与流速是出现不同振动轨迹的主要原因。在本试验中发现浮力筒涡激运动的轨迹也成“8”字形,但没有出现“D”形、“卵”形和“雨滴”等形状。
5.2 浮力筒运动频率与幅值结果分析
从图5的运动频率图可知,当Ur较小时,横向运动较不稳定,而且还出现了多个运动频率。随着Ur的增大,浮力筒横向运动的轨迹也逐渐变得规则,当Ur>3.36后,浮力筒横向运动只有一个主频。而浮力筒顺流向运动在多个约化速度下均出现了“多频”现象,其中就包括顺流向运动频率等于两倍横向运动频率的现象,同时还出现了其它的低频分量。

图5 浮力筒时间-位移曲线和相应的运动轨迹及频率(部分约化速度下)Fig.5 Time-displacement curve & motion trajectory& frequency of the buoyancy can
图6给出了浮力筒尾流的无量纲频率f*随着约化速度Ur增加的变化情况,同时图中还给出了Khalak等[9]试验结果。
从图6可以看出:当约化速度介于2.80~4.48时,涡泄频率随着约化速度的增大而增大;当涡泄频率接近浮筒的固有频率时,涡泄频率会锁定在柱体的固有频率上并在一定约化速度范围内始终约等于柱体的固有频率,在这个约化速度范围内(约为5~7.5)圆柱的涡激运动处于锁定状态;当约化速度进一步增大时,涡泄频率又开始增大,相应地浮筒运动脱离锁定状态。从图中还可以看出,虽然部分测量点与参考文献的测量结果有一定的偏差,但是本试验与 Govardhan和Khalak的试验结果在整体趋势上能较好地吻合。
图7为圆柱绕流的斯特劳哈尔数随雷诺数的变化趋势[10],图8则给出了浮力筒涡激运动的斯特劳哈尔数随约化速度的变化趋势。表4为浮力筒涡激运动模型的锁定参数(包括初始锁定的约化速度Ur)及斯托哈尔数的计算结果同Stappenbelt等[11]实验值的对比。
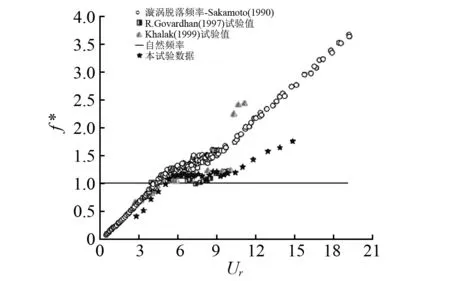
图6 无量纲频率f*与约化速度Ur关系图Fig.6 The relationship between f* and Ur

表4 锁定参数及斯特劳哈尔数

图7 斯特劳哈尔数随雷诺数的变化图Fig.7 The change of Strouhal number with Re

图8 浮力筒横向涡激运动的斯特劳哈尔数Fig.8 St number of the buoyancy can in-line VIM
由图7可知,当300≤Re<3×105时,圆柱体发生涡激振动时横向振动频率的St数基本保持恒定,约为0.2,而在雷诺数其它区间的St数则没有确定的数值。在本次研究中,雷诺数的变化范围为1.5×104~6.3×104,但浮力筒横向涡激运动频率所对应的St数与之差距较大,结果可如图8所示。
由图8可知,当约化速度小于3.92时,St数随约化速度的增大而增大;当约化速度大于3.92时,St数稳定在0.125附近。结果表明,浮力筒发生涡激运动时的St数比圆柱绕流的St数(约为0.2)要小。
图9和图10分别给出了各工况下浮力筒顺流向和横向涡激运动的均方根幅值结果。由图9可以看出各试验工况下顺流向运动幅值随约化速度的变化规律基本相似。在约化速度小于5时,顺流向运动的均方根幅值随着约化速度的增大而迅速从约0.05增大到约0.22。当约化速度介于5~13.33时,顺流向运动的均方根幅值保持在较高水平,最大均方根幅值达到了0.3。当H*等于-1和0时出现了类似“双峰”的现象。在约化速度介于5.7~6.4时出现了一个峰值,随后在约化速度达到8.5时达到了另一个峰值,幅值大小约为0.25,其中第二个峰值所在的约化速度范围较大。

图9 浮力筒各工况下顺流向运动均方根幅值Fig.9 RMS of in-line direction in various working conditions of the buoyancy can
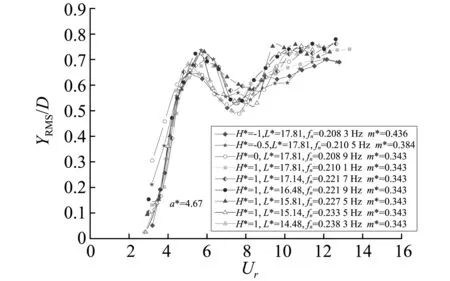
图10 浮力筒各工况横向运动均方根幅值Fig.10 RMS of cross-flow direction in various working conditions of the buoyancy can
从图10则可发现,浮力筒的横向涡激运动出现了明显的“双峰”现象,而且横向运动幅值随约化速度的变化趋势基本相同。当Ur介于2.8~5时横向运动幅值迅速增大,当Ur≈5.3时出现了第一个峰值,均方根幅值约等于0.73;然后横向运动幅值随约化速度的增大而降低;当Ur≈7.5时均方根幅值达到最小,此时其值约为0.5;此后横向运动均方根幅值随约化速度增大而增大,当Ur达到10左右时均方根幅值达到第二个峰值,其值约为0.76,两个峰值大小几乎相等;当Ur>10以后横向运动幅值稳定在0.76左右。
图11为Govardhan球体涡激运动试验中的横向运动均方根幅值。通过对比图10和图11发现浮力筒和圆球的横向运动具有类似现象。在圆球试验中,随着约化速度的变化,横向运动均方根幅值先后出现了两个峰值,且当约化速度大于10以后,幅值稳定在第二个峰值。本文的浮力筒横向运动幅值与文献的参考值能够较好地吻合,不同之处在于本试验的两个峰值几乎相等,而圆球试验中的两个峰值相差约80%。在圆球试验中还发现质量比相等时,系泊线长度和约化速度的改变对横流向运动幅值的变化趋势几乎没有影响。

●以及○ 分别代表L*等于8.93和3.83图11 Govardhan VIM试验的横向运动均方根幅值Fig.11 RMS of the cross-flow direction in Govarhan’s VIM model test
在本试验中,当质量比等于0.343、系泊线长度与浮筒直径之比L*不相等且约化速度小于5时,不同的横向运动幅值曲线随着约化速度的变化而几乎是重合的。当约化速度大于5而值不相等时,横向运动幅值开始出现不同;当L*介于14.48~17.81之间而其值较小时,横向运动幅值反而较大。试验还发现,改变浮力筒顶端与水面之间距离对横向运动幅值影响不大。
6 浮力筒艏摇运动特性分析
试验发现,浮力筒的涡激运动与圆柱体的涡激振
动现象相比,增加了艏摇运动,即浮力筒绕垂向轴有一个往复的旋转运动。通过分析,作者认为当流体流经圆柱体发生边界层分离时会产生漩涡,即柱体下游的流体在逆压梯度作用下发生倒流,两股流体相汇的结果是回流流体把从上游来的流体“挤”出物面,使边界层内的流体进入流体深处,进而产生了剪切力。该剪切力会在水平面内产生一个的扭转力矩,在该力矩作用下浮力筒向一侧发生艏摇运动。当浮力筒另一侧发生漩涡脱落时,又产生了一个相反方向的扭转力矩,浮力筒艏摇运动减速,在某一点时速度降为0并开始向相反方向转动。Etienne等[12-13]通过数值模拟的方法,对圆柱体两自由度涡激运动(考虑圆柱体的旋转和横向运动)做了相关研究,分析了艏摇运动与横向运动之间的关系,认为艏摇运动是由涡激产生的,并将此现象称为涡激旋转(Vortex Induced Rotation,VIR)。同时还发现,当圆柱体的运动被限制在只有旋转一个自由度时,艏摇方向的运动幅值会随约化速度的增加而增大,并且在运动频率接近固有频率时艏摇幅值达到最大;当横向运动的自由度被释放时,艏摇的运动幅值会随之增大,而横向运动幅值反而会降低,即旋转运动会削弱横向运动,而横向运动会促进艏摇运动。鉴于此,本文认为圆柱体两侧漩涡的不对称交替泻放导致了浮力筒的艏摇运动,并且艏摇运动和横向运动的激励力来源是相同的,所以浮力筒艏摇运动与顺流向、横向运动存在着密切的关系。
试验中通过改变系缆绳长度和浮力筒顶端距水面距离,分别测量浮力筒在各流速下的艏摇运动响应。图12和图13示为工况取fn=0.208 9 Hz,L*=17.81,H*=0,m*=0.343,浮力筒在部分约化速度下的艏摇运动时间-位移曲线以及艏摇运动频率与固有频率、横向频率之比随约化速度的变化曲线。本文以该工况为例对艏摇运动响应规律进行说明。
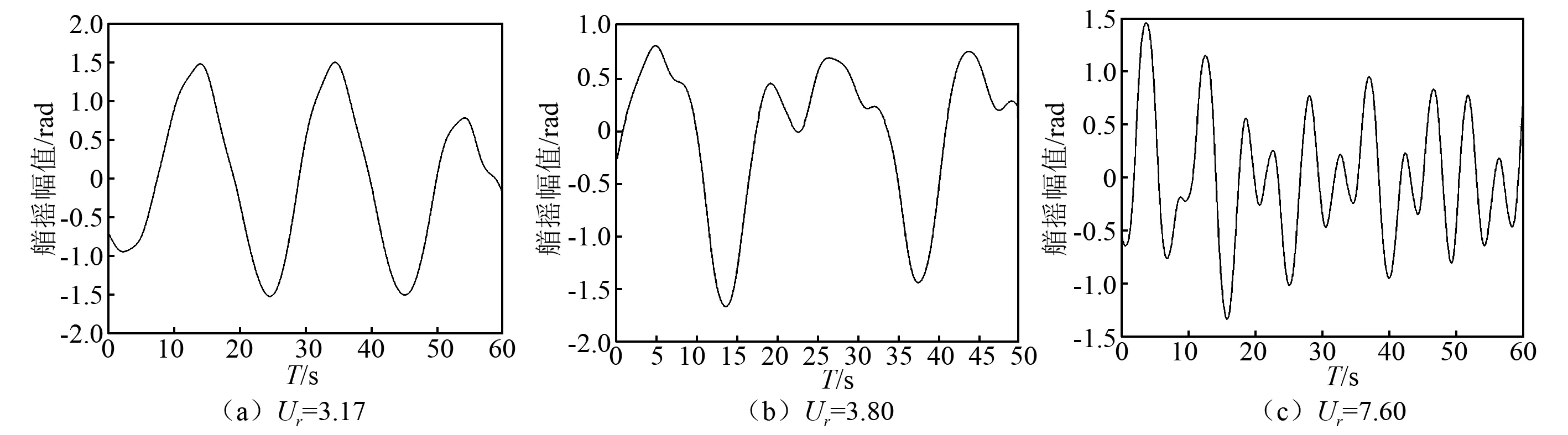
图12 浮力筒艏摇运动时历曲线(部分约化速度)Fig.12 Duration curve of yaw motion of the buoyancy can
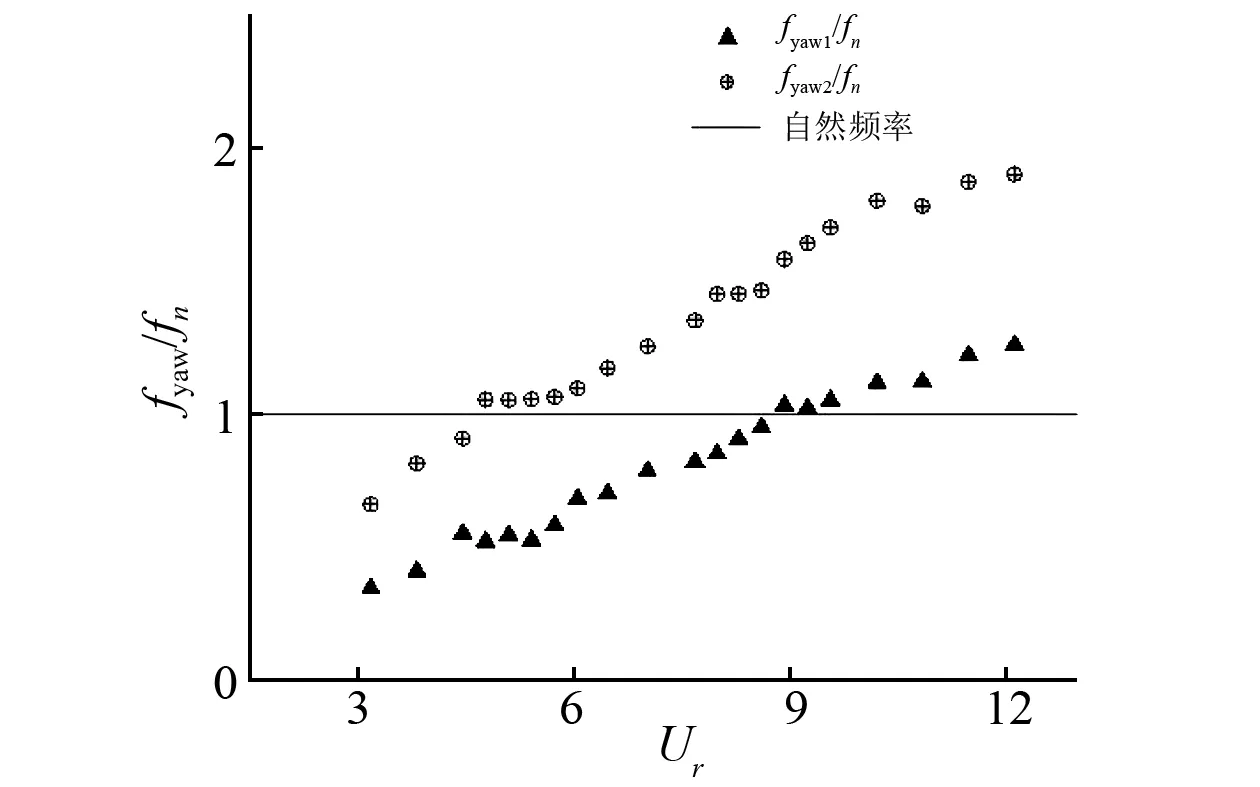
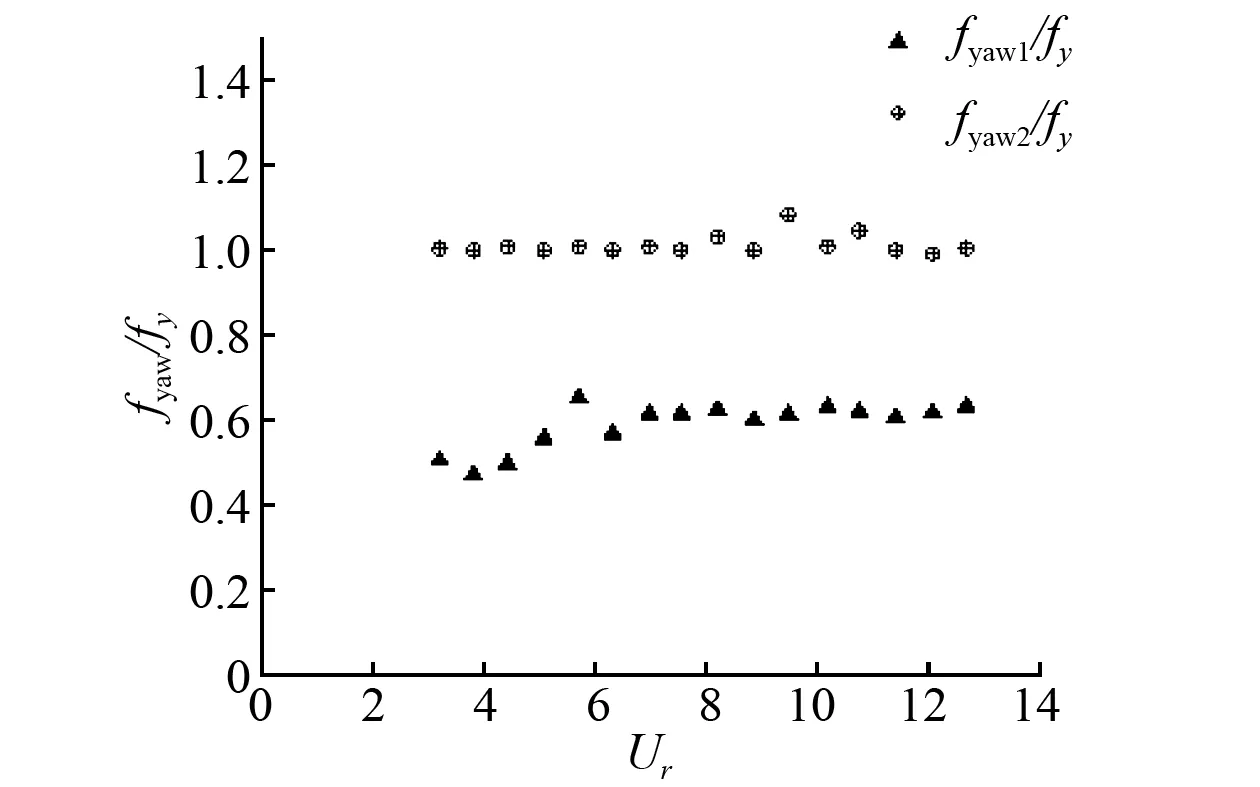
从图12的艏摇时历曲线可以看出浮力筒艏摇运动频率随约化速度增大的变化规律为,当Ur=3.17时浮力筒的艏摇运动频率是唯一的。当Ur>3.80时,浮力筒艏摇运动出现了两个主要运动频率,即存在两个主要的运动模态,分别记为fyaw1和fyaw2,这两个艏摇运动频率均随约化速度变化而几乎成线性增大。由图13(a)可以发现,当约化速度增大到一定程度时,艏摇运动频率fyaw2进入锁定区,使得旋转幅值迅速增大,而频率fyaw1会短暂进入锁定区,随后又快速脱离锁定区。同时,艏摇运动频率的总体增长趋势成“台阶”式增长。本文分析认为横向运动和艏摇运动的激励力来源相同,即二者存在耦合作用,因此将艏摇运动频率和横向运动频率作对比,结果如图13(b)所示。由上面的右图发现,较大的艏摇运动频率fyaw2和横向运动频率的比值约等于1,即两者取值相同,较小的艏摇运动频率fyaw1与横向运动频率的比值约等于0.62。
(a)
(b)图13 浮力筒艏摇运动频率与固有频率以及横向频率之比Fig.13 Ratio of yaw frequency and fn & fy of the BC
通过对浮力筒顺流向、横向和运动频率的分析,试验发现,当约化速度增大到一定程度后,顺流向运动主频是横向运动主频的2倍,而且横向运动主频等于较大的艏摇运动频率fyaw2。试验还发现,在有些工况下顺流向和横向运动同时出现了等于较小的艏摇运动频率的频率分量。
图14为浮力筒艏摇运动的斯特劳哈尔数,两个艏摇运动频率的St数分别记为St1和St2。试验发现,当约化速度分别等于3.8和4.43时St2较大,且随约化速度的增大而增大。当约化速度大于5.07后St2稳定在0.127附近。而当约化速度介于3.17~12.67之间时,斯特劳哈尔数St1稳定在0.078附近。
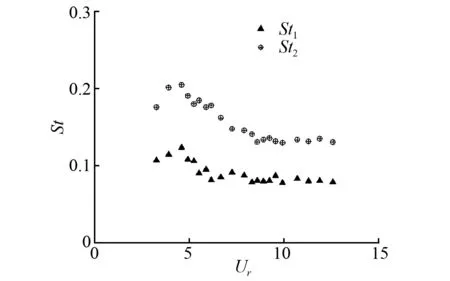
图14 浮力筒艏摇运动St数Fig.14 The St of the buoyancy can yaw motion
图15为浮力筒各试验工况下艏摇均方根幅值和最大幅值随约化速度变化,从图中可以发现浮力筒艏摇运动幅值随约化速度变化波动性较大。但各试验工况艏摇运动幅值总体变化趋势是相同的,试验中发现约化速度介于3.2~5.0时,艏摇运动均方根幅值随约化速度增大而迅速增大,约化速度大于5.0以后其均方根幅值在0.62 rad左右波动,最大运动幅值在1.3 rad左右波动。
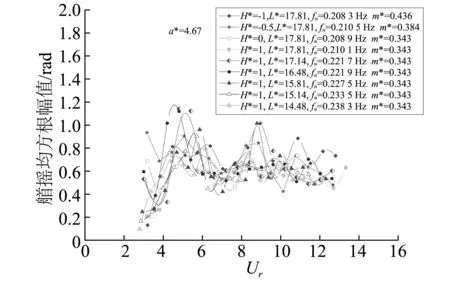
(a)浮力筒各工况艏摇均方根幅值
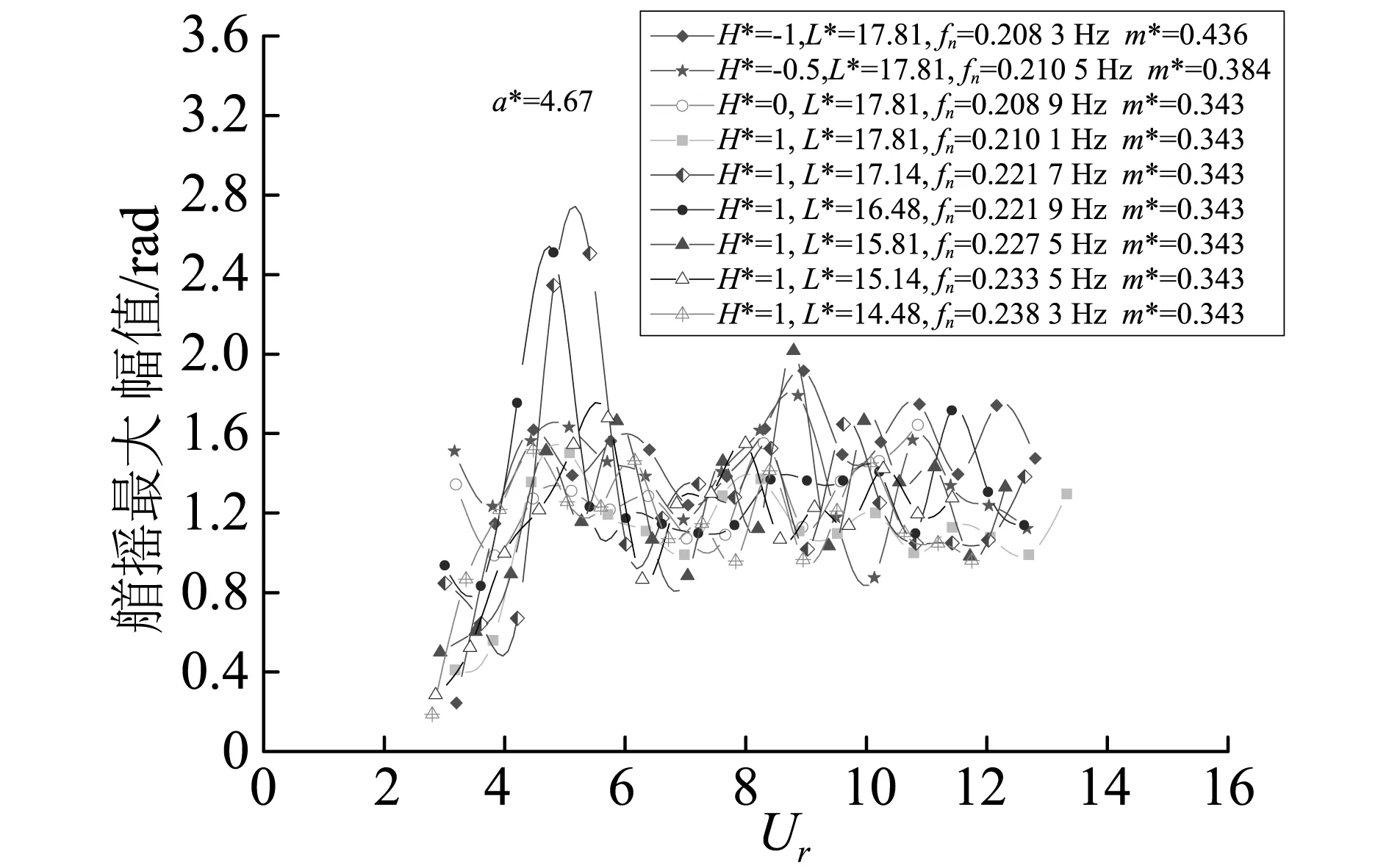
(b)浮力筒各工况艏摇最大幅值图15 浮力筒艏摇运动幅值Fig.15 Amplitude of yaw motion of the buoyancy can
综上,通过对浮力筒艏摇运动响应进行分析,试验发现:艏摇现象是贯穿整个涡激运动过程的,当约化速度较低时,艏摇运动频率是单频的而且随约化速度增大而增大;当艏摇运动开始出现两个频率,即“多频”现象,其中较大的艏摇运动频率等于横向运动频率。而且艏摇运动频率随约化速度增大呈“台阶”式线性增长。浮力筒艏摇运动幅值的波动性较大,但各工况下艏摇运动幅值随约化速度的整体变化趋势是相同的。试验还发现,系泊线长度和浮力筒顶端距水面的距离对艏摇运动幅值几乎无影响。
7 浮力筒涡激运动平均拖曳力系数分析
在浮力筒涡激运动试验中,浮力筒在来流U的作用下发生倾斜。对倾斜圆柱体进行受力分析,将来流分解为与浮力筒轴线垂直和平行的两个分量,分别记为Un和Ut,则来流对浮力筒的作用力可分解为法向分力Fn和切向分力Ft,如图16所示。
沿浮力筒法向分速度Un可用式(8)表示
Un=Ucosα
(8)
式中:α为U和Un之间的夹角。
在本试验中,切向方向的分力Ft不影响计算拖曳力系数CD,故忽略不计。沿法向方向分力Fn和法向速度Un存在如下关系
(9)
因此拖曳力系数CD可用下式表示
(10)
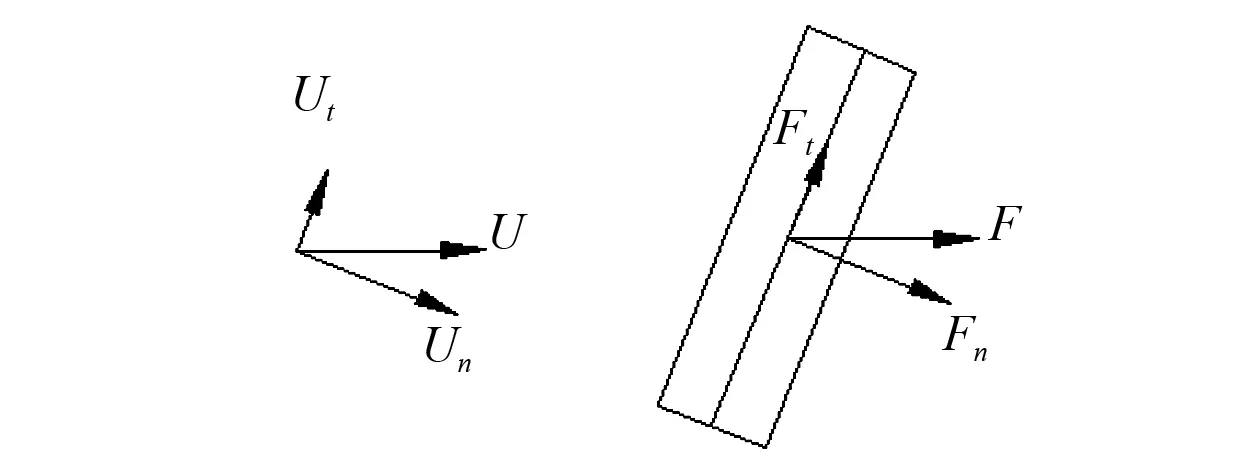
图16 倾斜圆柱体在均匀流中的受力分析Fig.16 Force analysis of the tilting cylinder in uniform flow
图17给出了浮力筒发生涡激运动时的受力分析,则浮力筒的法向方向分力Fn为:
Fn=(B-G)sinα
(11)
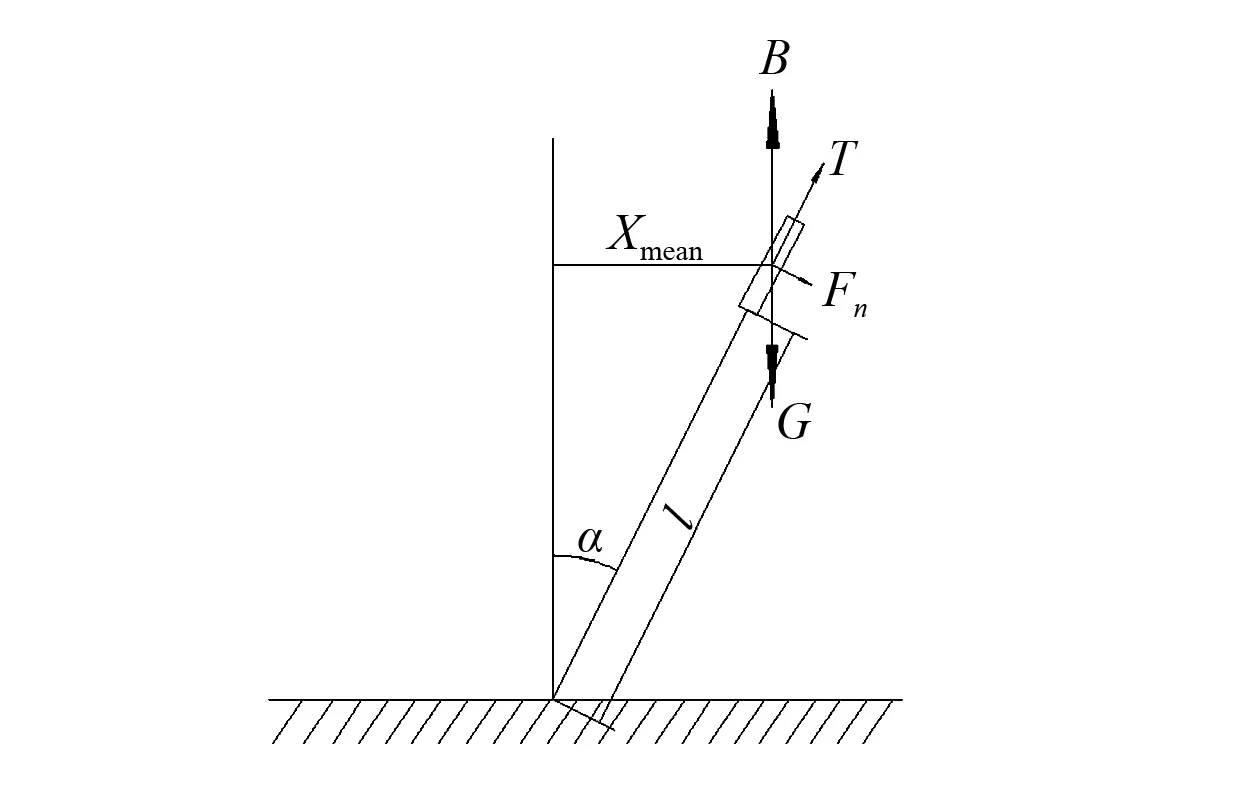
图17 浮力筒涡激运动受力分析Fig.17 VIM force analysis of the buoyancy can
(12)

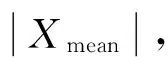
图18、19为平均拖曳力计算结果,图20、21为平均拖曳力系数计算结果。
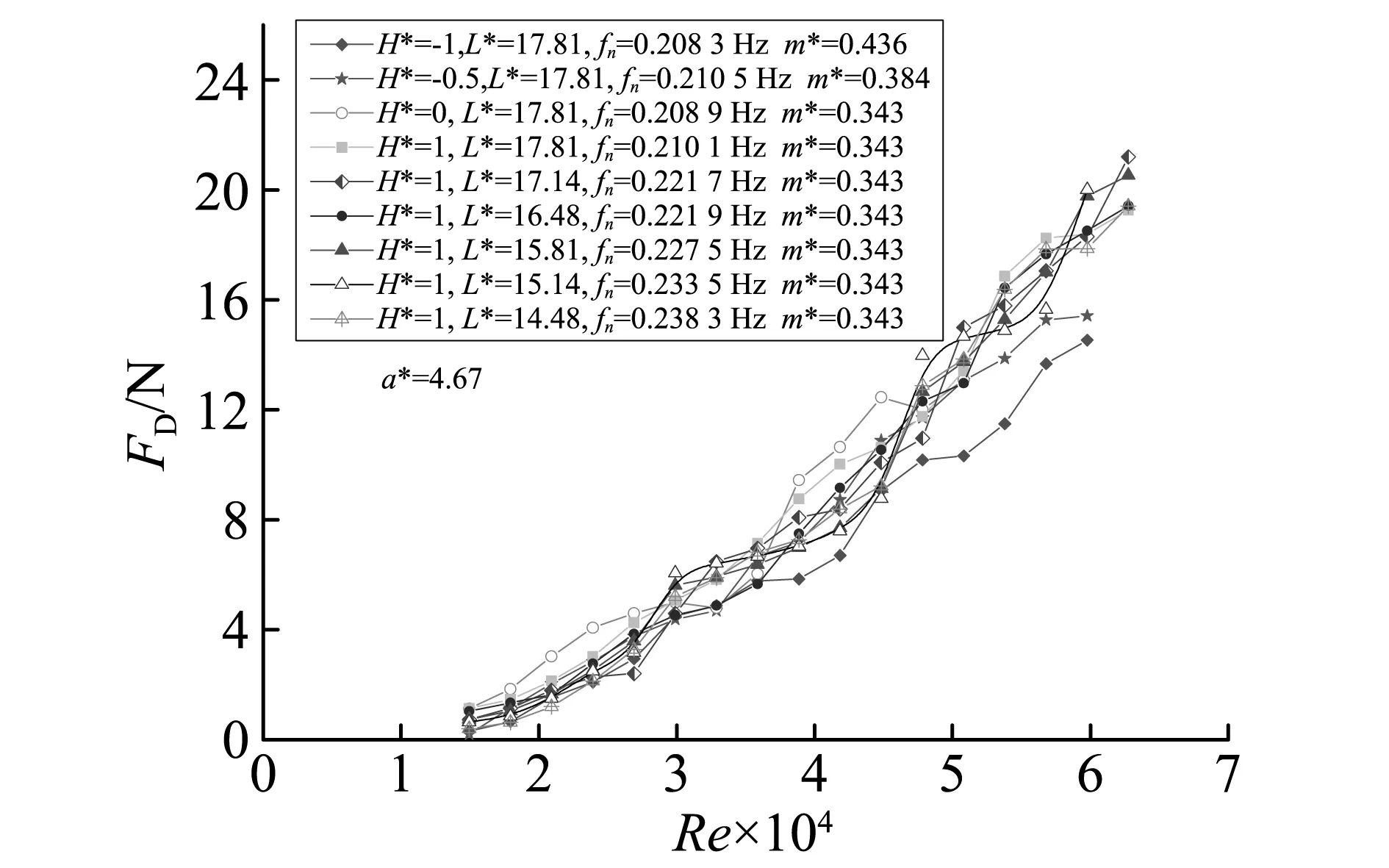
图18 浮力筒涡激运动平均拖曳力随Re变化Fig.18 Mean drag force of buoyancy can changes with Re
图19 浮力筒涡激运动平均拖曳力随Ur变化Fig.19 Mean drag force of buoyancy can changes with Ur

图20 浮力筒涡激运动平均拖曳力系数随Ur变化Fig.20 The CD of buoyancy can changes with Ur

图21 浮力筒涡激运动平均拖曳力系数随Re的变化趋势Fig.21 The CD of buoyancy can changes with Re
从图18~21可以看出,浮力筒平均拖曳力随着约化速度的改变,其整体变化趋势是基本相同的。当雷诺数介于1.4×104~2.6×104时,各工况下平均拖曳力系数CD均随雷诺数增大而增大,但在数值上则差别较大,这是因为流速较小时顺流向的运动不够稳定。从图中可以发现,拖曳力系数在雷诺数为2.6×104左右时达到峰值,当雷诺数大于2.6×104时,各工况下CD保持在较高值,随雷诺数增大虽有波动,但基本稳定在2.3左右。
从文献[10]可以发现,当雷诺数Re介于103~104时,圆柱绕流的阻力系数CD介于1.0~1.2,且随雷诺数的增大而略微增大;当雷诺数介于104~2.0×105时,阻力系数则基本保持不变,约等于1.2,该区间也是本试验雷诺数的变化区间。因此,本文发现圆柱形浮力筒发生涡激运动时的平均拖曳力系数远远大于圆柱绕流的阻力系数,其值比圆柱静止绕流阻力系数增大了约100%。
8 结 论
本文设计了一套垂直放置的浮力筒涡激运动模型试验装置,测量了不同工况下浮力筒六个自由度的运动参数,并重点分析了浮力筒顺流向、横向和艏摇运动的运动响应,所得结论如下:
(1)试验发现浮力筒发生VIM时会存在艏摇运动,即艏摇是贯穿整个涡激运动过程的,并且在锁定区的约化速度范围内能观察到明显的旋转现象。通过对艏摇运动特性进行分析,发现当Ur较小时艏摇运动频率是单一的,当Ur增大后艏摇运动开始出现两个频率,这两个运动频率均随Ur的增大而增大;把艏摇运动频率和顺流向及横向运动频率作对比,发现较大的艏摇运动频率等于横向运动频率,较小的艏摇频率与横向运动频率的比值约等于0.6,因此认为横向运动和艏摇运动存在耦合作用,从而致使旋转现象的出现。
(2)浮力筒艏摇运动幅值随约化速度的增大,其波动性的变化也较大,但总体来说浮力筒艏摇运动先随约化速度增大而增大,而后在波动中保持稳定。
(3)试验中发现浮力筒顺流向主运动频率为横向运动频率的2倍。其中当Ur较小时,浮力筒两侧漩涡脱落频率不稳定,横向频率也出现了多个频率分量;当Ur增大后运动较为稳定,此时横向运动只有一个主要频率,此时横向运动频率的St数约为0.125。
(4)浮力筒顺流向运动幅值先随Ur迅速增大,而后保持在较高水平,横向运动出现了“双峰”现象,且两个峰值大小几乎相当,当Ur>10以后横向运动幅值保持不变。试验还发现,系缆绳长度与浮筒直径之比L*对浮筒顺流向运动幅值影响不大,而Ur<5时对横流向运动幅值也几乎无影响,当Ur>5时系缆绳长度越小横流向运动幅值越大;浮筒顶部距水面距离与其直径之比H*对浮筒横流向运动幅值影响不大,当浮筒露出水面时顺流向幅值要大于顶端没入水中时。
(5)当Ur较小时浮力筒两侧漩涡对称脱落,浮力筒主要发生顺流向运动而横向运动较小且不规则,此时X-Y运动轨迹成扁平带状。随着Ur增大,浮力筒两侧漩涡开始交替脱落,浮力筒运动轨迹逐渐呈现明显的“8”字形。
(6)对浮力筒的平均拖曳力系数进行了计算,并与圆柱绕流的阻力系数作对比,发现圆柱形浮力筒发生涡激运动时的平均拖曳力系数比静止圆柱绕流的拖曳力系数增大了约100%。
[1] GOVARDHAN R, WILLIAMSON C H K. Vortex-induced motions of a tethered sphere[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 69/70/71:375-385.
[2] IRANI M, FINN L. Improved strake design for vortex induced motions of spar platforms[C]∥ Proceedings of the 24th International Conference on Offshore Mechanics and Arctic Engineering. Halkidiki: OMAE, 2005:767-773.
[3] WILDE J D. Model tests on the vortex induced motions of the air can of a free standing riser system in current[C]∥ Proceedings of the Deep Offshore Technology Conference. Stavanger, Norway,2007.
[4] 王颖,杨建民,李欣.均匀来流中浮式圆柱的涡激运动研究[J].中国海洋平台, 2010, 25(1):8-15. WANG Ying,YANG Jianmin,LI Xin. Research on vortex-induced motions of a floating cylinder in uniform currents[J]. China Offshore Platform, 2010,25(1):8-15.
[5] 张蕙,杨建民,肖龙飞,等. 均匀流中深水系泊Truss Spar 平台涡激运动试验研究 [J].海洋工程, 2011,29(4):14-20. ZHANG Hui, YANG Jianmin, XIAO Longfei, et al. Experimental study of vortex-induced motions of a Truss Spar in uniform currents[J].The Ocean Engineering, 2011,29(4):14-20.
[6] 白治宁. 深吃水半潜式平台涡激运动响应特性研究[D].上海:上海交通大学.
[7] 唐友刚,樊娟娟,张杰. 高雷诺数下圆柱顺流向和横向涡激振动分析[J].振动与冲击,2013,32(13):88-92. TANG Yougang, FAN Juanjuan, ZHANG Jie. Analysis of in line and transverse vortex-induced vibration for a circular cylinder at high Reynolds number[J].Journal of Vibration and Shock, 2013,32(13):88-92.
[8] 康庄,贾鲁生.圆柱体双自由度涡激振动轨迹的模型试验[J].力学学报,2012,44(6):970-980. KANG Zhuang, JIA Lusheng. An experiment investigation on VIV trajectories of a two degree free vibration cylinder[J]. Journal of Theoretical and Applied Mechanics,2012,44(6):970-980.
[9] KHALAK A,WILLIAMSON C H K. Motion,force and mode transitions in vortex-induced vibration at low mass-damping[J]. Journal of Fluids and Structures, 1999, 13(7/8): 813-851.
[10] SARPKAYA T. A critical review of the intrinsic nature of vortex-induced vibrations[J]. Journal of Fluids and Structures, 2004, 19(4):389-447.
[11] STAPPENBELT B, LALJI F. Low mass ratio vortex-induced motion[C]∥ 16th Australasian Fluid Mechanics Conference. Gold Coast, Australia, 2007.
[12] ETIENNE S. FONTAINE E. Effect of the rotational degree of freedom on vortex-induced vibrations of a circular cylinder in cross-flow[C]∥ Proceedings of the 20th International Offshore and Polar Engineering Conference. Beijing, China, 2010.
[13] MINGUEZ M, LUPPI A,BERGER A. Slender buoy FSHR vortex induced rotations[C]∥ Proceedings of the ASME 31th International Conference on Ocean, Offshore and Arctic Engineering. Rio de Janeiro, Brazil: OMAE, 2012.
Model test investigation on vortex-induced motions of a buoyancy can
KANG Zhuang,LI Ping
(College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)
The vortex-induced motion(VIM) responses of a free vibration buoyancy can were studied experimently. The buoyancy can was put vertically, with a diameter of 150 mm and a length of 700 mm. By the model test, 6-DOF motion parameters were measured under different working conditions and the motion responses were analysed in the cross-flow, in-line and yaw directions. The results indicate that the in-line motion frequency is twice as high as that of the cross-flow motion and the trajectory of the cylinder is obviously in “8”shape when the reduced velocity becomes large. The yaw motion is of single frequency under a small reduced velocity and when the reduced velocity got larger, two frequencies appear and both increase as the reduced velocity increases,where the higher yaw motion frequency is equal to the cross-flow (CF) frequency. So, the CF motion and yaw motion come from a same excitation source, namely there is coupling effect. It is also found that the mean drag coefficient of VIM is about 100% more than that of the diffraction flow round the circular cylinder.
buoyancy can; vortex-induced motion (VIM); model test; “8”shape
国家自然科学基金(51009033)
2016-04-07 修改稿收到日期: 2016-05-31
康庄 男,博士,副教授,1978年生
李平 男,硕士生,1989年生
P756
A
10.13465/j.cnki.jvs.2017.14.002
