基于正则化核最大边界投影维数约简的滚动轴承故障诊断

赵孝礼, 赵荣珍, 孙业北, 何敬举

(兰州理工大学 机电工程学院， 兰州 730050)

基于正则化核最大边界投影维数约简的滚动轴承故障诊断

赵孝礼, 赵荣珍, 孙业北, 何敬举

(兰州理工大学 机电工程学院， 兰州 730050)

针对旋转机械故障诊断中故障样本获取困难的现状，提出一种基于正则化核最大边界投影(Regularized Kernel Maximum Margin Projection, RKMMP)维数约简的滚动轴承故障诊断方法。该方法首先利用RKMMP对小样本、少标记信息的混合故障样本集进行训练降维，然后将降维后的低维敏感特征子集输入到核极限学习机( Kernel Extreme Learning Machine, KLEM)分类器中进行故障识别。上述方法的特点是所提出的RKMMP能充分利用少量标记样本信息与大量无标记样本的故障信息，避免过学习的缺陷，同时通过添加正则化项克服小样本问题。滚动轴承故障模拟实验表明：该方法结合了RKMMP在维数约简和KLEM在模式识别上的优势，在一定程度上能提升故障诊断的泛化能力与识别精度。该研究可为解决好故障诊断中样本获取困难的问题，提供理论参考依据。

故障诊断；正则化核最大边界投影；核极限学习机分类器；维数约简

滚动轴承作为旋转机械中应用广泛且容易损坏的零部件，其运行状态正常与否直接影响到系统的工作性能，因此对滚动轴承进行故障诊断有着重大的现实意义[1]。振动信号分析是轴承故障诊断主要手段之一，从非线性、非平稳振动信号中提取出能综合反映故障状态的多域量化特征指标的方法，已被广泛应用于轴承故障诊断中[2]。但多域特征的引入使得多元冗余信息渗入其中，这将导致特征信息之间的相关性增大、数据的分类能力被严重恶化的问题。因此，需用维数约简方法对特征数据进行有效的二次特征提取，提取出低维敏感的主要特征矢量[3]。

故障特征数据的获取是基于维数约简的故障诊断方法的关键一环，故障数据常常具有“小样本、高维数”的特点[4]。在实际问题中，无标记的监测数据容易获取，而有标记的监测数据获取困难。若只利用少量有标记样本则会导致学习系统泛化能力差；若只利用无标记样本，则会浪费标记样本中有用信息。基于有监督与无监督降维算法的不足，综合利用少量标记信息和大量无标记信息，“半监督降维算法”逐渐成为解决此类问题的关键[5]。

最大边界投影(MMP)是He等[6]提出的半监督降维算法。该算法的特点是：通过有区别的构建不同类别标签的权重，最小化类内紧凑图的同时最大化类间分离图；使得高维数据的低维流形嵌入后，同类数据点更加紧密，异类数据点更稀疏。但MMP本质上是线性化的降维方法，处理非线性数据比较困难；此外，面对“小样本问题”仅通过PCA预处理效果不明显，且无监督模式容易丢失大量有用信息[7]。针对这两点不足，欲通过引入核方法，可将MMP的作用范围引入到非线性领域；进一步地，通过向目标函数添加正则化项克服小样本问题[8]，提出正则化核最大边界投影(RKMMP)算法，并将其应用到“小样本、少标记信息”故障数据维数约简的问题中。

故障诊断另一个核心问题是分类器的构建。核极限学习机(KELM)是Huang等[9]根据极限学习机(ELM)[10]的随机映射缺陷，提出的一种改进的新型网络学习方法。与传统分类器相比，KLEM具有学习速度快、泛化能力强、鲁棒性好等优点，在故障诊断等方面得到了广泛应用[11]。

鉴于上述分析，本研究拟对RKMMP与KLEM相结合的维数约简滚动轴承故障诊断方法进行探讨。欲为“小样本、少标记信息”的滚动轴承故障数据集的维数约简与类别划分，提供一种理论参考依据。

1 正则化核最大边界投影(RKMMP)算法简介

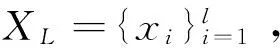
1.1 RKMMP算法的原理

MMP是LSDA[12]算法的半监督扩展，半监督学习的理论依据是根据先验一致性假设：即同类标签的样本具有相同的流形结构，异类标签的样本具有不同的流形结构[13]。MMP既可以利用大量无标记样本，避免过拟合问题；又可利用少量标记样本刻画数据的流形结构。为解决MMP算法无法有效处理小样本问题与非线性数据的缺陷，提出全新的RKMMP算法。

所提出的RKMMP算法基本思路为：首先，通过核函数将数据点映射到高维特征空间F中；然后，充分利用有标签与无标签信息，构造有区别的权重矩阵来描述类内与类间近邻图Gw、Gb，即最大化同类标签的数据点间的权重，最小化不同类别标签的数据点间的权重；通过向目标函数中添加正则化项并优化，使得映射后的同类样本间的点距离更近、异类更远。具体描述如下：

将样本点xi的近邻集合N(xi)分为:近邻样本集中与xi同类别的数据子集Nw(xi)和近邻样本集中与xi不同类别的数据子集Nb(xi)。定义Nw(xi)、Nb(xi)分别为：

(1)

Nb(xi)=N(xi)-Nw(xi)

(2)

式中:c(xi)表示xi的类别标签，k表示xi的近邻个数。

(3)

(4)

式中，γ为衡量权值数，参考文献[6]取值50。为使高维特征空间投影到低维特征空间后，类内近邻图数据点更加紧凑，同时类间图数据点更加离散，建立两个优化目标函数,即：

(5)

(6)

式中:Dw、Db分别为类内、类间对角矩阵，Lb=Db-Wb。对式(5)施加一个约束条件aTXDwXTa=1，进一步地将式(5)简化为：

(7)

综合两目标函数式(6)、(7)，得到MMP的优化目标函数，即：

(8)

将式(8)转换成求解广义特征值问题见式(9)，即

X(βLb+(1-β)Ww)XTa=λXDwXTa

(9)

当训练样本数目小于样本的特征维数时,MMP算法会出现病态奇异矩阵问题，也就是“小样本问题”。这容易导致MMP无法计算出最佳投影矩阵或计算结果不稳定。为使奇异矩阵变成正定矩阵，通过添加一个正则化常数δ与单位矩阵I乘积所得常数矩阵δI作为正则因子，即将式(9)转变为RMMP的广义特征值问题：

X(βLb+(1-β)Ww)XTa=λ(XDwXT+δI)a

(10)

RKMMP则是通过引入式(11)所示的RBF核函数，将RMMP的应用扩展到非线性领域。

Ki,j=<φ(xi),φ(xj)>=exp(-‖xi-xj‖/t)

(11)

式中:φ表示非线性函数;t表示核参数。在Hilbert空间F中式(10)变形为

φ(X)[βLb+(1-βWw](X)Taφ=
λ[φ(X)Dwφ(X)T+δI]aφ

(12)

式中，aφ是由F空间所有向量线性组合而成的解向量，则存在向量aφ=[a1,a2,..,an]满足：

(13)

结合式(12)、(13)，对式(12)两边做内积，可得KRMMP优化目标式(14)：

K[βLb+(1-β)Ww]Ka=λ(KDwK+δI)a

(14)

1.2 RKMMP算法的实现流程

RKMMP算法具体步骤如下：

输入：高维空间数据集X={(x1,c1), (x2,c2),..(xl,cl),xl+1,...xl+u},xi∈Rd,

输出：低维特征向量Y，投影映射矩阵A。

(1)将原始数据集X进行数据归一化，得到Xo。

(2)将Xo通过核函数K(·)映射到高维特征空间F中，得到φ(Xo)。

(3)利用有标记样本和未标记样本，根据式(5)、(6)通过k近邻法对数据集构造类内、类间近邻图。

(4)根据权值矩阵，求解式(14)的广义特征值和特征向量。得前m个最小非零特征值对应的特征向量，构成投影向量aφ={a1，a2,…，am}，并将φ(Xo)通过a进行降维投影，得到映射后的低维特征集Y=aTφ(Xo)。

2 核极限学习机(KELM)算法简介

2.1 KELM分类器

KELM作为ELM算法的扩展，是由Huang等根据SVM与ELM的优化角度，将核函数引入到极限学习机中，克服了随机初始值导致的不稳定问题。

(15)

式中：β表示输出权重矩阵；h(xp)表示输入xp经隐含层映射后的输出矩阵；若ELM的隐含层输出函数G(w,x,b)已知，则计算h(xp)形式如下

h(xp)=[G(w1·xp+b1),…,G(wL·xp+bL)]

(16)

式中:w为输入权值，b为偏值；w、b在训练中随机赋值。

由Karush-Kuhn-Tucker (KKT)定理可知，ELM的训练学习等效为求解如式(17)的对偶优化问题：

(17)

式中：C为惩罚系数，用以权衡结构风险和经验风险之间的比例；τp表示理论输出tp与实际输出f(xp)的误差；αp为拉格朗日算子，求解式(17)可得：

(18)

式中：H为隐含层输出矩阵，T=[t1,t2,...,tN]表示输入样本集的目标向量。HHT在求解广义逆过程中，因数据存在复共线性导致HHT非奇异，容易引起不稳定现象。故将核函数思想引入ELM中，根据Mercer条件定义核矩阵：

Ψ=HHT∶Ψi,j=h(xi)·(xj)=K(xi,xj)

(19)

通过核矩阵K代替HHT，由式(18)、(19)代入式(15)中得KLEM输出模型：

f(xp)=[K(xp,x1),…,K(xp,x1)]ζ

(20)

(21)

式中，ζ即为KELM网络的输出权值。

由以上过程可知，通过向KELM添加偏值常量1/C，可增加系统的稳定性与泛化能力；同时KLEM无需设置众多参数，只需选择合适的核函数。相对于ELM，KELM解决分类与回归问题效果更好，具有更强大的非线性逼近能力。

2.2 KELM分类器故障辨识流程

KLEM算法故障辨识流程图见图1。它的具体实现步骤如下：

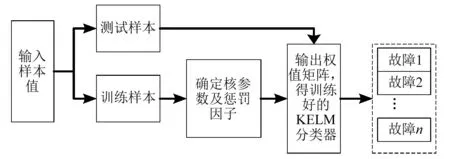
图1 KELM分类器的故障辨识流程图Fig.1 The flow chart of fault identification of the KELM classifier

(1)将输入样本分为训练样本集与测试样本集，确定核参数及惩罚因子。

(2)求解出输出权值β，寄存KELM参数，得训练学习后的KELM分类器。

(3)将测试样本与训练样本输入KLEM分类器中进行故障诊断。

3 设计的RKMMP维数约简的故障诊断方法

3.1 混合故障数据集、RKMMP与KELM相结合的故障诊断方法的探讨

为解决故障诊断过程中，训练样本与有标记信息样本较少导致故障诊断困难的现状。拟以轴承故障数据集为实验对象，提出RKMMP维数约简与KELM分类器相结合的故障诊断方法。该方法所提出的RKMMP半监督降维方法，一方面能综合利用少量有标记故障样本与大量无标记故障样本，提取出最佳分类的低维特征子集，另一方面正则化与核方法的引入能有效克服小样本问题，增强其处理非线性问题的能力。故障诊断的实质是模式识别，方法中的KELM分类器能快速、稳定、精确地实现故障类别的量化表征。

所设计的故障诊断方法主要思路为：首先，以滚动轴承的振动信号为对象，从时域、频域、时频域等多方面构建能全面反映故障信息的高维、小样本、少标记信息的混合故障数据集，然后将数据集输入到RKMMP中降维处理，得到低维敏感的特征子集；最后，将低维特征子集输入到KELM分类器中进行训练学习与故障辨识，得出故障诊断结果。

3.2 故障诊断方法实现的流程与步骤

设计的基于RKMMP维数约简的故障诊断方法流程，见图2。整个故障诊断方法由如下几个步骤实现：

图2 故障诊断方法流程图Fig.2 The flow chart of fault diagnosis method

步骤1 对机械振动信号进行采集，从时域、频域和时频域方面做特征提取，得到原始数据特征集X。

步骤2 根据故障数据的具体特性确定核参数t，并将特征集经高斯核函数K(·)映射到高维特征空间F，在此空间进行RMMP降维，得到低维特征集Y。

步骤3 将低维特征集Y输入KELM进行模式识别，得到测试样本的故障类型。

4 实验结果与分析

4.1 实验数据的来源

实验中所采用的实验数据来源于美国凯斯西储大学(CWRU)电气工程实验室的滚动轴承实验数据[14]。实验轴承的型号为6205-RS JEM SKF深沟球轴承。轴承的具体参数为：内径25 mm，外径52 mm，厚度15 mm，滚动体直径8.18 mm。实验所选取的数据是在如下条件下测得：电机负载为2 hp，在采样频率为48 kHZ，转速为1 750 r/min情况下，通过驱动端轴承座上的加速度传感器拾取振动信号。实验中轴承的损伤是用电火花加工模拟，选取故障尺寸为直径0.53 mm、深度为0.28 mm(故障等级为严重)的三种典型故障类型：外圈故障、内圈故障、滚动体故障。以2 048个采样点为一组样本，分别截取轴承外圈、轴承内圈、滚动体故障以及正常四种状态下的振动信号各50组，以其中每种状态的20组作为训练样本(其中前5组为有标记故障样本，后15组为无标记样本)，余下的30组作为测试样本。为建立高维、小样本混合故障特征集，需从时域、频域、时频域多个角度构建如表1的特征集合，共得到108个特征参数(得到4×20×108维的小样本故障数据特征集)。其中，因轴承信号包含四种故障类型，故EMD最少能分解出4个固有模态函数(IMF)和一个余项信号，为充分把握原数据的特征信息，提取前5层IMF分量及复杂度作为能量特征，即35～44号特征；同时采用db4小波包函数对振动信号进行6层正交小波包分解，分解出的各频带的能量特征，即45～108号特征。

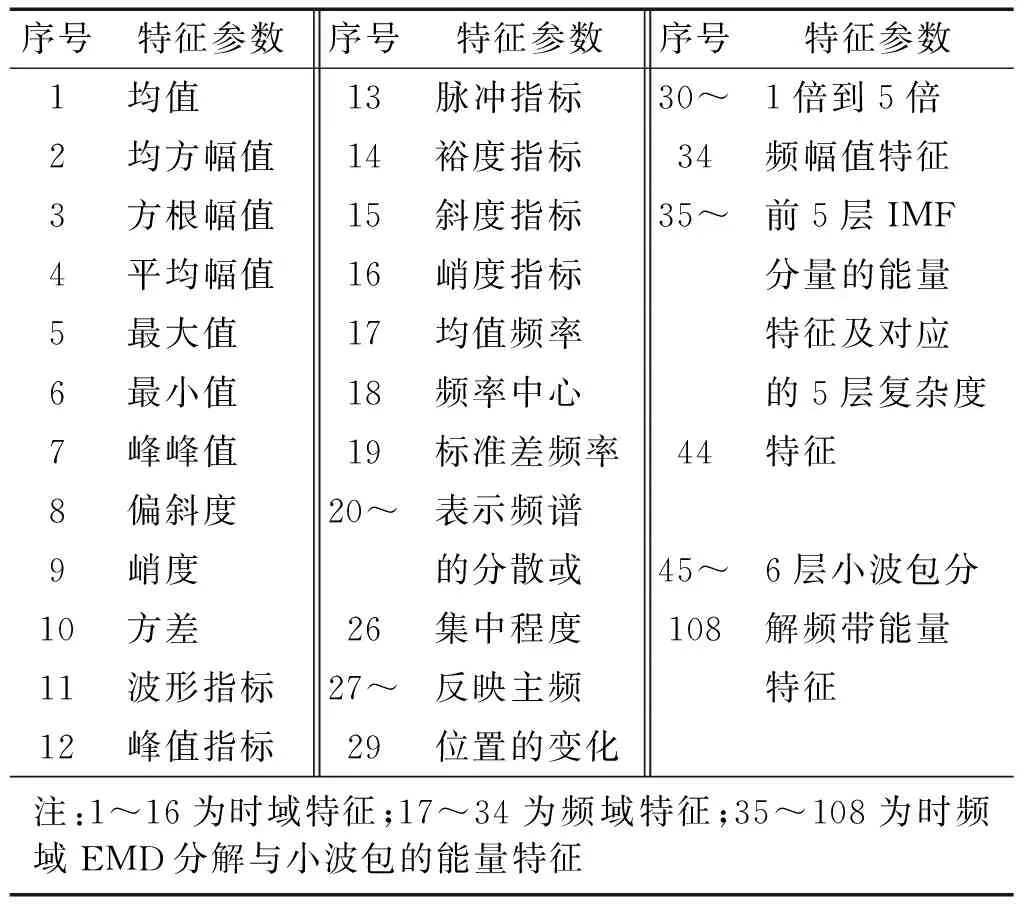
表1 特征参数

4.2 应用情况与分析

从实验数据中构建高维混合故障特征集，输入到RKMMP中进行维数约简，再通过KELM分类器进行故障识别。根据文献[6]，设置参数近邻值k=5、调节因子设置为0.5、正则化因子设置为1；为充分涵盖原始数据集的本质信息，目标维数统一降维到3维(目标维数=故障类别数-1)；为验证所提方法的有效性，分别采用PCA、KPCA、KLSDA、MMP、KMMP算法对原始故障数据集进行维数约简(其中，KLSDA、MMP、KMMP经过PCA预处理)，作对比试验。为方便后续工作，分别记六种算法{PCA, KPCA, KLSDA, MMP, KMMP, RKMMP}={R1, R2, R3, R4, R5, R6}。对核函数参数选取，采用五折交叉法选取最优高斯核参数，得到KPCA、KLSDA、KMMP、RKMMP的核参数分别为t=88、75、20、60。在降维过程中，半监督算法只利用有标记故障样本，无监督算法利用所有样本，但不利用故障标签信息；有监督算法只利用有标记样本进行降维学习。为评估方法的有效性，实验从以下三个角度进行验证：

4.2.1可视化降维与故障辨识结果对比

将故障数据集输入到降维算法中，得六种方法的降维后测试样本三维嵌入图，见图3。

(a)PCA (b)KPCA (c)KLSDA

(d)MMP (e)KMMP (f)RKMMP图3 测试样本基于不同方法的降维结果Fig.3 The test sample results based on different methods of dimensionality reduction

从图3可以看出：RKMMP降维后的聚类与分类效果最好，其降维后的各故障类内距离小、类间间距明显；PCA的降维后测试样本聚类与分类效果最差；其他四种算法聚类与分类效果介于二者之间。除RKMMP外，其他五种降维方法的故障间都存在着一定程度的交叉混叠现象，其中外圈与滚子故障降维效果六种算法都不理想；正常状态的各类算法降维结果都较为成功。

同时，将降维后的低维特征子集输入ELKM分类器中进行故障模式识别。KLEM核函数取RBF型，交叉优化参数得C=100，t=40。训练得到六种算法降维后各类故障的识别准确率，见图4所示(其中，外圈、轴内圈、滚动体以及正常四类状态分别记为F1、F2、F3、F4，而F5为四类故障的总体平均识别率)。图4中，六种降维方法的总体平均识别率逐渐上升，平均识别率RKMMP最高，PCA最低；针对单个故障，滚子故障的识别率六类算法都未能准确划分出；正常状态识别率最好，六种算法都能准确识别出来。

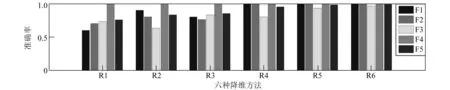
图4 六类算法的故障诊断结果Fig.4 Fault diagnosis result of six algorithms

由图3、图4得如下结论：

1) PCA的降维效果及识别正确率最差，这由于PCA是基于二阶统计信息，只能保持数据的最大方差方向投影，忽略了原始特征空间的非线性特征结构，故效果较差；KPCA降维效果及识别率一般，这是因为KPCA虽然具有较强的非线性提取能力，但其保持局部信息的能力较低；PCA、KPCA无监督方式导致其无法在类别信息的指导下进行维约简，易丢失大量利于分类的信息，整体识别率较低。

2) KLSDA、MMP的降维效果及识别正确率一般。这是由于KLSDA虽然能挖掘出局部流形结构信息，但过度依赖于少量有标记的故障样本，导致过学习问题，无法取得理想的故障诊断结果；MMP虽然能够综合利用有类别标签与无类别标签信息，但MMP本质是线性降维方法，故降维与辨识结果未能取得最优。

3) RKMMP降维与故障识别结果比KMMP等其它五种方法都好的原因是，KMMP无法克服小样本问题，PCA处理后容易丢失大量有用信息，导致无法取得最优。RKMMP既能利用无标记故障样本中的故障信息，又能克服KLSDA等有监督算法出现的过学习问题，核方法及正则化的改进提高了其应用范围及泛化能力，故取得最优的故障诊断结果，图3的降维情况与图4的结果证明了基于RKMMP维数约简的故障诊断方法的有效性。

4.2.2 RKMMP解决小样本与少标记信息的性能验证

为测试RKMMP算法对小样本问题处理能力，通过改变各类故障的训练样本与测试样本的比例，设置每组10/40、15/35、20/30、25/25、30/20、40/10(其中训练样本小于25时为小样本情况，有标记故障样本为前5个不变)。并得六类降维算法低维测试样本输入KELM分类器所得的平均识别率，见图5。

图5 不同训练样本数对应的平均识别准确率Fig.5 The average recognition accuracy of different training sample

从图5中可以看出：①总体上，除KLSDA只利用有标记故障样进行训练不变外，其他五种降维方法的识别准确率都随着训练样本数的增加而增加，这是因为训练样本越多，就越能表征数据的整体情况，故障识别率得到一定提升;②PCA、KPCA在少训练样本情况下，准确率下降明显；MMP、KMMP虽然在一定程度能够克服小样本问题，但效果不明显，这是因为PCA预处理作为无监督方式，容易丢失大量分类信息，不能有效处理“小样本问题”，导致故障诊断效果下降;③其中，RKMMP的稳定性能最好，即使在小样本情况下也能取得较高的识别率，这是因为正则化的改进对小样本问题处理效果明显，从而说明RKMMP能够有效处理小样本问题，推广适应能力较强。

为进一步地验证方法中RKMMP综合利用有标记与无标记样本的能力，即测试算法中标记样本与无标记样本比例对降维效果的影响。设置如下实验选取训练样本与测试样本比例为30/20不变(去除小样本因素影响)，分别依次增加各类故障有标记样本数目，设置各状态有标记训练样本分别为2、5、10、15、20、25、30个。经RKMMP等算法训练降维后，并得低维测试样本输入KELM分类器所得的平均识别率，见图6。

从图6中可以看出：

(1)随着训练类别标签样本数的增加，KLSDA、MMP、KMMP、KRMMP的分类识别率随之增加，这是因为随着故障标记的增加，先验信息越多，过拟合现象随之减少，故障识别率增加。而PCA、KPCA无监督算法无法利用有标记故障样本，故无影响。

(2)其中，有监督学习算法KLSDA受故障标记影响较大，识别率变化比较明显，说明有监督算法严重依赖故障标记信息；而半监督算法对少量类别标记的训练样本也有着良好的故障分类性能，说明半监督算法能够同时利用样本的有标记与无标记故障信息。

(3)RKMMP的稳定性能最好，识别准确率一直高于其他算法；尤其是在标记样本极其少量的情况下，RKMMP、KMMP、MMP等半监督算法就能获得较高的故障诊断精度，进而说明半监督学习算法的在处理少量有标记故障样本时的优越性。

图6 有故障标记数目对故障诊断的影响Fig.6 The influence of fault labeled number for fault diagnosis

4.2.3 方法中KELM分类器的性能验证

为进一步验证分类器KELM优异的鲁棒性与稳定性，训练与测试样本之比为20/30等参数不变的情况下。参考文献[15]向原始混合故障数据集中添加系数a=0.1、0.2、0.4、0.8的随机干扰噪声，将经RKMMP降维后的结果输入到KELM、BP、SVM、ELM分类器进行的故障辨识结果作对比，得到故障识别平均准确率，如表2所示。

由表2中可以看出：添加随机噪声后，ELM的故障诊断结果波动较大，而KELM变化小；说明KELM的识别率的稳定性要优于ELM，原因是ELM初始值的随机性导致其训练不稳定且泛化能力差，KELM在核映射条件下稳定性能更好；由此证明了经RKMMP降维后的KELM分类器具有较好的鲁棒性能，稳定性好、泛化能力强的特点。

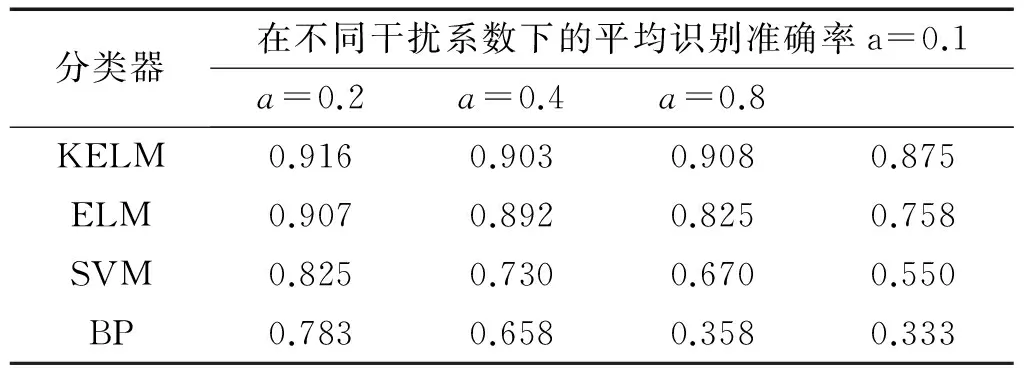
表2 不同分类器的抗干扰能力对比

5 结 论

为解决故障诊断过程中故障样本获取困难的现状，提出基于改进的半监督降维算法RKMMP维数约简的滚动轴承故障诊断方法。首先，新提出的RKMMP算法具有良好的维数约简能力，能充分利用有标签与无标签信息，克服小样本问题，提取出低维敏感、具有鉴别能力的特征子集；然后，将低维特征子集输入到KELM分类器中，KELM分类器能更精确、稳定地实现故障类别的划分，适应多类样本问题。实验结果表明，所提方法能够对少训练样本、少标记信息的轴承故障数据集进行有效地维数约简与故障辨识，为滚动轴承故障诊断提供了一种新的解决思路。该研究后续工作可以从以下几个方面进行：

(1)只对轴承的严重故障进行诊断，尚未涉及对早期、轻度等故障类型进行诊断。

(2)KELM分类器的核参数选取只采用交叉验证获得，需要进一步的优化。

[1] 张文义，于德介，陈向民. 基于信号共振稀疏分解与能量算子解调的轴承故障诊断方法[J]. 中国电机工程学报，2013, 33(20):111-118.

ZHANG Wenyi, YU Dejie, CHEN Xiangmin. Fault diagnosis of rolling bearings based on resonance-based sparse signal decomposition and energy operator demodulating[J]. Proceedings of the CSEE, 2013, 33( 20): 111-118.

[2] 黄宏臣，韩振南，张倩倩，等. 基于拉普拉斯特征映射的滚动轴承故障识别[J]. 振动与冲击，2015,34(5): 128-134.

HUANG Hongchen, HAN Zhennan, ZHANG Qianqian，et al. Method of fault diagnosis for rolling bearings based on Laplacian eigenmap[J]. Journal of Vibration and Shock, 2015,34(5): 128-134.

[3] 李锋，汤宝平，陈法法. 基于线性局部切空间排列维数化简的故障诊断[J]. 振动与冲击，2012, 31(13): 36-40.

LI Feng, TANG Baoping, CHEN Fafa. Fault diagnosis model based on dimension reduction using linear local tangent space alignment[J]. Journal of Vibration and Shock, 2012, 31(13): 36-40.

[4] 韦佳，杨创新，马千里，等. 基于局部重构与全局保持的半监督判别分析方法[J]. 华南理工大学学报(自然科学版)，2010, 38(7):45-49.

WEI Jia, YANG Chuangxin, MA Qianli, et al. Semi-supervised discriminant analysis method based on local reconstruction and global preserving[J]. Journal of South China University of Technology(Nature Science Edition), 2010, 38(7):44-49.

[5] ZHU X. Semi-supervised learning literature survey[J]. Computer Science, 2008, 37(1):63-77.

[6] HE X, CAI D, HAN J. Learning a maximum margin subspace for image retrieval[J]. IEEE Transactions on Knowledge & Data Engineering, 2008, 20(2):189-201.

[7] JIANG L, SHI T, XUAN J. An intelligent fault diagnosis method of rolling bearings based on regularized kernel Marginal Fisher analysis[C]// Journal of Physics: Conference Series, 2012:597-604.

[8] PIMA I, ALADJEM M. Regularized discriminant analysis for face recognition[J]. Pattern Recognition, 2004, 37(9):1945-1948.

[9] HUANG G B, ZHOU H, DING X, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems Man & Cybernetics, Part B: Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society, 2012, 42(42):513-529.

[10] HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1/2/3):489-501.

[11] 陈绍炜，柳光峰，冶帅. 基于核极限学习机的模拟电路故障诊断研究[J]. 西北工业大学学报，2015, 33(2):290-294.

CHEN Shaowei, LIU Guangfeng, YE Shuai. A method of fault diagnosis for analog circuit based on KELM[J]. Journal of Northwestern Polytechnical University, 2015,33(2):290-294.

[12] CAI D, HE X, ZHOU K, et al. Locality sensitive discriminant analysis[C]. IJCAI, 2007:708-713.

[13] 杨望灿，张培林，吴定海，等. 基于改进半监督局部保持投影算法的故障诊断[J]. 中南大学学报(自然科学版)，2015, 47(6):2059-2064.

YANG Wangcan, ZHANG Peilin, WU Dinghai, et al. Fault diagnosis based on improved semi-supervised locality preserving projections[J]. Journal of Central South University(Science and Technology), 2015, 47(6): 2059-2064.

[14] LOPARO K A. Bearings vibration data set, Case Western Reserve University [DB/OL]. http://csegroups.case.edu/bearingdata-center/home.

[15] CHEN F, TANG B, CHEN R. A novel fault diagnosis model for gearbox based on wavelet support vector machine with immune genetic algorithm[J]. Measurement, 2013, 46(1):220-232.

Fault diagnosis of rolling bearings based on the dimension reduction using the regularized kernel maximum margin projection

ZHAO Xiaoli, ZHAO Rongzhen, SUN Yebei, HE Jingju

(School of Mechanical and Electronical Engineering, Lanzhou University of Technology, Lanzhou 730050, China)

In view of the difficulty of fault samples’ acquisition in the fault diagnosis of rotating machinery, a novel fault diagnosis method for rolling bearings based on the dimension reduction using the regularized kernel maximum margin projection (RKMMP) was proposed. In the method, the RKMMP was used to reduce the dimension of the mixed fault data set of small samples and less labeled information. Then the low-dimensional sensitive feature subset was input into a kernel extreme learning machine (KLEM) classifier for training and fault identification. The characteristics of the method is that the proposed RKMMP can make full use of the labeled information of small samples and the fault information of numerous unlabeled samples, and avoid the problem of over-fitting. At the same time, a regularization term was added to overcome the disadvantage of small samples. The simulations on rolling bearing fault diagnosis show that the method combines the advantages of RKMMP in dimension reduction and of KLEM in pattern recognition. To a certain extent, it can improve the generalization ability of fault diagnosis and the accuracy of recognition. The study solves the problem of samples’ acquisition and provides a theoretical support to the rolling bearing fault diagnosis.

dynamic response ; multiaxial random excitation; vibration fatigue; modal shape

国家自然科学基金(51675253)；高等学校博士学科点专项科研基金(20136201110004)

2016-04-20 修改稿收到日期： 2016-06-12

赵孝礼 男，硕士生，1991年生

赵荣珍 女，博士，教授，博士生导师，1960年生

TP18; TH165

A

10.13465/j.cnki.jvs.2017.14.016