新型Ti-Al金属间化合物多孔材料有效泊松比的理论表征

苏淑兰，饶秋华，贺跃辉

新型Ti-Al金属间化合物多孔材料有效泊松比的理论表征

苏淑兰1，饶秋华2，贺跃辉3

(1. 中南林业科技大学 土木工程与力学学院，长沙 410004；2. 中南大学 土木工程学院，长沙 410075；3. 中南大学 粉末冶金研究院，长沙 410083)

基于新型Ti-Al金属间化合物多孔材料真实孔隙的空间结构特征，采用三维八面体结构模型，首次通过能量法推导出表征多孔材料有效泊松比的理论公式，给出有效泊松比与其相对密度的显式表达式。并以圆形截面的孔棱为例，将本文有效泊松比与已有结果进行比较。结果表明：本文方法表征有效泊松比理论公式的推导过程更简单直接，所得结果更合理可靠。同时分析了孔棱横截面的几何形状和孔棱变形时剪力对有效泊松比的影响规律。分析表明，两者对有效泊松比的影响均随相对密度增大而增加，当相对密度较大时必须考虑剪力的影响。

Ti-Al金属间化合物；多孔材料；八面体模型；能量法；泊松比

多孔材料具有比表面积大、比力学性能高和吸附容量大等特殊性能，可实现过滤、分离、吸附及减震等多种功能，已广泛应用于化工、环境保护、航空航天和结构工程等工程领域[1−5]。本课题组研发的Ti-Al金属间化合物多孔材料是一类新型的金属间化合物多孔材料[6]，它兼备陶瓷和金属多孔材料的性能优势[7−11]，具有更高的比强度和比模量、更好的耐高温和氧化性能，作为一种优异的轻质高强结构和功能材料，其基本力学性能(如弹性模量、剪切弹性模量和泊松比)的表征是实现工程应用的前提。多孔材料因孔隙微观结构的复杂性和非均匀性，力学性能表征已成为材料制备与应用研究中的难点和热点问题之一。多孔材料力学性能的理论表征大都是通过建立二维或三维的多孔结构模型[12]。二维结构模型[13−15]不能真实反映多孔材料的孔隙结构特点；三维结构模型因其空间结构的复杂性使其实际应用受到很大的限制。KIM等[16]由构建的六棱柱模型得到正交各向异性的有效弹性常数；LI等[17]选取1个十四面体和ZHU等[18]选取一个BCC晶格中的3个十四面体，两者都得到了加载平面内具有各向异性的有效弹性常数；刘培生[19]建立了八面体模型，利用棱柱变形的几何关系来推演有效弹性常数的数理关系。以上都是通过建立孔隙结构模型推导出多孔材料性能的理论表征，显然模型的复杂性与推导过程的繁琐性成正比，故人们希望建立尽量简化的理论模型来简捷而方便地表征出实际状态的有效特征和性能行为。本文在前期对多孔材料力学性能研究工作[20−21]的基础上，进一步探讨三维多孔结构弹性性能的理论表征。基于新型Ti-Al金属间化合物多孔材料真实孔隙的三维结构特征，采用三维八面体结构模型，在已有弹性模量理论公式的基础上，通过能量法推导出多孔材料有效泊松比的理论计算公式，以期为多孔材料的工程实际应用提供理论指导。

1 八面体结构模型建立

考虑到多孔材料真实孔隙的空间结构特征，将其抽象为三维几何多面体，建立多孔材料的三维孔隙结构模型，如图1所示的立方结构模型[12]、六棱柱模型[16]、十四面体模型[17−18]和八面体模型[19]。其中立方结构模型具有结构均匀和各向同性的特点，为三维孔隙结构的经典。考虑到多孔材料真实孔隙的空间结构特征，将其抽象为几何多面体，建立多孔材料的三维孔隙模型。但立方结构模型的孔隙单元无法实现密堆积，且棱柱结构受力状态不等价；六棱柱模型和十四面体模型均能实现空间密堆积，但前者结构不均匀且不能实现各向同性，后者能实现各向同性但结构不均匀；在八面体模型中，构成孔隙单元的8根孔棱全部由立方体体心与立方体顶点的连线组成，故组成孔隙单元的所有孔棱全部等价，且所有孔棱均规则地按立方体的对角线方式连接，形成大量密堆积的体心立方式八面体孔隙单元，能同时满足孔隙单元密堆积、孔棱全部等价及三维各向同性。图2所示为本课题组制备的新型Ti-Al金属间化合物多孔材料的孔结构形貌，本文将其孔隙结构抽象为八面体结构模型，如图1(d)所示。

图1 三维孔隙结构模型Fig.1 3D pore structure model (a) Cubic structure; (b) Hexagonal prism; (c) Tetrakaidecahedral; (d) Octahedron

图2 Ti-Al金属间化合物多孔材料的孔结构形貌Fig.2 Pore structure morphology of the Ti-Al porous material

设孔棱材料为各向同性、线弹性，选取一个立方体为多孔单元体，且立方体边长为2a，孔棱横截面面积为A，则孔棱长度L，横截面惯性矩I以及多孔体的相对密度ρ(即ρ*/ρs)为：

式中：c为孔棱横截面的回转半径，ρ*和ρs分别为多孔材料和致密材料的密度。

2 理论公式推导

首先求得多孔体在远场均匀应力σ1作用下的横向线应变1ε′。设多孔体同时受X1方向远场均匀拉应力σ1和X2方向远场均匀压应力σ2的作用，如图3所示；多孔体受合力4P1(X1方向)和4P2(X2方向)作用，如图4所示。由于结构和载荷的对称性，8根孔棱受力均相同，只需分析其中的任意一根孔棱如O1A即可，如图5所示。

由前期工作[20]中的分析可知，在σ1和σ2共同作用下，孔棱O1A分别产生内力N1，Q1，M1以及N2，Q2和M2，即：

由图中几何关系可知，在σ1和σ2共同作用下孔棱O1A的内力合力为：

图3 单元八面体受远场应力σ1和σ2作用Fig.3 Unite octahedron subjected to uniform stress σ1and σ2

根据能量法，卡氏第二定理计算单元体结构位移的公式如下：

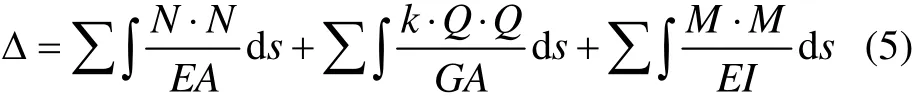
图4 单元八面体受合力作用Fig.4 Unite octahedron subjected to resultant force

图5 σ1和σ2共同作用下孔棱O1A的受力分析Fig.5 Force analysis of the strut O1A

令式(6)中P2=0，且考虑到结构的对称性，可得到受远场均匀应力σ1作用时单元体沿X2方向产生的线位移Δ12=2ΔL，即：

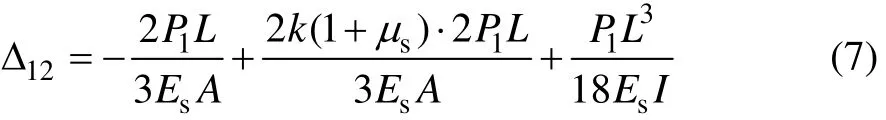
则多孔体在远场均匀应力σ1作用下的横向线应变1ε′为：

设多孔体受到远场均匀应力σ1作用时，单元体沿X1方向的纵向线应变ε1在前期工作[20]中已有，即：

将(8)和式(9)代入式(2)，同时考虑式(1)，可得单元体在X1−X2面内的有效泊松比为：

3 模型验证与分析

3.1 现有模型结果对比

文献[17]采用十四面体模型，由卡氏第二定理得到的理论公式为：

文献[18]采用十四面体模型，由Love最小势能原理得到的理论公式为：

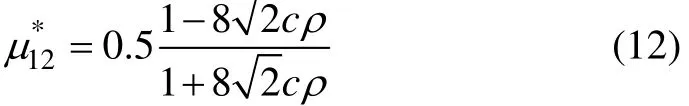
表1所列为八面体孔棱横截面形状分别为圆形、方形、三角形和plateau的几何参数(回转半径c和横向剪切系数k)，设致密材料的泊松比μs=0.33。

表1 孔棱横截面的几何常数Table 1 Geometric parameters of the cross section

以圆形截面的孔棱为例，图6所示为本文、文献[17]和文献[18]计算得到的有效泊松比/Es随相对密度ρ*/ρs的变化曲线。可知，/Es值随ρ*/ρs的增大而减小，但在整个相对密度范围内变化不大。这是由于孔隙的存在使得多孔材料在纵向荷载作用下更容易产生较大的横向变形，但同时其纵向变形也会相应增大，最终导致其泊松比稍大于致密材料。故孔隙对多孔材料的/Es有一定影响，但影响不大，该结论与文献[13]和文献[19]的研究结果一致。与均采用十四面体模型的文献[17]和文献[18]比较，两者因选取不同的孔隙单元而得到变化各异的有效泊松比，故本文八面体模型采用能量法推导过程更为简单直接，所得结果更为合理可靠。

图6 随ρ*/ρs的变化曲线Fig.6 Variation ofwith ρ*/ρs

图7所示为孔棱横截面形状分别为圆形、方形、三角形和plateau截面时计算得到的有效泊松比随相对密度ρ*/ρs的变化曲线。由计算结果可见，当相对密度较小时，孔棱横截面形状对的影响不大；随相对密度增大，孔棱横截面形状对的影响增大。对于同一相对密度的值，对称的圆形和方形截面几乎相同且为最大、三角形截面居中、plateau截面为最小，与文献[16]的研究结论相同。

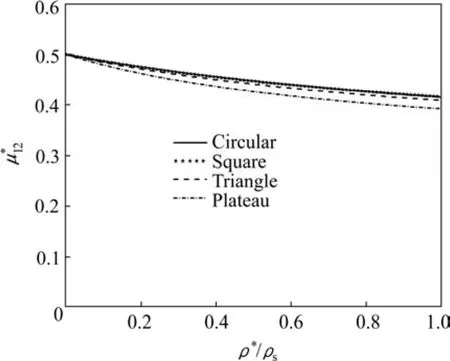
图7 孔棱横截面形状对的影响Fig.7 Effects of strut cross section shapes on

以圆形截面的孔棱为例，图8所示为考虑剪力和不考虑剪力时有效泊松比随相对密度ρ*/ρs的变化曲线。可见，当ρ*/ρs较小时，因孔棱可简化为欧拉梁，剪力对的影响很小可忽略不计，故考虑剪力和不考虑剪力时计算得到的值几乎重合；当ρ*/ρs较大时，孔棱则视为铁木辛柯梁，必须考虑剪力的影响，剪力对的影响随ρ*/ρs增大而增加，该结论与文献[17]一致。

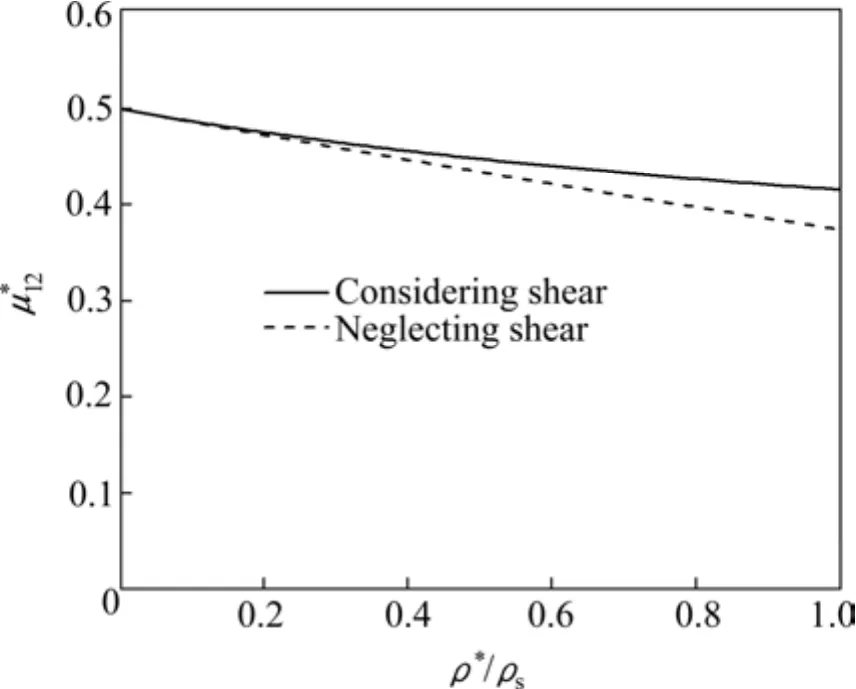
图8 剪力对的影响Fig.8 Effects of shear force on

4 结论

1) 基于新型Ti-Al金属间化合物多孔材料真实孔隙结构的空间结构特征，采用三维八面体结构模型，首次通过能量法推导出该多孔材料有效泊松比的理论计算公式，为该材料的工程实际应用提供了可靠的理论依据。

REFERENCES

[1] YAMAGUCHI A, UEJO F, YODA T, et al. Self-assembly of a silica-surfactant nanocomposite in a porous alumina membrane [J]. Nature Materials, 2004, 3(5): 337−341.

[2] HERNANDEZ N, SANCHEZ-HERENCIA A, MORENO R. Forming of nickel compacts by a colloidal filtration route[J]. Acta Materialia, 2005, 53(4): 919−925.

[3] VAN D B B, VANDECASTEELE C. Distillation vs. membrane filtration: Overview of process evolutions in seawater desalination[J]. Desalination, 2002, 143(3): 207−218.

[4] ARIRIATU L E, EWELIKE N C. A low-cost filtration system for the treatment of wastewaters[J]. Environment Protection Engineering, 2003, 29(2): 17−22.

[5] 刘培生. 多孔材料引论[M]. 北京: 清华大学出版社, 2004. LIU Peisheng. Introduction of Porous Materials[M]. Beijing: Tsinghua University Press, 2004.

[6] 江垚. Ti-Al金属间化合物多孔材料的研究[D]. 长沙: 中南大学, 2008: 43−46. JIANG Yao. Investigation on Ti-Al intermetallic compound porous material[D]. Changsha: Central South University, 2008: 43−46.

[7] 李婷婷, 彭超群, 王日初, 等. Fe-Al、Ti-Al和Ni-Al系金属间化合物多孔材料的研究进展[J]. 中国有色金属学报, 2011, 21(4): 784−795.

LI Tingting, PENG Chaoqun, WANG Richu, et al. Research progress in porous Fe-Al, Ti-A1 and Ni-A1 intermetallic compound porous materials[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(4): 784−795.

[8] 郝刚领, 许巧平, 李先雨, 等. 超轻TiAl多孔材料的阻尼响应特征[J].有色金属工程, 2016, 6(4): 2−5.

HAO Gangling, XU Qiaoping, LI Xiangyu, et al. Damping characteristics of ultra-light TiAl porous materials[J]. Nonferrous Metals Engineering, 2016, 6(4): 2−5.

[9] 杨帆, 田楠, 王帆, 等. 基于TiAl多孔载体的钙钛矿型催化剂的汽车尾气催化性[J]. 功能材料, 2013, 18(44): 2616−2619.

YANG Fan, TIAN Nan, WAND Fan, et al. Purification of motor vehicle exhaust gas by perovskite catalyst based on the porous TiAl alloys[J]. Journal of Functional Materials, 2013, 18(44): 2616−2619.

[10] WAN Ling, WANG Zhanyi, WEI Xing, et al. Mechanism of anti-arterial thrombosis of Dahuangzhecong Fang screened by Ti-Al intermetallic compound porous material[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(12): 3156−3160.

[11] 何薇, 梯度孔径TiAl金属间化合物多孔材料制备技术的研究[D]. 长沙: 中南大学, 2012: 35−36.

HE Wei. Fabrication of gradient porous Ti-A1 intermetallic compound[D]. Changsha: Central South University, 2012: 35−36.

[12] GIBSON L J, ASHBY M F. Cellular Solids: Structure and Properties[M]. Second edition Cambridge: Cambridge University Press, 1997.

[13] CHRISTENSEN R M. Mechanics of cellular and other low-density materials[J]. International Journal of Solids and Structures, 2000, 37(1/2): 93−104.

[14] RAMAKRISHNAN N, ARUNACHALAM V S. Effective elastic moduli of porous solids[J]. Journal of Material Science, 1990, 25(9): 3930−3937.

[15] CHUANG Chenghsin, HUANG Jongshin. Effects of solid distribution on the elastic buckling of honeycombs[J]. International Journal of Mechanical Sciences, 2002, 44(7): 1429−1443.

[16] KIM H S, AL-HASSANI S T S. A morphological elastic model of general hexagonal columnar structures[J]. International Journal of Mechanical Sciences, 2001, 43(4): 1027−1060.

[17] LI K, GAO X L, ROY A K. Micromechanics model for three-dimensional open-cell foams using a tetrakaidecahedral unit cell and Castigliano’s second theorem[J]. Composites Science and Technology, 2003, 63(12): 1769−1781.

[18] ZHU H X, MILLS N J, KNOTT J F. An analysis of the elastic properties of open-cell foams with tetrakaidecahedral cells[J]. Journal of the Mechanics and Physics of Solids, 1997, 45(3): 319−343.

[19] 刘培生. 三维网状泡沫金属杨氏模量和泊松比的数理表征[J].稀有金属材料与工程, 2009, 38(3): 240−244.

LIU Peisheng. Young’s modulus and poisson ratio of porous open-cell metal foams[J]. Rare Metal Materials and Engineering, 2009, 38(3): 240−244.

[20] 苏淑兰, 饶秋华, 贺跃辉. 新型Ti-A1金属间化合物多孔材料的弹性模量表征[J]. 粉末冶金材料科学与工程, 2012, 17(6): 804−809.

SU Shulan, RAO Qiuhua, HE Yuehui. Elastic modulus charaterization of new Ti-Al intermetallic porous material[J]. Materials Science and Engineering of Powder Metallurgy, 2012, 17(6): 804−809.

[21] SU Shulan, RAO Qiuhua, HE Yuehui. Theoretical prediction of effective elastic constants for new intermetallic compound porous material[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(4): 1090−1097.

(编辑 高海燕)

Theoretic characterization on poisson’s ratio characterization of new Ti-Al intermetallic porous material

SU Shulan1, RAO Qiuhua2, HE Yuehui3
(1. College of Civil Engineering and Mechanics, Central South University of Forestry & Technology, Changsha 410004, China; 2. School of Civil Engineering, Central South University, Changsha 410075, China; 3. Powder Metallurgy Research Institute, Central South University, Changsha 410083, China)

Based on pore spatial structure features of the new Ti-Al intermetallic porous material, a three-dimensional octahedral model was used to firstly deduce the calculation formula of its effective Poisson’s ratio by the energy method and an explicit expression between effective Poisson’s ratio and relative density was obtained. Meanwhile, the effect of cross-section shape and shear force of pore-edge on effective Poisson’s ratio was analyzed. Compared with the present calculation formulas of Poisson's ratio with circular cross-section pore-edge as an example, this result is more reasonable and reliable for porous material and the derivation process is more direct and effective for Poisson's ratio characterization by the energy method. The results show that the effect of cross-section shape and shear force increase with the increase of the relative density and the shear force of pore-edge must be considered if the relative density is larger.

Ti-Al intermetallic compound; porous material; octahedral model; energy method; Poisson’s ratio

TB383

A

1673-0224(2017)03-301-06

国家自然青年科学基金项目(11502307)；湖南省自然青年科学基金项目(2016JJ3187)；湖南省教育厅一般项目(14C1189)；中南林业科技大学引进高层次人才科研启动基金

2016−06−29；

2016−09−10

饶秋华，教授，博士。电话：0731-88877193；E-mail: raoqh@mail.csu.edu.cn