关于正则点的两个性质
2017-07-05广东省英德市西牛镇沙坝小学513028刘京培
中学数学研究(江西) 2017年7期
广东省英德市西牛镇沙坝小学 (513028) 刘京培
关于正则点的两个性质
广东省英德市西牛镇沙坝小学 (513028) 刘京培
文(1)给出了正则点的定义:在ΔABC中,若点Z满足AZ·BC=BZ·CA=CZ·AB,则此点称为正则点.

性质1 如图1,O、H、F、Z分别为ΔABC的外心、垂心、费马点和正则点,则有FZ∥OH.

图1
证:如图1,以AB为边向外作正ΔABM,顶点为M,连接CM,得C、F、M三点共线,且交OH于点P,连接OM交AB于点D,易得OM垂直平分AB,延长CZ
交OH于点Q,延长CH交AB于E.因为O、H互为等角共轭点,文[1]给出了F、Z互为等角共轭点,有∠BCO=∠ACH,∠BCZ=∠ACF,所以易得∠OCZ=∠HCF,∠OCF=∠HCQ.又CE⊥AB,OM⊥AB,得CE∥OM,∴∠HCF=∠OMC.




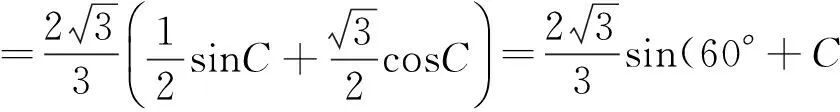

由等比性质知,FZ∥OH.
性质2 图与符号同上,若G为重心,则有

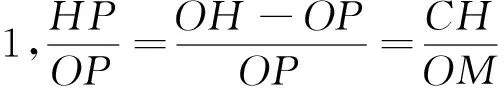
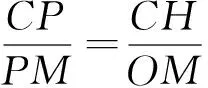





[1]沈文选,汤春桃.几何瑰宝[M].哈尔滨:哈尔滨工业大学出版社,2014:380-393.
