柯西不等式的多角度探索
2017-07-05河南省新蔡县第一高级中学463500李居之
河南省新蔡县第一高级中学 (463500) 李居之
柯西不等式的多角度探索
河南省新蔡县第一高级中学 (463500) 李居之
柯西不等式作为高中数学选修模块的内容,在解答一些不等式问题时,起到了举足轻重的作用.本文就从柯西不等式的角度去审视一些最值问题,供教师教学参考,加深学生对柯西不等式的理解.
例1 若等差数列{an}满足a21+a23=2,则a3+a4+a5的最大值为 .
这里给出两种解法.设此等差数列{an}的公差为d.

联想等差中项的性质,注意到3a3-a1=a3+2a3-a1=a3+a1+a5-a1=2a4,于是,又得到了一种更简易的解法.

上式两种解法都利用到了柯西不等式,且法二更令人耐人寻味,值得细细揣摩,是一道不可多得的好题.

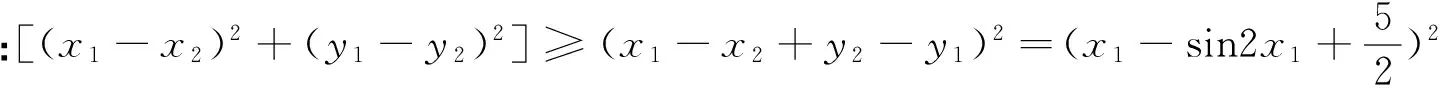
此题原法是数形结合找切线的斜率,但注意到(x1-x2)2+(y1-y2)2这种形式与柯西不等式类似,经过探究给出了新法.

此题的解法很多,但都需数形结合.基于柯西不等式将其化为代数问题,这种思路虽然一时难以想象,但更能加深学生对柯西不等式的理解,不失为一种好方法.
例4 设x,y为实数,若4x2+y2+xy=1,则2x+y的最小值为 .

例5 在平面直角坐标系中,设点P(x0,y0)到直线3x-4y-10=0与x=3的距离分别为d1、d2,若点P在单位圆x2+y2=1上运动,则5d1-d2的最大值为 .
解:因5d1-d2=|3x0-4y0-10|-|x0-3|≤
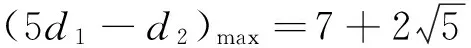
通过绝对值不等式的性质,再利用柯西不等式,降低了此题的难度;不过这需要判断两绝对值式子的符号,本文直接略去,读者可去尝试判断正负号,受到其中的启发.


此题是江苏的一道竞赛题,其解法较多,利用对称性x=y是本题的最优解法,但通过柯西不等式将x+y的值逼近出来,可能是试题的命题意向.
华罗庚说:“新的数学方法和概念常常比解决问题本身更重要.”运用柯西不等式需要一定的技巧性,不难掌握,容易理解,在解题过程中,是比较实用的方法.
