单一沙坝型海滩平衡剖面形态预测公式

匡翠萍，黄光玮，冒小丹，韩雪健，朱 磊

（1.同济大学土木工程学院，上海 200092；2.中交疏浚技术装备国家工程研究中心，上海 201208；3.河北省地质矿产勘查开发局第八地质大队，河北秦皇岛 066001）

离岸水下沙坝是海岸动力地貌中常见的一种形态，由波浪、潮流等海洋水动力综合作用堆积而成，常见于潮差小、潮流弱、波高小的低能海滩[1］，其不仅能削弱向岸波高、降低风暴潮等灾害的侵蚀，而且在潮流横向输沙作用下起到“喂养”海滩的作用。除自然形成的离岸沙坝，人工吹填的水下沙坝也作为一种海岸防护措施应用于海滩养护工程，如国内秦皇岛北戴河[2］和国外荷兰[3］等地实施的海滩养护工程中均采用了人工离岸沙坝，由于其具有对环境扰动小等特点，取代传统的水下防波堤等硬式建筑物以起到保护海滩的作用。

人工离岸沙坝的建设改变了原有的海滩地貌形态，分析和研究存在离岸沙坝的海滩剖面演变对海滩养护工程的设计优化和性能评估具有重要意义。Pan等[4］研究了2011—2014年秦皇岛西海滩养护后剖面形态演变，发现人工沙坝部分是剖面最活跃的部分，而剖面其他部分相对稳定，且在低能海滩中的离岸沙坝大致从对称向非对称发展。杨玉宝等[5］利用经验正交函数分析法（EOF法）得到分别对应平均海滩剖面、体积改变和形状改变的3个特征函数，探讨了含离岸沙坝的秦皇岛西海滩剖面演变模式。Kuang等[6］利用现场资料和数值模拟的方法研究山海关岸段海滩养护后人工沙坝的地形演变，发现人工沙坝对潮流的影响较小，但对波浪有明显的削弱作用；沙坝中的中粗砂在波浪作用下主要向岸移动，沙坝后方的岸线存在向海推进的趋势。

沙坝的形态演变最终会导致整个海滩剖面的变化。海滩剖面形态的拟合公式最先由Brunn[7］提出，基于丹麦、蒙特利湾和加利福尼亚三地实测数据提出了海滩平衡剖面公式（Equilibrium Beach Profile，EBP）；Dean[8］基于线性波浪理论和美国亚特兰大与墨西哥湾实测数据提出形式更简单的Dean公式；Bodge[9］、Larson[10］、Lee[11］和Dong[12］基于不同的理论提出各自的海滩平衡剖面公式，但上述公式主要适用于无沙坝的海滩剖面，当存在离岸单一型沙坝时无法较好地对沙坝形态进行描述，因此本文充分考虑近岸区域、沙坝形态和离岸区域差异，提出背景剖面—沙坝剖面模式的单一沙坝型海滩剖面形态预测公式。背景剖面指始终保持相对稳定的部分[13］，沙坝剖面在背景剖面的基础上发生横向移动和形态演变。将公式应用在戴河口至洋河口海滩修复工程岸段，计算剖面和实测剖面拟合较好，且成功应用于北戴河老虎石海滩和美国Fort Myers海滩，拟合效果均优于Stephens等[14］和Hsu等[15］所提出的公式，表明该公式能准确描述单一沙坝型海滩平衡剖面。

1 研究区域及养滩工程

北戴河新区戴河口至洋河口岸线整治工程以戴河口至仙螺岛约1.4km和洋河口至海上自助餐厅约1.0km两段为重点修复岸线，包括滩肩补沙、水下沙坝和人工岬头3项内容。滩肩补沙总方量约3×105m3，养滩沙中值粒径D50为0.19～0.41mm，补沙后滩肩高程达1.6m以上（85国家高程基准），沙滩宽度在原有基础上平均增加40～60m；在戴河口西侧导堤以南约100m和洋河口东侧导堤以东100m分别构建1座潜礁式人工岬头，岬头长约280～300m，宽度约12m，堤顶高程约-1.2m，2座岬头形成人工岬湾以降低海洋动力侵蚀；在离岸约250m处吹填3座人工沙坝，其中东北段设计2座、西南段设计1座，每座沙坝长约450m，坝顶宽约50m，底宽约80～100m，坝顶高程约-0.9m，吹填中值粒径D50为0.5～2.0mm的中粗沙，吹填方量约12×104m3，起到削减波浪和补充海滩沙源的作用。工程于2017年4月开始实施，2017年6月完工，工程示意如图1所示（坐标系统采用北京54坐标系，中央经度为120°）。

低能海滩是指波高常年较小、受风暴潮影响较小、破波带范围窄且靠近岸线、破波带地形演变较为缓慢的海滩[16］，北戴河戴河口至洋河口岸段属于低能海滩[17］。对低能海滩而言，波浪是影响泥沙输运和海滩侵蚀的主要因素[18］，在驱动和控制近岸地形上有重要作用[19-20］。为监测海域波浪情况，河北省地质矿产勘查开发局第八地质大队在戴河口ENE方向设立波浪测站（具体位置如图1），测站处水深约5～6m，监测频率为每小时1次。分析2016—2018年波浪实测资料并绘制波浪玫瑰图（如图2）知，2016年常浪向为SE向，总频率为16.79%，平均波高0.25m，强浪向为ENE向，频率为5.25%，平均波高0.58m。0～0.5m波级的出现频率为78.10%，0.5～1.0m波级出现频率为20.34%，1.0m以上波级出现频率为1.55%[21］。2017年常浪向为SSE向，总频率为20.74%，平均波高0.29m，强浪向为E向，频率为11.36%，平均波高0.34m；0～0.5m波级的出现频率为77.90%，0.5～1.0m波级出现频率为20.86%，1.0m以上波级出现频率为1.24%。2018年常浪向为SSE向，总频率为18.08%，平均波高0.28m，强浪向为ESE向，频率为15.23%，平均波高为0.29m；0～0.5m波级的出现频率为77.43%，0.5～1.0m波级出现频率为22.57%，1.0m以上波级出现频率为0.66%。总体而言，2016—2018年该区域波浪动力较弱，波向主要出现在ENE-SW方向，每年浪况较相似。

图2 波浪玫瑰图Fig.2 Diagram of wave rose

2 单一沙坝型海滩剖面演变

河北省地质矿产勘查开发局第八地质大队于工程前、后长时间对海滩剖面进行地形监测（剖面位置如图1所示），剖面高程以国家85高程为基准，离岸距离基点选择在相对固定且高程较高的位置，如浴场、护岸和海滨路上，以便对海滩养护区域进行连续、长期的岸滩监测。以N5、N6和N7存在单一沙坝的海滩剖面为例，分析含单一沙坝的海滩剖面演变特征。N5、N6和N7这3个剖面均取自养滩工程西南端的人工沙坝，养滩前和养滩后一年半内海滩剖面演变如图3。实线为2016年9月即养滩前海滩实测剖面，粗圆点为2017年6月即养滩竣工时的实测剖面，双点划线、虚线和细圆点分别为2018年3月、6月和9月海滩实测剖面。由图3（N6剖面缺少2018年9月实测数据）可知，吹填沙坝处为养滩剖面最活跃的位置，因入射波浪以向岸波浪为主，在波浪周期性作用下沙坝向海侧坡度逐渐平缓，沙坝坝顶处泥沙随波浪朝沙坝向岸侧区域运移，沙坝坝顶高程降低，向岸侧坡度趋于陡峭。离岸单一沙坝横向剖面形状向高度不对称趋势发展，这与Brutsche等[22］研究的含水下沙坝海滩所得结论一致。因沙坝泥沙的向岸横向输运和沙坝对滩肩回流的拦截作用，离岸单一沙坝朝向岸方向移动，此现象在N6和N7剖面较为明显，1年后坝顶位置分别向岸移动79m和72m。对比养滩工程后剖面可知，2018年6月之后离岸单一沙坝的海滩剖面形态已基本稳定，剖面变化较小，剖面坡度、面积和单宽体积相对稳定，可判断此时海滩剖面已基本达到平衡状态。

图1 戴河口至洋河口岸段海滩养护工程示意Fig.1 Beach nourishment project at the coast between the Daihe Estuary and the Yanghe Estuary

图3 含单一沙坝海滩实测剖面形态演变Fig.3 Morphological evolution of actual beach profile with a sandbar

3 单一沙坝型海滩平衡剖面公式

Brunn[7］对丹麦、蒙特利湾和加利福尼亚三地实测剖面数据进行分析，基于指数方法首先提出了海滩平衡剖面（EBP）公式；Dean[8］基于线性波浪理论与墨西哥湾和美国亚特兰大海滩剖面数据提出了著名且广泛认可的Dean公式，该公式形式简单，描述的剖面呈上凹和单调形态，但只通过一个单一粒径参数确定，无法反映动力和海岸的差异性；Bodge[9］和Larson[10］在Dean公式基础上改进并分别提出了指数经验公式和考虑不同泥沙粒径的EBP公式；Lee[11］则采用对数形式建立剖面形态参数。上述理论多是基于波能耗散和能量流转移理论建立，而长时间尺度的波浪条件通常考虑代表平均条件的高频波浪和代表极端条件的低频波浪，前者产生平衡剖面形态，后者则是剖面摄动条件。受动力条件、泥沙特性和地质条件等因素影响，很难建立一个基于过程的一般性长期平衡剖面公式。Dong[12］通过最大信息熵原理筛选出可能性最大的概率分布，建立海滩平衡剖面公式，如式（1）：

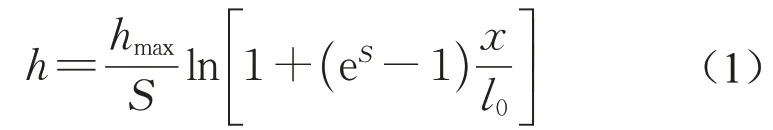
式中：hmax为剖面边缘水深；l0为水深hmax至0m高程处的水平距离；x为离岸距离；S为剖面形态参数，将泥沙粒径、沉降速度和长期波浪条件综合参数化，S=λ2hmax，参数λ2由约束条件得到。

文献[8-12］所建立的公式主要适用于无沙坝的海滩剖面，而对于存在离岸单一沙坝的海滩平衡剖面无法准确拟合。Wang和Davis[23］将存在离岸沙坝的海滩剖面分为内破碎区、岸侧沙坝斜坡区和近岸区3段区域，岸侧沙坝斜坡区通过线性插值较好地实现沙坝内外侧分离。Stephens等[14］提出五段式海滩剖面公式（简称Stephens公式），如式（2）所示：

式中：(xt，ht)为向岸侧沙槽坐标；(xc，hc)为沙坝坝顶处坐标；(xf，hf)为指数衰减剖面坐标；h∞为渐进水深；xm为向岸侧沙槽和沙坝之间的位置，xm=0.5(xt+xc)。该公式前4段采用抛物线形式描述沙坝及其向岸侧的剖面形态，最后一段采用指数形式描述向海侧的剖面形态，与Wang和Davis[23］提出的三段式公式相比，抛物线型公式拟合精度更高，更能反映海滩剖面弧度形态。

Tseng等[24］在Bodge[9］的指数经验公式中添加一项双曲线函数描述沙坝空间变化特性（式（3）），但该公式无法描述岸线附近的负水深（露滩情况），Hsu等[15］对该方程修正后得到精度更高的式（4）（简称为Hsu公式）：

式中：A1、A2、B1、B2和B3均为量纲一化的参数，可对实测数据进行最小二乘法拟合得到；X=x/xc和H=h/hc分别是量纲一化的离岸距离和水深，其中xc和hc分别为沙坝坝顶距岸线的水平距离和坝顶水深。

本文充分考虑剖面近岸和离岸区域差异，以背景剖面和沙坝剖面叠加建立单一沙坝型海滩平衡剖面形态公式，如式（5）所示：

式中：h0为背景水深，由对实测剖面资料拟合较好的Dong[12]公式（式1）计算（其中剖面边缘水深hmax取5.5m，剖面形态参数S取3.5）；沙坝剖面函数hbar采用两段式分段函数计算，见式（6）：

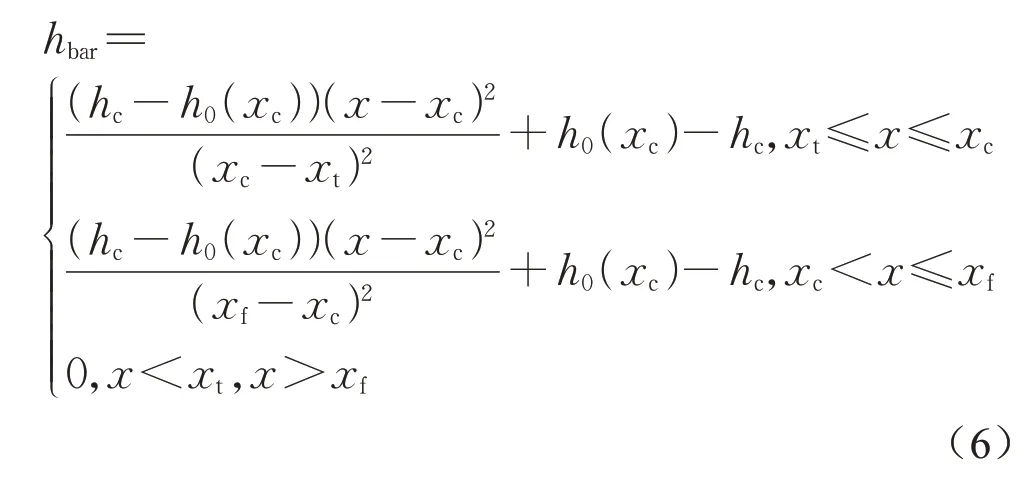
式中：h0(xc)为沙坝坝顶处的背景水深，由xc代入式（1）计算得到；xt和xf分别为沙坝向岸侧和离岸侧沙槽处的离岸距离，如无实测数据可由沙坝坝顶位置和沙坝底宽估算，可充分考虑沙坝的非对称性，各变量含义如图4所示。Stephens公式在已知或估算渐进水深条件下需确定(xt，ht)、(xc，hc)和(xf，hf)6个参数方可计算，而本文只需确定xc、hc、xt和xf4个参数便可计算，若知道沙坝宽度W，也可采用xc、hc和W这3个参数进行估算，通过对公式的简化和叠加计算将参数减少为4个或3个便可实现对存在离岸单一沙坝海滩平衡剖面的高精度拟合。

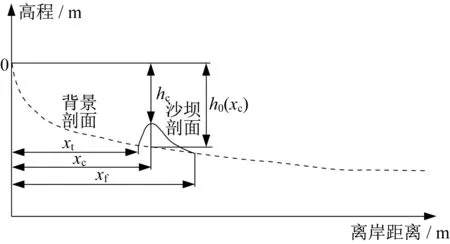
图4 单一沙坝型海滩剖面各变量示意Fig.4 Diagram of each variable in a single sandbar beach profile

4 单一沙坝型海滩平衡剖面公式的应用

选取戴河口至洋河口养护工程N5、N6和N7海滩实测数据（最后实测剖面）为参考的平衡剖面，采用Stephens公式（式（2））、Hsu公式（式（4））和本文所建立的公式（式（5））进行计算并与实测海滩剖面对比，计算结果如图5所示。由图5可知，Stephens分段函数的抛物线型公式对向岸侧沙坝拟合较好，但在向海侧沙坝和较远处离岸区域拟合结果较差，尤其在较远处离岸区域误差很大；Hsu公式在远海离岸区域剖面拟合较好，但受双曲函数的限制，无法描述沙坝的非对称性，特别是沙坝两侧沙槽处差异明显。相比之下，本文公式将含离岸单一沙坝的海滩剖面分成4段，分别为向岸侧沙槽至向岸区域、向岸侧沙槽至沙坝坝顶、沙坝坝顶至向海侧沙槽和向海侧沙槽至向海区域，此划分充分考虑剖面近岸、沙坝非对称性和离岸区域差异，可较好地对存在离岸单一沙坝海滩剖面进行描述，与实测海滩剖面最为符合，拟合精度均优于Stephens公式和Hsu公式。

图5 戴河口-洋河口海滩含沙坝平衡剖面对比Fig.5 Predicted equilibrium beach profiles compared with measured profile,Hsu’s and Stephens’s model between the Daihe Estuary and the Yanghe Estuary

为了阐明公式在低能海滩的适用性，选取秦皇岛北戴河老虎石海滩[25］和美国佛罗里达Fort Myers海滩[22］中存在离岸单一沙坝的典型剖面，采用Stephens公式、Hsu公式和本文提出的公式进行对比分析，老虎石海滩剖面L5和L13对比结果如图6所示，Fort Myers海滩的FMB32剖面如图7所示。由图可知，Hsu公式在沙槽处拟合较差，Stephens公式在离岸区域拟合较差，总体上看本文建立的公式拟合效果最佳，与前文所述一致，进一步说明了该公式能适用于低能海滩存在离岸单一沙坝型海滩平衡剖面的拟合，且拟合精度较高。

图6 老虎石海滩含沙坝平衡剖面对比Fig.6 Comparison of predicted equilibrium beach profiles against measured profile,Hsu’s and Stephens’s model at the Tiger-Rock Beach in Qinhuangdao

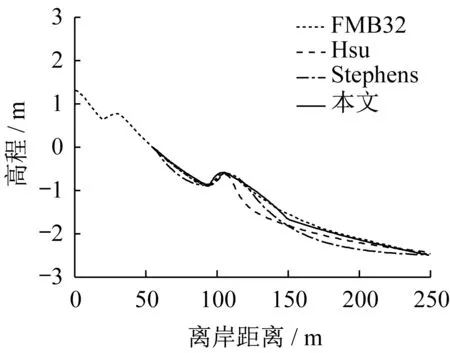
图7 Fort Myers海滩含沙坝平衡剖面对比Fig.7 Comparison of predicted equilibrium beach profiles against measured profile,Hsu’s and Stephens’s model at the Fort Myers Beach in Florida

5 结论

基于秦皇岛北戴河新区戴河口至洋河口海滩修复工程实测剖面数据，分析存在离岸单一沙坝的海滩平衡剖面形态演变，建立背景剖面与沙坝剖面叠加的单一沙坝型海滩平衡剖面形态预测公式，主要结论如下：

（1）离岸单一沙坝为海滩剖面最活跃的位置。波浪作用下沙坝向海侧逐渐趋于平缓，向岸侧趋于陡峭，沙坝坝顶高程降低，沙坝形态向高度不对称趋势发展；由于沙坝泥沙的向岸横向输运和沙坝对滩肩回流的拦截作用，沙坝整体有向岸移动的趋势；沙坝形态在海滩养护后1.0～1.5年趋于稳定，整个海滩剖面达到平衡状态。

（2）海滩养护后，离岸沙坝海滩剖面演变为背景剖面-沙坝剖面模式。背景剖面始终保持相对稳定，沙坝剖面在背景剖面的基础上发生横向移动和形态演变。

（3）本文提出背景剖面与沙坝剖面相叠加的单一沙坝型海滩平衡剖面形态公式，背景剖面基于最大信息熵原理充分考虑近岸侧和离岸侧差异，沙坝剖面采用3～4个参数以抛物线形式分段描述沙坝剖面，能较好地对存在离岸单一沙坝的海滩剖面进行拟合，并成功应用于北戴河老虎石海滩和美国佛罗里达Fort Myers海滩，且拟合精度优于Hsu公式和Stephens公式，该公式可用于低能砂质海滩中预测单一沙坝型海滩平衡剖面形态。对于存在多沙坝的海滩平衡剖面公式则有待进一步研究。

作者贡献声明：

匡翠萍：方法提出、论文撰写及论文修改。黄光玮：数据处理、论文初稿撰写。

冒小丹：数据处理、公式拟合。

韩雪健：数据处理。

朱 磊：现场工作。