《有心圆锥曲线的两个结论及应用》的注记
2017-07-05福建省龙岩第一中学364000胡寅年
中学数学研究(江西) 2017年7期
福建省龙岩第一中学 (364000) 胡寅年
《有心圆锥曲线的两个结论及应用》的注记
福建省龙岩第一中学 (364000) 胡寅年
贵刊文[1]虞懿、吴微庆老师的文章《有心圆锥曲线的两个结论及应用》,用传统的方法探索了张角是直角时椭圆、双曲线的一个几何性质,并例举了它们在求解高考压题中的应用.作为该几何性质研究的延续,本文运用三角函数的定义、平面几何知识与数形结合的思想方法去处理,思路将更加自然,结论将更加完备.
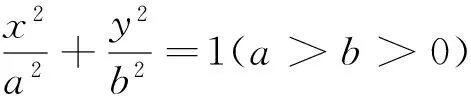
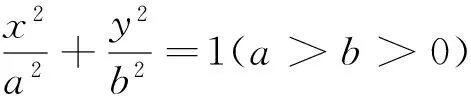

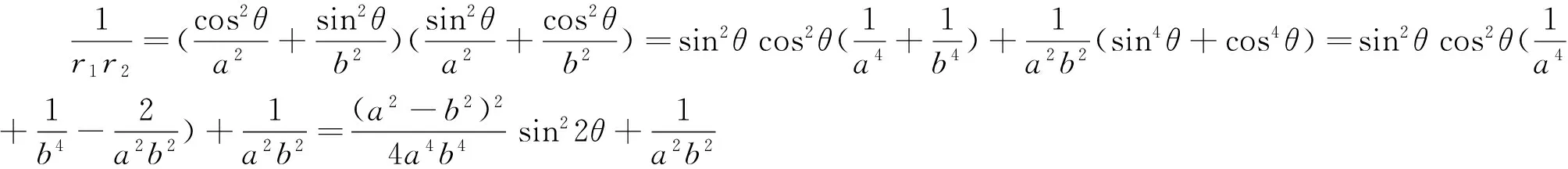
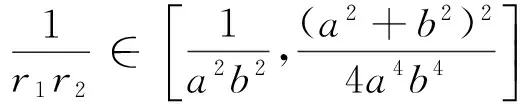
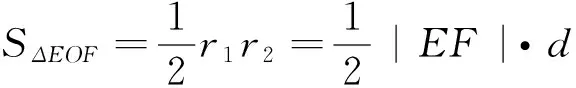
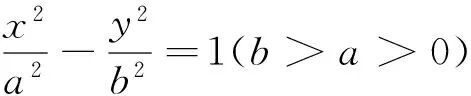
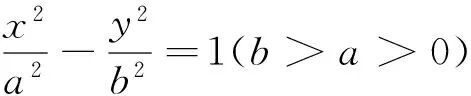

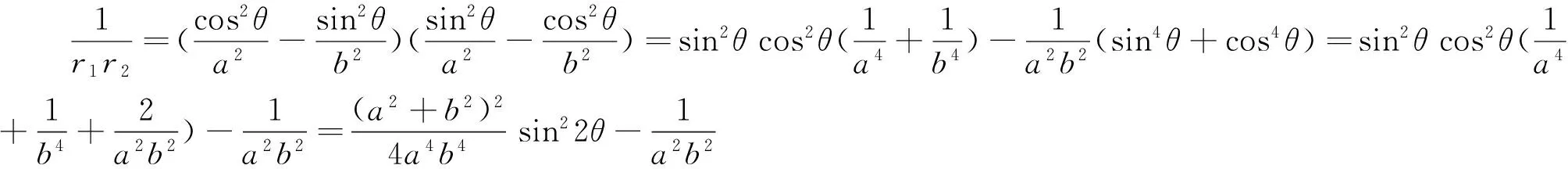

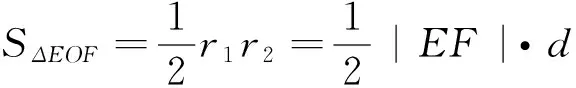
性质3 设E,F是抛物线y2=2px(p>0)上满足OE⊥OF的两个动点(O为坐标原点),则
(1)直线EF经过定点Q(2p,0);
(2)SΔEOF∈[4p2,+∞).

于是三点E、Q、F共线,即直线EF经过定点Q(2p,0).


∴(a2+b2)x2+2a2x+a2(1-b2)=0,
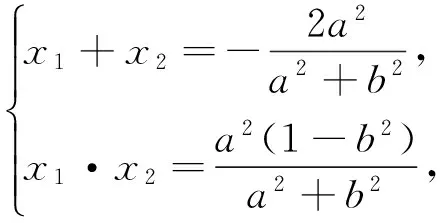
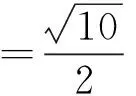
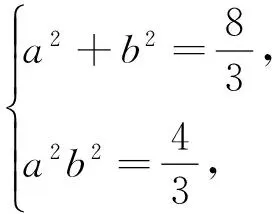
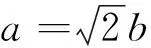
(2)设Q1、Q2为椭圆上的两个动点,OQ1⊥OQ2,过原点O作直线Q1Q2的垂线OD,垂足为D,求点D的轨迹方程.
简析:(1)略;
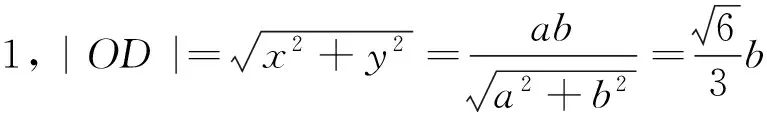
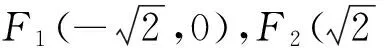
(1)求曲线Γ的方程;

(2)由已知条件可得四边形ACBD是一个菱形,于是四边形ACBD的周长=4|BD|,根据性质1,|BD|max=2,因此四边形ACBD的周长的最大值为8.
[1]虞懿,吴微庆.有心圆锥曲线的两个结论及应用[J].中学数学研究(江西),2016.8.
