“直观想象”在全国卷试题中的应用探析
2017-07-05福建省武平第一中学364300钟晓斌福建省漳州第一中学363000林新建
福建省武平第一中学 (364300) 钟晓斌福建省漳州第一中学 (363000) 林新建
“直观想象”在全国卷试题中的应用探析
福建省武平第一中学 (364300) 钟晓斌福建省漳州第一中学 (363000) 林新建
“直观想象”是高中数学核心素养的重要内涵.
“直观想象”是指借助几何直观和空间想象感知事物的形态与变化,利用图形理解和解决数学问题的过程.
“直观想象”主要包括:借助空间认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立形与数的联系;构建数学问题的直观模型,探索解决问题的思路.
以下以全国卷试题为例,就“直观想象”的解题应用作一探析,以飨读者.
1.在函数试题解答中的应用
运用“直观想象”策略,可以较好地引领图形特征的感知和形数关系的建立,使函数问题得以轻松解决.
例1 (2013年高考新课标卷Ⅰ理科16题)若函数f(x)=(1-x2)(x2+ax+b)的图像关于直线x=-2对称,则f(x)的最大值是 .
其实,若运用“直观想象”策略对函数的图形特征作感知,可将问题轻松予以解决,运算量也很小.
由“直观想象” 知函数f(x)有两个零点1,-1,而f(x)的图像关于直线x=-2对称,故f(x)另有两个零点-3,-5,所以f(x)=-(x-1)(x+1)(x+3)(x+5).
再运用“直观想象”对f(x)的图像作感知,可知若f(x)的图像向右平移两个单位,其最大值不会改变,于是我们可将求f(x)的最大值转化为求函数h(x)=-(x-3)(x-1)(x+1)(x+3)的最大值了.至此,直接配方即得f(x)=-(x2-5)2+16,故f(x)的最大值为16.
与高考参考解答比较,这样的解法另辟蹊径,轻松快捷,凸显了“直观想象”在引领图形特征感知、简化解题途径上的重要作用.

(1)求f(x)的解析式及单调区间;

解析:本题同样难在第(2)问,许多考生不知从何入手,望题兴叹而已.
其实,若能运用“直观想象”策略建立起形与数之间的联系,问题可轻松获得解决.
画出函数y=ex与y=(a+1)x+b的图像,由“直观想象”易知,要使上式恒成立,必须a+1>0,因此,要使(a+1)b最大,必须b>0.
又因为ex≥(a+1)x+b恒成立,再由“直观想象”可知,函数y=ex与y=(a+1)x+b的图像必须相切.
设切点为P(x0,y0),则y0=ex0=(a+1)x0+b,且ex0=a+1.
联立可得x0=ln(a+1),b=(a+1)-(a+1)ln(a+1),故(a+1)b=(a+1)2-(a+1)2ln(a+1).
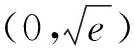
与高考参考答案比较,上述解法另辟蹊径、简洁优美,使我们感到:
(1)运用“直观想象”策略可轻松引领形数关系的建立,这样不但回避了分类讨论带来的麻烦,而且思维更加流畅、更容易接近问题的本质;
(2)思维的“拐点”,就是数学思想的“发源地”,数学解题要善于在思维的“拐点”处“直观想象”,往往会有“踏破铁鞋无觅处,柳暗花明又一村”的收获.
2.在三角试题解答中的应用
运用“直观想象”策略,可以较好地引领通法的运用和函数方程模型的构造,使三角问题得以轻松解决.

分析:本题仅知一边一角,因条件不足无法直接运用正、余弦定理予以求解,怎么办?
由“直观想象” 知,若引入新量(角或边),使得解三角形具备运用通法“知三求三”的条件,三角形方能予以求解!
同时,因为是最值求解问题,由“直观想象”知也必须引入变量,构造出待求最值关于这个变量的函数,问题方能求解.
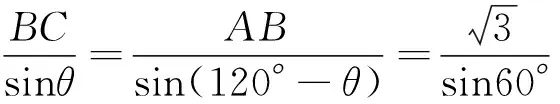
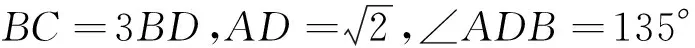
分析:本题也是三角形问题,无论在哪个三角形中,都是因为条件不足无法直接运用正、余弦定理予以求解,怎么办?
如同例3,由“直观想象”知:若引入新量(角或边),解三角形才能具备“知三求三”的条件,三角形方可解矣!
同时,因是求值问题,由“直观想象”知,也必须设出变量,构建出关于待求变量的方程,进而通过解方程方能将问题解决.

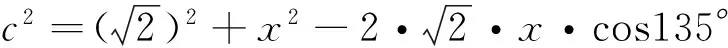
3.在数列试题解答中的应用
运用“直观想象”策略,可以较好地引领求和模型的构造和变化规律的预测,使数列问题得以轻松解决.
例5 (2014年高考全国卷Ⅱ理科17题)已知{an}满足a1=1,an+1=3an+1.
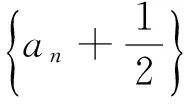
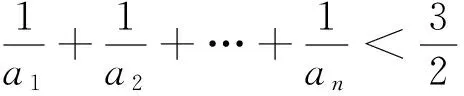
分析:本题难在第(2)问,直接证明无从下手.
例6 (2012年高考全国新课标卷理科16题)数列{an}满足an+1+(-1)nan=2n-1,则{an}的前60项和为 .
分析:本题是填空把关题,依常规方法求解极为繁琐.其实,由“直观想象”不难预知,本题是填空题,故不论数列{an}如何变化,其前60项的和不会因数列的变化而变化,由此我们可将首项特殊化予以求解.
解析:由an+1+(-1)nan=2n-1,得an+1=2n-1-(-1)nan.令a1=1,则有a2=2,a3=1,a4=6,a5=1,a6=10,a7=1,a8=14,…
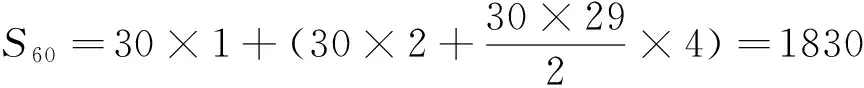
评析:上述求解轻松快捷,不亦乐乎,这得益于首项的特殊化,否则规律不易探明,求解势必复杂耗时.而想到运用“特殊化”策略予以求解,这又取决于对数列变化规律的“直观想象”,凸显了“直观想象”在预测数列问题的变化规律上的重要作用.
4.在解几试题解答中的应用
运用“直观想象”策略,可以较好地引领图形的运用和问题的转化,使解几问题得以轻松解决.
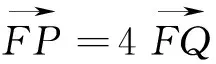
分析:本题依常规方法求解较为麻烦,若运用“直观想象”策略对图形作考察,问题即可转化,答案瞬间可得.

A.a2+b2≤1B.a2+b2≥1
解析:本题直接求解无从下手,若运用“直观想象”策略对图形作考察,问题即可转化,求解轻松快捷.
“直观想象” 在数学解题中有着重要的作用,在直观想象核心素养的形成过程中,学生能够进一步发展几何直观和空间想象能力,增强运用图形和空间想象思考问题的意识,提升数形结合的能力,感悟事物的本质,培养创新思维,平时教学和高考复习都应予以足够的重视.
