具有表面效应的压电半空间中的表面波1)

周伟建 陈伟球

(浙江大学工程力学系，杭州310027)

(浙江大学流体动力与机电系统国家重点实验室，杭州310027)(浙江省软体机器人与智能器件研究重点实验室，杭州310027)

具有表面效应的压电半空间中的表面波1)

周伟建 陈伟球2)

(浙江大学工程力学系，杭州310027)

(浙江大学流体动力与机电系统国家重点实验室，杭州310027)(浙江省软体机器人与智能器件研究重点实验室，杭州310027)

纳米科技的快速发展使压电纳米结构在纳米机电系统中得到广泛应用，形成了诸如纳米压电电子学等新的研究方向.与传统的宏观压电材料相比，在纳米尺度下压电材料往往呈现出不同的力学特性，而造成这种差异的原因之一便是表面效应.本文基于Stroh公式、Barnett-Lothe积分矩阵及表面阻抗矩阵，研究计入表面效应的任意各向异性压电半空间中的表面波传播问题，导出了频散方程.针对横观各向同性压电材料，假设矢状平面平行于材料各向同性面，发现Rayleigh表面波和B-G波解耦，并得到各自的显式频散方程.结果表明，Rayleigh表面波的波速小于偏振方向垂直于表面的体波，而B-G波的波速小于偏振方向垂直于矢状平面的体波.以PZT-5H材料为例，用数值方法考察表面残余应力和电学边界条件对表面波频散特性的影响发现：表面残余应力只对第一阶Rayleigh波有明显的影响；电学开路情形的B-G波比电学闭路情形的B-G波传播快.本文工作可为纳米表面声波器件的设计或压电纳米结构的无损检测提供理论依据.

表面波，表面效应，压电材料，Stroh公式，频散关系

引言

由于具有优良的力电耦合效应，压电纳米线、纳米梁和纳米板等压电纳米结构已应用于纳米机电耦合系统，比如滤波器、传感器、发电机和压电场效应晶体管等[14].与传统的宏观压电材料[5]相比，纳米尺度下压电材料往往具有不同的物理性质，特别是呈现明显的尺寸效应[67].对材料性能或结构响应具有尺寸依赖性的解释很多[811]，其中之一便是表面效应.

表面效应一般包括表面异质性和表面残余应力对体材料的影响.表面异质性是指由于所处的环境不同，物体表面或表面附近的原子排列方式与物体内部的原子排列方式不同，从而使表面层与物体内部具有不同的物理性质.在宏观尺度，表面积与体积之比非常小，表面异质性的影响一般可忽略.然而，随着表面积与体积之比增大，比如在纳米尺度，表面异质性对力学响应的影响常常就需要予以考虑[12].此外，材料的制备工艺或表面本身的驰豫会导致表面残余应力，而残余应力也对纳米材料的力学响应有重要影响[13-14].

对于弹性材料，Gurtin和Murdoch[15]建立了表面弹性理论(即G-M理论)，将弹性体表面异质层及残余应力的影响等效为非经典边界条件，从而避免了对表面异质层的直接分析，简化了问题的研究.最近，Chen等[16]基于状态空间法建立了各向异性圆柱的表面弹性理论，并用于研究纳米尺度圆柱中轴对称波的传播.对于压电材料，Huang和Yu[17]推广GM理论，建立了表面压电理论(即H-Y理论)，给出了考虑表面效应的等效边界条件.H-Y理论已被大量应用于压电纳米材料/结构的静/动力学响应研究中，如Yan和Jiang[1820]分析了表面效应对压电纳米线、压电纳米梁以及纳米曲梁的静/动力学响应的影响；Zhang等[21]考察了压电纳米板中的反平面剪切波；最近，Zhang等[22]研究了压电纳米板中Lamb波的传播特性.

相较于对压电纳米线、梁和板静动力响应的研究，对考虑表面效应的压电半空间中表面波传播特性的研究尚少.Chen[23]基于状态空间列式方便地建立了平表面的表面压电理论，并研究了表面效应对Bleustein-Gulyaev(B-G)波[2425]传播特性的影响.该工作局限于横观各向同性压电材料，并且只研究了B-G波.本文基于H-Y表面压电理论，利用Stroh公式[2627]，Barnett-Lothe积分矩阵[28]及表面阻抗矩阵[2931]，建立了计入表面效应的任意各向异性压电材料的表面波频散方程.针对各向同性面与矢状平面平行的横观各向同性压电半空间，得到了解耦的Rayleigh表面波和B-G波的显式频散方程.最后用数值方法考察了表面残余应力和电学边界条件对Rayleigh波和B-G波的频散特性的影响.

1 基本方程

针对具有表面效应的压电半空间，建立右手笛卡尔坐标系，使x1和x3轴位于表面上，x2轴正方向指向半空间内部.对于半空间，本构方程为[32-33]

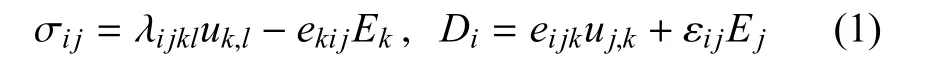
其中，下标逗号代表对坐标求导(即ui,j=∂ui/∂xj)，σij,ui,Ei和Di分别为应力、位移、电场强度和电位移，λijkl,ekij和εij分别为弹性刚度系数、压电应力系数和介电常数，并满足如下对称性

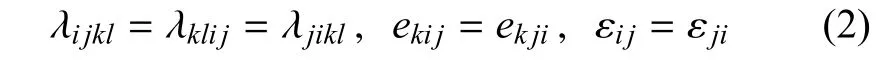
若未明确说明，本文小写拉丁字母下标取值1,2,3，大写拉丁字母下标取值1,2,3,4，希腊字母下标取值为1或3，而重复下标代表求和.

不计体力和自由电荷，则半空间内任一点的运动微分方程和电荷方程分别为

其中,ρ为密度.对于压电表面，根据H-Y理论，有如下本构方程[17]

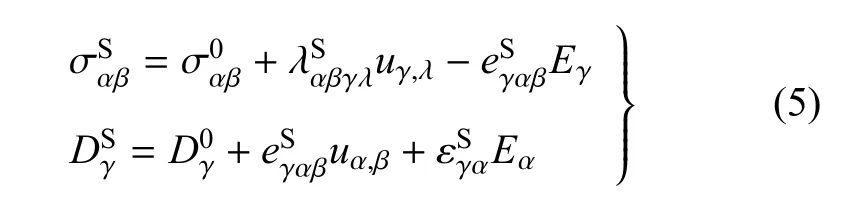
压电表面的力平衡微分方程为[22]

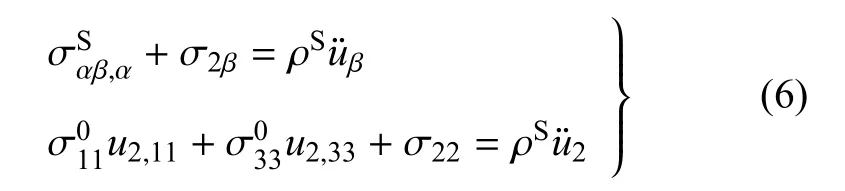
将式(5)代入式(6)，可得如下等效力学边界条件

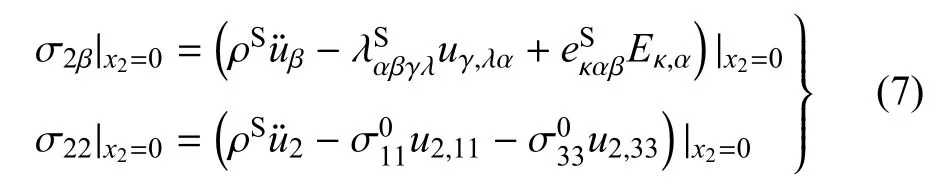
考虑两种电学边界条件，即电学开路和电学闭路.若表面电学开路，则有[22]

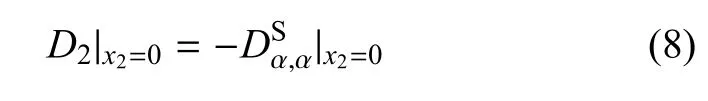
将式(5)代入式(8)，可得开路时的等效电学边界条件为

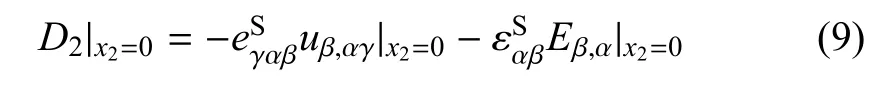
若表面电学闭路，则有[21]

其中,φ为电势，且有E1=-φ,1且E3=-φ,3.

2 各向异性压电弹性体的表面波

2.1 Stroh公式

考虑与x3坐标无关并以波速v沿x1方向传播的平面波

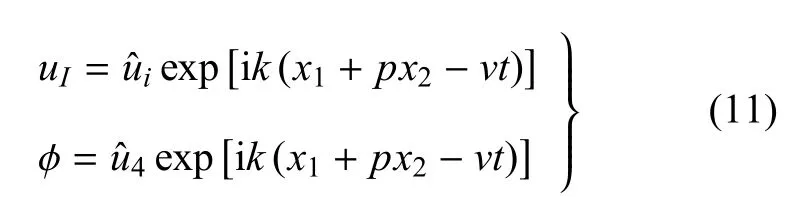
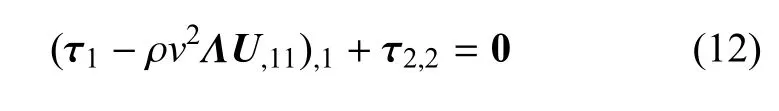
其中,U=[u1u2u3φ]T为广义位移(上标T代表矩阵转置)，Λ =diag[1,1,1,0]；τ1为 x1(常数)面上的广义应力，τ2为x2(常数)面上的广义应力，即

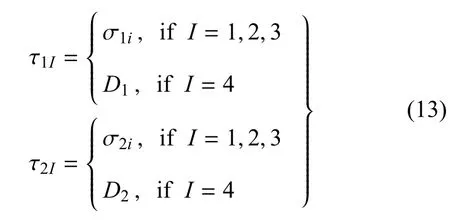
引入应力势矢量f

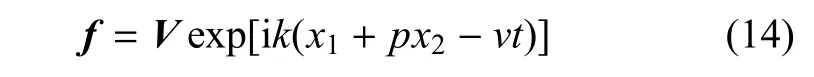
使得

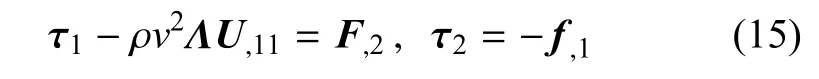
则方程(12)自动满足.

进一步将本构方程(1)代入式(15)，可得

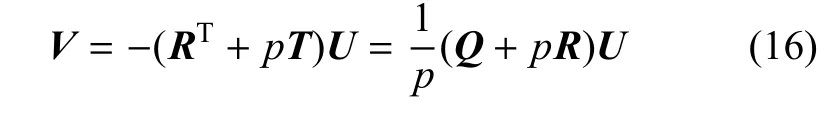
其中

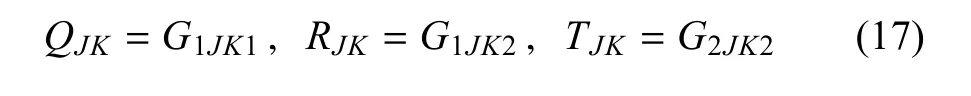
而GiJKl为广义动力学弹性张量，定义如下[28]

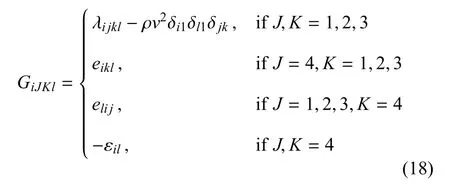
其中,δkl为克罗内克符号.

将式(16)的两个等式合写为如下特征值方程

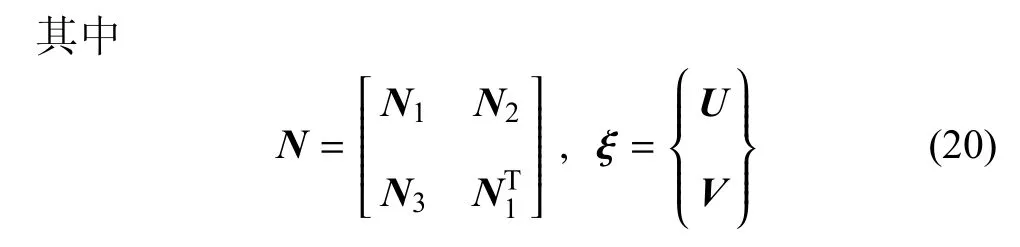
分别为广义基本弹性张量和状态矢量ξ，且

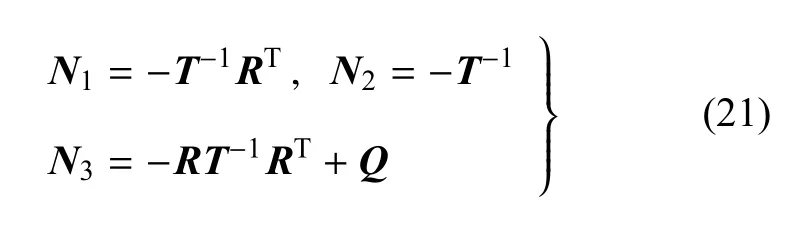
2.2 Barnett-Lothe积分矩阵及表面阻抗矩阵

如将坐标系以x3为轴旋转θ角度得到新的坐标系，重新建立类似式(19)的特征值方程

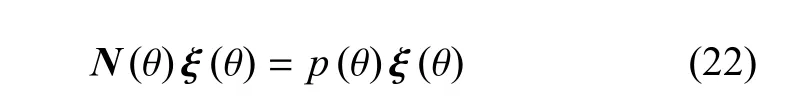
其中

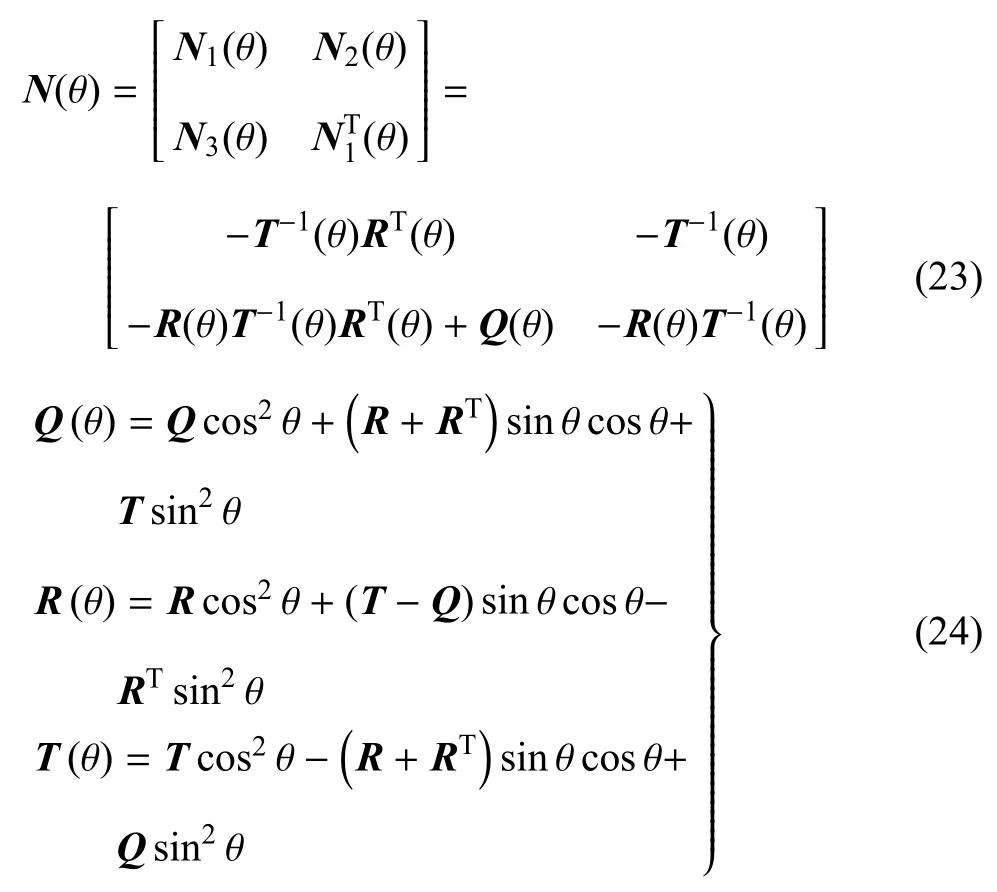
当波速v小于某一临界波速vL时，对于任意θ，N(θ)总有4对共轭复特征值和 4对共轭复特征矢量；当波速大于临界波速vL时，其中一对或多对共轭特征值会转变为一对或多对相反实特征值.

当波速 v小于临界波速 vL时，令 pI(θ)(I=1,2,3,4)为 N(θ)的虚部为正的4个特征值，另外4个特征值为pI+4(θ)=(θ)，这里顶标“– ”代表复共轭.特征值 pI(θ)对应的特征矢量为 ξI(θ).当波速大于临界波速 vL时，取 pI(θ)(I=1,2,3,4)为 N(θ)的虚部为正或正实数的4个特征值.需要指出，虚部为正的特征值对应沿厚度方向衰减的偏振波，而实特征值对应不衰减的体偏振波.

定义压电材料的Φ型表面阻抗矩阵MΦ如下[28]

其中

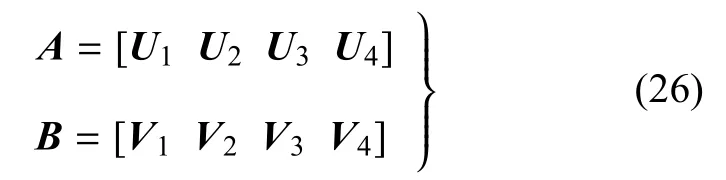
因此，广义位移偏振矢量UI(I=1,2,3,4)和广义应力势偏振矢量VI可通过阻抗矩阵相联系，即VI=-iMΦUI.当波速v＜vL时，MΦ也可由积分矩阵S和H计算得到[28]

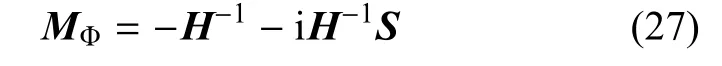
其中

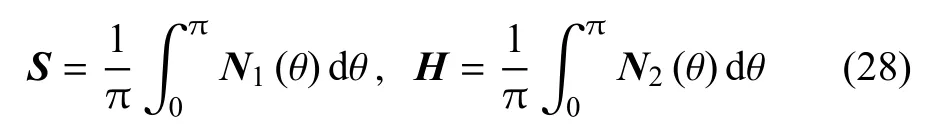
当边界由应力和电位移表示时(如表面应力自由且电学开路)，基于Φ型表面阻抗矩阵MΦ的计算将较为方便；而当边界由应力和电势表示时(如表面应力自由且电学闭路)，则用按如下定义的F型表面阻抗矩阵计算更方便[30]

其中

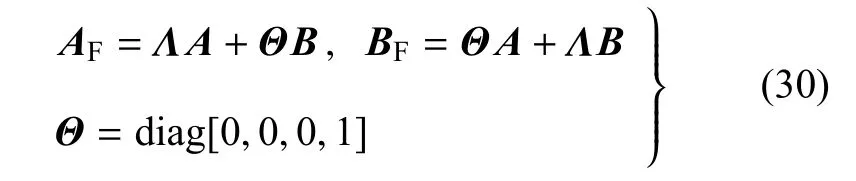
根据Lothe和Barnett[30]的研究，Φ和F型表面阻抗矩阵具有如下性质：

(1)当0≤v＜vL时，MΦ和MF都为厄密共轭矩阵，它们的特征值都是实数;

(2)当0≤v＜vL时,MΦ和MF的特征值都是速度v的单调递减函数;

(3)速度为零(v=0)时，MΦ有3个正特征值和1个负特征值，而MF有4个正特征值;

(4)MF44＞0且当v=vL时MF44为有限值，因此当v=vL时MF44至少有一个正特征值;

(5)MΦ和MF之间具有如下转换关系

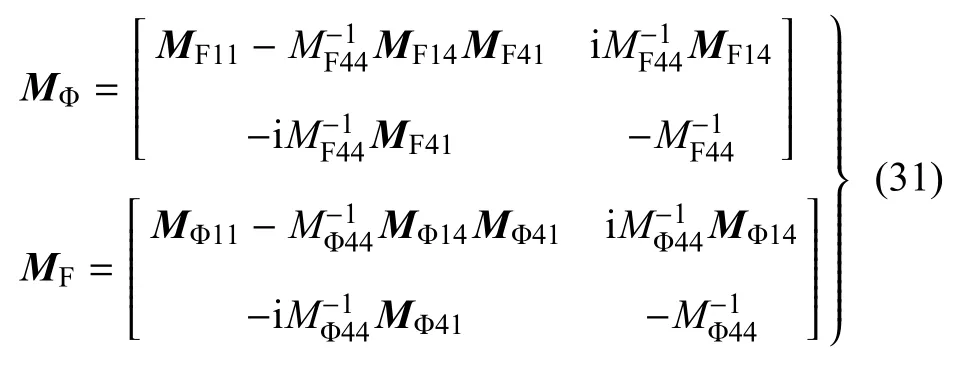
式(31)中，1是1,2,3的缩写，比如MΦ11代表矩阵MΦ的左上3×3子矩阵.

2.3 表面波的频散方程

考虑沿x1方向传播并沿x2方向衰减的广义二维表面波，此时广义位移、广义应力势矢量为广义基本弹性张量N的特征矢量ξI(I=1,2,3,4)的线性叠加

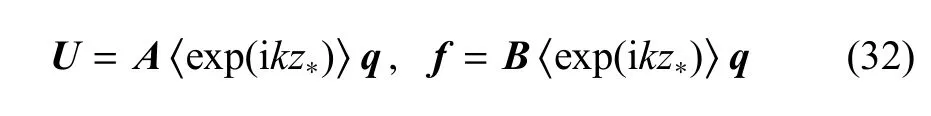
其中,qI为待定系数，并且

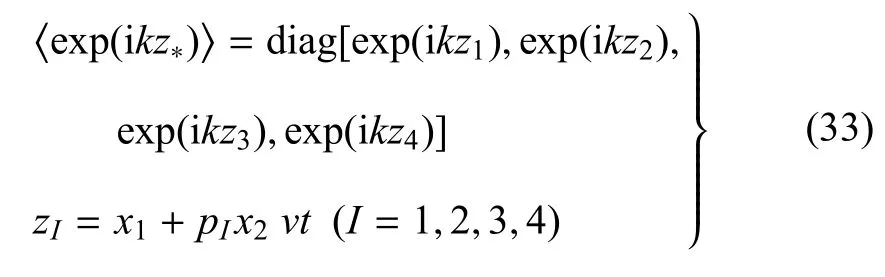
结合式(15)和式(32)可得

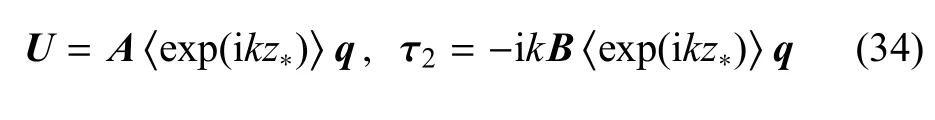
首先考虑表面应力自由且电学开路的情形.将上式代入等效边界条件(7)和条件(9)，可得

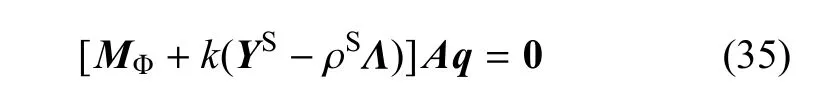
其中

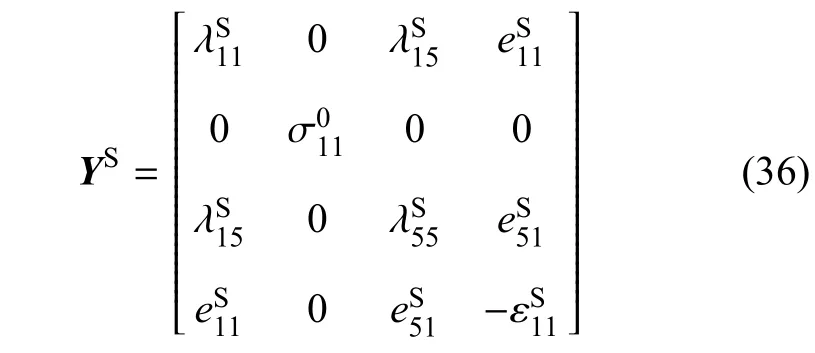
要使方程(35)有非零解，其系数矩阵行列式须为零

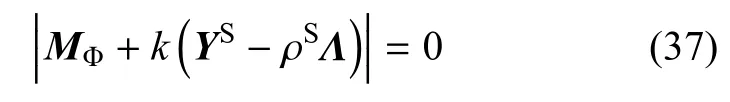
上式即应力自由且电学开路情形下的表面波频散方程.

其次考虑表面应力自由且电学闭路的情形.由式(34)可得

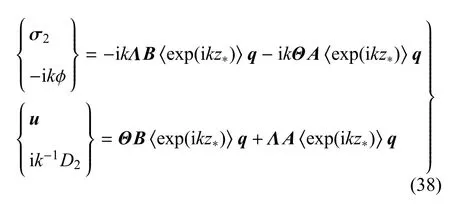
其中,u为机械位移矢量，σ2=[σ21σ22σ23]T.由等效边界条件(7)和条件(10)可得

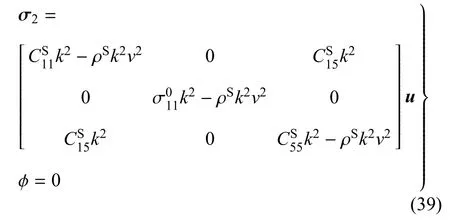
结合式(38)和式(39)有

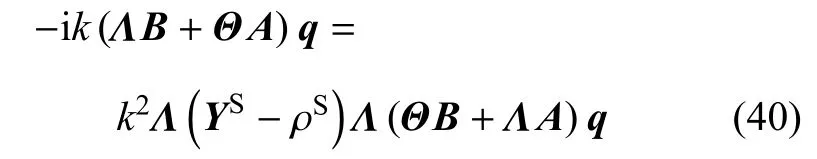
利用式(30)和F型阻抗矩阵的定义，上式可写为

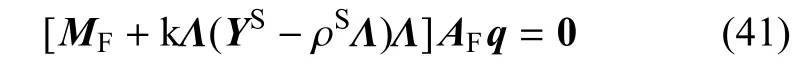
有非零解的条件为

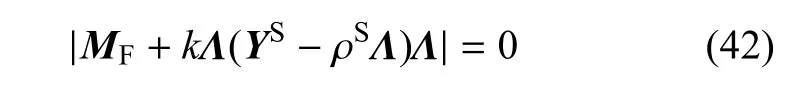
上式即应力自由且电学闭路情形下的表面波频散方程.

3 横观各向同性压电材料中的表面波

本节考虑以x1-x2平面为各向同性面的横观各向同性材料.N的特征值pI(I=1,2,3,4)和对应的特征矢量ξI为[34]

并且V2＜V1.需要指出的是，Vi(i=1,2,3)为偏振方向为xi的体波波速.

由特征矢量(43)可得Φ型表面阻抗矩阵MΦ的解析表达式

利用Φ型和F型阻抗矩阵间的转换关系式(31)，可得

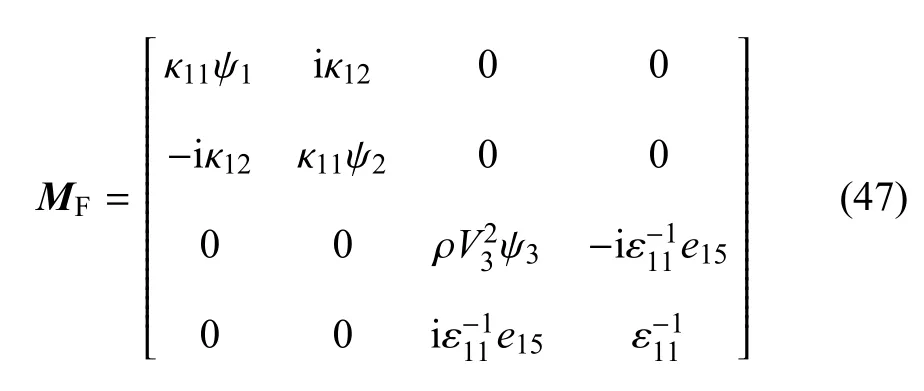
假设表面参数是对应体参数的标量倍[21]，即

其中,上标B代表体参数，l0为材料内禀尺度.这样，对于横观各向同性压电材料，有

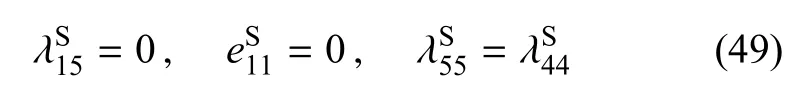
将式(49)代入式(36)，得

将式(45)和式(50)代入式(37)可得表面应力自由且电学开路的表面波频散方程

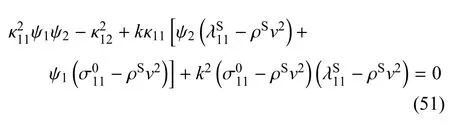
及

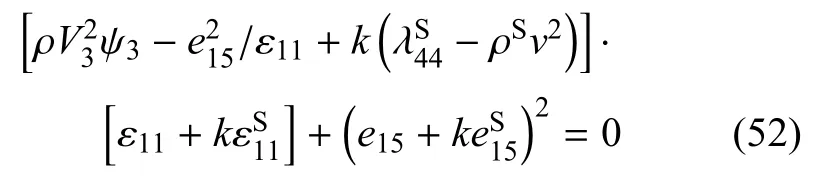
式(51)为Rayleigh表面波的频散方程，而式(52)为B-G波的频散方程.若不计表面效应，则式(52)退化为

容易知道上式的解为体波波速；所以，若没有表面效应，表面应力自由且电学开路的压电半空间不存在B-G波.

将式(47)和式(50)代入式(42)可得表面应力自由且电学开路的Rayleigh表面波和B-G波的频散方程.Rayleigh表面波的频散方程依然为式(51)，即Rayleigh波不受表面电学边界条件的影响，而B-G波的频散方程则变为

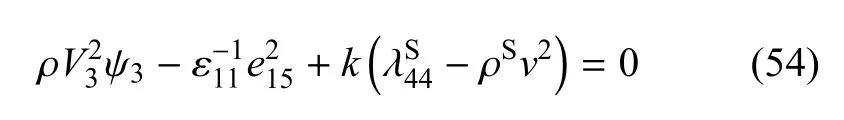
若忽略表面效应，则式(54)退化为

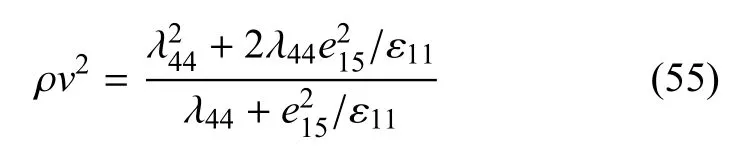
上式与电学闭路时的经典B-G波频散方程[24]完全一致.

需要指出，当式(51)成立时，位移场为

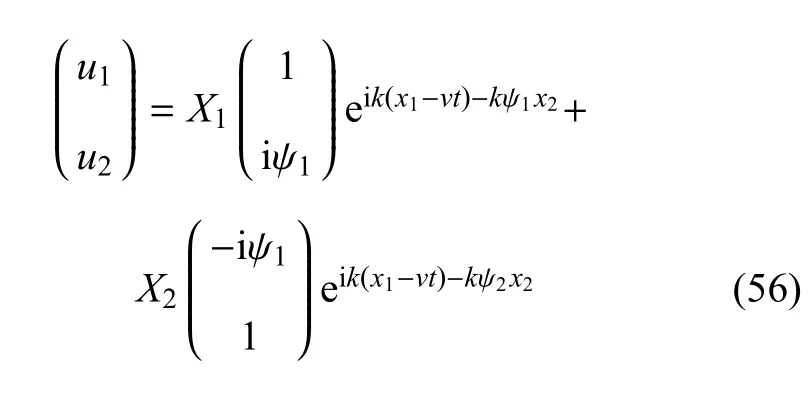
其中，X1和X2为待定系数.要使式(56)为Rayleigh表面波解，即能量聚集于表面附近而不泄露，则需v＜V2.

当式(52)或式(54)成立时，位移场为

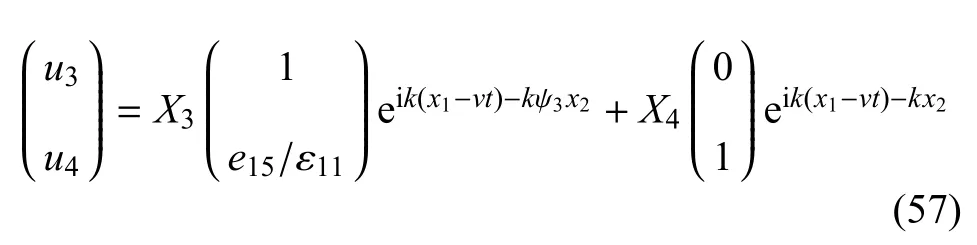
其中，X3和X4为待定系数.要使得式(57)为B-G波解，则需v＜V3.所以，Rayleigh波的波速范围为0＜v＜V2，而B-G波的波速范围为0＜v＜V3.特别地，B-G波的频散方程(52)和方程(54)显示表面残余应力对B-G波无影响.

4 数值算例

设压电半空间材料为 PZT-5H，其材料常数为[35]：λ11=126GPa，λ12=79.5GPa，λ44=23GPa，e15= 17C/m2，e31= -6.5C/m2，ε11= 1500 ×10-11F/m，ρ=7500kg/m3.对于压电表面，采用Huang和 Yu[17]给出的值：=7.56N/m，=-3×10-8C/m，σ=1N/m.另外，取 ρS=7.5×10-6kg/m2[21]，而其他表面参数按如下方式取值[22]

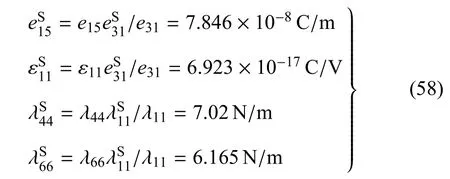
图1为Rayleigh表面波的频散曲线，其横坐标为无量纲波数κ=kl0(设内禀尺寸l0=1nm)，纵坐标为无量纲波速v0=v/V2.由图1可见二阶Rayleigh表面波：第一阶Rayleigh波(即FRW)和第二阶Rayleigh波(即SRW，也称为Sezawa波[36])，并且随着波长的减小或内禀尺度的增大,它们的波速都减小.在长波范围内，只有FRW可传播；当波数大于某一临界值后，也能传播SRW.还可观察到表面残余应力能提高Rayleigh波的波速，其中FRW对残余应力更加敏感，而Sezawa波则几乎不受影响.

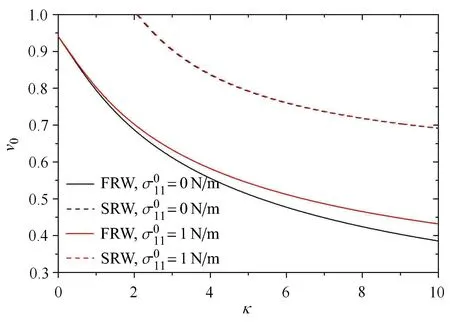
图1 Rayleigh表面波的频散曲线Fig.1 Dispersion curves of Rayleigh waves

图2为B-G波的频散曲线，其中黑色线对应电学开路，而红色线对应电学闭路.随着波数的增大或内禀尺度的增大，B-G波波速减小.在波数为零时，电学开路情形下无驻波形式的B-G波，而在电学闭路情形下B-G波以波速vBG＜V3传播.电学开路情形的B-G波波速大于电学闭路情形的B-G波波速，且随着波数的增大或内禀尺度的增大,两者之间的差别增大.特别地，正如第3节所指出的，B-G波的波速大于体波波速V2而小于体波波速V3.

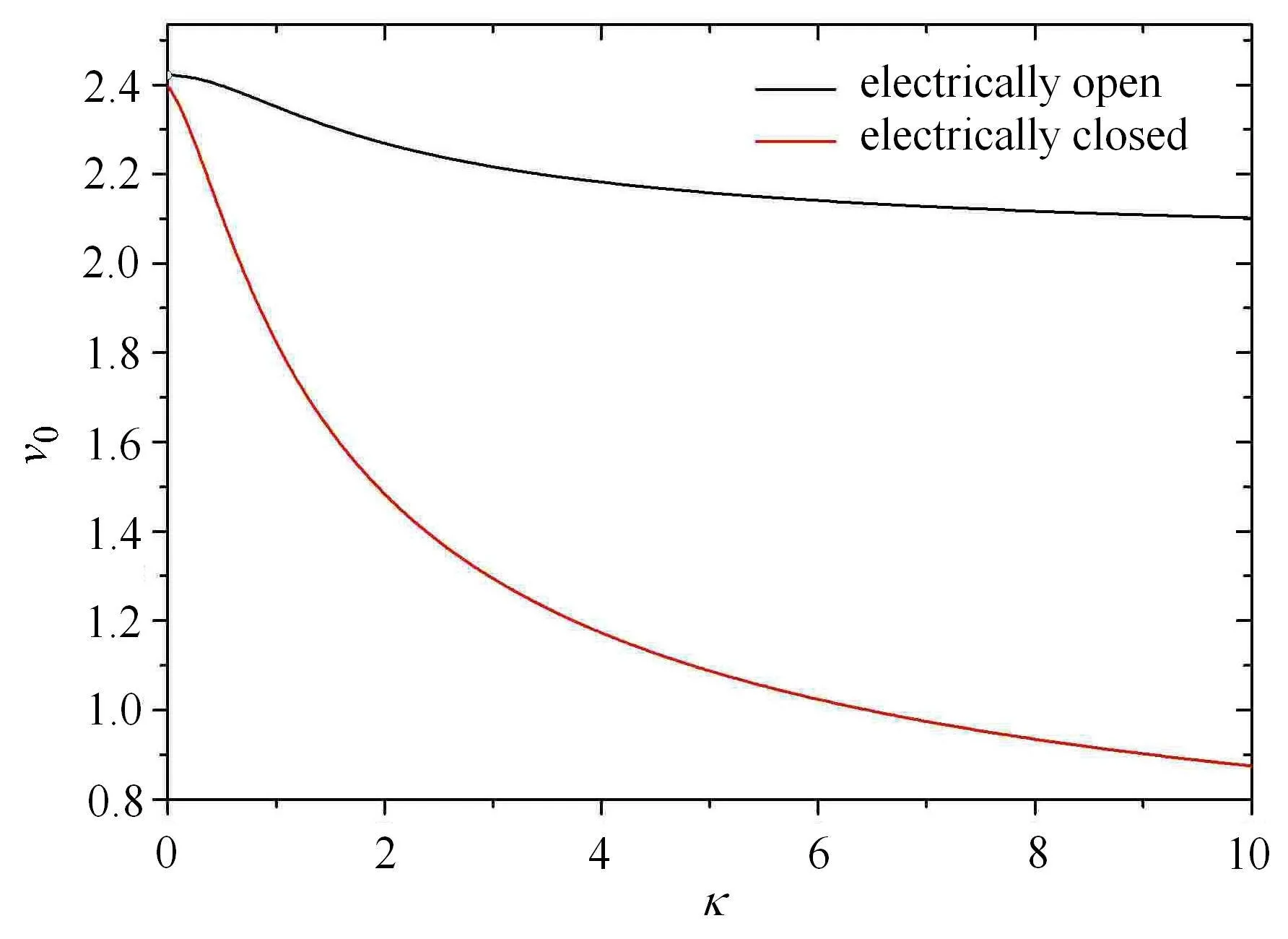
图2 B-G波的频散曲线Fig.2 Dispersion curves of B-G waves

5 结论

基于Stroh公式和表面阻抗矩阵建立了考虑表面效应的任意各向异性压电半空间表面波的控制方程.以横观各向同性压电材料为例，得到了Rayleigh波和B-G波的频散方程，形式简洁.分析表明，对于横观各向同性压电材料，当矢状平面平行于材料各向同性面时，电学边界条件对Rayleigh表面波无影响，Rayleigh波波速小于x2方向体波波速V2，而B-G波波速小于x3方向的体波波速V3.数值结果表明：(1)随着波数的增大或内禀尺度的增大，表面效应增强，表面波波速减小；(2)表面残余应力使Rayleigh波波速增大，且表面残余应力对第一阶Rayleigh波影响明显，而对第二阶Rayleigh波(即Sezawa波)影响甚微；(3)电学边界条件对B-G波有明显影响：电学开路情形的B-G波比电学闭路情形的B-G波传播快，而且随着表面效应的增强(波数增大或内禀尺度增大)，两者传播速度之间的差别将拉大.本文所建立的考虑表面效应的任意各向异性压半空间表面波的理论研究框架以及所得到的理论和数值结果有助于深入理解纳米尺度的表面波特性，可为纳米声波器件的设计提供思路，并为压电纳米结构的无损检测提供理论依据.

1 Fang XQ,Liu JX,Gupta V.Fundamental formulations and recent achievements in piezoelectric nano-structures：A review.Nanoscale,2013,5(5)：1716-1726

2 Voon LC,Willatzen M.Electromechanical phenomena in semi-conductor nanostructures.Journal of Applied Physics,2011,109：031101

3 Lao CS,Kuang Q,Wang ZL.Polymer functionalized piezoelectric-FET as humidity/chemical nanosensors.Applied Physics Letters,2007,90(26)：262107

4 Wang XD,Zhou J,Song JH,et al.Piezoelectric fiele ff ect transistor and nanoforce sensor based on a single ZnO nanowire.Nano Letters,2006,6(12)：2768-2772

5孔艳平,刘金喜.PMN-PT层/弹性基底结构中声表面波特性分析.力学学报,2015,47(3)：493-502(Kong Yanping,Liu Jinxi.Surface acoustic wave propagation in the PMN-PT layer/elastic substrate.ChineseJournalofTheoreticalandAppliedMechanics,2015,47(3)：493-502(in Chinese))

6 Stan G,Ciobanu CV,Parthangal PM,et al.Diameter-dependent radial and tangential elastic moduli of ZnO nanowires.Nano Letters,2007,7(12)：3691-3697

7 Chen CQ,Shi Y,Zhang YS,et al.Size dependence of Young’s modulus in ZnO nanowires.Physical Review Letters,2006,96(7)：075505

8徐巍,王立峰,蒋经农.基于应变梯度中厚板单元的石墨烯振动研究.力学学报,2015,47(5)：751-761(Xu Wei,Wang Lifeng,Jiang Jingnong.Finite element analysis of strain gradient middle thick plate model on the vibration of graphene sheets.Chinese Journal of Theoretical and Applied Mechanics,2015,47(5)：751-761(in Chinese))

9唐宇帆,任树伟,辛锋先等.MEMS系统中微平板结构声振耦合性能研究.力学学报,2016,48(4)：907-916(Tang Yufan,Ren Shuwei,Xin Fengxian,et al.Scale e ff ect analysis for the vibroacoustic performance of a micro-plate.Chinese Journal of Theoretical and Applied Mechanics,2016,48(4)：907-916(in Chinese))

10陈玲,沈纪苹,李成等.梯度型非局部高阶梁理论与非局部弯曲新解法.力学学报,2016,48(1)：127-134(Chen Ling,Shen Jiping,Li Cheng,et al.Gradient type of nonlocal higher-order beam theory and new solution methodology of nonlocal bending deflection Chinese Journal of Theoretical and Applied Mechanics,2016,48(1)：127-134(in Chinese))

11杨刚,张斌.类石墨烯二维原子晶体的微态理论模型.力学学报,2015,47(3)：451-457(YangGang,ZhangBin.Micromorphicmodel of graphene-like two-dimensional atomic crystals.Chinese Journal of Theoretical and Applied Mechanics,2015,47(3)：451-457(in Chinese))

12 Miller RE,Shenoy VB.Size-dependent elastic properties of nanosized structural elements.Nanotechnology,2000,11(3)：139-147

13 Cammarata RC.Surface and interface stress e ff ects in thin films Progress in Surface Science,1994,46(1)：1-38

14 Murdoch AI.The propagation of surface waves in bodies with material boundaries.Journal of the Mechanics and Physics of Solids,1976,24(2)：137-146

15 Gurtin ME,Murdoch AI.A continuum theory of elastic material surfaces.Archive for Rational Mechanics and Analysis,1975,57(4)：291-323

16 Chen WQ,Wu B,Zhang CL,et al.On wave propagation in anisotropic elastic cylinders at nanoscale：surface elasticity and its e ff ect.Acta Mechanica,2014,225(10)：2743-2760

17 Huang GY,Yu SW.E ff ect of surface piezoelectricity on the electromechanical behaviour of a piezoelectric ring.Physica Status Solidi(b),2006,243(4)：R22-R24

18 Yan Z,Jiang LY.Surface e ff ects on the electromechanical coupling and bending behaviours of piezoelectric nanowires.Journal of Physics D:Applied Physics,2011,44(7)：075404

19 Yan Z,Jiang LY.The vibrational and buckling behaviors of piezoelectric nanobeams with surface e ff ects.Nanotechnology,2011,22(24)：245703

20 Yan Z,Jiang LY.Electromechanical response of a curved piezoelectric nanobeam with the consideration of surface e ff ects.Journal of Physics D:Applied Physics,2011,44(36)：365301

21 Zhang CL,Chen WQ,Zhang C.On propagation of anti-plane shear waves in piezoelectric plates with surface e ff ect.Physics Letters A,2012,376(45)：3281-3286

22 Zhang LL,Liu JX,Fang XQ,et al.Size-dependent dispersion characteristics in piezoelectric nanoplates with surface e ff ects.Physica E:Low-dimensional Systems and Nanostructures,2014,57：169-174

23 Chen WQ.Surface e ff ect on Bleustein-Gulyaev wave in a piezoelectric half-space.Theoretical and Applied Mechanics Letters,2011,1(4)：041001

24 BleusteinJL.Anewsurfacewaveinpiezoelectricmaterials.Applied Physics Letters,1968,13(12)：412-413

25 Gulyaev YV.Electroacoustic surface waves in solids.Soviet Physics JETP,1969,9：37-38

26 Stroh AN.Dislocations and cracks in anisotropic elasticity.Philosophical Magazine,1958,3(25)：625-646

27 Stroh AN.Steady state problems in anisotropic elasticity.Journal of Mathematical Physics,1962,41(2)：77-103

28 Lothe J,Barnett DM.Integral formalism for surface waves in piezoelectric crystals. Existence considerations. Journal of Applied Physics,1976,47(5)：1799-1807

29 Barnett DM,Lothe J.Free surface(Rayleigh)waves in anisotropic elastic half-spaces：the surface impedance method.Proceedings of the Royal Society of London A,1985,402(1822)：135-152

30 Lothe J,Barnett D M.Further development of the theory for surface waves in piezoelectric crystals.Physica Norvegica,1977,8(4)：239-254

31 Abbudi M,Barnett DM.On the existence of interfacial(Stoneley)waves in bonded piezoelectric half-spaces.Proceedings of the Royal Society of London A,1990,429(1877)：587-611

32 Tiersten HF.Wave propagation in an infinitpiezoelectric plate.Journal of the Acoustical Society of America,1963,35(2)：234-239

33 Ding HJ,Chen WQ.Three Dimensional Problems of Piezoelasticity.New York：Nova Science Publishers,2001

34 Soh AK,Liu J,Lee KL,et al.Moving dislocations in general anisotropic piezoelectric solids.Physica Status Solidi(b),2005,242(4)：842-853

35 Ding HJ,Liang J.The fundamental solutions for transversely isotropic piezoelectricity and boundary element method.Computers&Structures,1999,71(4)：447-455

36 Sezawa K,Kanai K.Discontinuity in dispersion curves of Rayleighwaves.Bulletin of the Earthquake Research Institute,1935,13：237-244

SURFACE WAVES IN A PIEZOELECTRIC HALF-SPACE WITH SURFACE EFFECT1)

Zhou Weijian Chen Weiqiu2)
(Department of Engineering Mechanics，Zhejiang University，Hangzhou 310027，China)(State Key Lab of Fluid Power and Mechatronic Systems，Zhejiang University，Hangzhou 310027，China)(Key Laboratory of Soft Machines and Smart Devices of Zhejiang Province，Hangzhou 310027，China)

The fast developments in nanotechnology enable the wide applications of piezoelectric nano-structures in nano-electromechanical systems,forming new research directions such as nanopiezotronics.Compared with the traditional macroscopic piezoelectric materials,nano-scaled piezoelectric materials present di ff erent mechanical properties,possibly due to the existence of surface e ff ect,one of the main reasons for explaining the di ff erence.This paper concerns the propagation of surface waves in a generally anisotropic piezoelectric half-space with surface e ff ect.Stroh formalism,Barnett-Lothe integral matrices,and surface impedance matrices are adopted to theoretically derive the dispersion equations of surface waves.For transversely isotropic piezoelectric materials with the isotropic basal plane parallel with the sagittal plane,Rayleigh waves and B-G waves are found to be decoupled from each other,and their dispersion equations are derived in an explicit and compact form.It is rigorously shown that the velocity of Rayleigh waves should be smaller than that of the bulk waves polarized in the depth direction,whilst the velocity of B-G waves should be smaller than thatof the bulk waves polarized in the direction perpendicular to the sagittal plane.In the numerical simulations,PZT-5H is taken as an example to numerically illustrate the influence of surface residual stress and electrical boundary conditions on the dispersion properties of surface waves.It is found that surface residual stress has a significan e ff ect only on the first-orde Rayleigh wave,and the B-G wave under the electric open-circuit condition propagates faster than under the electric closed-circuit condition.The theoretical predictions and numerical results presented in the paper should be helpful in understanding size-dependent dynamic behaviors of piezoelectric structures with surface e ff ect and may provide a solid basis for the design of nano-sized surface acoustic wave devices as well as for the nondestructive testing of nano-sized piezoelectric structures.

surface waves,surface e ff ect,piezoelectric material,Stroh formlism,dispersion relation

O343

：A

10.6052/0459-1879-17-152

2017–05–02 收稿，2017–05–23 录用,2017–05–23 网络版发表.

1)国家自然科学基金资助项目(11532001,11621062).

2)陈伟球，教授，主要研究方向：新型材料的力学，软材料与结构的振动与波动.E-mail：chenwq@zju.edu.cn

周伟建,陈伟球.具有表面效应的压电半空间中的表面波.力学学报,2017,49(3)：597-604

Zhou Weijian,Chen Weiqiu.Surface waves in a piezoelectric half-space with surface e ff ect.Chinese Journal of Theoretical and Applied Mechanics,2017,49(3)：597-604