超临界CO2--水两相流与CO2毛细捕获：微观孔隙模型实验与数值模拟研究1)

胡 冉 陈益峰 万嘉敏 周创兵

∗(武汉大学水资源与水电工程科学国家重点实验室，武汉430072)†(劳伦斯伯克利国家实验室地球能源科学部，美国伯克利94720)

超临界CO2
--水两相流与CO2毛细捕获：微观孔隙模型实验与数值模拟研究1)

胡 冉∗,†陈益峰∗,2)万嘉敏†周创兵∗

∗(武汉大学水资源与水电工程科学国家重点实验室，武汉430072)†(劳伦斯伯克利国家实验室地球能源科学部，美国伯克利94720)

CO2毛细捕获机制是CO2地质封存中的关键科学问题，然而有关孔隙尺度下(微米极)超临界CO2毛细捕获的研究较少.采用高压流体--显微镜--微观模型实验装置，开展超临界CO2条件(8.5MPa,45◦C)下CO2驱替水(排水)和水驱替CO2(吸湿)实验，采用高分辨率照相机采集CO2水两相流运动图像，并借助光学显微镜直接观测孔隙尺度下CO2毛细捕获特征.同时，采用计算流体动力学方法对实验过程进行三维数值模拟.数值模拟不仅反映了实验过程中两相流驱替锋面的推进过程，还刻画了孔隙尺度下被捕获的CO2液滴/团簇三维空间形态特征.最后，基于数值模拟给出了CO2初始饱和度与残余饱和度曲线，即毛细捕获曲线，并对比分析了3种毛细捕获曲线预测模型(即Jurauld模型、Land模型和Spiteri模型)的优劣.分析表明，Jurauld模型的描述能力稍优于Land模型，Spiteri模型的描述能力较弱.由于Land模型只需单个参数，且参数具有明确的物理意义，因此在实际工程中，建议优先采用Land模型.

CO2地质封存,微观模型,两相流,数值模拟,毛细捕获

引言

大量研究表明，化石燃料燃烧产生的CO2超量排放是全球气候变暖的主要原因.目前，CO2地质封存(geological carbon sequestration,GCS)被广泛认为是缓解CO2引起温室效应的有效途径之一.该方法将CO2注入地下以达到长期稳定、安全封存的目的.CO2地质封存场所包括衰竭油气藏、不可开采煤层和地下咸水含水层[1].世界气候变化委员会研究报告指出[2]，全世界范围内CO2在咸水含水层中的封存量可占2005年—2050年总排放量的20%～50%.我国盐水盆地众多，CO2地质封存潜力巨大[34].当CO2注入地下至少800m深的咸水层中，CO2以超临界状态渗入岩石孔隙中，孔隙水被CO2驱替；当CO2停止注入时，地下水回流，原先注入到孔隙中的CO2一部分被水的回流驱替，而残余部分由于毛细力和孔隙结构的双重作用，被捕获在孔隙中.这种捕获机制被称为毛细捕获(capillary trapping或residual trapping)[5].在GCS中，毛细捕获意义尤其重要：一方面，由于毛细捕获主要依靠岩石孔隙间的毛细力捕获CO2，对岩石的完整性要求不高，从而提高了地质封存的安全性[6]；另一方面，CO2以团簇形态位于孔隙中，CO2、水、矿物三者的接触，促进了溶解和化学反应的进行，从而对CO2超长期矿物捕获具有重要影响.

孔隙介质中CO2毛细捕获量(饱和度)受控于CO2水两相流过程，与介质的湿润性[710]、孔隙结构[1012]、CO2注入速率[1314]与初始饱和度等因素密切相关.CO2初始饱和度与残余饱和度的关系称为毛细捕获曲线，该曲线具有重要的工程意义.国内外研究人员对CO2毛细捕获机制开展了大量实验与数值模拟研究.在实验方面，目前的研究手段主要包括：(1)基于CT(computed tomography)扫描的岩芯驱替或玻璃珠驱替实验[1517];(2)基于照相机/显微镜观测的微观模型实验[1820].Al-Raoush[8]研究了介质湿润性对毛细捕获量及其分布的影响，结果表明介质的亲水性愈强，毛细捕获量愈大，被捕获的液滴尺寸愈大.Chaudhary等[10]研究介质湿润性与孔隙孔喉比对CO2毛细捕获的影响，实验结果表明：亲水性愈强，孔喉比愈大，CO2的捕获量愈高.Andrew等[21]针对石灰岩开展了CO2水排驱实验，实验结果表明，被毛细捕获的CO2液滴/团簇，其尺寸呈指数分布特征.武爱兵等[22]通过超临界CO2(sc CO2)排驱饱水砂岩岩芯实验，研究了盐水浓度对CO2毛细量的影响，并指出两相流的排驱形式可分为活塞式、携带式和溶解式.Niu等[17]研究了温度、压力和咸水浓度对砂岩孔隙中CO2残余总量与分布特征的影响.在上述实验研究中，尽管岩芯试样能够较精确反映岩石的三维孔隙结构，然而由于CT扫描精度有限，较难获取微米尺度下CO2毛细捕获的细部特征.

另一方面，基于激光刻蚀技术制备而成的微观孔隙模型，可以采用显微镜和照相机直接观测微米尺度下的两相流动状态，能够采集到比CT扫描更高分辨率的流体运动图像[2325].研究人员基于微观模型实验研究了驱替速率与流体黏滞系数[1820]、介质湿润性[26]和孔隙结构[27]对驱替模式和毛细捕获的影响.Lenormand等[20]和Zhang等[28]研究了两种互不混溶流体驱替过程中的黏性指进、毛细指进与稳定驱替模式，表明驱替模式受控于两个特征参数，即毛细数和黏度比.Cottin等[29]则研究了微观模型湿润性对指流形态的影响，表明当介质由亲水性过渡为中等亲水性时，指流形态向稳定的方向发展.但以上研究较少关注超临界CO2条件下CO2的毛细捕获特征.

除实验研究外，数值模拟也在孔隙尺度下的两相流运动规律与毛细捕获机制研究方面发挥了重要作用.常用的数值模拟方法有孔隙网络模型方法[30]、格子玻尔兹曼方法[31]、光滑粒子流体动力学方法[32]和计算流体动力学方法[3334].其中，前3种方法所需的模型参数较多，且模型参数不独立，因此在计算之前，需要对参数进行标定[35].计算流体动力学方法的优点在于模型参数较少，无需标定，但对计算资源的要求较高.

本文基于高压流体--显微镜--微观模型观测系统，研究超临界CO2条件(8.5MPa、45◦C)下CO2水两相流运动规律以及孔隙尺度下 CO2毛细捕获特征，采用直接求解纳维--斯托克斯方程模拟两相流运动过程，并与实验结果进行对比研究.最后，基于数值模拟得到的CO2初始饱和度与残余饱和度曲线(毛细捕获曲线)，对比分析了3种残余饱和度预测模型的优劣.

1 实验装置与实验流程

1.1 高压--显微镜--微观模型实验装置

采用如图1(a)所示的实验装置开展超临界CO2水驱排实验，该装置主要由微观模型观测子系统、流量控制子系统、温度控制子系统和CO2水反应器子系统四大部分组成.

(1)微观模型观测子系统由微观模型安装平台、照相机(Carl Zeiss,AxioCam MRc5)和倒置的光学显微镜(Carl Zeiss,Observer Z1.m)组成.微观模型长20mm，宽10mm，孔隙喉道宽度为50µm，孔隙深度为 40µm，孔隙总体积 (pore volume)为 1.97µL，如图1(b).微观模型由特定的螺丝安装在平台上.照相机采集微观模型全范围(20mm×10mm)内的流体流动状态图像(1帧/秒)，显微镜采集孔隙尺度(微米级)下的流体流动图像.照相机和显微镜通过数据线与电脑连接，采集的图像实时传入电脑.

(2)流量控制子系统由高精度高压流量泵(Teledyne ISCO,500HP×2和65HP)组成.如图1(a)所示，泵A以恒定流量向微观模型入口注入超临界CO2，泵B以恒定流量注入水，泵C连接微观模型出口，确保流体系统为恒定压力(8.5MPa).

(3)CO2水反应器子系统由搅拌反应器 (Parr,model 4560)、泵A和CO2气缸组成.尽管水和CO2是两种互不混溶流体，但在微观孔隙模型中，由于孔隙体积极小(1.97µL)，无论是少量CO2溶解于水(形成不稳定的H2CO3)，还是微量水溶解于CO2，都会对两相流运动特性产生显著影响[24].为了消除溶解对两相流的影响，在泵A恒压(8.5MPa)条件下，搅拌棒匀速转动，确保搅拌器上层CO2与下层水充分反应，以达到两相平衡(充分饱和).

(4)温度控制子系统由隔热室、温度传感控制器和加热灯组成.(1)、(2)和(3)三个子系统位于密闭的隔热室中，室内由加热灯提供热量，室内的温度传感器(Omega,Type T)与室外的温度控制器(Cole Parmer,EW-89000-10)相连，以确保隔热室内的温度保持在 (45±1)◦C.

图1 高压流体--显微镜--微观模型实验装置Fig.1 High-pressure fluids-microsco y-micromodel system

1.2 实验流程

实验过程包括CO2、水两种流体的制备、微观模型清洗、CO2与水驱排、CO2与水两相流平衡4个阶段.试验重复3次，具体过程如下：

(1)CO2与水两相流体制备.在本研究中，不考虑CO2与水的相互溶解，因此实验中的CO2和水须达到相平衡状态.为反映地层咸水浓度，采用脱离子水和高纯度NaCl(Sigma-Aldrich,ACS reagent grade)配置0.01mol/L的NaCl溶液.将该溶液注入搅拌器，并将CO2由气缸注入泵A.泵A与搅拌器连接，将流体压力和温度分别提至8.5MPa和45◦C.搅拌棒匀速转动24h，确保CO2与水两者充分饱和.

(2)微观模型清洗.采用脱离子水以500µL/min的流量清洗微观模型，持续10min，然后放置在烘箱内在120◦C条件下烘24h.

(3)CO2与水驱排.常压下，采用泵C向微观模型注入脱离子水，确保微观模型达到饱水状态，然后将压力提升至8.5MPa.打开泵C与微观模型管路，将制备好的水(0.01mol/L NaCl)以200µL/min流量注入微观模型，持续5min.然后，打开泵A与微观模型管路，CO2与水在注入口A处相接触.此后将实验静置3h，以确保CO2与水达到热平衡状态.3h后，泵A以192µL/min的流量向微观模型中注入超临界CO2以驱替水，该过程为排水过程(drainage).照相机以1帧/秒的速率采集图像.由于微观模型孔隙体积较小 (1.97µL)，该排水过程仅持续 2s便可达到稳定状态.排水结束后，关闭泵A与微观模型管路，打开泵B与微观模型管路，以同样的流量(192µL/min)注入水，即吸湿过程(imbibition).该过程仅持续3s便可达到稳定状态

(4)CO2与水两相流平衡.驱排过程结束后，关闭微观模型入口与出口阀门.根据照相机采集的图像，5min后微观模型内流体便可达到平衡状态.此时，采用显微镜采集微观模型中被毛细捕获的CO2液滴/团簇的形态与分布.

本实验装置是基于文献[23]改进而成的，有关实验细节，可参考文献[23].

2 数值模拟

2.1 控制方程

微观模型中，CO2与水两相驱替物理过程可由纳维--斯托克斯方程描述，即流体动量守恒方程

与质量守恒方程

式中,u为流体速度,p为流体压力，µ为流体黏滞系数，fs表征了由CO2与水界面引起的毛细力对流体动量的贡献.fs可表达为

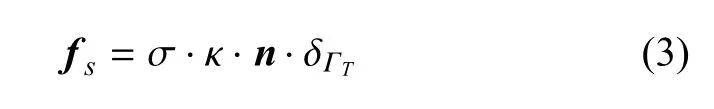
式中,σ为界面张力,κ为曲率,n为界面指向湿润相(水相)的单位法向量，δΓT为Dirac delta函数，界面处为1，其他处为0.

式(1)涉及到两相流运动，在各相内部，式(1)可分别描述各个相的流体运动.对于两相流体界面，目前广泛采用流体体积法(volume of flui，VOF)刻画界面的演化[35].定义无量纲变量，即流体体积分数α，来表征两相界面的空间位置(如图2所示)

图2 流体体积法示意图Fig.2 Illustration of the volume of flui method

在流体体积方法中，体积分数的演化可由如下方程描述

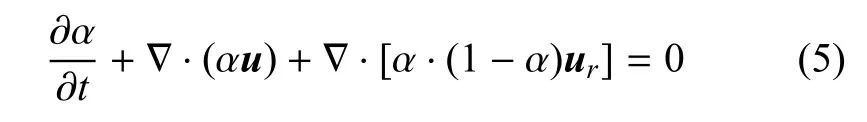
式中，ur为人为构造的流速，以提升界面处的数值稳定性与鲁棒性[36].

根据式(4)，式(1)中的流体黏度与密度可表达为流体体积分数的函数

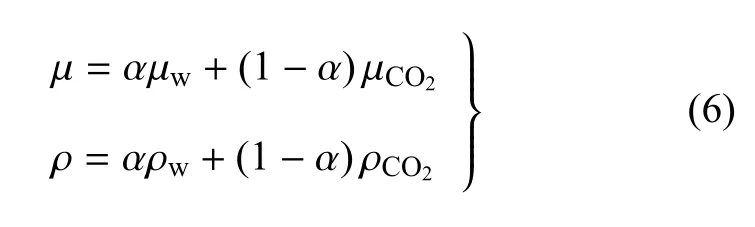
式中，µw和µCO2分别为水和CO2的黏滞系数，ρw和ρCO2分别为水和CO2的密度.

考虑到界面法向量 n=∇α，界面曲率κ=∇·(∇α/‖∇α‖).将 n,κ与α的关系式与式(3)代入式(1)，并联立式(2)和式(5)，可得到CO2水两相流运动的控制方程

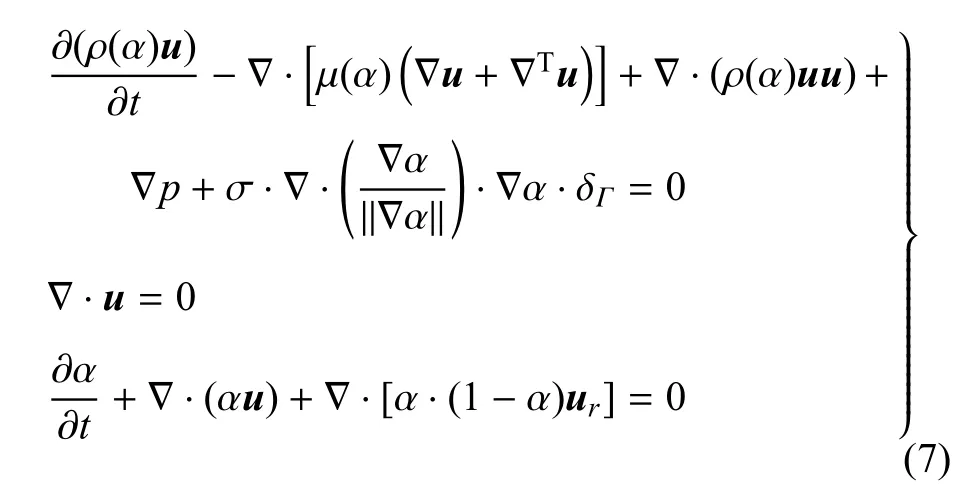
2.2 模拟方法

OpenFOAM[36]是一个得到国内外广泛应用的计算流体动力学开源软件包，其开源特性使研究人员可根据问题求解的需要更改底层代码.本文在Open-FOAM平台上采用有限体积法对式(7)进行了数值实现.微观模型的计算网格如图3所示，共剖分六面体单元1962924个，节点2712905个，单元的尺寸控制在6～9µm.流体参数如表1所示.

图3 微观模型有限体积网格Fig.3 Finite volume mesh for the micromodel

表1 超临界CO2与水两相流参数Table 1 The parameters for the supercritical CO2-water two-phase flui fl w

需要指出的是，本文微观模型壁面为亲水性.在8.5MPa和45◦C的高温高压条件下，基于不同区域的显微镜照片，测量了10组CO2与水在微观孔隙模型壁面上的接触角，平均值为22◦.在OpenFOAM中，接触角对两相流界面的影响由下式表征[35]

式中,θ为壁面接触角，ns和nt分别为壁面的单位法向量和切向量.

根据实验条件，数值模拟的初始条件为：在模型区域内，u=0，α=1，p=8.5MPa.边界条件为：(1)在排水阶段(drainage)，在注入口A，u=0.32m/s(根据流量折算)，∇p=0，α =0；在出口，∂u/∂x=∂u/∂y= ∂u/∂z=0，p=8.5MPa，∇α =0，(2)在吸湿阶段(imbibition)，在注入口B，u=0.32m/s(根据流量折算)，∇p=0，α =1；在出口，∂u/∂x= ∂u/∂y=∂u/∂z=0，p=8.5MPa，∇α =0，(3)在平衡阶段(注入口与出口阀门关闭)，在注入口B和出口，u=0m/s，p=8.5MPa，∇α =0.

数值模拟采用并行计算，以确保在可接受的时间内获得解答.基于国家天河II号超级计算机，采用96个CPU核心并行模拟CO2水排水、吸湿与平衡过程，共耗机时23040核·小时.对于3.3节毛细捕获曲线的数值模拟，采用768个CPU核心进行数值模拟，共耗机时115200核·小时.

3 结果分析

如1.2节所述，对实验过程重复3次，获得3组实验图像.对于CO2的分布特征与CO2液滴/团簇形态，采用第1组实验图像与数值模拟进行对比分析；对于CO2的饱和度，采用3组实验数据的平均值与数值模拟结果进行对比.采用ImageJ软件[39]对实验图形进行后处理，提取CO2饱和度的量值.

3.1 超临界CO2水驱排实验与数值模拟对比

图4给出了两相不混溶流体驱替过程中呈现出的3种流动特征，即黏性指进、毛细指进与稳定流.这3种流动特征受控于两个特征参数，即毛细数(Ca)和黏度比(M).毛细数反映了两相流所受到的黏滞力与毛细力之比的量值.Ca和M的定义如下

式中,ui和µi分别为驱替流体的特征流速与黏滞系数，µ2为被驱替流体的黏滞系数.由于实验条件不一致，Lenormand等(虚线)[20]和Zhang等(实线)[28]给出的结果有一定差异，如图4所示.

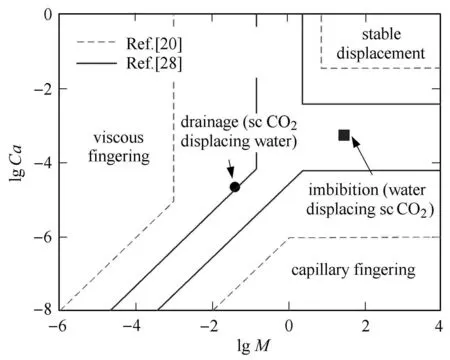
图4 两种互不相容流体流动状态相图Fig.4 The phase diagram for displacement pattern within the two-phase immiscible flui fl w

将表1所示参数代入式(8)和式(9)可得：在排水阶段(drainage，CO2驱替水)，毛细数与黏度比分别为，Ca=2.24×10-5，M=0.038；在吸湿阶段(imbibition，水驱替CO2)，Ca=5.87×10-4，M=26.24.由图4可知，在本实验的排水阶段(drainage)，两相流驱替过程既有毛细指进也有黏性指进.

图5给出了排水0.1s时，微观模型中CO2分布的数值模拟结果.由于CO2注入口位于左上方，而恒定压力出口位于右下方，因此CO2指进向右下方倾斜.由图可知，CO2驱替水过程呈现强烈的指进现象.根据指进的宽度与长度，可初步判定：在左上方，CO2锋面推进为毛细指进，而在左下方，CO2锋面前移为黏性指进.图5所示的局部放大图给出了CO2驱替锋面处，CO2与水界面的三维形态.对于本文研究的亲水性介质而言，界面向湿润相(水相)凸起.

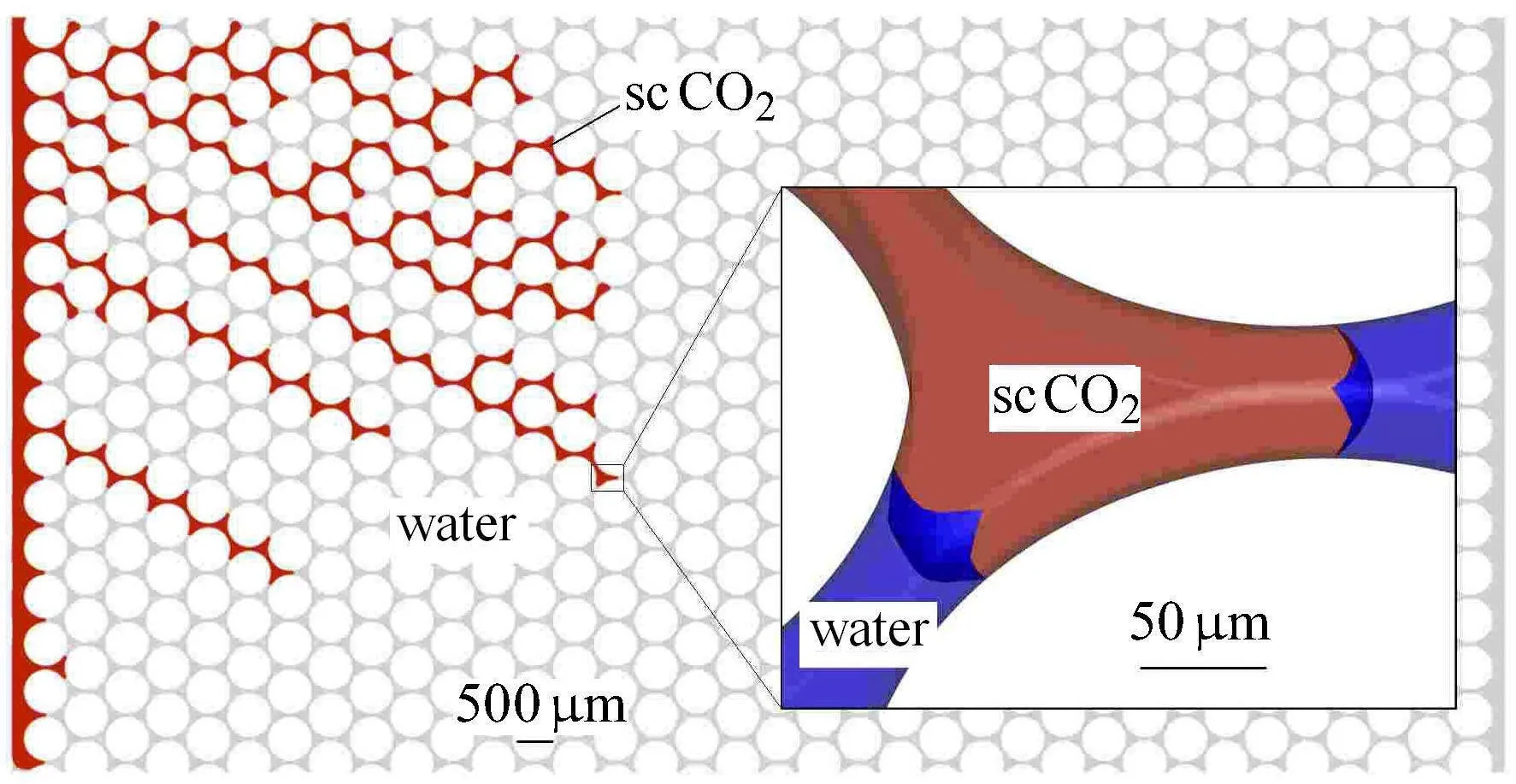
图5 排水过程(drainage)0.1 s时刻数值模拟结果Fig.5 The numerical results for the two-phase flui fl w after 0.1 s of drainage

图6给出了排水1s时，CO2分布的实验观测与数值模拟对比结果.由图可知，在排水1 s时刻，驱替相 (CO2)已到达出口处，驱替穿透.考虑到排水实验注入口与出口的位置，在微观模型左下方与右上方局部区域，CO2的局部饱和度较小.图6(a)的CO2饱和度为51.1%，三组实验的CO2饱和度平均值为(51.0±3.9)%.CO2饱和度的数值模拟结果为53.9%(图6(b)).排水结束后，CO2饱和度的实验结果为(58.3±2.1)%，数值模拟结果为61.3%，两者基本一致.

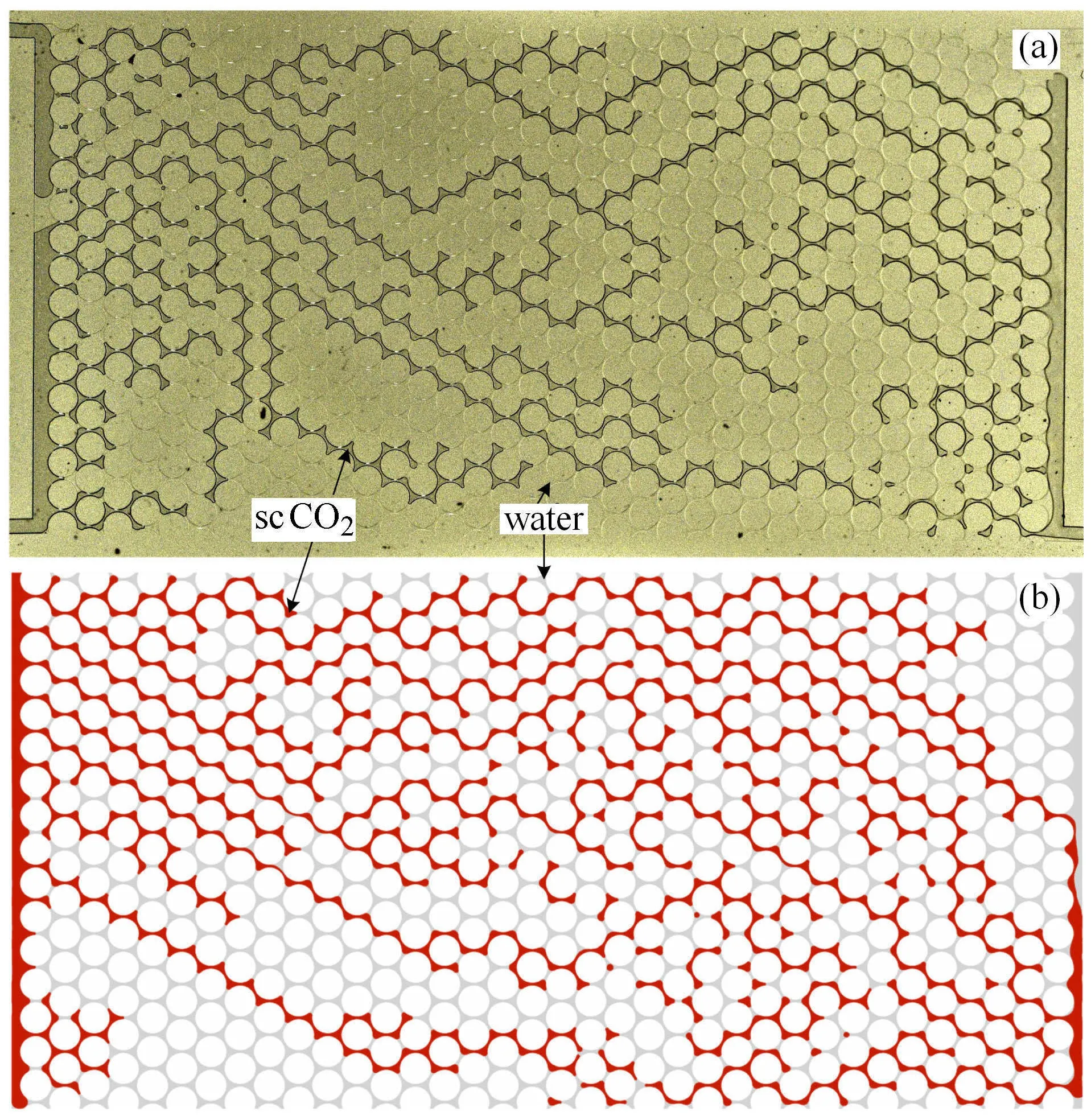
图6 排水过程(drainage)1 s时刻实验(由照相机采集)与数值模拟对比((a)实验结果,(b)数值模拟结果)Fig.6 Comparison between numerical results and the DSLR captured images after 1 s of drainage((a)experimental result,(b)numerical simulation)

排水过程持续2s后，水从微观模型左下方以恒定流量注入，以驱替排水过程中注入的CO2.图7给出了吸湿0.1s时，CO2相分布特征的数值模拟结果.由图可知，在水相注入口附近，CO2局部饱和度趋于零，表明在此区域，水以“活塞式”方式驱替CO2.图7中的局部放大图表明，在吸湿过程中，部分CO2以液滴形式存在于孔隙中.

吸湿1s时，CO2分布的实验观测与数值模拟对比结果如图8所示.由图可知，在吸湿1s时刻，实验观测结果表明CO2以液滴/团簇形式存在于单个或多个孔隙中.CO2局部饱和度在微观模型左端和右端较高，而在中间偏左侧较低.数值结果表明,在微观模型左侧 (水相注入口附近区域)，水以 “活塞式”驱替CO2，导致CO2的局部饱和度趋于零.而在此区域，实验观测的CO2饱和度较大.其原因是在排水阶段(drainage)，有一定体积的超临界CO2进入左下方入口处(图8(a)).当吸湿开始时(imbibition)，在排水阶段进入的超临界CO2被水从入口区域驱替至微观孔隙中，从而导致左下方附近区域的CO2饱和度过大.由此可见，对于本文采用的微观流体模型，由于流体入口段不均匀，使得微观孔隙模型中的左边界不能成为均匀的过流断面，从而在一定程度上影响入口端附近流场的分布规律以及CO2或水的局部饱和度.

图7 吸湿过程(imbibition)0.1s时刻数值模拟结果Fig.7 The numerical results for the two-phase flui fl w after 0.1s of imbibition

图 8(a)的 CO2饱和度为 29.4%，三次重复实验的平均值为(27.7±2.3)%，数值模拟结果为21.9%(图8(b)).由此可见，在吸湿1s时刻，数值模拟与实验结果有一定差异.造成偏差的原因如下：(1)如前所述，在排水阶段进入入口段的CO2，在吸湿初期(imbibition)被水驱替至微观孔隙中，导致CO2饱和度的实验值偏大；(2)由于制造工艺，微观模型表面有微小的(约0.5µm)起伏度(粗糙度)，而在数值模拟中，几何模型没有反映这种起伏度.考虑到微观模型喉道尺寸为50µm，深度为40µm，在吸湿阶段，毛细数增大，黏滞力对流体运动的影响增大.因此，起伏度对流体运动的影响在吸湿阶段被放大，从而导致数值模拟与实验结果的偏差增大；(3)在本文数值模拟中，接触角取常数，而忽略了动态接触角的影响.当毛细数大于10-4时，流体与孔隙壁面的前沿和后沿接触角具有一定差异，接触角的这种动态效应对流体界面的推进具有一定影响[4041].

图8 吸湿过程(imbibition)1s时刻实验(由照相机采集)与数值模拟对比((a)实验结果,(b)数值模拟结果)Fig.8 Comparison between numerical results and the DSLR captured images after 1s of imbibition((a)experimental result,(b)numerical simulation)

3.2 CO2毛细捕获特征的实验与数值模拟对比

水驱替CO2持续3s后，吸湿过程结束.关闭微观模型注入口与出口.由于此刻注入口与出口端的压力差为零，微观模型中的流体流速将逐渐递减至零，流体压力将变为恒定压力值(8.5MPa).由照相机与显微镜采集的图像可知，阀门关闭5min后，两相流达到平衡状态.图9给出了平衡状态下被捕获的CO2液滴/团簇形态与位置.由图可知，在本文研究的亲水性介质中，被捕获的 CO2以液滴或团簇的形式存在于孔隙中，CO2液滴或团簇呈球状(或近似球状)，该实验观测结果与以往的实验结果一致[8,10].这些液滴或团簇位于单个孔隙(pore body)中(图9(d),图9(f)和图9(g))，或位于两个相邻的孔隙中(图9(e))，相邻的孔隙由孔喉连接.数值模拟结果较好地反映了被捕获CO2液滴/团簇的这种分布特征.CO2毛细捕获的数值模拟结果如图9(h)～图9(n)所示.被捕获的CO2液滴/团簇部分位于单个孔隙中(图9(h)、图9(j)和图9(k))，部分位于两个相邻的孔隙中(图9(i)).由图9(h)～图9(k)的三维视图可知，对于亲水性介质，CO2液滴的三维形态为凸状体，这与基于CT扫描的实验观测结果一致[8].

如图 9(b)所示，CO2残余饱和度为 10.3%，三组实验的平均值为 (9.2±1.1)%，数值模拟结果为7.9%(图9(m)).由于CO2残余饱和度与驱替流速(或毛细数)密切相关，研究表明[4243]，当毛细数大于1×10-6时，一般服从Snwr～λlg(Ca)的规律，其中λ为常数.毛细数越小，两种流体的毛细力对两相流运动的影响越显著.本实验中，在吸湿阶段(imbibition)，毛细数为Ca=5.87×10-4，M ＞1，毛细力对两相流的影响不显著，驱替模式属于毛细指进和稳定驱替的过渡区(图4).

图9 超临界CO2毛细捕获实验结果(a)～(g)与数值模拟结果(h)～(n).(a)和(c)为显微镜低倍物镜采集的被捕获CO2液滴/团簇分布；(b)为照相机采集的被捕获CO2液滴/团簇整体分布；(d)～(g)为显微镜高倍物镜采集的单个孔隙中被捕获CO2团簇分布形态.(m)为被捕获的CO2液滴/团簇整体分布；(l)和(n)为被捕获的CO2团簇在多个孔隙内的分布；(h)～(k)为被捕获的CO2团簇在单个孔隙中的形态Fig.9 The observed(a)～ (g)and simulated(h)～ (n)shape and distribution of trapped CO2droplets/clusters：(a)and(c)the distribution of trapped CO2droplets/clusters at multiple pores;(b)the distribution of trapped CO2droplets/clusters at the full scale of micromodel;(d)～(g)the distribution of trapped CO2droplets/clusters at a single pore.(m)the distribution of trapped CO2droplet/cluster at the full scale of micromodel;(l)and(n)the distribution of trapped CO2droplets/clusters at multiple pores;(h)～(k)the distribution of trapped CO2droplets/clusters at a single pore

受微观孔隙模型实验周期的限制，在本实验中，驱替流速设定为192µL/min，没有采取相对较小的驱替流速.此外，微观模型可承受最大值为10MPa的内外压力差.在以往的微观孔隙模型实验研究中[24,44]，一般将微观模型置入透明压力盒中.微观孔隙模型内部加压时，压力盒(微观孔隙外部)也同时加压，以确保微观孔隙内外压差不太大.本研究未采用压力盒，因而实验装置简单，无需染色剂便可直接观测微观模型中的两相流运动[23].然而，由于没有压力盒抵消压差，在内外8.5MPa的压差条件下，若实验持续较长时间(6h)，微观孔隙模型存在“爆裂”的危险.由于小流量驱替实验将显著延长实验的持续时间，因此为了减低实验风险，本研究采用较大的驱替流速，以保证在相对较短的时间内获得两相驱替的全过程与毛细捕获的实验结果.在以后的研究中，将改进实验装置，在保证实验安全可靠的前提下，采用更小的驱替流速，研究两相流的运动规律.

3.3 毛细捕获曲线实验/模拟结果与预测模型对比

在CO2地质封存和石油开采中，孔隙介质的非湿润相初始饱和度(Snwi)与残余饱和度(Snwr)曲线对于工程应用尤其重要，该曲线称为毛细捕获曲线.Land[45]提出了单参数预测模型，描述两者之间的关系.Land模型表达如下

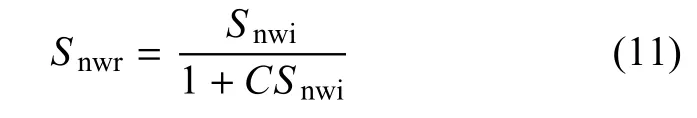
式中,Snwi和Snwr分别为初始饱和度和残余饱和度，C为Land模型参数.Snwi为排水过程结束或吸湿过程开始时，介质的非湿润相饱和度.Land模型参数可通过介质的最大饱和度和最大的残余饱和度计算得到

式中,Snwr,max和Snw,max分别为介质非湿润相最大残余饱和度和最大饱和度.

Jerauld[46]在Land模型的基础上，提出了两参数模型，以反映介质湿润性的非均质性对介质残余饱和度的影响，表达如下

式中,b为模型参数.对比式(11)与式(13)可知，当b=0时，Jerauld模型直接退化为Land模型.

Spiteri等[47]提出了能够反映不同湿润性对介质残余饱和度影响的预测模型

式中,α和β为模型参数.

对于上述3种残余饱和度预测模型，采用数值模拟与实验结果进行对比研究.在本文实验中，当排水过程结束时，CO2分布不再改变，因此可认为CO2达到了初始饱和度的最大值.由于本文开展的排水、吸湿实验在5s内便分别达到稳定状态，较难获得初始饱和度和残余饱和度的其他量值.为获取本文微观模型不同的Snwi与Snwr量值，采用数值方法模拟不同持续时间(小于2s)的排水过程，得到初始饱和度，继而模拟吸湿过程，得到对应的残余饱和度.

图10给出了微观模型初始饱和度与残余饱和度的实验、数值模拟与预测模型拟合结果.表2列出了基于数值模拟结果，各个模型的最优拟合参数与均方偏差.由表2可知，Jerauld模型与Land模型与数值模拟结果的均方偏差分别为0.0066和0.01，两者相差不大，而Spiteri模型的均方偏差为0.0190.因此，Jerauld模型与Land模型与数值模拟结果吻合较好，但Jerauld模型优于Land模型，Spiteri模型的描述能力最差.

表2 各模型的最优拟合系数与均方偏差Table 2 The fittin parameters and the root-mean-square-error(RMSE)for the three models

图10 超临界CO2毛细捕获曲线数值模拟结果与不同模型对比Fig.10 The comparison of the capillary trapping curve between the numerical simulation/experimental data and three di ff erent models

由图10可知，当初始饱和度小于7%时，毛细捕获曲线与1：1直线重合，表明当注入CO2的体积分数小于0.07时，全部CO2都被捕获于介质中.在此阶段，Jerauld模型吻合效果明显优于Land模型与Spiteri模型.而当初始饱和度大于30%时，残余饱和度基本保持不变.Jerauld模型与Land模型都能反映这种趋势，而Spiteri模型曲线在初始饱和度大于45%后，开始下降.图10也给出了初始饱和度与残余饱和度的实验结果及其误差图.对于实验结果：Snwi=(58.3±2.1)%，Snwr=(9.2±1.1)%；对于数值模拟：Snwi=61.3%，Snwr=7.9%，表明无论是初始饱和度还是残余饱和度，数值模拟结果均小于实验结果.数值模拟与实验结果的偏差主要受3.1节所述的3个方面原因的影响.Raeini等[33]针对LV60砂岩开展了CO2毛细捕获的实验与数值模拟对比研究，表明在初始饱和度大于0.5的区域，CO2毛细捕获的数值模拟结果与实验结果的绝对偏差为2%～4%.在本文对比研究中，实验与模拟的绝对偏差为1.3%.

4 结论

本文采用高压流体--显微镜--微观模型实验装置，开展了超临界CO2条件下CO2水驱排实验，研究了孔隙尺度下CO2毛细捕获特征，同时基于开源软件包OpenFOAM对CO2水两相流实验过程进行了数值模拟，最后基于数值模拟与实验结果对比分析了3种毛细捕获模型的优劣.主要结论如下：

(1)超临界CO2驱替水呈现出强烈的指进现象，这种指进既包含黏性指进，也包含毛细指进.数值模拟结果较好地反映了这种指进现象，同时也很好地刻画了指进锋面的三维形态.

(2)对于本文研究的亲水性介质，在实验观测中，被捕获 CO2液滴/团簇位于单个或者多个孔隙中.数值模拟不仅反映了这一特征，还刻画了CO2液滴/团簇的三维空间形态.

(3)本文对比分析了3种毛细捕获曲线预测模型的描述能力.结果表明：尽管Jerauld模型描述能力最强，但比Land模型多一个参数，且Land模型参数物理意义明确.因此，在实际工程中，建议优先采用Land模型.

本文针对CO2地质封存中毛细捕获机制的微观实验和数值模拟研究具有重要意义.然而，由于驱替流速较大，本文的实验与数值模拟结果只能反映场地CO2注入井附近的超临界CO2毛细捕获特征.此外，在实际GCS工程中，介质湿润性与孔隙结构对CO2毛细捕获具有决定性影响.今后将改进现有实验平台，开展极小驱替流速下的实验研究.

1 Zhang W,Li Y,Xu T,et al.Long-term variations of CO2trapped in di ff erent mechanisms in deep saline formations：a case study of the Songliao Basin,China.International Journal of Greenhouse Gas Control,2009,3(2)：161-180

2 Metz B,Davidson O,De Coninck H,et al.IPCC special report on carbon dioxide capture and storage.Prepared by Working Group III of the Intergovernmental Panel on Climate Change.IPCC,Cambridge,United Kingdom and New York,USA：Cambridge University Press,2005

3李小春,刘延锋,白冰等.中国深部咸水含水层CO2储存优先区域选择.岩石力学与工程学报,2006,25(5)：963-968(Li Xiaochun,Liu Yanfeng,Bai Bing,et al.Ranking and screening of CO2Saline aquifer storage zones in China.Chinese Journal of Rock Mechanics and Engineering,2006,25(5)：963-968(in Chinese))

4李小春,方志明,魏宁等.我国CO2捕集与封存的技术路线探讨.岩土力学,2009,30(9)：2674-2678(Li Xiaochun,Fang Zhiming,Wei Ning,et al.Discussion on technical roadmap of CO2capture and storage in China.Rock and Soil Mechanics,2009,30(9)：2674-2678(in Chinese))

5 Suekane T,Nobuso T,Hirai S,et al.Geological storage of carbon dioxide by residual gas and solubility trapping.International Journal of Greenhouse Gas Control,2008,2(1)：58-64

6 Al Mansoori SK,Itsekiri E,Iglauer S,et al.Measurements of nonwetting phase trapping applied to carbon dioxide storage.International Journal of Greenhouse Gas Control,2010,4(2)：283-288

7 Tanino Y,Blunt M.Laboratory investigation of capillary trapping under mixed-wet conditions. Water Resources Research,2013,49(7)：4311-4319

8 Al-Raoush RI.Impact of wettability on pore-scale characteristics of residual nonaqueous phase liquids.Environmental Science&Technology,2009,43(14)：4796-4801

9 Iglauer S,Pentland C,Busch A.CO2wettability of seal and reservoir rocks and the implications for carbon geo-sequestration.Water Resources Research,2015,51(11)：729-774

10 Chaudhary K,Bayani Cardenas M,Wolfe WW,et al.Pore-scale trapping of supercritical CO2and the role of grain wettability and shape.Geophysical Research Letters,2013,40(15)：3878-3882

11 Tanino Y,Blunt MJ.Capillary trapping in sandstones and carbonates：Dependence on pore structure.Water Resources Research,2012,48(8)：W08525

12 Moura M,Fiorentino EA,Måløy K,et al.Impact of sample geometry on the measurement of pressure-saturation curves：Experiments and simulations.Water Resources Research,2015,51(12)：8900-8926

13 Kimbrel EH,Herring AL,Armstrong RT,et al.Experimental characterization of nonwetting phase trapping and implications for geologic CO2sequestration.International Journal of Greenhouse Gas Control,2015,42：1-15

14 Chatzis I,Kuntamukkula M,Morrow N.E ff ect of capillary number on the microstructure of residual oil in strongly water-wet sandstones.SPE Reservoir Engineering,1988,3(3)：902-912

15 El-Maghraby RM,Blunt MJ.Residual CO2trapping in Indiana limestone.Environmental Science&Technology,2012,47(1)：227-233

16 Andrew M,Bijeljic B,Blunt MJ.Pore-scale imaging of trapped supercritical carbon dioxide in sandstones and carbonates.International Journal of Greenhouse Gas Control,2014,22：1-14

17 Niu B,Al-Menhali A,Krevor SC.The impact of reservoir conditions on the residual trapping of carbon dioxide in Berea sandstone.Water Resources Research,2015,51(4)：2009-2029

18 Zhang C,Oostrom M,Grate JW,et al.Liquid CO2displacement of water in a dual-permeability pore network micromodel.Environmental Science&Technology,2011,45(17)：7581-7588

19 Wang Y,Zhang C,Wei N,et al.Experimental study of crossover from capillary to viscous fingerin for supercritical CO2–water displacement in a homogeneous pore network.Environmental Science&Technology,2012,47(1)：212-218

20 Lenormand R,Touboul E,Zarcone C.Numerical models and experiments on immiscible displacements in porous media.Journal Of Fluid Mechanics,1988,189：165-187

21 Andrew M,Bijeljic B,Blunt MJ.Pore-scale imaging of geological carbon dioxide storage under in situ conditions.Geophysical Research Letters,2013,40(15)：3915-3918

22武爱兵,李铱,常春等.不同成分盐水驱CO2.现代地质,2014,28(5)：1061-1067(Wu Aibing,Li Yi,Chang Chun,et al.The residual gas saturation of di ff erent components of saline floodin CO2.Geoscience,2014,28(5)：1061-1067(in Chinese))

23 Kim Y,Wan J,Kneafsey TJ,et al.Dewetting of silica surfaces upon reactions with supercritical CO2and brine：pore-scale studies in micromodels.Environmental Science&Technology,2012,46(8)：4228-4235

24 Chang C,Zhou Q,Kneafsey TJ,et al.Pore-scale supercritical CO2dissolution and mass transfer under imbibition conditions.Advancesin Water Resources,2016,92：142-158

25 Chang C,Zhou Q,Oostrom M,et al.Pore-scale supercritical CO2dissolution and mass transfer under drainage conditions.Advances in Water Resources,2017,100：14-25

26 Zhao B,MacMinn CW,Juanes R.Wettability control on multiphase fl w in patterned microfluidics Proceedings of the National Academy of Sciences,2016,113(37)：10251-10256

27 Xu W,Ok JT,Xiao F,et al.E ff ect of pore geometry and interfacial tension on water-oil displacement efficiency in oil-wet microfluidi porous media analogs.Physics of Fluids,2014,26(10)：093102

28 Zhang C,Oostrom M,Wietsma TW,et al.Influenc of viscous and capillary forces on immiscible flui displacement：Pore-scale experimental study in a water-wet micromodel demonstrating viscous and capillary fingering Energy&Fuels,2011,25(8)：3493-3505

29 Cottin C,Bodiguel H,Colin A.Influenc of wetting conditions on drainage in porous media：A microfluidi study.Physical Review E,2011,84(2)：026311

30 Raeesi B,Piri M.The e ff ects of wettability and trapping on relationships between interfacial area,capillary pressure and saturation in porous media：A pore-scale network modeling approach.Journal of Hydrology,2009,376(3)：337-352

31 Liu H,Ju Y,Wang N,et al.Lattice Boltzmann modeling of contact angle and its hysteresis in two-phase fl w with large viscosity di ff erence.Physical Review E,2015,92(3)：033306

32 Bandara U,Tartakovsky AM,Oostrom M,et al.Smoothed particle hydrodynamics pore-scale simulations of unstable immiscible fl w in porous media.Advances in Water Resources,2013,62：356-369

33 Raeini AQ,Bijeljic B,Blunt MJ.Modelling capillary trapping usingfinite-olumesimulationoftwo-phasefl wdirectlyonmicro-CT images.Advances in Water Resources,2015,83：102-110

34 Ferrari A,Jimenez-Martinez J,Borgne TL,et al.Challenges in modeling unstable two-phase fl w experiments in porous micromodels.Water Resources Research,2015,51(3)：1381-1400

35 Ferrari A,Lunati I.Direct numerical simulations of interface dynamics to link capillary pressure and total surface energy.Advances in Water Resources,2013,57：19-31

36 Greenshields C.OpenFOAM User Guide.Version 2.4.0.Open-FOAM Foundation Ltd,2015

37 Batzle M,Wang Z.Seismic properties of pore fluids Geophysics,1992,57(11)：1396-408

38 Wang S,Tokunaga TK.Capillary pressure-saturation relations for supercritical CO2and brine in limestone/dolomite sands：Implications for geologic carbon sequestration in carbonate reservoirs.Environmental Science&Technology,2015,49(13)：7208-7217

39 Abr`amo ffMD,Magalh˜aes PJ,Ram SJ.Image processing with Image J.Biophotonics International,2004,11(8)：36-42

40 Roman S,Soulaine C,AlSaud MA,et al.Particle velocimetry analysis of immiscible two-phase fl w in micromodels.Advances in Water Resources,2015,95：199-211

41 Horgue P,Augier F,Duru P,et al.Experimental and numerical study of two-phase fl ws in arrays of cylinders.Chemical Engineering Science,2013,102(15)：335-345

42 Geistlinger H,Ataei-Dadavi I,Mohammadian S,et al.The impact of pore structure and surface roughness on capillary trapping for 2-D and 3-D porous media：Comparison with percolation theory.Water Resources Research,2015,51(11)：9094-9111

43 Mohammadian S,Geistlinger H,Vogel HJ.Quantificatio of gasphase trapping within the capillary fringe using computed microtomography.Vadose Zone Journal,2015,14(5)：

44 Jimenez-Mart´ınez J,Porter ML,Hyman JD,et al.Mixing in a threephase system：Enhanced production of oil-wet reservoirs by CO2injection.Geophysical Research Letter,2016,43(1)：196-205

45 Land CS.Calculation of imbibition relative permeability for twoand three-phase fl w from rock properties.Society of Petroleum Engineers Journal,1968,8(2)：149-156

46 JerauldG.Generalthree-phaserelativepermeabilitymodelforPrudhoe Bay.SPE Reservoir Engineering,1997,12(04)：255-263

47 Spiteri EJ,Juanes R,Blunt MJ,et al.A new model of trapping and relative permeability hysteresis for all wettability characteristics.SPE Journal,2008,13(3)：277-288

SUPERCRITICAL CO2WATER DISPLACEMENTS AND CO2CAPILLARY TRAPPING:MICROMODEL EXPERIMENT AND NUMERICAL SIMULATION1)

Hu Ran∗,†Chen Yifeng∗,2)Wan Jiamin†Zhou Chuangbing∗∗(State Key Laboratory of Water Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China)†(Lawrence Berkeley National Laboratory，Energy Geosciences Division，Berkeley CA 94720，USA)

The CO2capillary trapping is an important scientifi issue in geological carbon sequestration,but few researches focus on the trapping mechanism at pore scale under supercritical CO2condition.In this study,based on the high-pressure fluids-microsco y-micromodel experimental system,we performed drainage experiment,i.e.supercritical CO2displacing water,and imbibition experiment,i.e.water displacing CO2,under the conditions of 45◦C and 8.5MPa.The DSLR camera was used to capture pictures of CO2-water two-phase immiscible fl w and the microscopy was used to capture the capillary trapping behavior for the supercritical CO2at the pore scale.The computational flui dynamic method was adopted to simulate the two-phase flui fl w processes.The numerical results are generally in agree-ment with the experimental observations,and further provide three-dimensional geometries on the interface during the drainage-imbibition processes and the trapped supercritical CO2droplet/cluster.Finally,the capillary trapping curve,i.e.the relationship between the initial CO2saturation and the residual saturation,was obtained from the numerical results,and we made an assessment of the three capillary trapping models,i.e.Land’s,Jurauld’s and Spiteri’s trapping models.A comparison of the models performance indicates that Jurauld’s model behaves slightly better than Land’s model,whereas Spiteri’s model behaves poorly.However,given that Land’s model only contains one parameter of clear physical meaning,it is recommended for practical use.

geological carbon sequestration,micromodel,two-phase fl w,numerical simulation,capillary trapping

O363.2,V211.1+7

：A

10.6052/0459-1879-16-237

2016–08–26 收稿，2017–02–14 录用,2017–02–15 网络版发表.

1)国家自然科学基金(51409198,51579188)及中国博士后科学基金(2015T80833)资助项目.

2)陈益峰,教授,主要研究方向：岩土介质多场耦合与渗流控制理论.E-mail：csyfchen@whu.edu.cn

胡冉,陈益峰,万嘉敏,周创兵.超临界CO2--水两相流与CO2毛细捕获：微观孔隙模型实验与数值模拟研究.力学学报,2017,

49(3)：638-648

Hu Ran,Chen Yifeng,Wan Jiamin,Zhou Chuangbing.Supercritical CO2water displacements and CO2capillary trapping：micromodel experiment and numerical simulation.Chinese Journal of Theoretical and Applied Mechanics,2017,49(3)：638-648