超弹性镍钛形状记忆合金单轴相变棘轮行为的宏观唯象本构模型1)

周 廷 阚前华 康国政 邱 博

(西南交通大学力学与工程学院，成都610031)

超弹性镍钛形状记忆合金单轴相变棘轮行为的宏观唯象本构模型1)

周 廷2)阚前华 康国政3)邱 博

(西南交通大学力学与工程学院，成都610031)

超弹性镍钛形状记忆合金因其良好的力学性能以及独特的超弹性和形状记忆效应已广泛应用于土木工程、航空航天和生物医疗等多个领域，在实际服役环境中超弹性镍钛合金元件不可避免地会承受不同应力水平的循环载荷作用，亟待建立描述相变棘轮行为(即峰值应变和谷值应变随着正相变和逆相变循环的进行不断累积)的循环本构模型.为此，基于已有的超弹性镍钛形状记忆合金在不同峰值应力下的单轴相变棘轮行为实验研究结果，在广义黏塑性框架下，对Graesser等提出的通过背应力非线性演化方程反映超弹性镍钛形状记忆合金超弹性行为的一维宏观唯像本构模型进行了拓展，考虑了正相变和逆相变过程中特征变量的差异及其随循环的演化，以非弹性应变的累积量为内变量引入了正相变开始应力、逆相变开始应力、相变应变和残余应变的演化方程，同时通过峰值应力与正相变完成应力的比值来确定演化方程中的相关系数，建立了描述超弹性镍钛合金单轴相变棘轮行为的本构模型.将模拟结果与对应的实验结果进行对比发现，建立的宏观唯像本构模型能够合理地描述超弹性镍钛形状记忆合金的单轴相变棘轮行为及其峰值应力依赖性，模型的预测结果和实验结果吻合得很好.

镍钛合金,相变棘轮行为,广义黏塑性,本构模型

引言

自从镍钛形状记忆合金 (SMA)问世以来，因其良好的力学特性以及独有的超弹性和形状记忆效应，一直受到了人们的广泛重视[13].该合金在加卸载过程中会发生奥氏体与马氏体的相互转化，从而体现出超弹性特性.由于其具有很高的能量输出能力，可作为减震智能元件并已广泛应用于土木工程结构中[46].在实际应用过程中，镍钛形状记忆合金材料不可避免地会受到循环载荷的作用，该合金的耗散能力随着循环周次的增加而急剧降低，从而导致其功能性失效.为此，诸多学者进行了超弹性镍钛形状记忆合金材料循环变形实验,研究其在循环载荷作用下的变形特征和超弹性劣化机理.Miyazaki等[7]，Lagoudas和Bo[8]，Sehitoglu等[9]对超弹性镍钛形状记忆合金进行的拉伸与卸载循环变形实验研究表明：随着循环周次的增加，相变开始应力和耗散能逐渐降低，相变硬化模量和残余应变逐渐增加，且最终趋于饱和.此后，进一步相关实验研究工作揭示了超弹性退化对温度[1012]、加载应力水平[1314]、加载路径[1517]、加载速率[1819]和原子比[2021]等因素的依赖性.Kang等[13]将镍钛形状记忆合金循环变形过程中的超弹性退化和相关应变值的循环累积现象定义为相变棘轮行为，并讨论了超弹性镍钛形状记忆合金相变棘轮行为的外加应力依赖性.

由于不同的材料体现出不同力学响应，需要建立不同本构模型进行描述[2225].对于镍钛形状记忆合金材料，从不同尺度可建立细观力学模型[2627]和宏观唯象模型[2829].其中，Graesser等[30]在Ozdemir模型[31]的基础上提出的镍钛形状记忆合金一维唯象本构模型因其形式简单且参数便于确定的优点，在镍钛形状记忆合金的结构分析中获得广泛应用.针对该模型无法描述镍钛形状记忆合金变形行为的率相关性、超弹性的相变约束行为和循环变形行为等，后续学者分别对其进行了必要的改进[3234].

然而，由于镍钛形状记忆合金器件在实际服役环境中承受的应力通常是非均匀的分布，应力水平变化很大，会涉及到不同峰值应力的循环载荷作用.已有的实验研究[1314]也表明,不同峰值应力的循环载荷作用下镍钛形状记忆合金的力学响应有很大差别.Kan和Kang[35]在广义塑性框架上建立了可以描述超弹性镍钛形状记忆合金单轴相变棘轮行为的宏观唯象本构模型，但该模型不能合理地描述外加峰值应力大于相变完成应力时的循环变形行为.

为此，本文基于Graesser模型[30]，通过引入新的与相变棘轮行为相关的演化方程及其对应力水平的依赖关系方程，建立了超弹性镍钛形状记忆合金单轴宏观唯象循环本构模型，可合理描述该合金在宽应力范围内的循环变形行为，包括超弹性退化效应.

1 实验结果

本文的主要内容是在已有实验结果基础上建立相应的本构模型，但是为了内容的完整性以及对所建立的本构模型进行合理性评价，本节将对 Song等[14]的实验结果进行简单的总结，突出超弹性镍钛形状记忆合金单轴相变棘轮行为对加载峰值应力水平的依赖性.为了更清楚地对相变棘轮行为变量演化进行描述，定义了如下参量：相变开始应力、逆相变开始应力、最大相变应变εL、残余应变εr以及耗散能Wd，如图1所示.

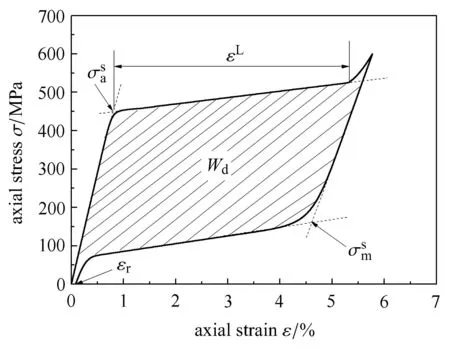
图1 相变棘轮行为的特征变量示意图Fig.1 Illustration of characteristic variables of transformation ratcheting

Song等[14]对超弹性镍钛合金微管进行了不同峰值应力水平的循环拉伸与卸载实验，结果如图2和图3所示.需要指出的是，为了便于和理论预测结果进行直接比较，图2中同时给出了本构模型的预测结果.由图2可见，超弹性镍钛形状记忆合金在不同峰值应力的循环拉伸与卸载作用下的相变棘轮行为体现出明显的峰值应力水平相关性.此外，峰值应力的大小会影响峰值应变是否达到最大相变应变.例如，如图2(a)所示，当峰值应力为500MPa时，在循环第1周并没有完全相变，但随着循环周次的增加，相变开始应力逐渐降低，到第5周时则发生了完全相变.

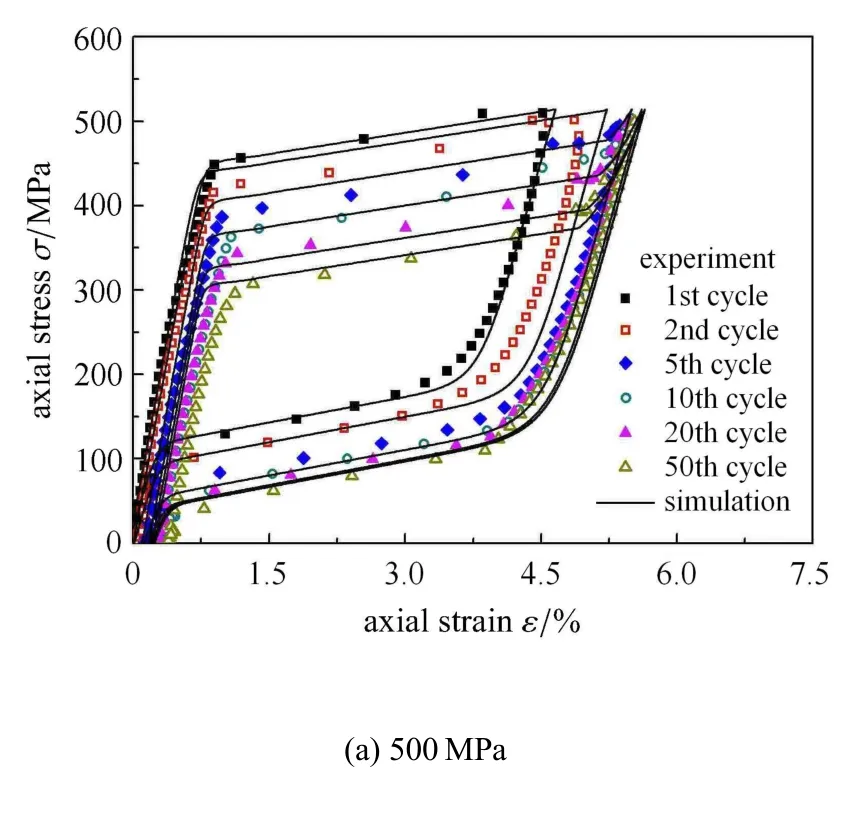
图2 不同峰值应力下的实验和模拟应力--应变曲线Fig.2 Experimental and simulated stress-strain curves with di ff erent peak stresses

同时，应力峰值的不同还会导致相变开始应力、逆相变开始应力、残余应变和最大相变应变均随循环周次的增加发生不同程度的演化，如图3所示.

图3 特征量循环演化曲线Fig.3 Evolution curves of characteristic variables

由图3可知，峰值应力越大，残余应变越大，但相变开始应力、逆相变开始应力和最大相变应变却越小；除相变开始应力和最大相变应变的初始值与应力峰值无关外，其余均与峰值应力相关；相变开始应力、逆相变开始应力、残余应变和最大相变应变均随循环周次的增加呈近似呈指数形式演化，除残余应变随循环周次的增加而增加外，其余特征量均随之减小，它们最终均趋于饱和.

2 本构模型

2.1 Graesser模型

Graesser等[30]在Ozdemir模型[31]基础上提出了描述镍钛形状记忆合金超弹性行为的一维唯象本构模型，通过背应力的变化来描述该合金的超弹性现象.具体的本构方程为

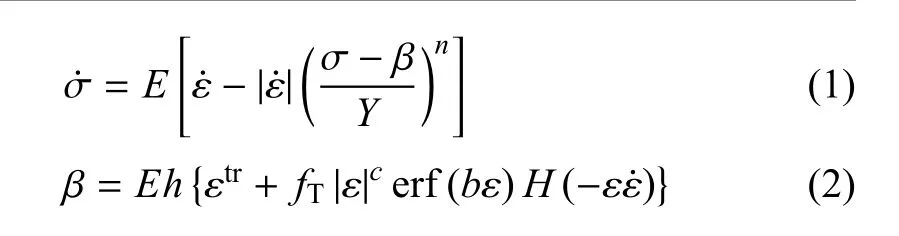
其中，σ和ε分别为应力和应变；E为弹性模量；Y为各向同性变形抗力，表征相变开始的临界应力；n是控制相变开始应力附近应力--应变曲线尖锐程度的材料参数，只能取正奇数；β为背应力；h为控制应力--应变曲线中相变段斜率的常数；εtr为相变应变.fT,b,c为材料常数.erf(·)为误差函数，可保证卸载后逆相变完成时残余应变为零，而参数b决定了逆相变完成后卸载段的形状；H(·)为Heaviside函数，用于控制卸载过程中逆相变的发生.Graesser等[30]提出的本构方程描述的超弹性镍钛形状记忆合金的应力--应变曲线如图4所示.

图4 Graesser模型描述的镍钛合金单轴应力--应变曲线Fig.4 Stress-strain curves of NiTi shape memory alloy described by Graesser’s model

由图4可见,Graesser模型存在以下几点不足：(1)该模型没有相变约束条件，即无论在多大的外载作用下，相变都不会结束，也就无法反映马氏体相变完成后的弹性变形阶段，这显然不符合超弹性NiTi形状记忆合金实际的的变形响应；(2)卸载时没有发生与试验一致的逆相变过程.这是由于该模型中表征相变应力的各向同性变形抗力Y的值并没有在加载和卸载中有所区分；(3)不能描述如图2和图3所示实验结果中所揭示的循环变形行为.

2.2 改进模型

如引言中所述，尽管文献[32-34]对Graesser本构方程进行了改进，但这些本构模型都主要针对应变控制循环加卸载的情况，无法合理预测如图2和图3所示的应力控制循环变形过程中单轴相变棘轮行为及其峰值应力水平相关性.在杨强军等[34]提出的循环相变模型基础上，笔者通过引入一些新的演化方程，对Graesser本构模型进行拓展，使之能够合理地描述超弹性镍钛形状记忆合金的单轴相变棘轮行为.具体方程如下：

加载段(奥氏体向马氏体转变)

卸载段(马氏体向奥氏体转变)

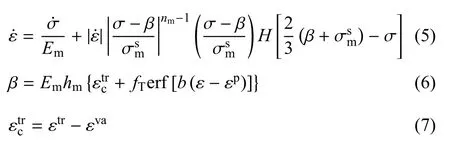
其中，Ea为奥氏体弹性模量，Em为马氏体弹性模量，为相变开始应力，为共同控制逆相变开始应力，fm和k为控制马氏体非线性弹性变形曲线的常数，εp为卸载过程中的残余应变.

由方程(3)～方程(7)可知，改进模型的应力与应变关系依然延续Graesser模型，总的应变增量包括弹性应变增量和非弹性应变增量，在本构方程的背应力中引入非弹性应变，包括相变应变、塑性应变和残余应变.与杨强军等[34]的模型相比，相变完成时的应变除了单轴下马氏体相变的最大相变应变εL外，还包括前一个循环周次的谷值应变εva和弹性应变εe；除考虑残余应变的循环累积作用外，在背应力中引入当前循环周次非弹性应变代替非弹性应变，定义为当前循环周次的非弹性应变减去前一循环周次的谷值应变εva.

ha和hm分别为正相变和逆相变的硬化参数，定义为

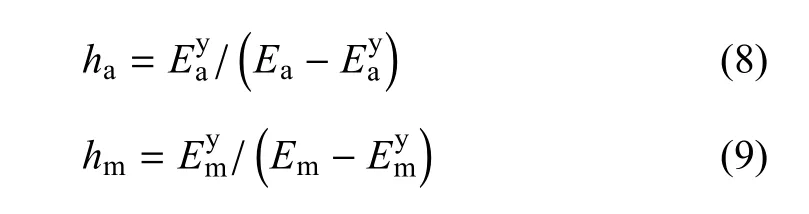
图3所示的实验结果表明，超弹性镍钛形状记忆合金在循环变形过程中的相变开始应力、逆相变开始应力和最大相变应变随循环周次呈指数演化.因此，引入如下演化方程进行描述

其中，CL,Ca,Cm为非线性演化系数，含有下标0的量表示相应参数的初始值，含有下标“sat”的量表示相应参数循环稳定后的饱和值.

残余应变随循环周次的增加呈现指数衰减且强烈依赖于加载峰值应力水平.因此，在不考虑马氏体塑性变形的情况[14]，引入如下残余应变的演化方程

其中，εmax为残余应变的稳定值，σp为加载的峰值应力，和σ为相变开始应力和相变结束应力，M np为残余应变的应力相关系数，bp为控制残余应变的饱和速率

Kan和Kang[35]的模型中将相变棘轮行为的应力相关性体现在相变诱发塑性应变和残余马氏体分数上，当峰值应力大于相变完成应力时，应力影响系数保持不变.因此，无法反映峰值应力大于相变完成应力后的加载应力水平相关性，且没有考虑图2和图3中所示的相变开始应力和最大相变应变的饱和值以及逆相变应力的初始值和饱和值均与峰值应力水平有关的实验现象.为此，本文以峰值应力与相变完成应力的比值表示其变形程度，并令它们满足如下的方程

其中，h1至h12为对应参数的应力相关系数，m为峰值应力与相变结束应力的比值.

2.3 参数确定

本构模型中的材料参数的确定可以采用如下方法：

图5 参数确定示意图Fig.5 The schematic diagram of parameters determination

(3)演化系数CL,Ca,Cm可通过对实验获得的最大相变应变、向前相变开始应力和逆相变开始应力随循环周次变化的演化曲线进行非线性拟合得到；εmax,bp,np取自文献[14].

(4)需要指出的是，以上参数是通过峰值应力为800MPa的实验结果得到的.针对式(14)～式(17)中的应力相关参数h1～h12，则需要根据不同峰值应力下的相关变量的初值和饱和值，通过式(14)～式(17)的拟合而得，如图6所示.

3 模型验证

为了验证模型的合理性，在按2.3节中的方法确定了如表1所示的材料参数后，利用提出的模型对超弹性镍钛形状记忆合金在不同峰值应力下的相变棘轮行为进行了模拟，模拟结果如图2所示.

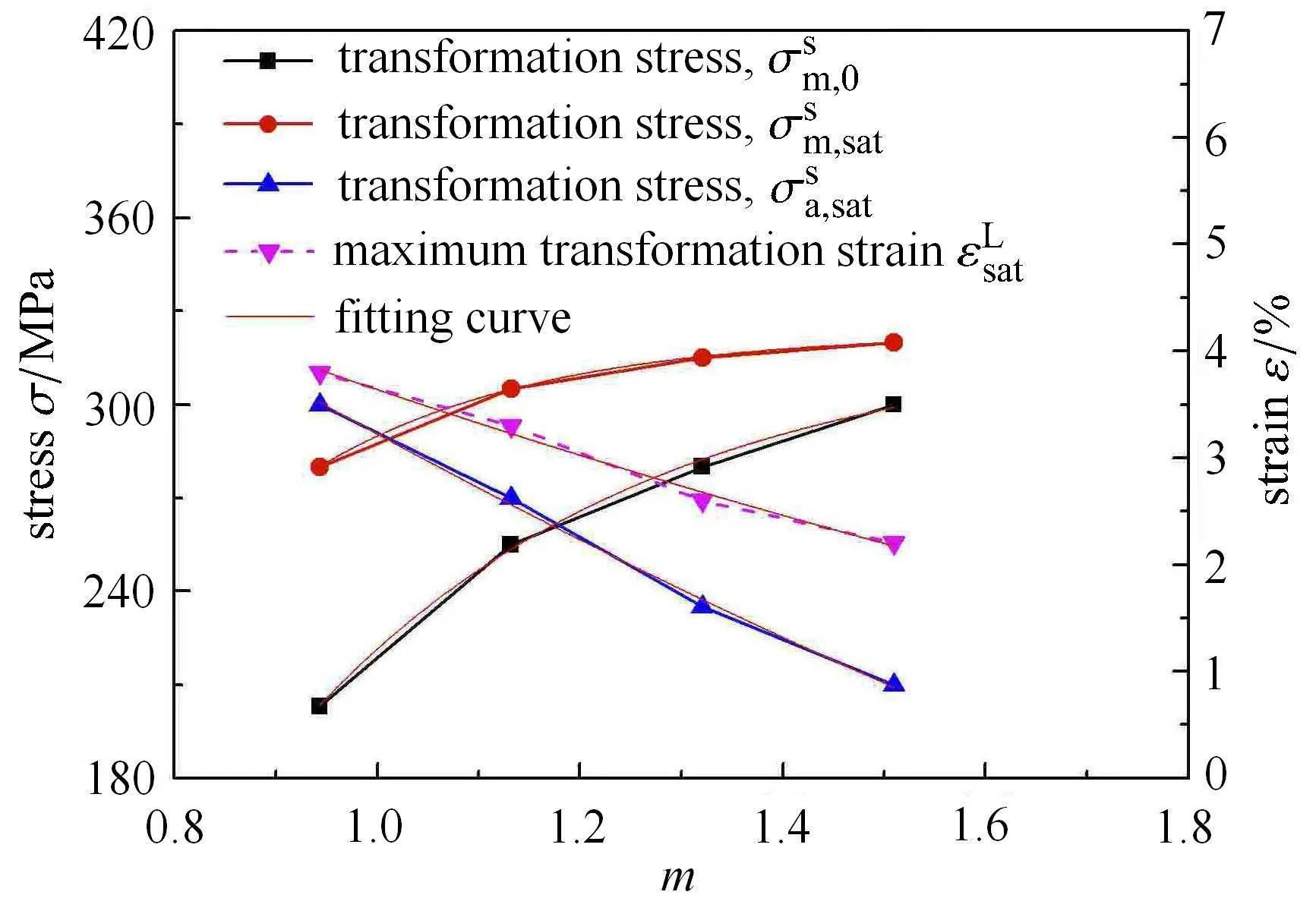
图6 应力相关系数的确定Fig.6 The determination of stress-related coefficients

表1 镍钛形状记忆合金微管的材料参数Table 1 Material parameters used in the proposed model for NiTi shape memory micro-tube

由图2可见：提出模型预测的循环应力--应变曲线与实验结果吻合较好，并且合理地反映了超弹性镍钛形状记忆合金在不同峰值应力下的单轴相变棘轮行为.另外，通过相变开始应力和逆相变开始应力、最大相变应变和残余应变新的演化方程的引入，合理地描述了它们随循环周次增加而逐渐演化且在一定的循环周次后达到饱和状态的实验现象.

另外，改进模型的模拟结果也合理地反映了在超弹性镍钛形状记忆合金循环变形过程中体现出的超弹性退化现象，对实验中得到的峰值应变和残余应变随循环周次增加，而耗散能随循环周次增加显著下降的演化规律进行了很好的理论预测，如图7所示.当然，从图2和图7给出的理论预测结果和实验结果的直接对比可以看出，两者的变化规律吻合较好，但在具体数值上,模型预测结果和实验结果之间还有一些差别，特别是针对耗散能的预测.

图7 残余应变、峰值应变和耗散能随循环演化的实验和模拟对比Fig.7 The comparison of the evolution of residual strain,peak strain and dissipation energy with circulation between experiment and simulation

为了进一步体现改进模型的合理性，首先将该模型对一个加卸载循环下的模拟结果与Graesser模型模拟结果进行了对比，结果如图4所示.由图4可知，改进模型由于施加了相变约束，建立了加/卸载过程独立的马氏体演化方程，可以很好地描述马氏体正相变和逆相变过程，以及马氏体相变完成后的弹性变形.

进一步将改进模型和杨等模型对相变棘轮行为的模拟进行对比 (不考虑式 (13)～式 (18)，改进模型即可退化到杨等模型).图8给出了杨等模型模拟的不同应力幅值下的循环应力--应变响应曲线.对比图2和图8可以看出，当应力水平处于相变刚结束时，改进模型和杨等模型均可准确地预测相变棘轮行为；当应力水平提高到800MPa时，杨等[34]提出的模型由于没有引入加载应力水平相关的演化方程，无法准确模拟峰值应变和残余应变的循环累积.

图8 杨等模型[34]描述的不同应力幅值下的镍钛合金单轴应力--应变曲线Fig.8 Stress-strain curves under di ff erent stress amplitude of NiTi shape memory alloy described by Yang’s model[34]

需要指出的是，所改进的循环本构模型尽管可准确预测相变棘轮行为，但所引入的方程均为宏观唯象描述，未考虑相变棘轮行为的微观变形机理，还需要在当前发展的模型基础上开展进一步研究，更加充分地揭示镍钛形状记忆合金的循环变形机理，建立基于微观变形机理的本构模型，更加准确地预测相变棘轮行为，促进该合金在工程中的应用.

4 结论

根据不同峰值应力水平下超弹性镍钛形状记忆合金单轴相变棘轮行为的实验结果，通过引入一些新的参量演化方程(即相变开始应力、逆相变开始应力、残余应变和最大相变应变演化方程)对Graesser模型进行了改进，提出了一个新的、可以合理反映超弹性镍钛形状记忆合金单轴相变棘轮行为的加载峰值应力水平依赖性的一维宏观唯象循环本构模型.通过提出模型的预测结果和相应实验结果的对比表明，提出的本构模型能够对超弹性镍钛形状记忆合金的单轴相变棘轮行为及其超弹性性能的循环劣化现象进行合理的预测.

1 Buehler WJ,Gilfrich JV,Wiley RC.E ff ects of low-temperature phase changes on the mechanical properties of alloys near composition TiNi.Journal of Applied Physics,1963,34(5)：1475-1477

2 Duerig TW,Pelton A,St¨ockel D.An overview of nitinol medical applications.Materials Science and Engineering:A,1999,273-275(99)：149-160

3 Morgan NB.Medical shape memory alloy applications—the market and its products.Materials Science and Engineering:A,2004,378(1)：16-23

4钱辉,李宏男,宋钢兵.形状记忆合金阻尼器消能减震体系的控制研究.振动与冲击,2008,27(8)：42-47(Qian Hui,Li Hongnan,Song Gangbing.Energy dissipation system of structures with shape memory alloy damper.Journal of Vibration and Shock,2008,27(8)：42-47(in Chinese))

5 Shin M,Andrawes B.Experimental investigation of actively confine concrete using shape memory alloys.Engineering Structures,2010,32(3)：656-664

6邵红红,彭玉婷,姜秀英等.医用镍钛合金表面多层薄膜的制备及摩擦磨损和耐腐蚀性能.功能材料,2014,45(4)：14145-14149(Shao Honghong,Peng Yuting,Xiu ying,et al.Preparation of multilayers on the surface of medical NiTi alloy and properties of friction/wear and corrosion resistance.Journal of Functional Materials,2014,45(4)：14145-14149(in Chinese))

7 Miyazaki S,Imai T,Igo Y,et al.E ff ect of cyclic deformation on the pseudoelasticity characteristics of Ti-Ni alloys.Metallurgical transactions A,1986,17(1)：115-120

8 Lagoudas DC,Bo Z.Thermomechanical modeling of polycrystalline SMAs under cyclic loading,Part II：Material characterization and experimental results for a stable transformation cycle.International Journal of Engineering Science,1999,37(9)：1141-1173

9 Sehitoglu H,Anderson R,Karaman I,et al.Cyclic deformation behavior of single crystal NiTi.Materials Science and Engineering:A,2001,314(1)：67-74

10 Lexcellent C,Bourbon G.Thermodynamical model of cyclic behaviour of Ti-Ni and Cu-Zn-Al shape memory alloys under isothermal undulated tensile tests.Mechanics of Materials,1996,24(1)：59-73

11 Nemat-Nasser S,Guo WG.Superelastic and cyclic response of NiTi SMA at various strain rates and temperatures.Mechanics of Materials,2006,38(5)：463-474

12 Yu C,Kang G,Kan Q.A physical mechanism based constitutive model for temperature-dependent transformation ratchetting of NiTi shape memory alloy：One-dimensional model.Mechanics of Materials,2014,78(78)：1-10

13 Kang GH,Kan QH,Qian LM,et al.Ratchetting deformation of super-elastic and shape-memory NiTi alloys.Mechanics of Materials,2009,41(2)：139-153

14 Song D,Kang GZ,Kan QH,et al.The e ff ect of martensite plasticity on the cyclic deformation of super-elastic NiTi shape memory alloy.Smart Materials and Structures,2014,23(1)：5008

15 Saleeb AF,Padula SA,Kumar A.A multi-axial,multimechanism based constitutive model for the comprehensive representation of the evolutionary response of SMAs under general thermomechanical loading conditions.International Journal of Plasticity,2011,27(5)：655-687

16 Wang X,Wang Y,Lu Z,et al.An experimental study of the superelastic behavior in NiTi shape memory alloys under biaxial proportional and non-proportional cyclic loadings.Mechanics of Materials,2010,42(3)：365-373

17 Song D,Kang GZ,Kan QH,et al.Non-proportional multiaxial transformationratchettingofsuper-elasticNiTishapememoryalloy：Experimental observations.Mechanics of Materials,2014,70(1)：94-105

18 Shaw JA,Kyriakides S.Thermomechanical aspects of NiTi.Journal of the Mechanics and Physics of Solids,1995,43(8)：1243-1281

19 Morin C,Moumni Z,Zaki W.Thermomechanical coupling in shape memory alloys under cyclic loadings：Experimental analysis and constitutive modeling.International Journal of Plasticity,2011,27(12)：1959-1980

20 Strnadel B,Ohashi S,Ohtsuka H,et al.Cyclic stress-strain characteristics of Ti-Ni and Ti-Ni-Cu shape memory alloys.Materials Science and Engineering:A,1995,202(1)：148-156

21 Strnadel B,Ohashi S,Ohtsuka H,et al.E ff ect of mechanical cycling on the pseudoelasticity characteristics of Ti-Ni and Ti-Ni-Cu alloys.Materials Science and Engineering：A,1995,203(1)：187-196

22万征,姚仰平,孟达.复杂加载下混凝土的弹塑性本构模型.力学学报，2016,48(5)：1159-1171(Wan Zheng,Yao Yangping,Meng Da.An elastoplastic constitutive model of concrete under complicated load.Chinese Journal of Theoretical and Applied Mechanics,2016,48(5)：1159-1171(in Chinese))

23陈庆,朱合华,闫治国等.基于自洽法的电化学沉积修复饱和混凝土细观描述.力学学报,2015,47(2)：367-371(Chen Qing,Zhu Hehua,Yan Zhiguo,et al.Micro-scale description of the saturatedconcrete repaired by electrochemical deposition method based on self-consistent method.Chinese Journal of Theoretical and Applied Mechanics,2015,47(2)：367-371(in Chinese))

24谈炳东,许进升,贾云飞等.短纤维增强EPDM包覆薄膜超弹性本构模型.力学学报,2017,49(2)：317-323(Tan Bingdong,Xu Jinsheng,Jia Yunfei,et al.Hyperelastic constitutive model for short fibe reinforced EPDM inhibitor film Chinese Journal of Theoretical and Applied Mechanics,2017,49(2)：317-323(in Chinese))

25黄小双,彭雄奇,张必超.帘线/橡胶复合材料各向异性黏–超弹性本构模型.力学学报,2016,48(1)：140-145(Huang Xiaoshuang,Peng Xiongqi,Zhang Bichao.An anisotropic visco-hyperelastic constitutive model for cord-rubber composites.Chinese Journal of Theoretical and Applied Mechanics,2016,48(1)：140-145(in Chinese))

26 Lagoudas DC,Entchev PB.Modeling of transformation-induced plasticity and its e ff ect on the behavior of porous shape memory alloys.Part I：constitutive model for fully dense SMAs.Mechanics of Materials,2004,36(9)：865-892

27 Yu C,Kang GZ,Kan QH,et al.Rate-dependent cyclic deformation of super-elastic NiTi shape memory alloy：thermo-mechanical coupled and physical mechanism-based constitutive model.International Journal of Plasticity,2015,72：60-90

28 Manchiraju S,Anderson PM.Coupling between martensitic phase transformations and plasticity：a microstructure-based finit element model.International Journal of Plasticity,2010,26(10)：1508-1526

29 Yu C,Kang GZ,Kan QH,et al.A micromechanical constitutive model based on crystal plasticity for thermo-mechanical cyclic deformation of NiTi shape memory alloys.International Journal of Plasticity,2013,44(9)：161-191

30 Graesser E,Cozzarelli F.A proposed three-dimensional constitutive model for shape memory alloys.Journal of Intelligent Material Systems and Structures,1994,5(5)：78-89

31¨Ozdemir H.Nonlinear transient dynamic analysis of yielding structures.[PhD Thesis].University of Califormia Berkeley,1976

32 Ren WJ,Li HN,Song GB.A one-dimensional strain-rate-dependent constitutive model for superelastic shape memory alloys.Smart Materials and Structures,2007,16(1)：191-197

33钱辉,李宏男,宋钢兵等.基于塑性理论的形状记忆合金本构模型、试验和数值模拟.功能材料,2007,38(7)：1114-1118(Qian Hui,Li Hongnan,Song Gangbing,et al.Constitutive model of shape memory alloy based on plastic theory：experiment and simulation.Journal of Functional Materials,2007,38(7)：1114-1118(in Chinese))

34杨强军,阚前华,康国政等.超弹性NiTi合金循环相变诱发塑性本构模型.功能材料,2015,46(10)：10018-10022(Yang Qiangjun,Kan Qianhua,Kang Guozheng,et al.Constitutive model on cyclic transformation included plasticity of super-elastic NiTi alloy.Journal of Functional Materials,2015,46(10)：10018-10022(in Chinese))

35 Kan QH,Kang GZ.Constitutive model study on transformation ratcheting of superelastic NiTi alloy.International Journal of Plasticity,2010,26(3)：441-464

A MACROSCOPIC PHENOMENOLOGICAL CONSTITUTIVE MODEL FOR THE UNIAXIAL TRANSFORMATION RATCHETING OF SUPER-ELASTIC NiTi SHAPE MEMORY ALLOY1)

Zhou Ting2)Kan Qianhua Kang Guozheng3)Qiu Bo
(School of Mechanics and Engineering，Southwest Jiaotong University，Chengdu 610031，China)

Super-elastic NiTi shape memory alloy(SMA)has been extensively used in many field such as civil engineering,aerospace and bio-medical field due to its good mechanical properties,including unique super-elasticity and shape memory e ff ect.In practical applications,the SMA-based devices are unavoidable subjected to cyclic loadings at di ff erent stress levels.However,it is necessary to establish a cyclic constitutive model to describe the transformation ratcheting behavior,i.e.,the peak strain and valley strain accumulate cyclically during forward transformation and reverse transformation.Based on the existing experimental results of the transformation ratchetting of the super-elastic NiTishape memory alloy obtained under the stress-controlled cyclic tension-unloading tests with di ff erent peak stresses,the one-dimensional macroscopic phenomenological constitutive model of super-elastic NiTi shape memory alloy proposed by Graesser,where super-elastic behavior is reflecte by the nonlinear evolution equation of back stress,was extended to describe the uniaxial transformation ratchetting within the framework of generalized visco-plasticity.In the extended model,the di ff erences of characteristic variables and their evolutions between the forward transformation and reverse transformation were considered,the evolution equations of the start stress of forward transformation,the start stress of reverse transformation,maximum transformation strain and residual strain were introduced by the internal variable of relative accumulated inelastic strain.In the meantime,the correlation coefficients in these evolution equations were determined by the ratio of the peak stress and the finis stress of forward transformation.The comparison of the experiments and simulations shows that the extended model can reasonably describe the dependence of uniaxial transformation ratchetting of super-elastic NiTi shape memory alloy on the peak stress,and the simulated results are in good agreement with the experimental ones.

NiTi alloy,transformation ratcheting,generalized visco-plasticity,constitutive model

O348.3

：A

10.6052/0459-1879-17-116

2017–04–05 收稿，2017–05–10 录用,2017–05–13 网络版发表.

1)国家自然科学基金资助项目(11532010,11202171).

2)周廷，在读博士，主要研究方向：智能材料本构关系研究.E-mail：zhouting16@foxmail.com

3)康国政，教授，主要研究方向：先进材料本构关系研究.E-mail：guozhengkang@126.com

周廷,阚前华,康国政,邱博.超弹性镍钛形状记忆合金单轴相变棘轮行为的宏观唯象本构模型.力学学报,2017,49(3)：588-596

ZhouTing,KanQianhua,KangGuozheng,QiuBo.Amacroscopicphenomenologicalconstitutivemodelfortheuniaxialtransformation ratcheting of super-elastic NiTi shape memory alloy.Chinese Journal of Theoretical and Applied Mechanics,2017,49(3)：588-596