应变局部化分析的嵌入强间断多尺度有限元法1)

卢梦凯 张洪武 郑勇刚

(大连理工大学，国际计算力学研究中心，工业装备结构分析国家重点实验室，运载工程与力学学部工程力学系，大连116024)

-固体力学

应变局部化分析的嵌入强间断多尺度有限元法1)

卢梦凯 张洪武 郑勇刚2)

(大连理工大学，国际计算力学研究中心，工业装备结构分析国家重点实验室，运载工程与力学学部工程力学系，大连116024)

固体材料的应变局部化行为是导致结构破坏失效的重要因素之一，开展相关数值模拟分析对于结构安全性评估具有重要意义.然而由于材料的非均质和多尺度特性，采用传统数值方法进行求解时通常需要从最小特征尺度离散求解的结构，这将大幅度增加计算规模和成本.针对这一问题，本文提出了一种基于嵌入强间断模型的多尺度有限元方法.该方法从粗细两个尺度离散求解模型，首先在细尺度单元上引入嵌入强间断模型来描述单元间断特性，所附加的跳跃位移自由度则通过凝聚技术进行消除，从而保持细尺度单元刚度阵维度不变.其次，提出了一种增强多节点粗单元技术，其可根据局部化带与粗单元边界相交情况自适应动态地增加粗节点，新构造的增强数值基函数可以捕捉细尺度间断特性，完成物理信息从细单元到粗单元的准确传递以及宏观响应的快速分析；再次，在细尺度解的计算中，将细尺度解分解为降尺度解与单胞局部摄动解，从而消除弹塑性分析时单胞内部的不平衡力.最后，通过两个典型算例分析，并与完全采用细单元的嵌入有限元结果进行对比，验证了所提出算法的正确性与有效性.

多尺度有限元法，嵌入强间断模型，应变局部化，增强粗单元，弹塑性分析

引言

应变局部化作为一种典型的破坏形式广泛存在于诸多工程材料与结构中，如金属拉伸颈缩、地基基础破坏、山体滑坡等.局部化问题的特点通常呈现为很大的塑性应变局限在一个狭小的细带内，随着局部化带的演化扩展，最终导致结构的失稳破坏.针对应变局部化问题的数值分析研究对预测材料与结构的承载力和稳定性具有重要的指导意义.

目前，已有许多计算方法用来模拟材料或结构的失效行为[16].模拟应变局部化或者断裂问题的方法必须考虑解的客观性，即网格无关性.而基于经典损伤或者塑性模型的方法，往往存在网格依赖性问题[7].为了解决这一问题，通常需要在模型中引入正则化机制.目前广泛采用的正则化模型主要分为两大类，其中一类是弥散型的正则化模型，主要包括非局部模型[89]、Cosserat模型[10]、率相关模型[11]和梯度塑性模型[1213]等.另一类则是离散型的模型，如扩展有限元(XFEM)[1,1416]、嵌入有限元(EFEM)[1722]、数值流形方法[23]等.其中EFEM是基于Simo等[24]所发展的假设增强应变(AES)框架提出的，其通过引入嵌入强间断模型来提供耗散机制[17].另外，EFEM分析时增加的单元附加自由度可以通过凝聚技术消除，由此可以保证单元刚度阵维数不变，便于程序实现.目前EFEM已被广泛应用于应变局部化和断裂破坏问题的模拟分析中.然而，随着工程分析要求的日益提高，尤其是针对大规模、非均质问题时，需要采用非常精细的网格对空间进行离散，这将导致计算量的大幅增大，从而限制了EFEM的大规模工程应用.

多尺度方法作为一种可有效解决此类问题的数值计算方法，已经成为近年来研究的热点，如计算均匀化方法[25]、两尺度渐近分析方法[26]、多尺度有限元方法[27]等.其中多尺度有限元方法由于其宏微观尺度之间信息传递方便准确而受到了广泛关注.多尺度有限元方法最早由Hou等[27]提出，其主要特点是引入了数值基函数的概念，从而可以方便地进行升尺度与降尺度计算.多尺度有限元法首先被用于多孔介质渗流分析[2829].Zhang等[30]将该方法推广到固体力学领域，并在许多问题中得到了应用，如动力问题[3132]、热力电耦合问题[33]、桁架非线性问题[34]、多相多孔介质耦合问题[32,35]和裂纹扩展问题[36]等，但其在连续体应变局部化的多尺度问题方面，还鲜有报道.

针对单相固体的应变局部化问题，本文提出了一种基于嵌入强间断模型的多尺度有限元方法.首先介绍了嵌入强间断模型的基本理论，包括控制方程、物理场描述、弱形式控制方程以及本构关系.其次，详细说明了所提出算法的基本思想和计算框架，主要包括细单元尺度上间断特性表征方式、升尺度计算中增强数值基函数构造方法、自适应多节点粗单元技术、降尺度计算中处理单胞内部不平衡力的局部摄动方法以及详细的算法实现流程.最后，用所提方法计算了两个局部化算例，与基于精细网格的EFEM解的对比结果表明了多尺度有限元方法的正确性与有效性.

1 嵌入强间断模型的基本理论

1.1 控制方程

本文主要研究二维问题.如图1所示，考虑一个二维平面有界区域Ω，被间断线Γ划分为区域Ω+和Ω-.描述小变形下固体强间断模型的控制方程可以写为

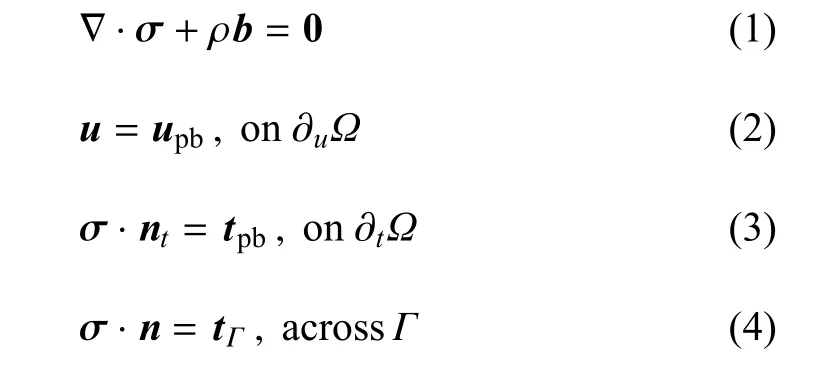
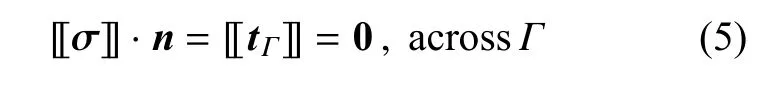
式中,∇为Nabla算子，σ为应力，ρ表示密度，b为体力向量，u为位移，upb为边界∂uΩ上的指定位移，tpb为边界∂tΩ上的指定力，nt为∂tΩ的外法向向量，n为Γ的法向向量，[[σ]]=σ+-σ-表示间断应力，σ+和σ-分别为间断线正向区域的应力和背向区域的应力，[[·]]代表间断运算符，tΓ代表间断线上的力矢量.

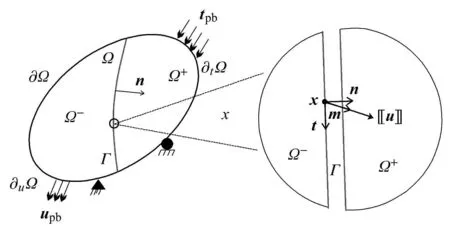
图1 强间断模型示意图Fig.1 Illustration of the strong discontinuity model

1.2 物理场描述

在强间断模型中，为了描述位移的间断特性，可将位移场u表示为

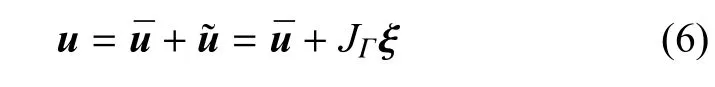
由式(6)可得应变场

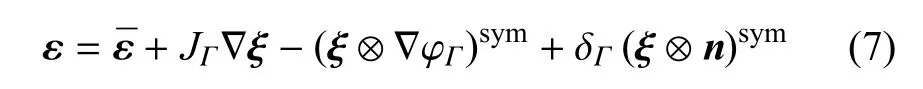
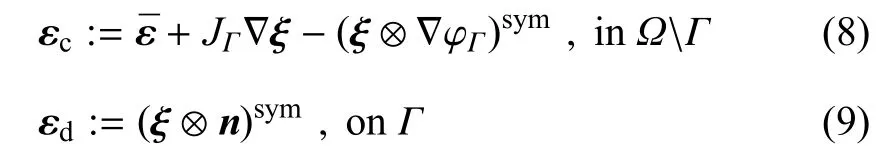
1.3 弱形式控制方程

对控制方程(1)运用虚功原理，同时考虑边界条件(2)～条件(5)，并运用分部积分法与非连续函数的散度定理(F代表不连续函数)，即

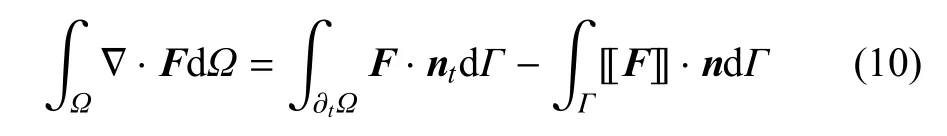
可以推得式(1)的弱形式(忽略重力项)

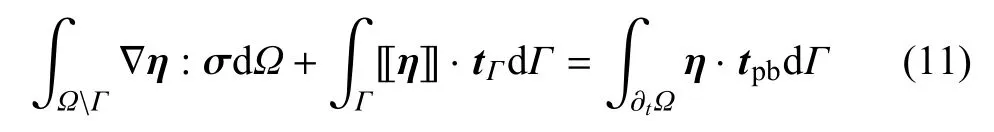
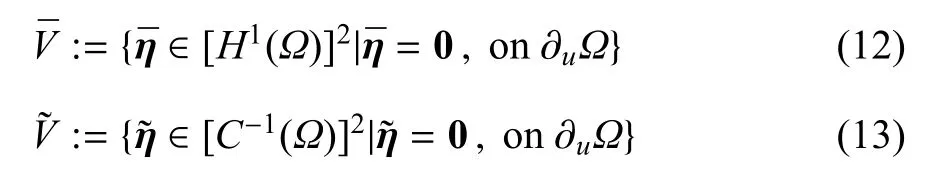
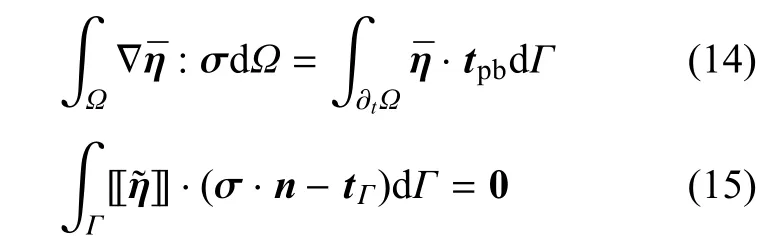
1.4 本构方程

在嵌入强间断模型中，连续区域内的应力σ与间断区域内的力tΓ的演化过程分别由以下两种本构模型确定：

(1)连续型Drucker-Prager塑性本构模型

在ΩΓ区域，采用屈服函数与塑性势函数相同的关联Drucker-Prager塑性模型，其屈服函数可以写作

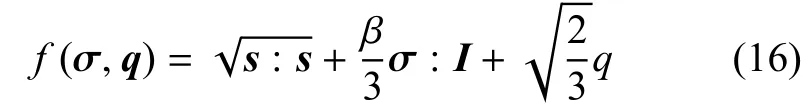
式中，s是σ的偏量部分；q=-σY-HCp，HC为塑性模量，p为等效塑性应变，σY为初始屈服应力，β为Drucker-Prager模型的材料参数，本文取为

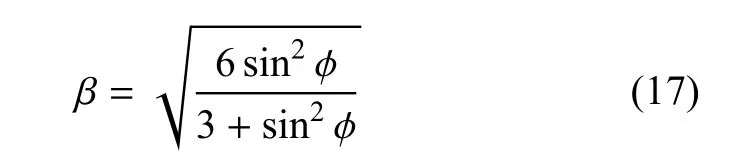
其中,φ为摩擦角.根据塑性流动理论，可以得到塑性应变率与内变量的演化方程

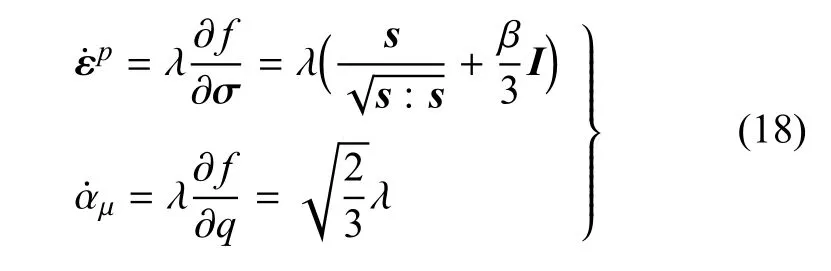
式中，λ为塑性乘子.基于加法分解下的应变率可以记为弹性应变率与塑性应变率之和，即

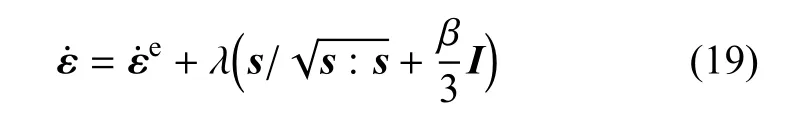
针对连续型塑性本构的积分算法，本文采用经典的向后欧拉返回映射算法，具体可参见文献[37-38].

(2)局部化型Drucker-Prager塑性本构

在连续型塑性本构里，塑性乘子λ是正则的，而在间断Γ区域，塑性乘子λ表现为奇异性，引入

结合式(7)～式(9)和式(18)，可以得到如下应力率的表达式

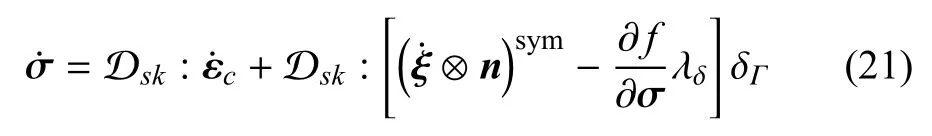
式中，Dsk为四阶弹性本构张量.结合应力率有界的条件，可进一步得到

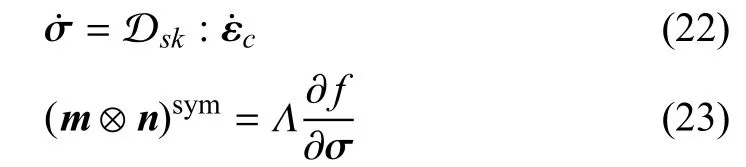
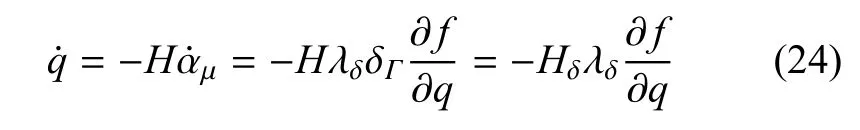
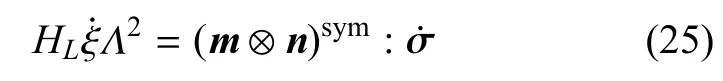
在局部坐标n-t下(如图1所示)，向量tΓm与可以表示为

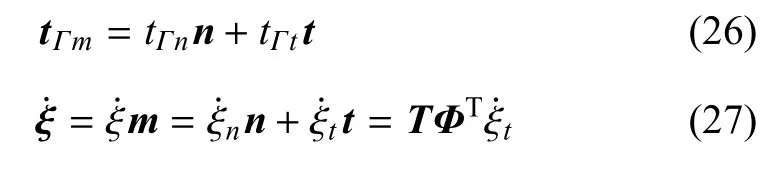
式中,tΓn= tΓm·n，tΓt= tΓm·t，T = [n t] 和其中χ=tanφ，且根据式(17)，可得

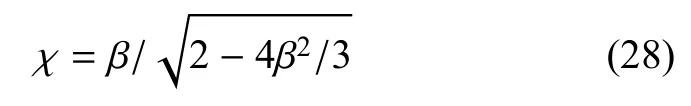
将式(26)～式(28)代入式(25)，可得间断Γ区域内的本构关系

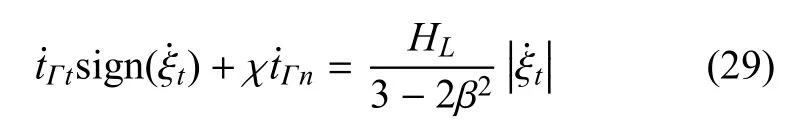
2 基于嵌入强间断模型的多尺度有限元法

本节中，我们结合嵌入强间断模型提出了一种用于处理单相固体局部化问题的多尺度有限元方法.其主要思想是将几何区域离散为粗单元与细单元，在细单元上用强间断模型描述间断特性，再通过构造增强的数值基函数，正确地将间断特性从细尺度传递到粗尺度上，从而进行局部化问题的多尺度有限元分析.以下给出了针对单相固体结合嵌入强间断模型的多尺度有限元方法基本框架，主要包括细尺度上的有限元离散、增强数值基函数的构造、粗尺度上的求解以及细尺度解的计算.

2.1 细尺度上的有限元离散

在细尺度上采用八节点等参单元进行离散，其位移可由节点位移插值得到，即

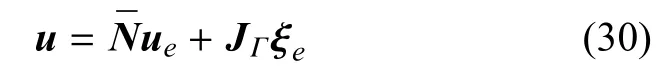
式中，ue与ξe分别为节点位移与间断跳跃量，¯N为标准形函数，JΓ为间断形函数，可写为

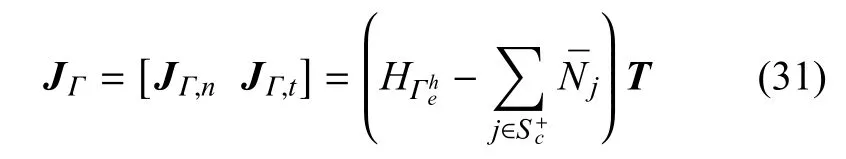
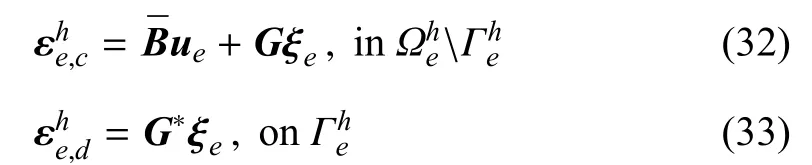
式中，应变算子¯B=∇sym¯N，协调算子G和投射算子G∗分别为

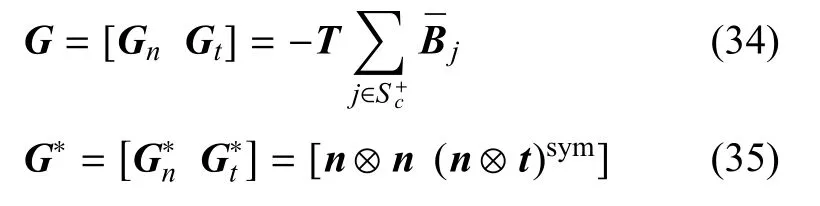
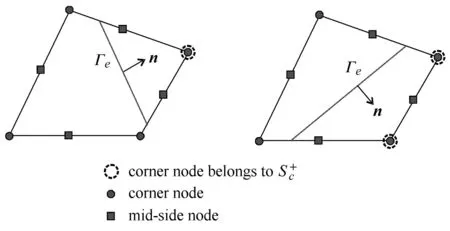
图2 局部化单元内角点集合的选取Fig.2 Selection for the corner nodes setin a discontinuous element

对控制方程弱形式(14)和式(15)进行Galerkin离散可得

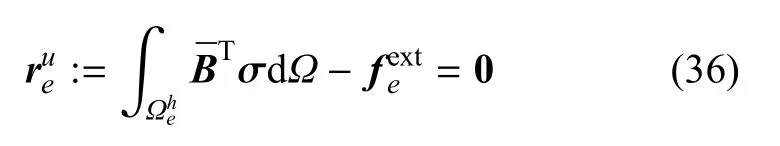
进一步对式(36)和式(37)进行线性化，并采用Newton-Raphson增量求解策略，可得到以节点位移增量δue和单元间断量δξe,t作为未知量的离散控制方程[17,21].

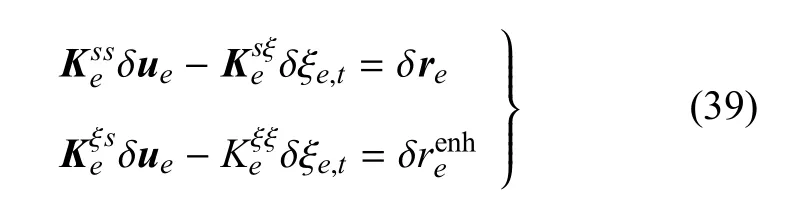
式中各矩阵具体表达式为

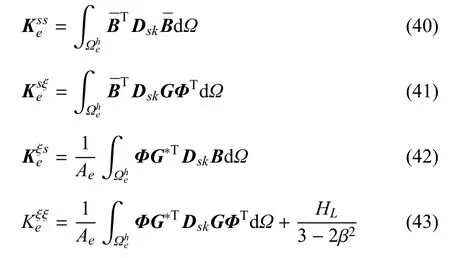
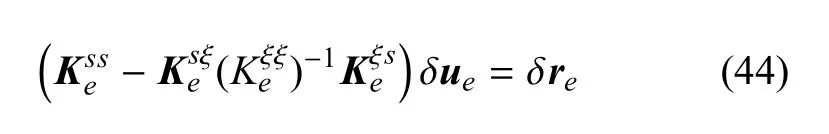
2.2 增强数值基函数的构造

考虑一个带有间断区域的多尺度单胞(如图3(a)所示)，其表示的粗单元在形式上也是一种多节点粗单元，但与常规多节点粗单元中一般采用等间隔布置粗节点的方式不同，其增加的粗节点位置与个数是根据间断ΓE与单胞边界的交点来确定的.如图3(a)中的粗节点9,10和11即为分析过程中随着间断区域演化而动态增加的粗节点.该类粗单元所构造的数值基函数称为增强数值基函数，其可以正确地传递细尺度单元上所描述的间断特性，从而保证了局部化问题多尺度分析时的有效性.

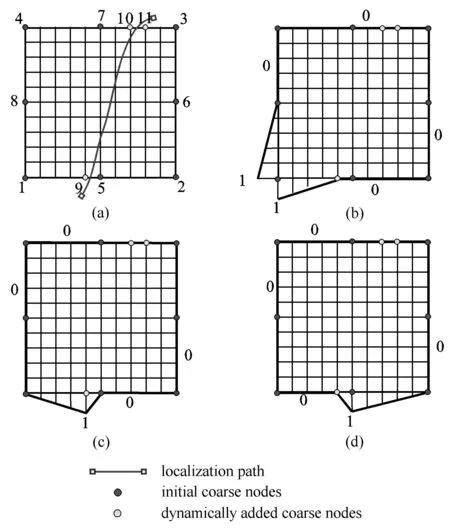
图3 (a)多节点粗单元，(b)～(d)分别为1号、9号和5号粗节点的边界指定位移分布图Fig.3(a)a multi-node coarse element,the distributions of the prescribed boundary values for(b)coarse node 1,(c)coarse node 9 and(d)coarse node 5

增强数值基函数的构造方式同常规的多节点粗单元类似.记粗单元对应的单胞整体等效刚度阵为为刚度阵组装算子，Sne为单胞内细单元数目.则构造j号粗节点的k向自由度对应的数值基函数Njk时，需满足下式

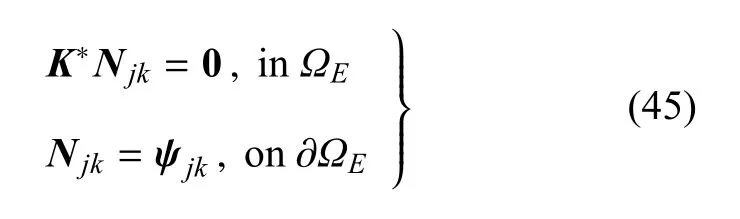
式中,ψjk是Njk在边界∂ΩE上的指定值.本文采用多节点线性边界条件来进行构造，图3(b)给出了构造N1k时ψ1k的分布，即当k为ux时，边界上细节点的uy都约束为0，ux在线段19和18上施加峰值为1的线性分布位移；当k为uy时，边界上细节点的ux都约束为0，uy在线段19和18上施加峰值为1的线性分布位移.ψ9k和ψ5k的分布由图3(c)和图3(d)所示.类似地，可以获得整个粗单元下所对应边界条件ψ的分布，并求解得到增强数值基函数N.

至此，可以建立起细单元节点自由度与粗单元节点自由度之间的关系如下

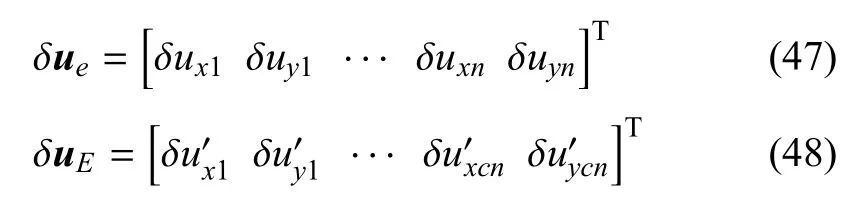
式中，n是单胞内的细节点数目，δue和δuE分别为细单元与粗单元上的节点增量位移向量.在实际计算时，若出现剪切带与粗单元边界相交时，使拥有该边界的相邻粗单元同时成为增强粗单元，并共享增强节点，从而保证相邻粗单元间位移的协调.

2.3 粗尺度上的求解

在获得了增强数值基函数N之后，就可以用其形成单胞的等效刚度矩阵与右端不平衡力向量，可以分别表示为

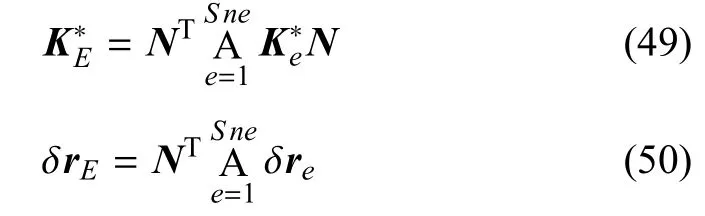
其中,A为组装单元矩阵或向量的集成算子[29].粗尺度下的整体刚度矩阵与右端不平衡力向量可以写作

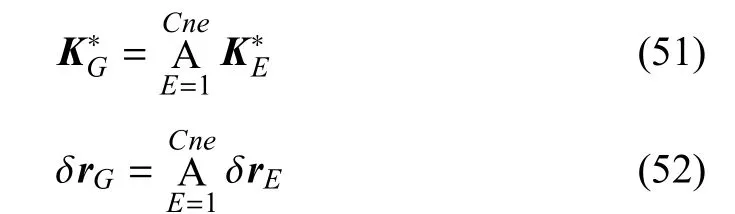
其中,Cne代表粗单元数目.最终，粗尺度下的增量位移解可由求得.

2.4 细尺度解的计算

在获得整体宏观解δuG后，可以得到每个单胞的宏观解δuE，再通过降尺度计算来获得降尺度解而在多尺度有限元的非线性分析中，其细尺度解δuuc可以表示为降尺度解与局部摄动解之和，即

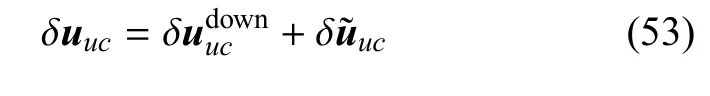
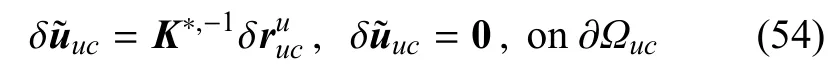
3 算法实现

本节中，我们给出了所提出算法的具体实现步骤.

(一)将几何体离散为细单元与粗单元，设置材料参数、算法参数等.

(二)计算每个单胞的等效刚度阵，计算数值基函数.

(三)对时间步n进行循环.

(1)n=n+1.

(2)对迭代步k进行循环.

①k=k+1.

②重新计算那些细单元刚度阵改变的单胞数值基函数，并根据式(51)和式(52)分别形成新的和

(a)对于 ΩΓ区域，采用连续型 Drucker-Prager塑性本构关系，用经典的向后欧拉返回映射算法进行更新[37-38].

(b)对于Γ区域，采用局部型Drucker-Prager塑性本构关系，用非标准的返回映射算法进行更新[19].

⑤判断是否满足Eu＜或k达到指定的最大迭代数的条件.如果满足，则进入步骤(四)；否则，返回步骤①.

(四)用下式判断是否有细单元进入局部化[19]

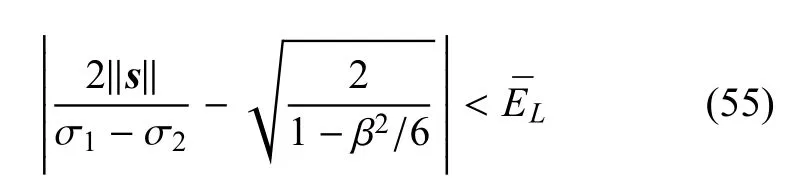
式中，σ1和σ2分别为第一和第二主应力，¯EL为算法参数.如果有新单元进入局部化，则运行间断线跟踪算法[39]，并动态增加所在粗单元的节点，计算增强数值基函数；否则，直接进入步骤(五).

(五)判断n是否为最大时间步.如果是，则进入步骤(六)；否则，返回步骤(1).

(六)计算结束，输出结果.

在步骤⑤中，收敛判断准则Eu定义为

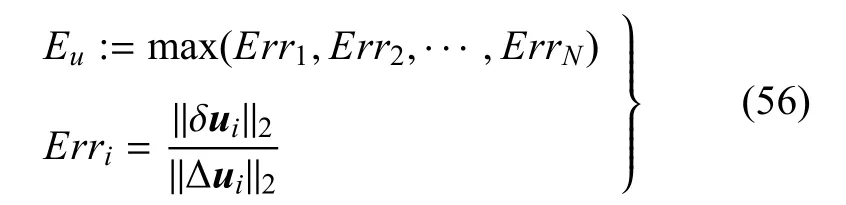
式中,N为细网格节点总数(实际计算时去掉位移为零的自由度).

4 算例分析

本节用所提出算法来模拟二维平面应变下的单相固体应变局部化问题，并考虑不同数目粗节点的粗单元的计算效力，所得结果与采用细单元的EFEM参考解进行对比.此外，两个算例均采用直接位移控制算法来控制加载，收敛精度参数¯Eu和¯EL分别取为10-6和10-3.

4.1 土柱的竖直压缩

模型尺寸为0.04m×0.14m，底部节点全约束，在上表面施加竖直向下位移0.1mm.将整个模型离散为4×14个单胞，每个单胞离散为8×8个细单元.采用4种不同节点的粗单元：CE4,CE8,CE4E和CE8E(CEnE中CE代表粗单元，n代表粗单元节点个数，E代表采用增强数值基函数技术)对所提出算法进行考察，如图4所示.表1给出了具体的材料参数，在分析中采用50个载荷步进行加载.

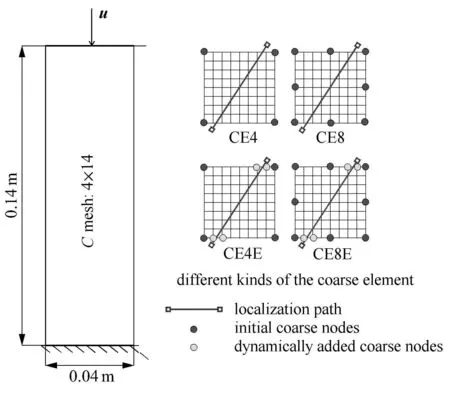
图4 土柱压缩算例示意图Fig.4 Illustration of the compression test of soil column

表1 土柱材料参数Table 1 Material parameters for the column

图5给出了4种类型粗单元的多尺度有限元解与EFEM参考解的作用反力与加载位移变化曲线.从图中可以看出，采用常规粗单元CE4与CE8的曲线并没与呈现出结构软化现象，而采用CE4E与CE8E的结果则与参考解吻合很好.该结果表明增强数值基函数可以正确地捕捉细单元上的间断特性，从而获得有效的计算结果.图6给出了CE4E,CE8E和参考解的竖直位移云图.3种方法得到的结果吻合良好.另一方面，针对不同方法的CPU花费时间比CE4E/EFEM和CE8E/EFEM分别为0.37和0.42，这也表明了多尺度有限元方法在计算效率上的优势.需要进一步指出的是，对于大规模工程问题而言，其应变局部化区域相对于整体结构而言比本算例更小，本文所发展的多尺度有限元方法计算效率将会大幅度提高.

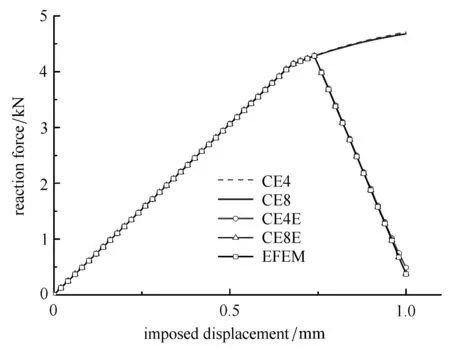
图5 不同方法作用反力与加载位移的结果比较Fig.5 Results of the reaction force versus the imposed displacement with di ff erent methods

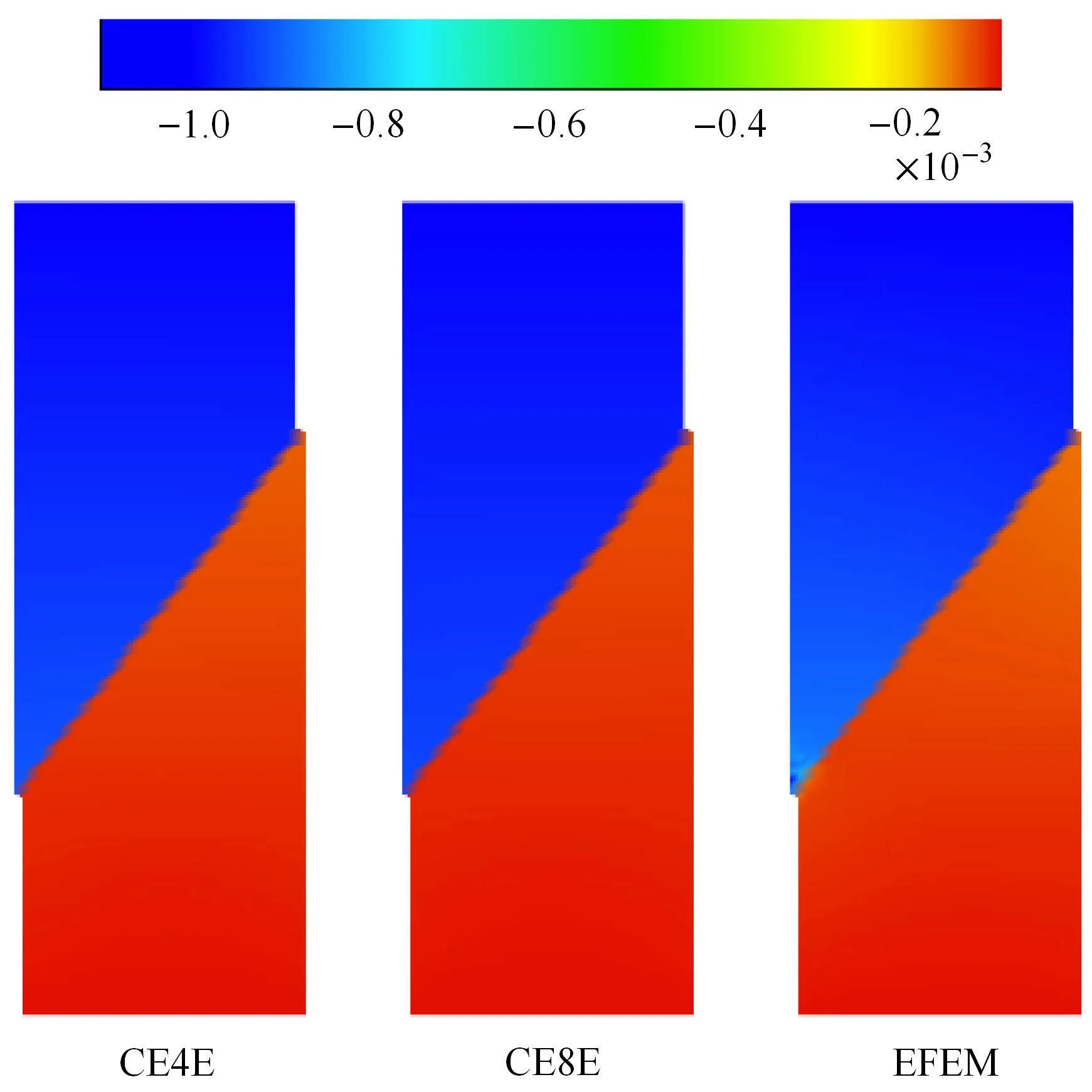
图6 不同方法竖直位移的云图Fig.6 Contours of the vertical displacement with di ff erent methods

4.2 基础的水平加载

本算例模拟了基础在水平位移作用下的局部化问题.模型尺寸为10m×10m，底部节点竖直方向位移约束，左侧节点位移全约束，在右侧刚性块中心处作用水平方向的位移载荷0.15m.整个基础离散为10×10个单胞，每个单胞离散为6×6个细单元，采用两种不同节点的粗单元：CE4E和CE8E，具体见图7所示.表2列出了具体的材料参数.水平载荷设置成50个载荷步进行加载.

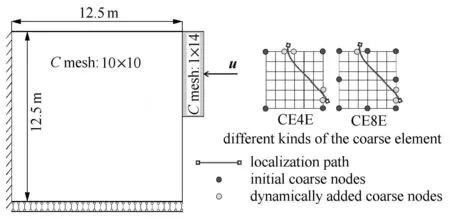
图7 基础水平加载算例示意图Fig.7 Illustration of the horizontal loading test of the foundation

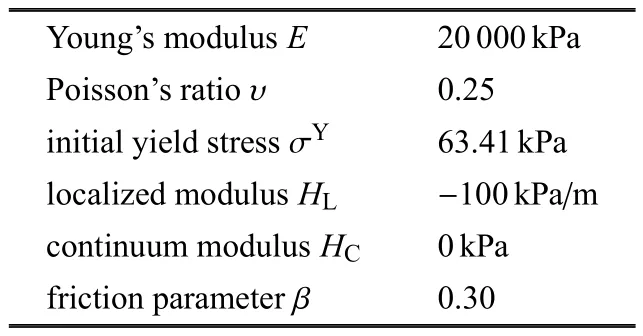
表2 基础材料参数Table 2 Material parameters for the foundation

图8给出了采用CE4E、CE8E和EFEM作用反力与水平位移的变化曲线.从图中可以发现，两种粗单元CE4E与CE8E的结果都与EFEM结果吻合非常好，且CE8E的结果较CE4E更加接近于EFEM参考解.该结果表明随着粗节点的增加，可以有效地提高解的精度.图9给出了不同时刻(A～D分别对应图8不同时刻)下基于CE8E预测获得的局部化带扩展图.图10给出了CE4E、CE8E和参考解的水平位移云图.从图中局部化带的位置与形状分析，可以发现3种方法得到的结果吻合良好.另外，CE4E/EFEM和CE8E/EFEM的CPU花费时间比分别为0.40和0.47.

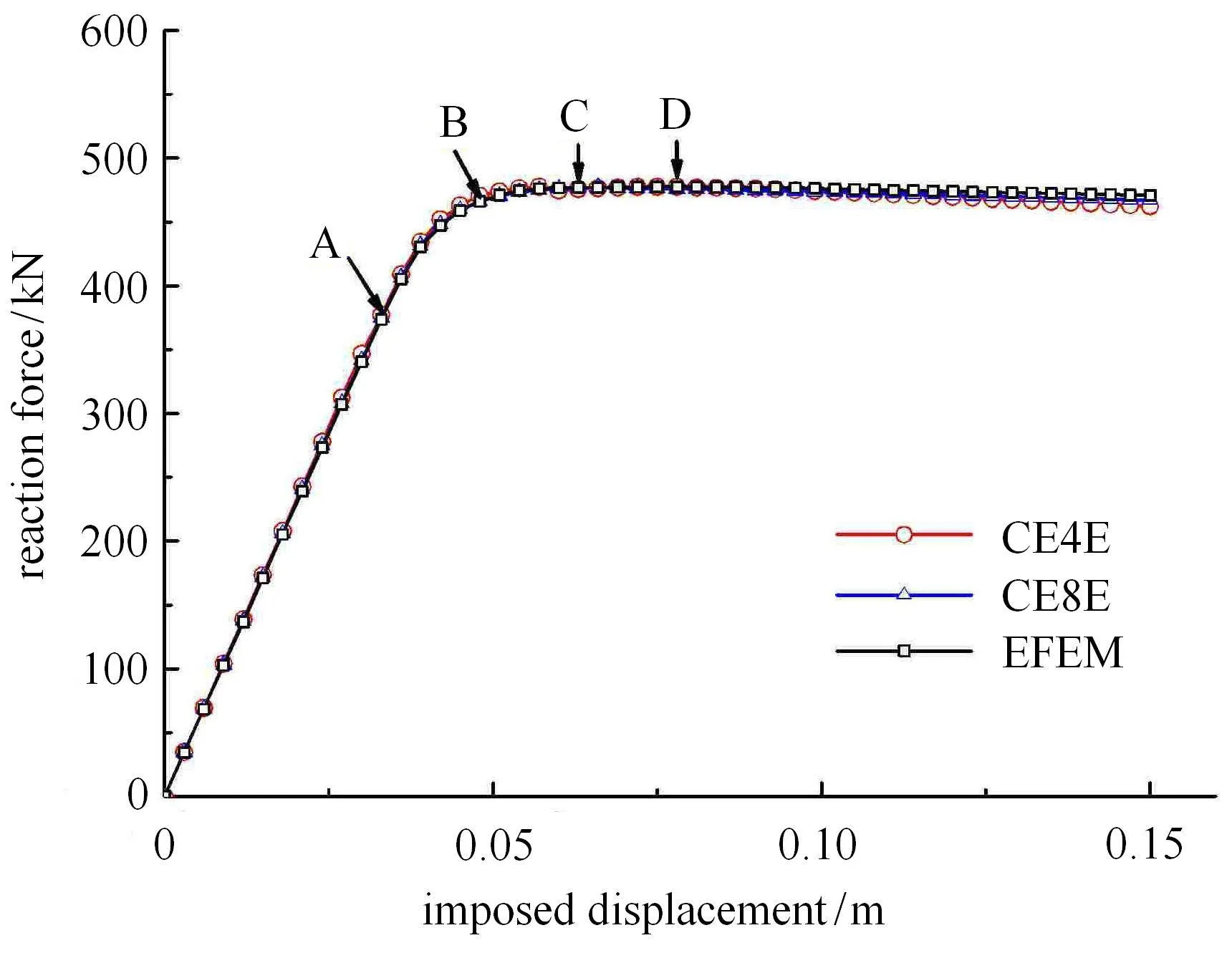
图8 不同方法作用反力与加载位移的结果比较Fig.8 Results of the reaction force versus the imposed displacement with di ff erent methods

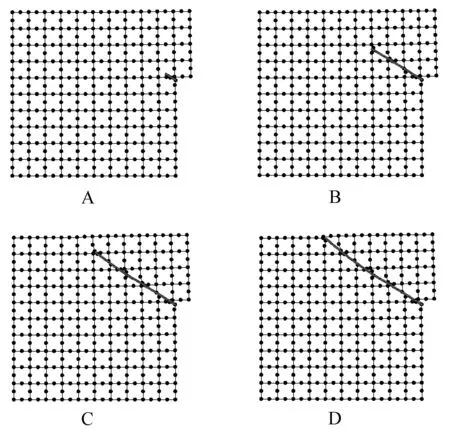
图9 CE8E获得的局部化带扩展图(A～D对应于图8中的不同时刻，此图中变形放大了5倍)Fig.9 Illustrations of localization band propagation with the CE8E(A～D correspond to di ff erent times in Fig.8,the deformation is scaled by 5 for clarity)

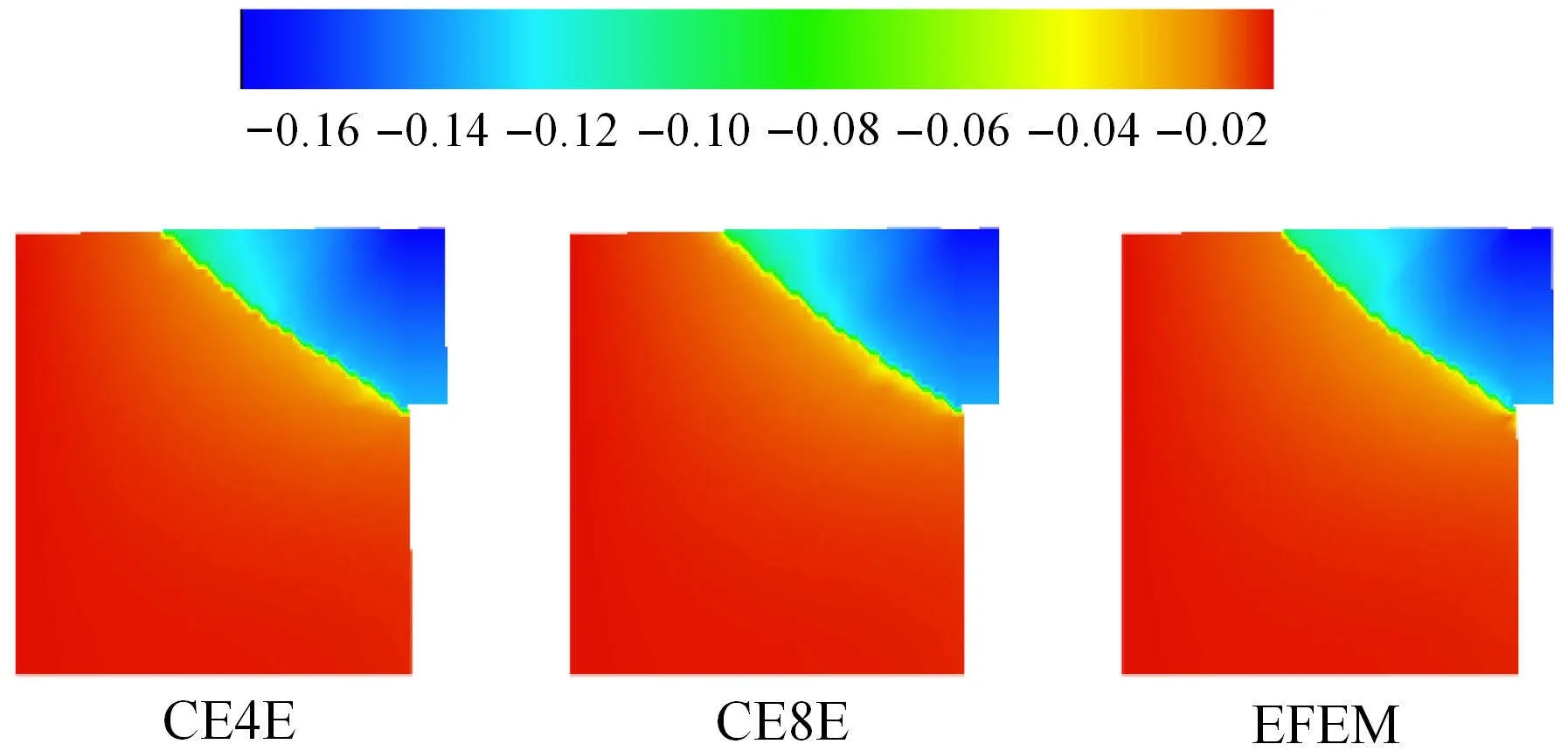
图10 不同方法水平位移的云图Fig.10 Contours of the horizontal displacement with di ff erent methods

5 结论

本文提出了一种针对单相固体应变局部化分析的多尺度有限元方法.首先，在细单元内引入嵌入强间断模型，并通过凝聚技术在单元级别上消除间断自由度，使得整体多尺度算法流程可以保持不变且易于程序实现；其次，对于具有局部化细单元的单胞提出了一种增强的多节点粗单元，其可以动态地根据间断位置来增加粗节点个数，构造的增强数值基函数可以正确捕捉细尺度上的间断特性；然后，在细尺度解的计算中，应用局部摄动法来消除单胞内部的不平衡力.最后，通过两个应变局部化算例，验证了所提出算法的正确性与有效性.此外，该方法可以较容易地推广用于处理多场多相强间断问题.

1 Belytschko T,Black T.Elastic crack growth in finit elements with minimal remeshing.International Journal for Numerical Methods in Engineering,1999,45(5)：601-620

2 Schrefle BA,Secchi S,Simoni L.On adaptive refinemen techniques in multi-fielproblems including cohesive fracture.Computer Methods in Applied Mechanics and Engineering,2006,195(4-6)：444-461

3 Miehe C,Mauthe S.Phase fielmodeling of fracture in multiphysics problems.Part III.Crack driving forces in hydro-poroelasticity and hydraulic fracturing of fluid-saturate porous media.Computer Methods in Applied Mechanics and Engineering,2016,304：619-655

4 Chen Z,Hu W,Shen L,et al.An evaluation of the MPM for simulating dynamic failure with damage di ff usion.Engineering Fracture Mechanics,2002,69(17)：1873-1890

5 Yang PF,Gan Y,Zhang X,et al.Improved decohesion modeling with the material point method for simulating crack evolution.International Journal of Fracture,2014,186(1-2)：177-184

6 Boyce BL,Kramer SLB,Fang HE,et al.The Sandia Fracture Challenge：blind round robin predictions of ductile tearing.International Journal of Fracture,2014,186(1-2)：5-68

7 Bazant ZP,Belytschko T.Wave propagation in a strain-softening bar：Exact solution.Journal of Engineering Mechanics,1985,111：381-389

8 Pijaudier-Cabot G,Bazant ZP.Nonlocal damage theory.Journal of Mechanical Engineering,1987,113：1512-1533

9 Wol ffC,Richart N,Molinari JF.A non-local continuum damage approach to model dynamic crack branching.International Journal for Numerical Methods in Engineering,2015,101(12)：933-949

10李锡夔,唐洪祥.压力相关弹塑性Cosserat连续体模型与应变局部化有限元模拟.岩石力学与工程学报,2005,24(9)：1497-1505(Li Xikui,Tang Hongxiang.Pressure-dependent elasto-plastic Cosserat continuum model and finit element simulation of strain localization.Chinese Journal of Rock Mechanics and Engineering,2005,24(9)：247-253(in Chinese))

11 Needleman A.Material rate dependence and mesh sensitivity in localization problems.Computer Methods in Applied Mechanics and Engineering,1988,67(1)：69-85

12 de Borst R,M¨uhlhaus HB.Gradient-dependent plasticity：Formulation and algorithmic aspects.International Journal for Numerical Methods in Engineering,1992,35(3)：521-539

13 Peerlings RHJ,de Borst R,Brekelmans WAM,et al.Gradient enhanced damage for quasi-brittle materials.International Journal for Numerical Methods in Engineering,1996,39(19)：3391-3403

14 Dolbow J,Mo¨es N,Belytschko T.Discontinuous enrichment in fi nite elements with a partition of unity method.Finite Elements in Analysis and Design,2000,36(3-4)：235-260

15庄茁,成斌斌.发展基于CB壳单元的扩展有限元模拟三维任意扩展裂纹.工程力学,2012,29(6)：12-21(Zhuang Zhuo,Cheng Binbin.Development of X-FEM on CB shell element for simulating 3D arbitrary crack growth.Engineering Mechanics,2012,29(6)：12-21(in Chinese))

16石路杨,余天堂.多裂纹扩展的扩展有限元法分析.岩土力学,2014,35(1)：263-272(Shi Luyang,Yu Tiantang.Analysis of multiple crack growth using extended finit element method.Rock and Soil Mechanics,2014,35(1)：263-272(in Chinese))

17 Simo JC,Oliver J,Armero F.An analysis of strong discontinuities induced by strain-softening in rate-independent inelastic solids.Computational Mechanics,1993,12(5)：277-296

18 Armero F.On the characterization of localized solutions in inelastic solids：an analysis of wave propagation in a softening bar.Computer Methods in Applied Mechanics and Engineering,2001,191(3-5)：181-213

19 Borja RI,Regueiro RA.Strain localization in frictional materials exhibiting displacement jumps.Computer Methods in Applied Mechanics and Engineering,2001,190(20-21)：2555-2580

20 Benkemoun N,Gelet R,Roubin E,et al.Poroelastic two-phase material modeling：theoretical formulation and embedded finit element method implementation.International Journal for Numerical and Analytical Methods in Geomechanics,2015,39(12)：1255-1275

21 Linder C,Armero F.Finite elements with embedded strong discontinuities for the modeling of failure in solids.International Journal for Numerical Methods in Engineering,2007,72(12)：1391-1433

22郑利涛,胡志强,唐洪祥.强间断分析方法在土工结构物渐进破坏过程中的应用.岩土力学,2012,33(9)：2771-2780(Zheng Litao,Hu Zhiqiang,Tang Hongxiang.Application of strong discontinuity analysis to progressive failure process of geotechnical structures.Rock and Soil Mechanics,2012，33(9)：2771-2780(in Chinese))

23徐栋栋,郑宏,杨永涛等.多裂纹扩展的数值流形法.力学学报,2015,47(3)：471-481(Xu Dongdong,Zheng Hong,Yang Yongtao et al.Multiple crack propagation based on the numerical manifold method.Chinese Journal of Theoretical and Applied Mechanics,2015,47(3)：471-481(in Chinese))

24 Simo JC,Rifai MS.A class of mixed assumed strain methods and the method of incompatible modes.International Journal for Numerical Methods in Engineering,1990,29(8)：1595-1638

25 Kouznetsova V,Geers MGD,Brekelmans WAM.Multi-scale constitutive modelling of heterogeneous materials with a gradientenhanced computational homogenization scheme. International Journal for Numerical Methods in Engineering,2002,54(8)：1235-1260

26 Yang ZQ,Cui JZ,Sun Y,et al.Multiscale computation for transient heat conduction problem with radiation boundary condition in porous materials.Finite Elements in Analysis and Design,2015,102：7-18

27 Hou TY,Wu XH.A multiscale finit element method for elliptic problemsincompositematerialsandporousmedia.JournalofComputational Physics,1997,134(1)：169-189

28 Dostert P,Efendiev Y,Hou TY.Multiscale finit element methods for stochastic porous media fl w equations and application to uncertainty quantification Computer Methods in Applied Mechanics and Engineering,2008,197(43-44)：3445-3455

29 Efendiev Y,Hou TY.Multiscale Finite Element Methods.[s.l.]：Springer Science&Business Media,2009

30 Zhang HW,Wu JK,Fu ZD.Extended multiscale finitelement method for elasto-plastic analysis of 2D periodic lattice truss materials.Computational Mechanics,2010,45(6)：623-635

31卓小翔,刘辉,楚锡华等.非均质材料动力分析的广义多尺度有限元法.力学学报,2016,48(2)：378-386(Zhuo Xiaoxiang,Liu Hui,Chu Xihua,et al.A generalized multiscale finit element method for dynamic analysis of heterogeneous material.Chinese Journal ofTheoretical and Applied Mechanics,2016,48(2)：378-386(in Chinese))

32张洪武,卢梦凯,郑勇刚.非均质饱和多孔介质弹塑性动力分析的广义耦合扩展多尺度有限元法.计算力学学报,2016,33(4)：454-461(Zhang Hongwu,Lu Mengkai,Zheng Yonggang.General coupling extended multi-scale finit element method for the elastoplastic dynamic analysis of heterogeneous saturated porous media.Chinese Journal of Computational Mechanics,2016,33(4)：454-461(in Chinese))

33 Lv J,Yang K,Zhang HW,et al.A hierarchical multiscale approach for predicting thermo-electro-mechanical behavior of heterogeneous piezoelectric smart materials.Computational Materials Science,2014,87：88-99

34 Liu H,L¨u J.An equivalent continuum multiscale formulation for 2D geometrical nonlinear analysis of lattice truss structure.Composite Structures,2017,160：335-348

35 Zhang HW,Lu MK,Zheng YG,et al.General coupling extended multiscale FEM for elasto-plastic consolidation analysis of heterogeneous saturated porous media.International Journal for Numerical and Analytical Methods in Geomechanics,2015,39(1)：63-95

36 Lu MK,Zhang HW,Zheng YG,et al.A multiscale finit element method with embedded strong discontinuity model for the simulation of cohesive cracks in solids.Computer Methods in Applied Mechanics and Engineering,2016,311：576-598

37 Simo JC,Hughes TJR.Computational Inelasticity.[s.l.]：Springer Science&Business Media,2006

38 de Souza Neto EA,Peric D,Owen DRJ.Computational Methods for Plasticity.New Jersey：John Wiley&Sons,2011

39 ParvanehSM,FosterCD.Onnumericalaspectsofdi ff erentupdating schedules for tracking fracture path in strain localization modeling.Engineering Fracture Mechanics,2016;152：26-57

EMBEDDED STRONG DISCONTINUITY MODEL BASED MULTISCALE FINITE ELEMENT METHOD FOR STRAIN LOCALIZATION ANALYSIS1)

Lu Mengkai Zhang Hongwu Zheng Yonggang2)
(International Research Center for Computational Mechanics，State Key Laboratory of Structural Analysis for Industrial Equipment，Department of Engineering Mechanics，Dalian University of Technology，Dalian 116024，China)

Strain localization is a common factor that may lead to the failure of solid structure and its numerical analysis becomes an important aspect for the structural safety evaluation.Due to the heterogeneity and multiscale nature,however,traditional numerical methods need to resolve the structure at the fin scale to obtain reasonable results,which increases drastically the computational scale and cost.To solve this problem,an embedded strong discontinuity model based multiscale finit element method is proposed here.In this method,both coarse and fin scale elements are used to represent the structure.The embedded strong discontinuity model is firs introduced into the fin element to describe the discontinuity and the corresponding additional displacement jump degree of freedom on the elemental level can be eliminated with the condensation technique,which keeps the dimensions of the sti ff ness matrix unchanged.Then,an enhanced multi-node coarse element technique is proposed,which can adaptively insert coarse nodes according to the intersection between the discontinuity line and coarse element boundary and thus guarantees the proper transformation ofinformation between the fin and coarse elements.The problem can then be e ff ectively solved on the coarse scale level.Moreover,a solution decomposition technique,in which the fin scale solution is decomposed into the downscaling and local perturbation solutions,is adopted to eliminate the unbalance forces within the unit cell in the elasto-plastic analysis.Finally,two representative examples are presented to demonstrate the accuracy and e ff ectiveness of the proposed method through the comparisons with the results of the embedded finit element method.

multiscale finit element method,embedded strong discontinuity model,strain localization,enhanced coarse element,elasto-plastic analysis

O242.21,O344.3

：A

10.6052/0459-1879-16-397

2016–12–27 收稿，2017–03–12 录用,2017–03–13 网络版发表.

1)国家自然科学基金(11232003,11672062)和中央高校基本科研业务费(DUT14YQ217)资助项目.

2)郑勇刚，教授，主要研究方向：多尺度与多场耦合计算力学.E-mail：zhengyg@dlut.edu.cn

卢梦凯，张洪武，郑勇刚.应变局部化分析的嵌入强间断多尺度有限元法.力学学报,2017,49(3)：649-658

Lu Mengkai,Zhang Hongwu,Zheng Yonggang.Embedded strong discontinuity model based multiscale finit element method for strain localization analysis.Chinese Journal of Theoretical and Applied Mechanics,2017,49(3)：649-658