岩土的一种强度准则及其变换应力法1)

万 征 秋仁东 郭金雪

(中国建筑科学研究院地基基础研究所，北京100013)

岩土的一种强度准则及其变换应力法1)

万 征2)秋仁东 郭金雪

(中国建筑科学研究院地基基础研究所，北京100013)

基于岩土摩擦性，假设岩土破坏是由其物理空间内特征面上的应力比决定，提出了等效应力比的概念，即物理空间特征面上的剪应力合力与正应力合力的比值.在二维条件下，等效应力比可表示为σ-τ坐标系下与摩尔圆相切的直线扣除截距正切值；在三维条件下，假设在XYZ空间内存在一三维物理空间平面，此三维空间特征平面的等效应力比为影响材料强度特性的决定性因素，基于上述三维空间特征面建立了强度准则并称之为a准则.SMP准则以及广义Mises准则都是a准则的特例，当二维坐标中的截距为零时，则强度准则退化为SMP(spatially mobilized plane)强度准则，而当正切角为零时，则强度准则退化为广义Mises准则.而当截距与外切角均不为零时，则强度准则为介于上述两者之间的一种强度准则,在偏平面上为介于SMP曲边三角形与广义Mises圆形之间的曲边三角形.在子午面上，采用考虑岩土压剪耦合的屈服准则，破坏准则采用幂函数表达式.在偏平面上提出了基于a准则的形状函数，并采用真三维应力状态表示的破坏强度准则表示在三轴压缩路径下以p,q二维应力变量表达的准则公式，推导得到了基于a准则的变换应力公式，可简单地将一般以p,q为基本变量的二维模型转变为三维应力模型.通过强度以及多种应力路径的测试对比，验证了a准则及基于该准则的变换应力公式的合理性.

岩土材料，破坏，强度准则，屈服准则，应力路径

引言

区别于混凝土以及金属等人造材料，岩土材料等天然材料具有更为明显的弱凝聚力现象.这来源于土的三个基本特性，即摩擦性、压硬性和剪胀性.摩擦性实际上表明了岩土材料的破坏性质，说明其破坏主要是由应力比来控制;而压硬性则描述岩土材料模量的变化特点;剪胀性则说明其实质是压剪耦合材料，表述的是硬化屈服阶段下的变形特点.对于土的力学特性认识也始于其强度理论的建立.库伦创立了库伦定律，用剪切面法向应力的函数,描述了二维应力条件下砂土剪切强度.此后，随着金属材料等其他材料的广泛运用，涌现出了众多的强度理论.按照所建立的模型是否具有物理涵义来区分，可分为物理模型与数学模型，前者包括摩尔--库伦强度准则[1]、SMP强度准则[23]、双剪强度准则[4]，后者包括Lade-Duncan准则[5]、Hoek-Brown准则[68].按照数学表达形式来区分，可分为线性强度准则与非线性强度准则，前者有摩尔--库伦强度准则、双剪强度准则，而后者有SMP强度准则、Lade-Duncan强度准则、Willam-Warnke准则[9]以及新近发展的S准则[10]和广义非线性强度准则[1112]等.

目前大多数的强度准则一般从几何空间中的破坏面入手来构建强度理论，如摩尔--库伦强度准则认为在二维应力空间τ-σ中存在破坏面，且破坏面上剪应力与法向应力之比为常数，是土摩擦角的正切值.由于未能考虑中间主应力的影响，当其用于三维应力状态下的破坏时，往往低估了实际材料强度值.俞茂鋐等[13]提出了双剪应力强度理论，认为作用于某一单元面上的大主剪应力与中间主剪应力的函数达到某一极限值时，材料开始发生屈服破坏，并利用强度面外凸性得到了强度理论的上限.由于未考虑静水压力的影响，材料在不同静水压力下偏平面上的破坏面形态始终不变，这不符合实际.事实上，Randolph[14]通过岩土试验发现，在较小的静水压力下,偏平面上破坏面形状为较尖锐的曲边三角形；当静水压力增大时，破坏面形状逐渐趋向于圆形的曲边多边形.这种未考虑应力诱导各向异性的强度准则有很多，比如Zienkiewicz等[15]提出的用于描述偏平面上破坏面的形状函数，其能描述岩土破坏时的应力状态，但无法准确描述屈服状态时的应力状态.Matsuoka[16]提出的SMP强度理论，基于在三维物理空间中存在一假想滑移面的思想(这一滑移面为控制岩土材料破坏的主导因素)，将摩尔--库伦的主剪应力与法向应力之比用于该滑移面上，该滑移面为两对相邻单元面的滑移面组合形式，故也被称为三维摩尔--库伦强度准则.根据SMP空间滑移面理论，其每两个相邻主应力所确定的滑移面的外法向单位向量为与材料参数无关[17]，对于广义Mises强度理论，其空间滑移面的外法向单位向量为 /3(i=1,2,3).对于广义非线性强度理论，其偏平面上表达式为上述两准则的线性插值公式，因此其滑移面也对应为上述两个法向向量的线性插值形式，含有反映拉压强度比的参数α，与材料物性有关.由Mortara[18]提出的MNLD准则在偏平面上的表达式为SMP准则与Lade-Duncan准则的幂函数插值公式，插值参数位于幂次上，造成其偏平面上的广义偏应力强度无法显示表达，且由于其屈服准则中的强度线为直线，而强度准则中表达式为幂函数曲线，两者表述不一致.近来,研究都着重于从滑移面出发，构建反映滑移面为变量的函数来实现破坏状态的描述.张连卫等[19]基于SMP准则的滑移面，将沉积面与滑移面之间夹角的线性函数表达为滑移面上摩擦角的正切值，以此反映各向异性对强度的影响.基于试验结论，当滑移面与沉积面夹角越大，则强度值越大，当两者平行时最小.罗汀等[20]认为,在三维物理空间中存在 8个滑移面，由其中一个与沉积面夹角最小的面发挥决定作用，建立了反映各向异性强度准则,可以用来描述横观各向同性土壤材料破坏特性.Gao等[21]以广义非线性准则为各向同性准则，将描述各向异性的组构张量引入其中，建立了能描述各向异性特性的广义强度准则.上述强度准则都是从破坏面出发，引入其他影响破坏面的因素，建立反映某一特性的强度准则.

假设在平面坐标系下，摩擦角为扣除截距之后的有效摩擦角.推广至三维应力情况，由3个有效滑移面可构成空间有效滑移面.根据三维空间滑移面上主剪应力比为一定值的思想，推导得到了a准则.在偏平面上，其表达式为空间有效滑移面上的主剪应力比为定值的形式，在子午面上，为考虑岩土材料的强度及屈服特性的函数.提出了基于a准则的形状函数，并建立了基于a准则的变换应力公式，变换应力法能够反映应力诱导各向异性以及避免屈服面的奇异性，相比g(θ)方法，存在明显优点.基于a准则的变换应力法可有效地用于岩土类材料的本构模型的应力一般化模拟.

1 偏平面上a强度准则公式

在平面坐标系 σ--τ中，假设存在直线型强度线，为考虑凝聚力的摩尔--库伦模型，其表达式为

当b=0时，上式表示为过原点的直线，即

表示为无凝聚力的库伦准则.而当k=0时，则

即退化为一水平直线.当b＞0时，表示一般直线.对于大于零的任意值，假定当此直线与莫尔圆相切时，切点表示破坏状态，则可由图1表示.

图1 强度线与莫尔圆外切图Fig.1 The circumscribed figur between strength line and Mohr’s circle

由图1可见，当此直线与莫尔圆相切时，切点为 p(σn0,τn0)，根据外切条件，则有共点的条件.令强度曲线为 τ1=kσ+b，而莫尔圆函数为 τ2=[R2-(σ-σ0)2]0.5.其中，R表示莫尔圆的半径，而σ0则表示为莫尔圆的圆心横坐标值.由上述两条件，可得如下方程

由式(5)可知为关于应力σ的一元二次方程，根据两函数相切的条件可知解是唯一的，因此可得到关于方程式(5)的根的判别式Δ=0，显然上述判别方程是关于参数k的一元二次方程，再利用求根公式以及k＞0的条件，通过求解可得到

记此时的切线斜率为等效摩擦角的正切值

其中，φe表示有效内摩擦角

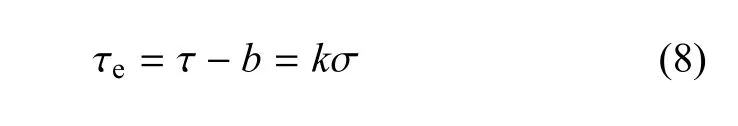
任意一条切线可表示为剪应力与正应力之比的形式.由图1可见，b的最大值为R，因此可令

其中，参数a介于0～1之间，是控制偏平面上强度线形状的参数.

图2中φe13表示由第一、第三主应力所构成的有效摩擦角，余下表示同理.由图2所示，对于三轴压缩，在由σ1,σ3组成的一对应力作用下，滑移面与σ1作用面所成的夹角为45◦+φe13/2.其中，φe13为直线型强度线与莫尔圆的切点所对应的等效摩擦角.根据SMP空间滑移面的构建思路，在三维物理空间中也相应存在一个等效滑移面(图3)，其上为等效剪应力τen和等效正应力σen.下面推导该等效剪应力以及等效正应力.

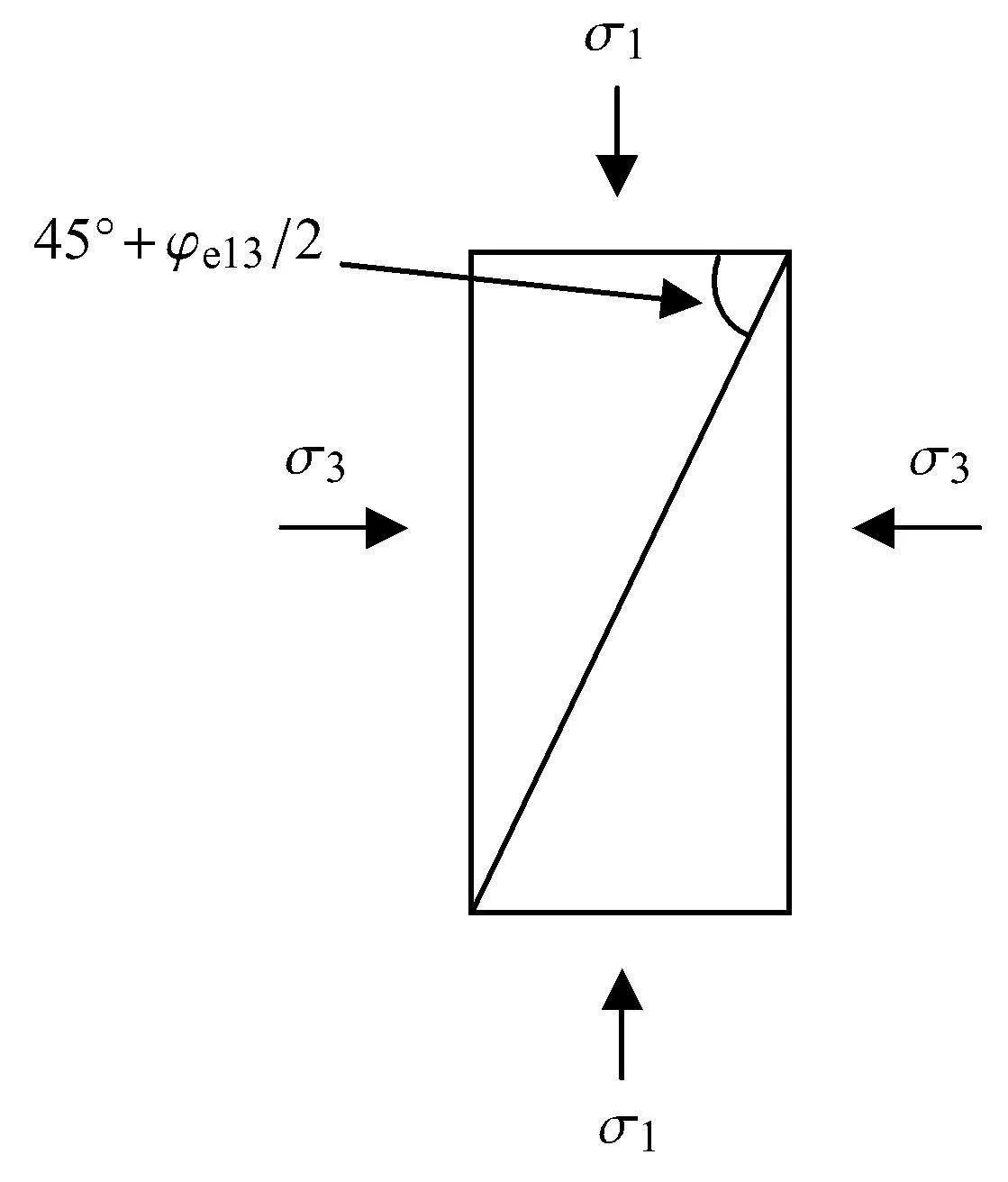
图2 三轴试样中的滑移面Fig.2 The slip plane in a sample for triaxial test

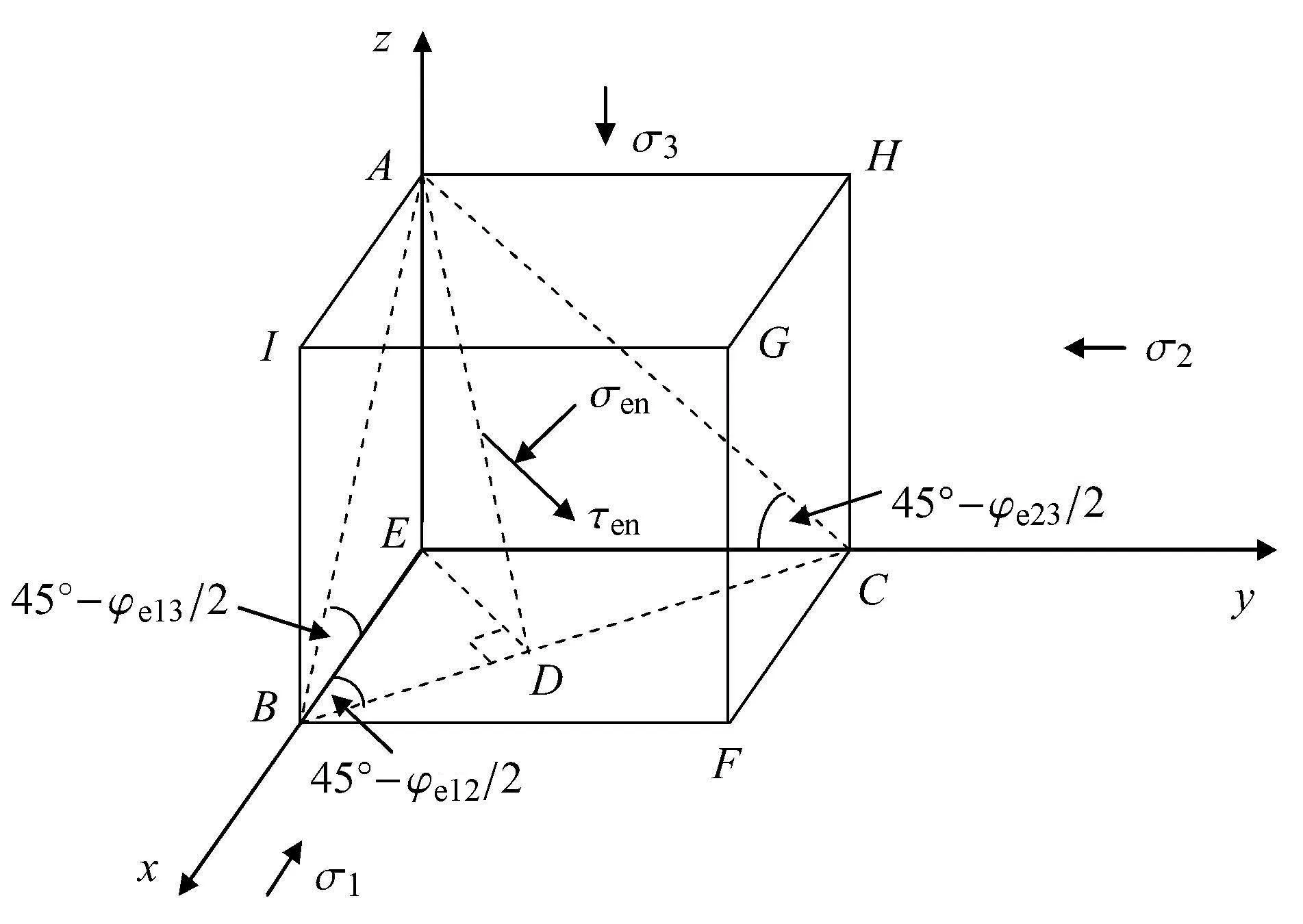
图3 空间坐标系中的滑移面Fig.3 The slip plane in three dimensional space coordinate

令EA=1，根据三角函数关系，线段AB与BE形成的夹角为45◦-φe13/2，在直角三角形AEB中，根据三角函数关系可得

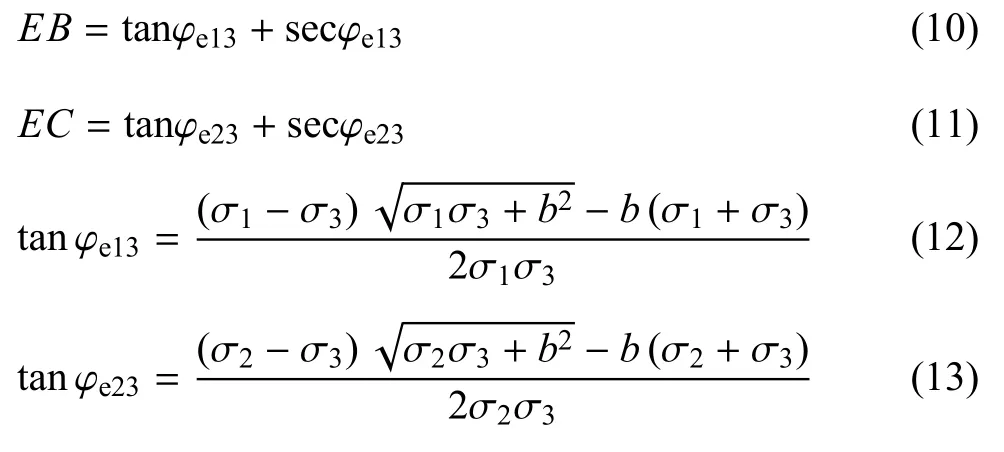
对于四面体ABCE，可先确定其斜面的法向，由余弦确定.则该斜面上法向方向线与 3个坐标轴之间夹角的余弦分别表示为 l,m,n. 令 r=

根据正四面体AEBC的力平衡关系，利用上述公式，可得到等效正应力公式

其中，σen,τen分别为三维滑移面上的等效正应力及等效剪应力.推导可得到

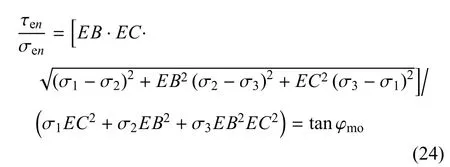
其中，φmo为三维空间中有效滑移面的摩擦角.当反映凝聚力的参数a变化时，可得到如下两种强度准则.

(1)当a=0时，函数退化为过原点的斜线，则此时根据莫尔圆上的几何关系，可得

根据四面体ABCE的力平衡条件，可推导得到

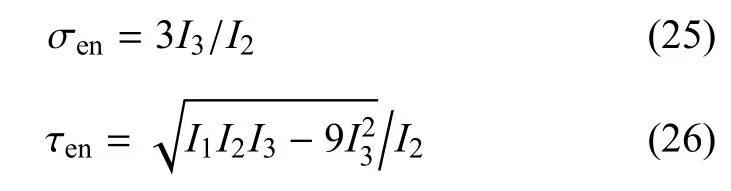
其中，I1,I2,I3分别为主应力的第一、第二、第三应力不变量，因此，正应力与剪应力均退化为SMP面上的正应力与剪应力.

(2)当a=1时，函数退化为与横坐标轴平行的水平直线.四面体上斜面退化为八面体面，根据对称性，该面上法线余弦相√等，且由其平方和为1的条件，可知l=m=n=/3，因此得到

其中，p为有效球应力，q为有效广义偏应力.

当处于三轴压缩时，式(24)可表达为

此时，大小主应力分别可表示为

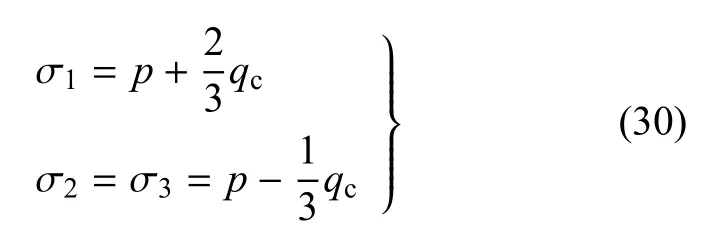
其中，qc为三轴压缩破坏时的有效广义偏应力.将式(30)代入式(24)中，可得到关于p,qc的函数

其中，采用破坏时应力比的表示方法，M=qc/p,则过程变量可表示为

其中，M表示三轴压缩时的破坏应力比.设三轴拉伸破坏应力比为Me，三轴拉伸破坏应力比与三轴压缩破坏应力比之比值为β，则Me=βM.

由于在三轴压缩路径下，方程式(24)与式(31)完全相等，因此得到

式(37)为广义偏应力强度公式.

2 子午面上a强度与屈服准则公式

在子午面上，岩土具有典型的摩擦性和压剪耦合特性，偏应力增大不仅导致剪切屈服，也会产生一定程度的体积压缩屈服.纯静水压力的增减不仅直接导致体积屈服同时也会引发剪切屈服，屈服准则表达式中暗含的剪切强度线与破坏准则表达式中的剪切强度线一致.为能统一描述子午面上剪切强度以及压剪耦合屈服特性，可采用开关函数来表达该准则.

子午面上的广义偏应力qc可以表示为如下统一的表达式

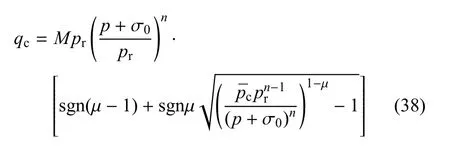
其中，σ0表示三向拉伸强度,pr为参考球应力.反映在此应力值下子午面上破坏曲线的割线斜率,可保证式(38)括号中的比值量纲唯一，使等式左右量纲相同.对于散粒体材料，pr通常取标准大气压值.µ为反映压剪耦合特性的材料参数，由岩土的不排水剪切强度来确定，参数n为子午面上强度曲线的幂次函数,M表示岩土破坏时应力比参数.¯pc表示屈服面在-面上与轴的右端交点，为状态参数，表征加载过程中屈服面的硬化程度，称为硬化应力.

开关函数为

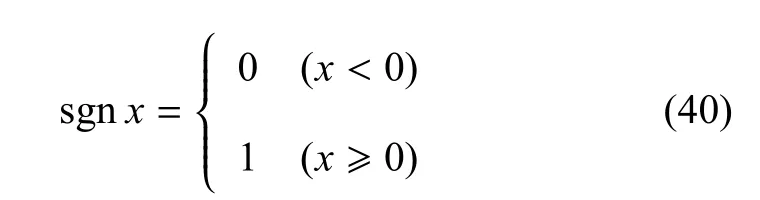
当µ=1时，则式(38)退化为

当0≤µ＜1时，则式(38)退化为

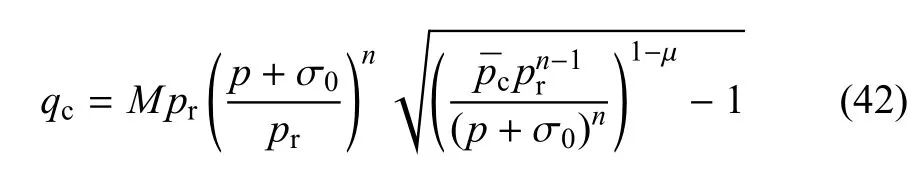
当µ=1时，a准则在主应力空间为开口曲面，描述的是岩土在剪切破坏模式下的特性，其破坏曲面如图4所示.而当0≤µ＜1时，则a准则表述的是岩土剪切、等向压缩耦合特性的屈服面.图4所示为a准则所描述的岩土在主应力空间中的破坏面.

图4 主应力空间中的破坏面Fig.4 The failure surface in principal stress space

3 a强度与屈服准则参数

3.1 参数a的涵义及确定

由于参数a介于0与1之间，反映的是材料凝聚性与摩擦性对材料破坏贡献的权重，具体反映在偏平面上破坏面的形状变化，金属属于典型的凝聚型材料，砂土等散体属于典型的摩擦性材料.这两种材料的偏平面破坏形状分别为圆形和曲边三角形，三轴拉伸偏应力剪切强度对应的是最小半径，即三轴拉伸应力路径所对应的剪切强度值是所有应力路径中最小的.因此可利用三轴拉伸强度与三轴压缩强度之比β表示材料参数a，建立两者的直接函数关系，即可简单地利用三轴拉伸与三轴压缩两种应力路径下的试验结果来确定参数a.根据a强度准则表达式(24)，可得到三轴拉伸应力路径下的方程.

在三轴拉伸路径下，有如下关系

其中,qe为三轴拉伸破坏时的有效广义偏应力.将式(43)代入式(10)中，且Me=qe/p=βM，则可得到

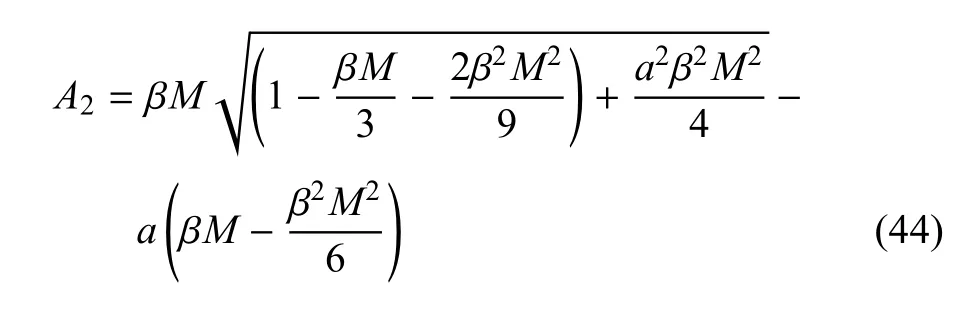
采用三轴拉伸与压缩应力比β可进一步化简为

将式(43)～式(47)代入式(24)，由于式(24)与式(31)相等，可得

式(48)是隐函数，无法直接解出关于变量β的a函数.如图5所示，可采用较为简单的函数来代替上述隐函数关系.形状参数a与三轴拉伸压缩强度比β之间的关系见图5中的虚线，考虑到两者之间为隐函数关系且形式较为复杂，采用简单的抛物线函数来描述两者的关系，其关系表达式为

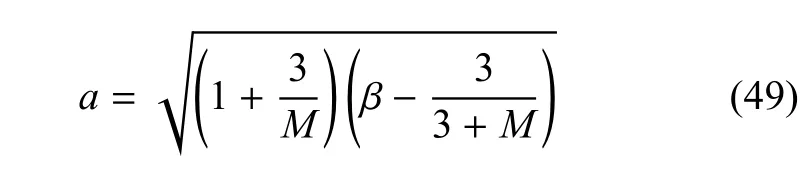
图5 采用抛物线代替形状函数的比较图Fig.5 Comparison between parabola with shape function

3.2 参数µ的涵义及确定

压剪耦合参数µ是反映岩土剪切压缩与体积压缩相互耦合程度的土性参量.可由三轴压缩不排水应力路径下固结不排水抗剪强度来确定.根据屈服面的解析式(42)，可由体变为零条件导出如下公式来确定参数µ

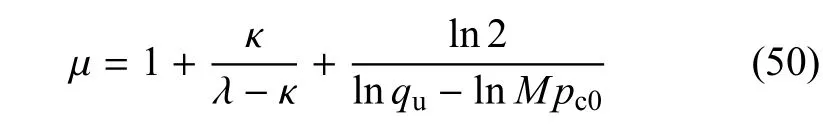
其中，λ，κ分别为在e-lnp空间中整理得到的压缩斜率与回弹斜率；e0为土体的初始孔隙比.在不排水条件下当土体处于临界状态时，应力比达到破坏应力比M，此时的剪应力为不排水抗剪强度qu，pc0为初始固结应力.

参数µ对子午面上屈服面形状的影响如图6所示.当µ=1时，屈服曲线与 p轴相重合.当µ=0时，屈服面为图中最高偏应力值最大的封闭曲线，与之相对应的应力比强度线M为曲线，并通过屈服面最高点.

图6 参数µ对屈服曲线形状的影响Fig.6 Influenc of parameterµon the shape of yield surface

3.3 参数n的涵义及确定

参数n为子午面上强度曲线的幂次，表示子午面上破坏曲线的弯曲程度.如图7所示，当n=0时，曲线退化为与静水压力无关的直线，与静水压力轴平行.当n=1时，幂函数曲线退化为一条斜线.当0＜n＜1时，幂函数曲线退化为介于上述两条直线之间的开口曲线.通过式(41)变形可得到如下的关系式

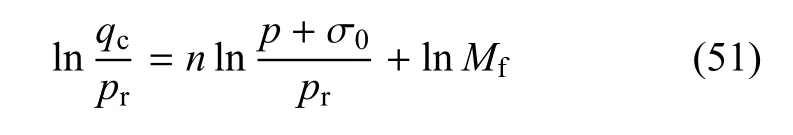
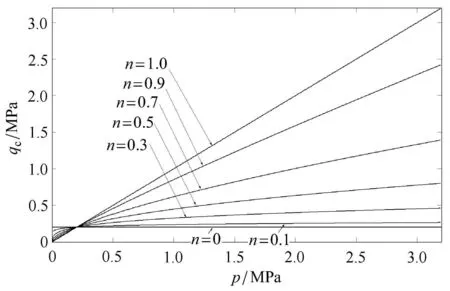
图7 子午面上幂参数n对破坏曲线形状的影响Fig.7 Influenc of parameter n on meridian plane on the shape of failure surface

以等式左右两端的对数分别为变量，式(51)是关于参数n的一次函数，利用三轴压缩试验结果，可将不同静水压力下的剪切强度整理在对数坐标系内，拟合出的直线，斜率为n，而截距为ln Mf.

3.4 参数σ0的涵义及确定

σ0为强度曲线与静水压力轴的左交点值，其物理意义为材料在拉伸条件下的强度，可反映材料的凝聚力.图8所示为σ0对破坏曲线形状的影响.事实上，材料在三向拉伸作用下的强度值，一般很难获得，对于无黏性土，取为0.对于具有拉伸强度的材料，如混凝土等，可将其取为单轴拉伸强度值的0.9倍.

图8 子午面上幂参数σ0对破坏曲线形状的影响Fig.8 Influenc of parameter σ0on meridian plane on the shape of failure surface

3.5 参数pr的涵义及确定

参数pr反映在一定静水压力下，将剪切强度q归一化的特征压力，也起将静水压力无量纲化的作用.对于砂土等散粒体材料，通常取一个大气压.由图9可见，当pr逐渐增大时，剪切强度初始斜率增大，且整体剪切强度增大.参数pr可根据式(51)，将试验结果整理在对数坐标系内，根据拟合直线来确定.

4 a强度与屈服准则特性

考察a准则中强度与参数a的影响，由图10可见，当固定强度应力比参数β时，参数a与三轴压缩应力比强度值M之间呈抛物线关系，且随着参数β的增大，曲线逐渐左移，向坐标原点靠近，当β=1时，曲线与纵坐标轴重合，a是M的常数型函数，不随M的变化而变化，值恒定为1.

图9 子午面上幂参数pr对破坏曲线形状的影响Fig.9 Influenc of parameter pron meridian plane on the shape of failure surface

图10 抛物线中随强度应力比的变化a与M的关系Fig.10 Relationship between a and M in parabola with change of stress ratio

图11显示的是参数a的变化对偏平面上强度曲线的影响.从图11可以看出：当a=0时，强度准则退化为SMP强度准则；当a=1时，强度准则退化为Mises强度准则；当0＜a＜1时，截面形状介于两者之间.说明所提a准则能包含或者接近现有常见的准则，当0＜a＜1时，接近于Lade-Duncan准则.当参数a逐渐增大时，曲线形态由曲边三角形逐渐向圆形过渡，其对应的应力罗德角对强度的影响逐渐削弱，当退化为Mises准则时，应力罗德角对最终强度值无影响.所提a准则具有很强的物理意义，反映的是材料由摩擦性逐渐向凝聚性过渡，以应力比为控制因素向偏应力破坏因素转移，而处于中间状态的准则则是介于两者之间的情形.

当固定其他参数时，考察应力比强度对偏平面上强度曲线的影响如图12所示.从图12可以看出：当Mf=0时，强度曲线退化为与偏平面的法线，即主应力空间中的等倾线，与p轴相重合；当应力比强度增大，对应的偏平面上广义偏应力强度逐渐增大；同时，应力比强度对强度曲线偏平面形状具有显著影响；当应力比强度值较小时，偏平面上强度曲线接近于圆形；当应力比强度逐渐增大时，强度曲线趋近于曲边三角形，各向异性显著增强.

图11 参数a对破坏曲线形状的影响Fig.11 Influenc of parameter a on the shape of failure surface

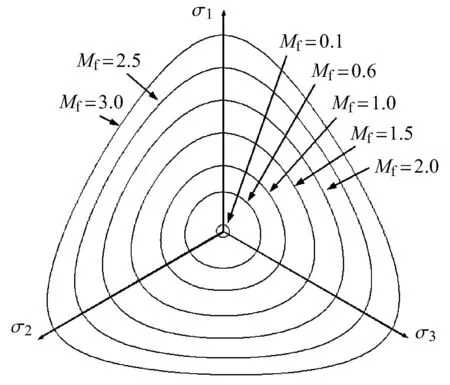
图12 参数Mf对破坏曲线形状的影响Fig.12 Influenc of parameter Mfon the shape of failure surface

考察静水压力p(p=3I1)对强度曲线的影响，图13所示为当I1=100，200，400，600，800，1000，1200kPa时的偏平面强度曲线，随静水压力p增大，广义偏应力强度逐渐增大，强度曲线形状也由曲边三角形逐渐向圆形发展，材料趋于各向同性.所提的a准则能反映静水压力对强度非线性影响，也能反映静水压力对材料各向异性的影响.

静水压力不仅对岩土的强度特性产生影响，对其屈服特性也会产生影响.图14所示为不同静水压力下的偏平面上的屈服特性曲线.球应力为100,200,400，600，800，1000，1200kPa时所对应的屈服曲线包围的面积由外向内依次减小.随着球应力的增大，广义偏应力逐渐减小，并最终趋于p轴的一点.此外，屈服曲线形状也由比较尖锐的曲边三角形趋向为近似圆形，应力罗德角与屈服面轨迹的差异性减弱，表明球应力的增大减弱了各向异性.

图13 静水压力对破坏曲线形状的影响Fig.13 Influenc of hydrostatic pressure on the shape of failure surface

图14 静水压力对屈服曲线形状的影响Fig.14 Influenc of hydrostatic pressure on the shape of yield surface

5 基于a强度准则的一般化应力变换公式

材料参数a影响偏平面上强度曲线的形状(图11)，且都通过三轴压缩路径上一点.根据变换应力一般化的思路，可采用图11中强度曲线上任意一点的应力状态来表示三轴压缩上的应力状态.在三轴压缩路径下，材料达到强度线上的应力状态时，根据空间滑移面的物理意义，三轴压缩路径下与一般应力路径下的空间滑移面上的剪应力与正应力之比相等.

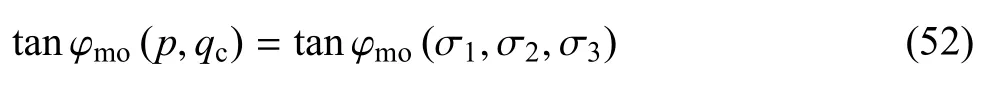
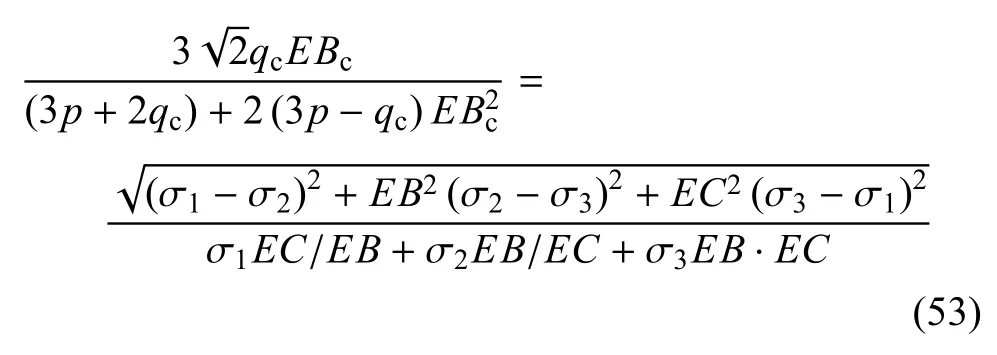
类比SMP的形状函数[22]，a准则表达式也具有更为一般的摩擦法则涵义，因此，其表达式的广义偏应力可表示为

其中，EB,EC是σ1,σ2,σ3的函数，具体见式(10)～式(13)

其中，θ为应力罗德角，可表示为

对应a准则的偏平面上的形状函数可表示为

由于已知有基于a准则的形状函数，因此，可得到在任意一个球应力p下的三轴压缩路径下的广义偏应力qc

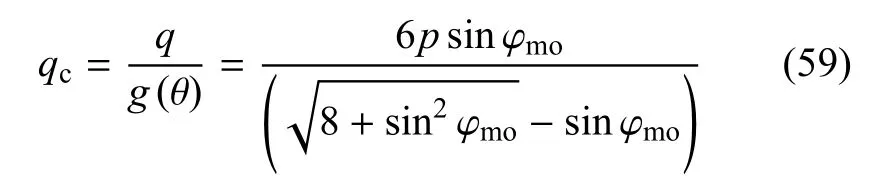
由于变换应力是基于每个增量步进行变换，对于当前应力，将其用偏应力分量si来表示，由于在偏平面上偏应力为主要考察因素，因此将每一应力的偏应力分量与三轴压缩路径下的偏应力分量做对比，可对每个应力的所有分量成比例放大成与qc相对应的相同值，因此可参考Yao等[23]基于SMP准则的变换应力方法，采用的基于a准则的一般化变换应力公式可表示为

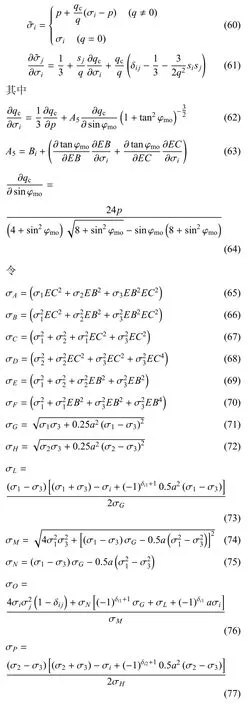
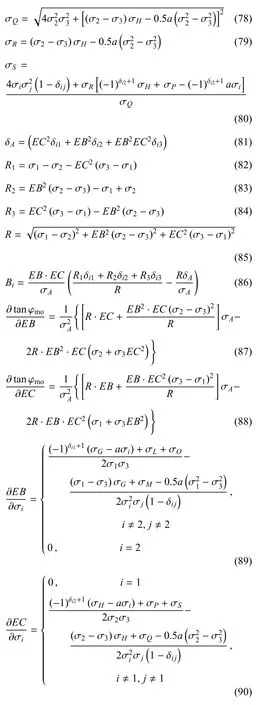
式(55)～式(60)为将普通应力转换为变换应力空间的变换应力公式，而式(61)～式(90)为将变换应力空间中变换应力应用到具体本构模型中时微分的导函数公式.在将p,q变量转换为三维应力一般化方法中，g(θ)是应用较为广泛的一种，然而该方法仅仅是将强度线利用形状函数法表示出来，而形状函数法所表示的强度线在偏平面上不随静水压力变化而发生改变，无法反映岩土的应力诱导各向异性.而采用所提的变换应力法由于实质上在每一增量步都采用随当前应力产生改变的屈服面，因而能够避免上述缺陷.

6 强度及屈服准则预测及变换应力法验证

选用一系列岩土的测试结果对a强度与屈服准则以及变换应力公式进行检验，以验证a准则的正确性及适用性.岩土参数见表1.

表1 岩土参数Table 1 Geomaterial parameters

6.1 强度准则预测

采用多种不同岩土对a强度准则进行验证.

主应力空间中偏平面上丰浦砂真三轴试验[24]与预测结果对比如图15所示，图中圆圈点为196kPa时有效球应力的试验结果，此时应力罗德角分别为0◦，15◦，30◦，45◦，60◦，预测曲线为图 15中实线.从图15可以看出，a准则较好地描述了砂土在真三轴路径下的强度特性.

主应力空间中偏平面上混凝土真三轴试验[25]与预测结果对比如图16所示，图中的方格点为其破坏点，从内到外依次对应的是I1=1,2,3,4,5,6,7MPa时的破坏点轨迹.图中实线为在上述静水压力下的预测结果.在较低静水压力(1MPa)下，过低地估计了三轴压缩下的剪切强度，而在静水压力为7MPa时则过高地估计抗剪强度.而介于两者之间的则吻合较好.

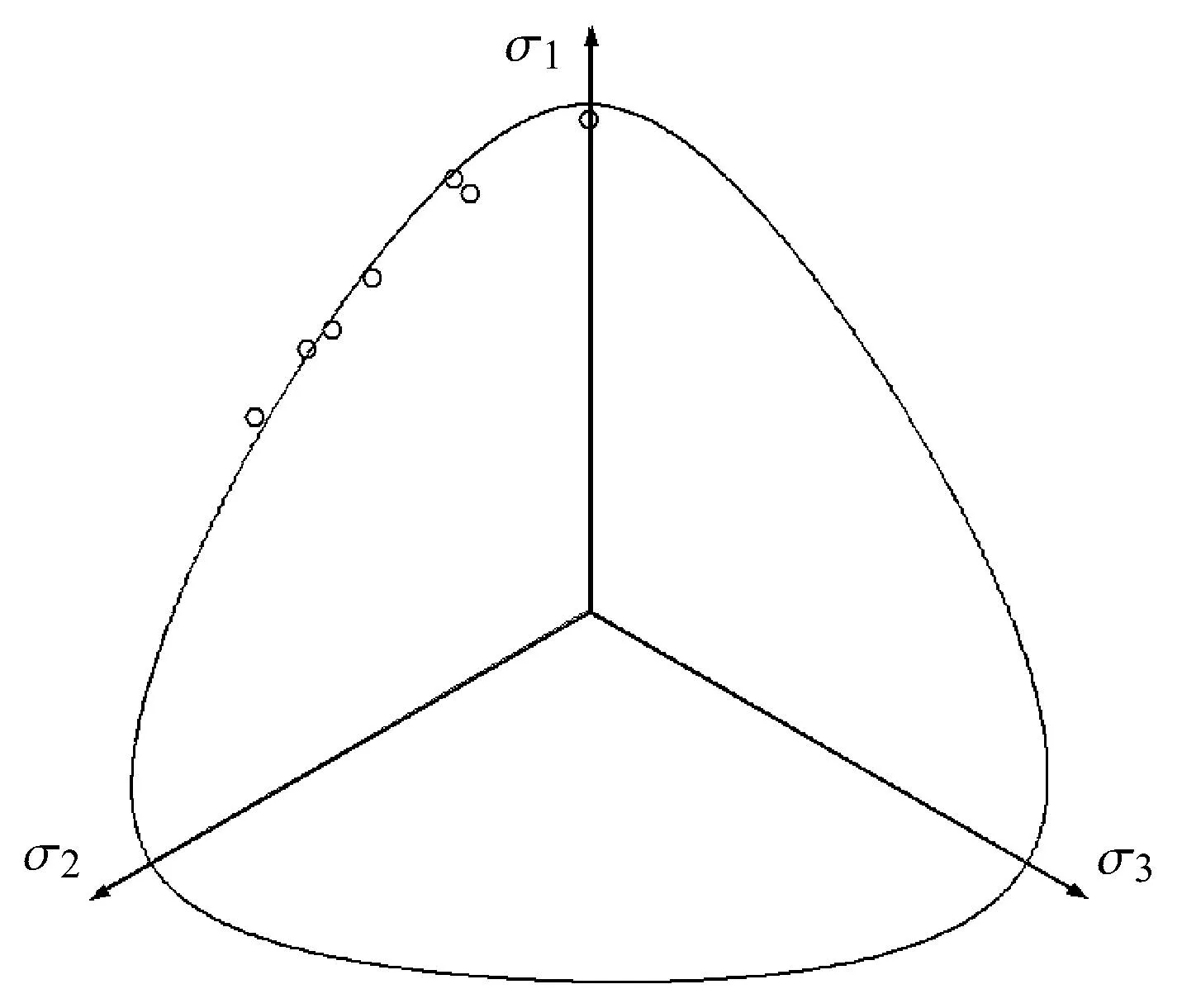
图15 主应力空间中偏平面上丰浦砂真三轴试验[24]与预测对比Fig.15 Comparison between test[24]and prediction results for Toyoura sand on deviatoric plane in principal stress space

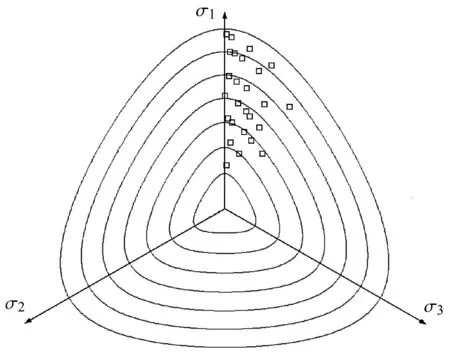
图16 主应力空间中偏平面上混凝土真三轴试验[25]与预测结果对比Fig.16 Comparison between true triaxial test[25]and prediction results for concrete on deviatoric plane in principal stress space

图17所示为子午面上混凝土三轴压缩及三轴拉伸路径下试验与预测结果[2628]，其中 fc为混凝土的单轴抗压强度(4MPa).从图17可以看出，在较低静水压力下，三轴压缩以及三轴拉伸路径所得到的测试点归一性较好；当静水压力较大时出现了较大的离散性.图中实线和虚线分别表示对三轴压缩以及三轴拉伸路径下的强度预测结果.对比可见，所提a强度准则可对混凝土在这两种应力路径下强度特性进行合理的描述.

图18中试验点为中科院武汉岩土所对花岗岩开展的真三轴试验测试结果[29]，图中实线由内到外依次对应的是静水压力p=80，110，130，155，195kPa时的预测结果.由对比可见，在偏平面上，所提的a准则在不同静水压力下可以有效地用于花岗岩的强度特性描述.

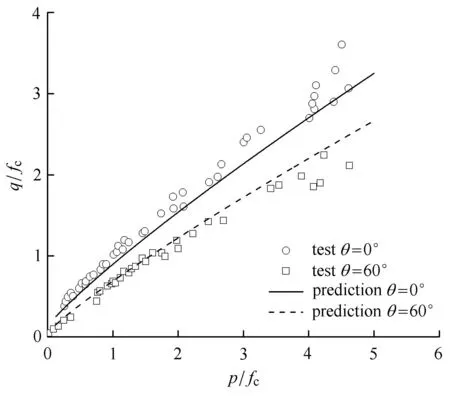
图17 子午面上混凝土三轴压缩及三轴拉伸路径下试验[2628]与预测结果对比Fig.17 Comparison between test[2628]and prediction results for concrete under triaxial compression and extension conditions on meridian plane

图18 偏平面上花岗岩真三轴应力路径下试验[29]与预测对比Fig.18 Comparison between true triaxial test[29]and prediction results for grunite on deviatoric plane

由图19可见，在子午面上显示的是对应不同应力罗德角下的强度预测对比.在应力罗德角较大(θ=60◦)时，预测抗剪强度值偏低；而当应力罗德角逐渐减小到0◦时，抗剪强度逐渐增大.这符合偏平面上的曲边三角形特点.而在试验结果中，当静水压力较大时，对应θ=13.9◦时的强度值比三轴压缩稍大，这可能源于花岗岩本身具有的原生各向异性，岩石内部存在裂隙面，因而会对加载结果产生影响.

图19 子午面上花岗岩真三轴应力路径下试验与预测结果对比Fig.19 Comparison between true triaxial test and prediction results for grunite on meridian plane

6.2 屈服特性准则预测

黏土具有典型的压剪耦合特性，研究其硬化过程的主要对象是其体积屈服规律.王靖涛等[30]曾针对黏土开展了等塑性体应变的屈服轨迹试验，试验结果如图20所示，见图中等向压缩路径下固结压力为128～354kPa时对应的等塑性体应变的屈服点.由图20可见，采用考虑压剪耦合特性的屈服准则可有效地用于预测黏土的屈服轨迹.

图20 子午面上黏土体积屈服特性试验[30]与预测结果对比Fig.20 Comparison between test[30]and prediction results of volume yield behavior for clay on meridian plane

图21中试验点为黄文熙等[31]针对承德砂土开展的等塑性体应变的屈服轨迹试验.由预测对比可见，所提的屈服准则也可较好地描述砂土的体积屈服轨迹.

图21 子午面上砂土体积屈服特性试验[31]与预测结果对比Fig.21 Comparison between test[31]and prediction results of volume yield behavior for sand on meridian plane

6.3 变换应力法验证

Lade等[32]针对grunnite黏土进行了真三轴应力路径试验，试验约束条件是不排水，中主应力系数b=0，0.21，0.4，0.7，0.95.初始固结压力为147kPa.采用DUH模型[33]对上述应力路径进行模拟，所得对比结果如图22～图25所示.其中，图22为大小主应力比与大主应变的关系对比.从图22可以看出，采用所提准则进行应力一般化后的修正DUH模型可较好地描述真三轴应力路径下黏土的应力应变关系特性.图23为相应的孔压固结压力比与大主应变的关系对比，当b值较大时，预测的孔压稍大.图24和图25分别为对应的中间主应变与小主应变与大主应变的关系，由图可见，除了b=0.21时对应的应力路径偏差稍大外，其余预测结果与试验结果吻合较好.

图22 应力比与大主应变关系试验[32]与预测结果对比Fig.22 Comparison between test[32]and prediction results of stress ratio and principal strain for grunnite clay

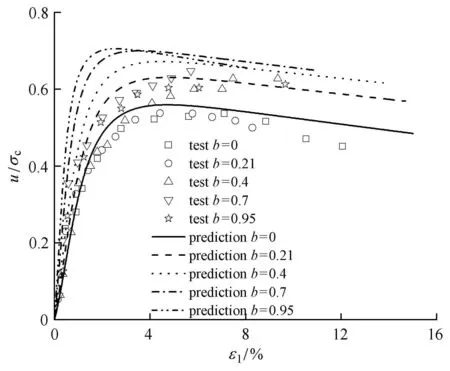
图23 孔压特性试验[32]与预测结果对比Fig.23 Comparison between test[32]and prediction results of pore water pressure behavior for grunnite clay

图24 大主应变与中间主应变关系试验[32]与预测结果对比Fig.24 Comparison between test[32]and prediction results of principal strain and middle principal strain for grunnite clay

图25 大主应变与小主应变关系试验[32]与预测结果对比Fig.25 Comparison between test[32]and prediction results of principal strain and small principal strain for grunnite clay

图26所示为Dakoulas等[34]关于Ottawa松砂的三种应力路径试验结果，分别对应b=0，0.5，1.球应力为300kPa时的真三轴应力路径.大小主应力差半值与轴应变以及八面体偏应变的结果对比较好，八面体偏应变对应的是b=0.5应力路径.由对比可见，采用所提变换应力法修正后的DUH模型也可用于砂土的真三轴的应力--应变关系模拟.

图26 应力差与轴应变关系试验[34]与预测结果对比Fig.26 Comparison between test and prediction results of relationship between di ff erential stress and axial strain for grunnite clay

7 结论

通过假定三维空间中存在一有效滑移面，且滑移面上的主剪应力比为定值，建立了三维空间中的破坏准则，在子午面上强度曲线族可由幂函数来表示，针对岩土的压剪耦合特性引入了屈服准则表达式.基于a强度准则建立了从二维到三维模型的变换应力公式.所提a强度与屈服准则及其变换应力公式具有如下特点.

(1)所建立的 a强度准则，由于引入了可以考虑黏聚性以及摩擦性两者对于破坏贡献的权重系数a，因而其强度上限为广义Mises强度准则，其强度下限为SMP强度准则.通过改变系数a，可得到介于上述两者之间的任一强度线，该准则可用于预测土壤、混凝土、岩石等工程材料的破坏行为.

(2)基于a强度准则所提出的屈服准则，由于考虑了岩土在剪切过程中偏应力对于剪应变、体应变的影响，等向压缩过程中球应力对于剪应变、体应变的交叉耦合影响，因而能够反映黏土以及砂土等材料的压剪耦合屈服特性.

(3)基于a准则所提的变换应力公式可以方便地将传统二维本构模型方便地转换为三维模型，且由于在转换过程中完全采用了a屈服准则，因而可以反映静水压力变化对于屈服面形状变化的影响，完全避免了屈服面的应力点奇异性以及屈服面非外凸等问题.

对比砂土、黏土、混凝土、花岗岩等材料的试验结果与预测值，证明所提a强度与屈服准则以及变换应力公式可简单、明确地运用到传统模型中，具有较强的适用性.

1 Matsuoka H,Nakai T.Relationship among Tresca,Mises,Mohr Coulomb and Matsuoka-Naka failure criteria.Soil sand Foundatiens,1985,25(4)：123-128

2 Nakai T,Matsuoka H.Shear behaviors of sand and clay under threedimensional stress condition.Soils and Foundations,1983,23(2)：26-42

3 Matsuoka H.On the significanc ofthe spatial mobilized plane.Soil and Foundations,1976,16(1)：91-100

4俞茂鋐.岩土类材料的统一强度理论及其应用.岩土工程学报,1994,16(2)：1-10(Yu Maohong.Unifie strength theory for geomaterials and its applications.Chinese Journal of Geotechnical Engineering,1994,16(2)：1-10(in Chinese))

5 LadePV,DuncanJM.Elastoplasticstress-straintheoryforcohesionless soil.Journal of Geotechnical and Geoenvironmental Engineering Division,1975,101(1)：1037-1053

6 Hoek E,Brown ET.Practical estimates of rock mass strength.International Journal of Rock Mechanics and Mining Sciences,1997,34(8)：1165-1186

7姜华.一种简便的岩石三维Hoek-Brown强度准则.岩石力学与工程学报,2015,34(S1)：2996-3004(Jiang Hua.A simple convenient three-dimnesional Hoek-Brown criterion for rocks.Chinese Journal of Rock Mechanics and Engineering,2015,34(S1)：2996-3004(in Chinese))

8昝月稳,俞茂宏.岩石广义非线性统一强度理论.西南交通大学学报,2013,48(4)：616-624(Zan Yuewen,Yu Maohong.Generalized nonlinear unifie strength theory of rock.Journal of Southwest Jiaotong University,2013,48(4)：616-624(in Chinese))

9王怀亮,宋玉普.多轴应力状态下混凝土的动态强度准则.哈尔滨工业大学学报,2014,46(4)：93-97(Wang Huailiang,Song Yupu.A dynamic strength criterion of concrete under multiaxial stress state.Journal of Harbin Institute of Technology,2014,46(4)：93-97(in Chinese))

10王国盛,路德春,杜修力等.基于S准则发展的混凝土动态多轴强度准则.力学学报,2016，48(3)：636-653(Wang Guosheng,Lu Dechun,Du Xiuli,et al.Dynamic multiaxial strength criterion for concretedevelopedbasedontheScriterion.ChineseJournalofTheoretical and Applied Mechanics,2016,48(3)：636-653(in Chinese))

11姚仰平,路德春,周安楠等.广义非线性强度理论及其变换应力空间.中国科学E辑,2004,34(11)：1283-1299(Yao Yangping,Lu Dechun,Zhou Annan,et al.Generalized non-linear strength theory and transformed stress space.Science China Technological Sci-ences,2004,47(6)：691-709(in Chinese))

12万征,姚仰平.考虑压剪耦合特性的岩土材料广义非线性屈服准则.岩石力学与工程学报,2014,33(2)：376-389(Wan Zheng,YaoYangping.A new generalized nonlinear yield criterion for geomaterials considering coupling behavior or shearing and compression.Chinese Journal of Rock Mechanics and Engineering,2014,33(2)：376-389(in Chinese))

13俞茂宏,何丽南,宋凌宇.广义双剪应力强度理论及其推广.中国科学A辑,1985,28(10)：1113-1121(Yu Maohong,He Linan,Song Lingyu.Twin shear stress theory and its generalization.Science in China,Series A,1985,28(10)：1174-1183(in Chinese))

14 Randolph H.Generalising the Cam-clay models//Proceedings of Symposium on the Implementation of Critical State Soil Mechanics in FE Computations.Cambridge：Cambridge University Press,1982：1-5

15 Zienkiewicz OC,Pande GN.Some useful forms of isotropic yieldsurface for soil and rock mechanics//Pande GW.Finite Elements in Geomechnaics.London：Wiley,1977：179-190

16 Matsuoka H.On the significanc of the “spatialmobilized plane”.Soils and Foundations,1976,16(1)：91-100

17杜修力,马超,路德春.岩土材料的非线性统一强度模型.力学学报,2014,46(3)：389-397(Du Xiuli,Ma Chao,Lu Dechun.Nonlinear unifie strength model of geomaterials.Chinese Journal of Theoretical and Applied Mechanics,2014,46(3)：389-397(in Chinese))

18 Mortara G.A new yield and failure criterion for geomaterials.Geotechnique,2008,58(2)：125-132

19张连卫,张建民,张嘎.基于SMP的粒状材料各向异性强度准则.岩土工程学报,2008,30(8)：1107-1111(Zhang Lianwei,Zhang Jianmin,ZhangGa.SMP-basedanisotropicstrengthcriteriaofgranular materials.Chinese Journal of Geotechnical Engineering,2008,30(8)：1107-1111(in Chinese))

20罗汀,李萌,孔玉侠等.基于SMP的岩土各向异性强度准则.岩土力学,2009,30(S2)：127-131(Luo Ting,Li Meng,Kong Yuxia,et al.Failure criterion based on SMP for anisotropic geomaterials.Rock and Soil Mechanics,2009,30(S2)：127-131(in Chinese))

21 Gao ZW,Zhao JD,Yao YP.A generalized anisotropic failure criterion for geomaterials.International Journal of Solids and Structures,2010,47(22-23)：3166-3185

22 Matsuoka H,Yao YP,Sun DA.The Cam-clay models revised by the SMP criterion.Soils and Foundations,1999,39(1)：81-95

23 Yao YP,Wang ND.Transformed stress method for generalizing soil constitutive models.Journal of Engineering Mechanics,2014,140(3)：614-629

24 Nakai T,Matsuoka H.Shear behaviors of sand and clay under threedimensional stress condition.Soils and Foundations,1983,23(2)：26-42

25 Launay P,Gachon H.Strain and ultimate strength of concrete under triaxial stresses.Revista Brasileira De Educac¨ao,1970,11(32)：340-345

26 Ottosen NS,A failure criterion for concrete.Journal of Engineering Mechanics,1977,103(4)：527-535

27 Mills LL,Zimmerman RM.Compressive strength of plain concrete under multiaxial loading conditions.Journal of the American Concrete Institute,1970,66

28 Cedolin L,Crutzen YRJ,Poli SD.Triaxial stress-strain relationship for concrete.Journal of Engineering Mechanics,1977,103(3)：423-439

29李小春，许东俊，刘世煜等.真三轴应力状态下拉西瓦花岗岩的强度、变形及破裂特性试验研究//中国岩石力学与工程学会编.中国岩石力学与工程学会第三次大会论文集,北京,1994.北京：中国科学技术出版社,1994：153-159(Li Xiaochun,Xu Dongjun,Liu Shiyu et al.The experimental research of the strength,deformation and failure properties of Laxiwa granite under the status of true triaxial stresses//Chinese Society of Rock Mechanics and Engineering eds.Proceedings of the Third Conference of Chinese Society of Rock Mechanics and Engineering.Beijing,1994.Beijing：China Science and Technology Press,1994：153-159(in Chinese))

30王靖涛，李国成.岩土材料屈服轨迹的弯曲及相关问题.华中科技大学学报(自然科学版),2015,43(10)：92-95(Wang Jingtao,Li Guocheng.Yielding loci curving and related problems of geotechnical materials.Journal of Huazhong University of Science and Technology(Nature Science Edition),2015,43(10)：92-95(in Chinese))

31黄文熙,濮家骝,陈愈炯.土的硬化规律和屈服函数.岩土工程学报,1981,3(3)：19-26(Huang Wenxi,Pu Jialiu,Chen Yujong.Hardening rule and yield function for soils.Chinese Journal of Geotechnical Engineering,1981,3(3)：19-26(in Chinese))

32 Lade PV,Musante HM.Three-dimensional behavior of remolded clay.Journal of Geotechnical and Geoenvironmental Engineering Division,1978,104(2)：193-209

33 Wan Z.A cyclic UH model for sand.Earthquake Engineering and Engineering Vibration,2015,14(2)：229-238

34 Dakoulas P,Sun Y.Fine Ottawa sand：Experimental behavior and theoretica predictions.Journal of Geotechnical and Geoenvironmental Engineering,1992,118(10)：1906-1923

A KIND OF STRENGTH AND YIELD CRITERION FOR GEOMATERIALS AND ITS TRANSFORMATION STRESS METHOD1)

Wan Zheng2)Qiu Rendong Guo Jinxue
(Research Institute of Base and Foundation，China Academy of Building Research，Beijing 100013，China)

It is assumed that the failure of geomaterials is determined by stress ratio between shear stress and normal stress on the characteristic surface based on its friction behavior.The concept of e ff ective stress ratio is proposed and it is expressed by the ratio between shear stress and normal stress on characteristic surface.The stress ratio on characteristic surface can be expressed as the tangent value of straight line deducted by the intercept circumscribing the mohr’s circle in σ-τ coordinates in two-dimensional condition.It is assumed that there is a three-dimensional physical space plane in XYZ space considering every two adjacent physical coordinate plane under three-dimensional space.The shear stress ratio on characteristic surface in three-dimensional space is the determinant factor influencin the failure behavior of material and the proposed criterion can be signed as a criterion.SMP(spatially mobilized plane)criterion and generalized Misescriterion are two special cases of the a criterion.When the value of intercept in two-coordinates is zero,the proposed criterion is degenerated to SMP criterion.When the value of tangent is zero,the proposed criterion is degenerated to generalized Mises criterion.When the intercept and angle of circumscribing line are not zero,the proposed criterion in deviatoric plane is between the above those.The curved triangular form is exhibited between the curves of SMP criterion and generalized Mises criterion in deviatoric plane.A coupling of compression and shear behavior yield criterion is adopted and a power function is adopted as failure criterion.A shape function is proposed based on the proposed criterion in deviatoric plane.The criterion expressed by p and q is substituted by the proposed criterion expressed by three dimensional stresses and the transformation stress equations are deduced based on proposed criterion.In general a constitutive model expressed by p and q can be converted as a three-dimensional model simply.Through yield and strength behaviors and a variety of stress paths test contrast,the rationality of the proposed criterion and transformation method are verified

geomaterials，failure，strength criterion，yield criterion，stress path

TU43

：A

10.6052/0459-1879-16-297

2016–10–26 收稿，2017–03–16 录用,2017–03–16 网络版发表.

1)国家自然科学青年基金(11402260)、中国建筑科学研究院应用技术研究基金(20141602330730038)、住建部科技计划研究基金(20161602420730011)资助项目.

2)万征，副研究员，主要研究方向：地下结构与土相互作用，混凝土及土的本构关系.E-mail：zhengw111@126.com

万征,秋仁东,郭金雪.岩土的一种强度准则及其变换应力法.力学学报,2017,49(3)：726-740

Wan Zheng,Qiu Rendong,Guo Jinxue.A kind of strength and yield criterion for geomaterials and its transformation stress method.Chinese Journal of Theoretical and Applied Mechanics,2017,49(3)：726-740