关注学案设计 着意课堂实效

童卫军

[摘 要] 笔者在教学实践中，关注学案设计，通过“因学而设”“因练而设”“因得而设”等策略，让课堂教学更多地具有“先学后教、因学设导、顺学而导、多学少导”的常态，激发了全体学生参与学习的兴趣，提高了课堂教学实效.

[關键词] 因学而设；因练而设；因得而设；课堂实效

纵观现在的初中数学课堂，普遍存在以教师的“教”垄断课堂时间的现象. 发言的总是那么几个唱主角的，许多学生无所事事当着听众，出现了“教”与“不教”是一个样的无效或低效结果. 究其原因，源于课堂上学生学习实践活动的缺失，换言之，教师的过度讲析严重侵占了学生的学习时间和发展空间，教师“指令性”的教学，常常置学生于“被应答”“被聆听”的消极处境. 离开了参与实践，学生便无法对数学学习产生真正的兴趣，也不可能在“用数学”中提高数学素养.

如何改变课堂教学中“高耗低效”的现状，实现全体学生参与学习课堂？2011版的《全日制义务教育数学课程标准》（以下简称《标准》）指出：“教学活动是师生积极参与、交往互动、共同发展的过程. 有效的教学活动是学生学与教师教的统一，学生是学习的主体，教师是学习的组织者、引导者与合作者. ”笔者基于对《标准》的解读，进行了以学案为载体的数学课堂实践与研究，使课堂教学更多地具有“先学后教、因学设导、顺学而导、多学少导”的常态，提高了课堂教学效率. 那么，以学案为载体的课堂有哪些有效策略呢？

因学而设，了解学习起点

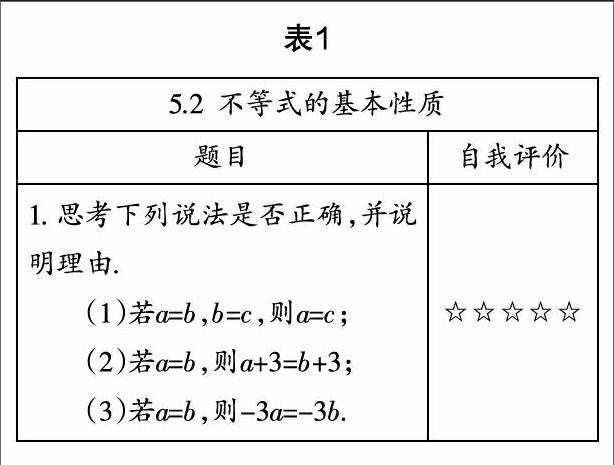
课堂是学生的课堂，是学生充分施展才能、取得学习成果的时空，教师得为学生的学习服务. 备课时，教师应从学生的角度出发，通过对学生预习情况的了解，明确学生学习的兴趣点和困惑点，准确把握教学的起点，针对学生的实际需要进行有效教学. 因此，设计课前学案就显得十分重要. 它既能让教师判断学生学习的难点，切实把握学生学习的需求，做出比较准确的学情分析，又有利于学生清楚地知道预习要做什么，要怎么做. 比如，教学浙教版《义务教育课程标准实验教科书·数学》八年级上册“5.2不等式的基本性质”一节，笔者设计了如下课前学案（见表1），让学生按照要求完成，然后进行自我评价.

教师对学生完成的课前学案进行整理后，得出以下几个问题：

（1）对于等式的三个基本性质，绝大部分学生会应用和区分，但不能用准确的文字或表达式进行叙述.

（2）学生难以解决的问题是第2题的第（3）小题，第4题的第（7）（8）（9）小题及依据的填写，第5题解题不完整.

（3）难以理解的知识是不等式的基本性质3.

（4）研究的问题主要有：不等式的基本性质与等式的基本性质的联系与区别；不等式的基本性质的推理证明；不等式的基本性质的运用；分类讨论思想.

课堂中，根据课前学案反映的问题，笔者重点交流学案中学生难以理解的不等式的基本性质3，并对不等式的两边同时乘一个负数必须改变不等号的方向进行重点指导，以让学生认真练习、巩固，对“不等式的基本性质”的把握进行方法的总结，最后，把学生提出的问题展示在屏幕上，让学生进行分析、归类：“哪些问题其实是表达同一个意思？在这些问题中最核心的是什么问题？”在教师的引导下，学生确定了核心问题和自主学习目标为不等式的基本性质3. 接下来，教师就可以自然地给出第二次自主学习要求. 对于需要独立学习的试题，就由个人向大家交流，而对于小组合作学习的试题，需汇总后派代表向大家交流. 这样做的目的是让每个学生都参与进来，不做学习过程的看客. 这样围绕核心问题的讨论，能让学生自主解读不等式的基本性质，能培养他们自己提出问题和解决问题的能力. 课前学案改变了课堂结构，让课堂呈现出“先学后教”“以学定教”的状态.

与学生认真完成课前学案一样，教师只有在备好课前学案的基础上认真备课，才能在课堂上运筹帷幄，做好学生的“引领者”. 比如，教学浙教版《义务教育课程标准实验教科书·数学》八年级上册“7.2认识函数”一节时，有学生在课前学案上提出了这样一个问题：如何理解对于x每一个确定的值，y都有唯一确定的值？

于是，教学中笔者进行了这样的引导：

给出两个简单的表达式y=x2和y2=x，请学生思考：给定x的一些值，如0，±1，±2，±3…求出y的值进行比较，然后小组交流讨论，给出自己的观点.

生1：对于y=x2，给定一个x的值，y都有唯一一个值. 而对于y2=x，给定x=0时，y=0；给定x为负数时，y不存在；给定x为正数时，y有两个值. 所以，给定一个x的值，y的值不是唯一确定的. 因此，y=x2是y关于x的函数，但y2=x不是y关于x的函数.

生2：对于y=x2，x可以取任何实数，给定一个x的值，y都有唯一一个值，所以y是x的函数. 而对于y2=x，x必须大于等于0，给定x为正数时，y有两个值，所以y不是x的函数.

生3：有两个变量x，y，对于y=x2，给定一个x的值，y都有唯一一个值；而对于y2=x，给定一个y的值，x都有唯一一个值，所以y=x2是y关于x的函数，x是自变量，而y2=x是x关于y的函数，y是自变量.

……

教师总结：函数要抓住其实质，实际上就是一一对应，一个自变量的值对应唯一一个因变量的值.

对于学生在学案中发现的问题，教师灵活引导学生潜心比较与感悟，交流与讨论，学生学得积极主动，学得生动活泼，课堂不再是死气沉沉的泥水潭，而成了汹涌澎湃的思维场. 这足以看出，课堂只有基于学生的学习起点，才会产生效益和价值. 因此，一节有效的数学课堂，应从精心设计课前学案开始，使教学真正促进学生的学习和发展.

因练而设，落实基础训练

《标准》指出：“义务教育阶段的数学课程是培养公民素质的基础课程，具有基础性、普及性和发展性. 数学课程能使学生掌握必备的基础知识和基本技能，培养学生的抽象思维和推理能力；培养学生的创新意识和实践能力；促使学生在情感、态度与价值观等方面的发展. ”每一节数学知识都存在许多教学价值点，教师要重点挖掘隐含着的数学学习价值，重点训练学生对数和形的运算能力和推理能力. 笔者在备课时就特别注重知识的基础训练价值，使学案的设计凸显“双基”的训练. 比如浙教版《义务教育课程标准实验教科书·数学》八年级上册“7.5一次函数的简单应用”一节中“综合运用一次函数解析式和图像解决简单的实际问题”就是最具数学学习价值的，为落实这一数学核心价值训练点，笔者结合课后的探究活动和课题学习设计了如表2所示的学案.

根据问题的特点，该如何去应聘？其实就是比较两公司的工资待遇. 因此，教师在学习单反馈时，应根据学生的学情给予提示，要求给每家公司建立一个工资待遇（y）与销售额（x）之间的函数. 根据函数图像或利用不等式，通过比较，达成解决问题的基本目标，帮助学生感受函数与图像的应用，并深层次地体会数形结合思想方法，最后总结学习方法，把学案贯穿课堂教学始终，让学案帮助学生理解知识，解决问题，感受数学思想方法，掌握学习规律和策略，强化、优化课堂练习，实现“学会”向“会学”转变.

而学案的设计，除了凭借课后练习、探究活动及课题学习，章节中大量的例题解题方法也值得学习、揣摩和变式训练，关键是我们教师要有一双善于发现的眼睛和对数学敏锐的感受能力，把发现的数学方法提炼出来，让学生进行积累运用. 如浙教版《义务教育课程标准实验教科书·数学》八年级上册“5.4一元一次不等式组（1）”一节中，在学案中可以设计如表3所示的练习.

练习是巩固知识、深化知识与发展能力的一种有效手段，只有在课堂上保证学生有充分的时间动脑想一想、动笔练一练，同学之间合作交流探讨，才能真正落实数学的双基训练，提高教学实效，从而真正减轻学生课下的作业负担.

因得而设，注重学法指导

让学生“会学”比“学会”重要得多. 要想让学生在学习中充分地自主学习，其重要前提是教给学生学习方法. 只有当学生获得一定的学习方法时，才有能力自主学习. 《国家中长期教育改革与发展规划纲要》指出：“要倡导启发式、探究式、讨论式、参与式教学，帮助学生学会学习. ”笔者在教学浙教版《义务教育课程标准实验教科书·数学》七年级下册“7.4分式方程”一节时，整理了学生在课前学习单上提出的疑问：为什么分式方程会有增根？为了帮助学生解决难点、获得方法，笔者设计了如表4所示的学案.

利用学案，让学生通过合作探究的方式，用自己的观点去判断，用自己的思维去创新，用自己的语言去表达，充分释放了学生的主动性和创造力，同时保证了每位学生参与学习. 在交流中，教师相机总结学习方法，有时遇到难以理解的问题时，可以通过画图、实验的办法来解决.

另如，学习浙教版《义务教育课程标准实验教科书·数学》八年级下册“5.5平行四边形的判定（1）”这一节时，笔者紧紧抓住边和角进行学案设计，通过画一画、量一量，寻找平行四边形的一些等量关系或位置关系，然后猜想除了用定义判定平行四边形外，是否还有其他的方法. 笔者要求各小组讨论完成表5.

学生在自主研讨后，比较测量结果，自然而然地提出了三个猜想：两组对角分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对边分别相等的四边形是平行四边形. 并利用所学知识给出证明，归纳总结出平行四边形的判定定理. 教师再加以引导，强调课本只给出了“一组对边平行且相等的四边形是平行四边形；两组对边分别相等的四边形是平行四边形”这两个判定定理. 而对于“两组对角分别相等的四边形是平行四边形”，可以在选择题、填空题时使用. 由此可见，课堂上，学案提供了探究的载体，这种实践方式使知识“活”了起来，让每一次学习都成为学生成长的生长点.

课堂教学是学生学习能力培养的主阵地. 笔者从实践中总结出“关注学案设计，着意课堂实效”應该着重关注以下几个方面：一是学案的设计能呈现数学知识的特点，如课前预习时把握本节主要内容，提出困惑；课堂学习时揣摩本节课的重点、难点，领会基础知识与基本技能；最后，理解掌握、积累运用、灵活迁移等. 二是学案的设计要能让学生掌握数的运算和形的推理方法，发展学生的抽象思维和推理能力，培养学生的应用意识和创新意识. 三是学案的设计要能培养学生把握重点内容的能力，循序渐进地教给学生“问题提示、表格辅助、抓住要点”等方法. 四是学案的设计要关注知识冲突，从问题的角度有意识地引导学生发现、总结规律与方法. 只有注重学法指导，让学生一课“一得”或“多得”，才能体现出数学课“增量”的发展.

总之，以学案为载体的数学课堂，避免了教师逐题的讲问、琐碎的对话、无度的拓展，解决了数学教学“高耗低效”的问题，它是一种基于课堂教学原点思维的重构，是学生实现学习和发展的平台，是激发全体学生参与学习的原动力. 数学教师要做一个高明的设计师，关注学案设计，让课堂实现以效率为主的美丽转身.