函数零点与单调性在导数题目中的应用
2017-06-05山东省宁阳第二实验中学271400山东省宁阳一中271400
山东省宁阳第二实验中学(271400) 山东省宁阳一中(271400)
王晓辉● 苏凡文●
函数零点与单调性在导数题目中的应用
山东省宁阳第二实验中学(271400) 山东省宁阳一中(271400)
王晓辉● 苏凡文●
在高中阶段,导数知识主要用来研究高次函数、超越函数的性质,难度较大,有较强的区分度,故在模拟题与高考题中一直肩负着压轴题的重任.本文利用一类与不等式有关的典型导数题目,从函数零点与函数单调性两个视角谈一下一类导数大题的解决办法.
视角一 函数零点
对于超越函数的零点一般要靠观察得到,但也有章可寻,如若函数中含对数式,真数为1时对应的自变量的值一般为函数的零点,而且零点多为0、1、-1、e等.
视角二 函数的单调性
导数研究的函数单调性无外乎三种,我们分别命名为类一次函数、类二次函数、类三次函数,即函数单调递增或单调递减、先增后减或先减后增、先增后减再增或先减后增再减.
类型一 零点与类一次函数
若函数定义域的端点为函数的唯一零点,则对应的函数一般为类一次函数,可利用一次函数的单调性解题.
题目1 (2016新课标Ⅱ文20)已知函数f(x)=(x+1)lnx-a(x-1).

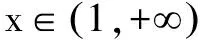
分析 (Ⅱ)中容易发现仅有1为函数f(x)的零点,即f(1)=0,又满足f(x)>0恒成立,所以大胆猜测函数f(x)为单调递增的类一次函数,以此为切入点尝试解题.


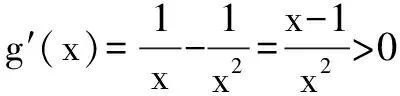
二、零点与类二次函数
此类型题目有两类.
1.若函数定义域内(不含端点)有唯一零点,而函数恒大于或恒小于(亦可恒大于等于或恒小于等于)零,则对应的函数一般为类二次函数,可利用二次函数的单调性来解题.
2.若函数定义域两端点值均为函数的零点,而函数恒大于等于或恒小于等于零,则对应的函数一般为类二次函数,可利用类二次函数的单调性来解题.

(Ⅰ)求l的方程;
(Ⅱ)证明:除切点(1,0)之外,曲线C在直线l下方.
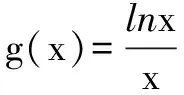

x>1时,1-x2-lnx<0,所以g′(x)<0,g(x)在(1,+)上为减函数,则g(x) 综上可知,除切点(1,0)之外,曲线C在直线l下方. 题目3 (2016年新课标Ⅲ文21)设函数f(x)=lnx-x+1. (Ⅰ)讨论f(x)的单调性; (Ⅱ)证明当x∈(1,+)时,; (Ⅲ)设c>1,证明当x∈(0,1)时,1+(c-1)x>cx. 分析 在(Ⅲ)中,设函数g(x)=1+(c-1)x-cx,容易观察出区间(0,1)的端点值0、1为函数g(x)的两个零点,而需证g(x)>0,故大胆猜测函数g(x)为先增后减的类二次函数,以此为切入点尝试解题. 解析 设g(x)=1+(c-1)x-cx,g′(x)=c-1-cxlnc,g″(x)=-cx(lnc)2<0,所以g′(x)在(0,1)上为减函数. 又g′(0)=c-1-lnc,g′(1)=c-1-clnc. 由(Ⅱ)c>1时,c-1-lnc>0,c-1-clnc<0,即g′(0)>0,g′(1)<0. 所以存在唯一的x0∈(0,1)使得g′(x0)=0, 所以x∈(0,x0)时,g′(x)>0,g(x)在(0,x0]上为增函数,g(x)>g(0)=0; x∈(x0,1)时,g′(x)<0,g(x)在(x0,1)上为减函数,g(x)>g(1)=0. 所以x∈(0,1)时,g(x)>0,即1+(c-1)x>cx. 若函数定义域内有一个端点值为零点,另一个非端点值为零点,而函数恒大于等于或恒小于等于零,则对应的函数一般为类三次函数,可利用类三次函数的单调性来解题. 题目4 (2017年泰安市一轮模拟题20)已知函数f(x)=aex+bx在y轴上的截距为1,并且与x轴相切. (Ⅰ)求a,b的值; (Ⅱ)函数g(x)=x2-2x+1,求证:x≥0时,f(x)≥g(x). 分析 由(Ⅰ)可得a=1,b=-e,设h(x)=f(x)-g(x)=ex-ex-(x-1)2,x≥0时,容易观察出0、1为函数h(x)的零点,而需证h(x)≥0,故大胆猜测函数h(x)为先增后减再增的类三次函数,以此为切入点尝试解题. 解析 由(Ⅰ)可得a=1,b=-e,则f(x)=ex-ex. 设h(x)=f(x)-g(x)=ex-ex-(x-1)2(x≥0). h′(x)=ex-e-2(x-1),h″(x)=ex-2, h″(x)<0时,0 h″(x)>0时,x>ln2,h′(x)为增函数. 因为h′(1)=0,所以h′(ln2)<0, 因为h′(0)=3-e>0,所以∃x0∈(0,ln2),使得h′(x0)=0, 所以x∈(0,x0)时,h′(x)>0,h(x)在[0,x0]为增函数,h(x)≥h(0)=0; x∈(x0,1)时,h′(x)<0,h(x)在(x0,1)上为减函数,h(x)>h(1)=0; x∈(1,+)时,h′(x)>0,h(x)在[1,+)上为增函数,h(x)≥h(1)=0. 综上可知,当x≥0时,h(x)≥0,即f(x)≥g(x). G632 B 1008-0333(2017)13-0016-02三、零点与类三次函数
