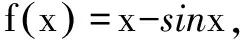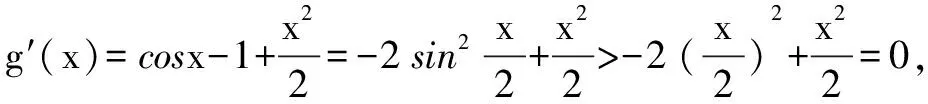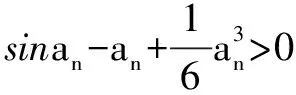构造函数在数列解题中的几例妙用

广西钦州市第一中学(535000)

劳德耀●



构造函数在数列解题中的几例妙用

广西钦州市第一中学(535000)

劳德耀●

函数思想在解决诸多数学问题中起着重要作用，数列作为一种特殊的函数，有关数列的问题可以考虑构造函数来解决.本文略举几例，供高中师生参考．

构造函数;数列解题;应用

一、解决数列求和问题

分析 如若直接从条件an+2=an+1-an入手，化简变形，过程复杂繁琐，因此可以考虑构造抽象函数f(x+2)=f(x+1)-f(x)．

解 设f(n)=an，则f(n+2)=f(n+1)-f(n).

若函数f(x)满足f(x+2)=f(x+1)-f(x)，则f(x+3)=f(x+2)-f(x+1).

两式相加得f(x+3)=-f(x)，则f(x+6)=-f(x+3)，因此f(x+6)=f(x)，

即函数的周期是6，且易求得

f(1)+f(2)+f(3)+f(4)+f(5)+f(6)=0，

而2012=335×6+2,

所以S2012=a1+a2+…+a2012=a1+a2=3．

评析 数列给出递推公式，要求求前n项和的一种情况就是数列是周期数列，当然直接探究其周期性亦简便，然而构造函数更能了解其实质规律，再运用抽象函数的知识进行探究，得出周期，最后得解．

二、解决数列最值问题

分析 易得出nSn是关于n的一个三次函数，解决最值问题可以联想到导数，所以构造函数思想简单直接．

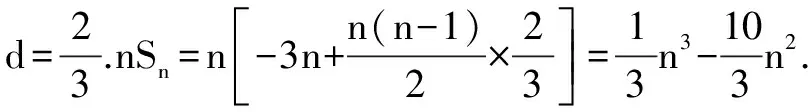
评析 数列中的最值问题，其实大多数可以通过构造函数进行化解，可以构建二次函数，三角函数等，从而就可以采用导数的方法解决，这样的转化大大提高了解题效率．

三、证明与数列有关的不等式

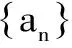
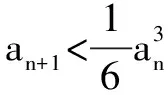
证明 (Ⅰ)先用数学归纳法证明0

①当n=1时，由已知，结论成立.

因为00，

所以f(x)在(0，1)上是增函数.又f(x)在[0，1]上连续，

从而f(0)

故当n=k+1时，结论成立.

由①、②可知，0

又因为0

综上所述,0

由(Ⅰ)知，当0

所以g(x)在(0，1)上是增函数.

又g(x)在[0，1]上连续，且g(0)=0，

所以当00成立.

评析 从以上两例可看出,对于一阶或二阶递推数列与不等式结合的题目,有时采用构造函数,并利用函数的单调性加以解决,能起到出奇制胜的效果.

[1]杨瑞强.构建函数巧解数列问题[J].中学生数学，2012(6).

[2]于志洪.构造三次函数解最值问题[J].数学教学，2015(12).

G632

B

1008-0333(2017)13-0019-01