基于飞机竖向加速度的道面不平度限值标准研究

程国勇， 侯栋文， 黄旭栋

(中国民航大学 机场学院，天津 300300)

基于飞机竖向加速度的道面不平度限值标准研究

程国勇1， 侯栋文1， 黄旭栋1

(中国民航大学 机场学院，天津 300300)

对于机场道面的平整性，目前国内外相关标准仅做了一般性规定，而未根据不同部位的重要性加以区分；实际上相同的不平整程度在飞机的不同滑行状态下导致的颠簸效果有很大的差别。针对这一问题，采用飞机整机模型建立飞机-道面振动方程，基于该振动方程构建了不均匀变形道面的Simulink仿真评价系统；以飞机竖向加速度0.4g作为评价标准，利用上述仿真评价系统求解在不同平整程度道面上的振动响应，选取飞机滑行时的三个代表速度分别为0.2v0、0.5v0和0.8v0。分析结果表明：0.2v0、0.5v0和0.8v0三种代表速度在3 m最不利波长条件下，其最大允许变形波幅分别为0.05 m、0.027 m和0.023 m；该结论可以为分析道面不同部位平整程度提供重要依据。

不均匀变形；平整度；整机模型；Simulink仿真；评价系统

由于设计、施工和复杂的岩土环境等原因，机场道面在机轮荷载和自然因素的反复作用下，常常会出现不均匀变形现象。当飞机滑跑经过这一区域时，飞机振动不仅降低了飞机起飞过程中乘客的舒适度并干扰了飞机的操控性能；同时振动会加速飞机结构及起落架的疲劳；另外，颠簸会加大飞机对道面的冲击作用并进一步加剧道面的不均匀变形，最终大大缩减道面的使用寿命。为保证飞机平稳滑行，国际民航组织ICAO及我国对民航机场道面的平整度有相关规定。ICAO认为[1]:在45 m的道面间距内，变形为2.5～3 cm时不会严重地影响飞机的运行；最大可予接受的偏差会随着航空器的类型和速度改变，总体上是表面不平坦的最大高度会随着可予接受不平坦的最低长度增大而增大。中国民航局在2007年颁布的CCAR-140《民用机场运行安全管理规定》中提到[2]：水泥混凝土道面必须完整、平坦，3 m范围内的高低差<10 mm。

实际上，由于机型以及在道面不同部位滑行速度的差异，道面不平整导致的飞机颠簸效应和道面受到的冲击效果差别巨大，但目前国际及国内关于道面不均匀变形的评价方法及标准并没有与道面部位及机型关联。依据目前的国内外技术标准无法为已经出现不均匀沉降道面的维护与风险评价提供具体的参考。部分学者就道面不均匀变形的坑槽问题进行了研究。例如，胡春飞等[3-4]基于1/4车模型研究了跑道上坑槽的许可深度值，提出了坑槽深度的计算公式，所提出公式对滑行速度进行了分段，根据公式只能得到该段速度下所对应的最大凹陷标准；蔡宛彤等[5]利用机械系统软件ADAMS，根据跑道和滑行道速度的不同得到了3 m最不利波长下的道面平整度的最大凹陷标准：滑行道道面平整度的最大凹陷标准为57 mm；跑道在滑行速度为350 km/h时对应的最大凹陷标准为12 mm，在滑行速度为290 km/h时对应的最大凹陷标准为19 mm。所提出的标准只是采用了滑行道和跑道上的代表速度，而实际上飞机在跑道上的速度是随着道面位置的变化而变化。可以看出，现有的研究只是在一定范围内对不同凹陷的道面进行了分析，目前尚不能对道面任一具体的沉陷区域做出判断。

基于上述考虑，本文从飞机在道面上滑行时整机模型的振动方程出发，依据飞机竖向加速度限值的规定，采用Matlab软件构建了Simulink仿真评价系统。以道面实际测线高程为输入数据，利用该系统可对飞机在道面上滑行时的振动响应进行分析，以飞机滑行时竖向振动加速度限值为标准可判定道面平整度是否合格。该成果可为机场道面不均匀变形分析及维护决策提供参考。

1 仿真评价系统的建立

本文要建立的仿真评价系统包括三个部分，分别为道面激励子系统、振动处理子系统和评价指标处理子系统。

1.1 道面激励的建立

飞机的振动响应是衡量道面平整度的依据，而道面的不平整是引起飞机振动的根本原因，故一般从振动角度将道面的不平整称作道面激励。为求解在道面上滑行飞机的振动响应，首先需要构建道面激励的数学模型。按不平度类型将道面激励分为随机激励和离散事件激励，前者是由一般道面的随机不平产生的，后者是由弓形道面、波形道面或凹陷道面等离散事件引起的[6]。对于道面实际的不均匀变形，其实就是这两种类型激励的叠加。本文中，随机激励采用谐波叠加法[7]构建，时域道面随机位移输入见式(1)。离散事件激励采用假定的定量函数来构建，定量函数见式(2)。

(1)

式中：Gq(fmid-i)为功率谱；Δf为频率区间；θ为[0，2π]上均匀分布的相互独立的随机变量；fmid-i为每个小区间的中心频率；t为时间。

q(t)=-0.5H*(1-cos(2πvt)/L)

(2)

式中：H为凹陷道面最大波幅；L为凹陷道面长度；v为飞机滑行速度；t为时间。

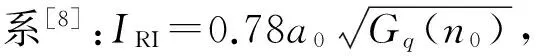
调用Simulink工具箱里面的相应模块建立飞机的机场道面平整度模拟评价系统中的道面激励子系统如图1所示。

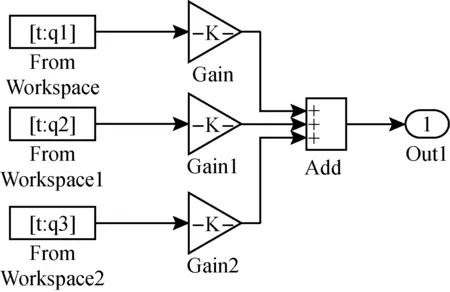
图1 道面激励子系统Simulink模型

该子系统包含模块：From Workspace-模块；From Workspace1-模块；From Workspace2-模块；Gain-增益模块；Gain1-增益模块1；Gain2-增益模块2；Add-加法模块；Out1-输出端口模块1。其中：From Workspace模块的功能为从工作空间和存储工作区中读取数据作为输入信号；Gain模块的功能是使输入的信号乘以一个向量，使信号转化为向量的形式；Add模块的功能是对两个或多个信号进行求和运算；Out1模块的功能是将信号输入到下一级。

1.2 飞机-道面振动方程的建立及求解

为客观分析所有起落架下部道面起伏情况对飞机的产生的振动效果并结合目前民航客机起落架构型，建立机场道面平整度分析的整机模型[10]，如图2所示。

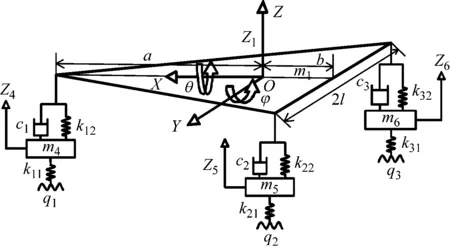
图2 六自由度整机模型

在飞机质心处建立空间直角坐标系，x方向为飞机滑行方向，y方向为飞机侧向，z方向为铅垂方向。图2中其它各符号的含义如下：

m1为机身的质量；m4，m5，m6为轮胎的质量；k11，k21，k31为轮胎刚度；k12，k22，k32为悬架弹性元件的刚度；c1，c2，c3为悬架阻尼器的阻尼；a为飞机质心到前起落架的距离；b为质心到两后起落架连线的垂直距离；2l为主起落架之间的距离；θ为飞机的横向滚转角；φ为飞机的纵向俯仰角。

根据图2整机模型，运用牛顿定律建立系统运动的微分方程，通过整理用矩阵的形式表示为

(3)

{Z}={z1,φ,θ,z4,z5,z6}T

(4)

(5)

(6)

{q}={q1,q2,q3}T

(7)

式中：M为系统质量矩阵；C为系统的阻尼矩阵；K为系统的刚度矩阵；Kt为轮胎刚度矩阵。

它们的值分别为

[M]6×6=diag{m1,Jy,Jx,m4,m5,m6}

(8)

(9)

(10)

(11)

根据式(3)～式(11)，利用Simulink工具箱中Continuous模块库中的相关模块建立模型系统的振动处理子系统，如图3所示。

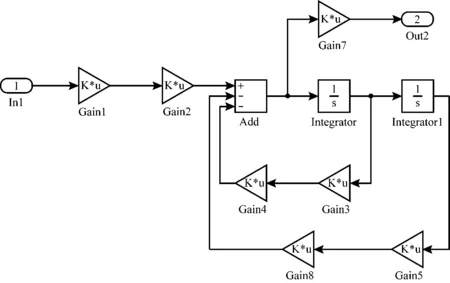
图3 振动处理子系统Simulink模型

该系统中所包含模块有：In1为输入模块1；Gain1为增益模块1；Gain2为增益模块2；Gain3为增益模块3；Gain4为增益模块4；Gain5为增益模块5；Gain6为增益模块6；Gain7为增益模块7；Add为加模块；Integrator为积分模块；Integrator1为积分模块1；Out2为输出端口模块2。其中，In模块的作用是作为子系统里面的一个接受外部输入的一个端口从子系统的上一级接受变量向量；Integrator模块的作用是对信号进行积分。

1.3 评价指标的确定及建立Simulink模型

目前的研究表明，当飞机的竖向加速度超过±0.4g时，飞机将产生较为激烈的振动，飞行员和乘客的舒适度将明显下降，飞机长期在这种条件下运行，会很快降低起落架和机身结构以及跑道道面结构的疲劳寿命[11]；当飞机的竖向加速度在±0.4g的范围内，则跑道的平整度是可以接受的。因此，本文所建立Simulink评价系统中将采用±0.4g作为评价标准。

调用Simulink工具箱里面的相应模块建立飞机的机场道面平整度模拟评价系统中的评价指标处理子系统，如图4所示。

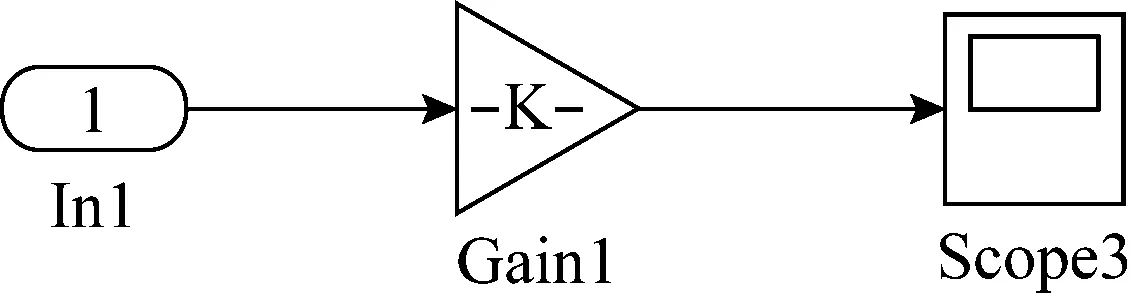
图4 评价指标处理子系统Simulink模型

该系统中所包含模块有：In1为输入端口模块；Gain9为增益模块9；Scope为示波器模块。其中，Scope3模块的作用是显示仿真期间产生的信号。

将各子系统系统进行组合即得到完整的仿真评价系统。

2 评价系统的实例分析

2.1 仿真参数的确定

六自由度飞机模型可选取任意一种起落架形式为前三点式飞机的参数作为计算参数，本文以波音737-800型飞机原始数据[12-14]为例，选取模型参数如下

m1=7.35×104kg；m4=256 kg；m5=m6=1 146 kg；Jx=2.61×106kg·m2；Jy=3.66×106kg·m2；a=14.45 m；b=1.15 m；k11=1.78×106N/m；k21=k31=1.28×107N/m；2l=5.7 m；k12=9.5×105N/m；k22=k32=2.76×106N/m；c1=1.81×104N/m/s；c2=c3=1.08×105N/ m/s。

实际上，道面凹陷的允许最大波幅是根据道面发生凹陷部位的不同而发生变化的，而道面部位又和飞机的滑行速度相关。故而本文假定飞机起飞离地速度为v0=80 m/s，选取三个代表滑行速度：v=0.2v0，0.5v0，0.8v0，分别研究这三个速度所对应道面的凹陷标准。

研究表明[15]:针对1～100 m的波长对飞机的动力响应进行了分析，飞机在滑行时最不利波长为3 m和6 m。鉴于“3 m直尺”法常用于机场道面平整度的测试，为便于系统分析结果和当前测试方法起到对比效果，在实例分析时道面模型中将选用3 m波长进行道面仿真分析。

2.2 道面凹陷允许值的分析

根据道面不同部位，道面仿真速度分别取为：16 m/s、40 m/s和64 m/s，道面凹陷波长均取值为3 m。下面利用所建立仿真评价系统分别进行仿真计算，得到道面这三处道面的标准。

2.2.1 道面上v=16 m/s处

滑行速度为16 m/s，凹陷区域波长为3 m。经过试算波幅的取值区间定为0.03～0.05 m，间隔为0.01 m，分别为编号1～编号3，见表1。

表1 3 m波长道面波幅高度表

根据前述“1.1”节中道面激励时域模型的建立方法，为方便研究，假定三条轮迹带下对应的凹陷道面高程一致，通过编写程序可建立道面模型。 使用plot命令，即可绘出道面激励沿道面纵向的分布图。下面给出波幅为0.03 m时对应的三条测线高程图，如图5所示。

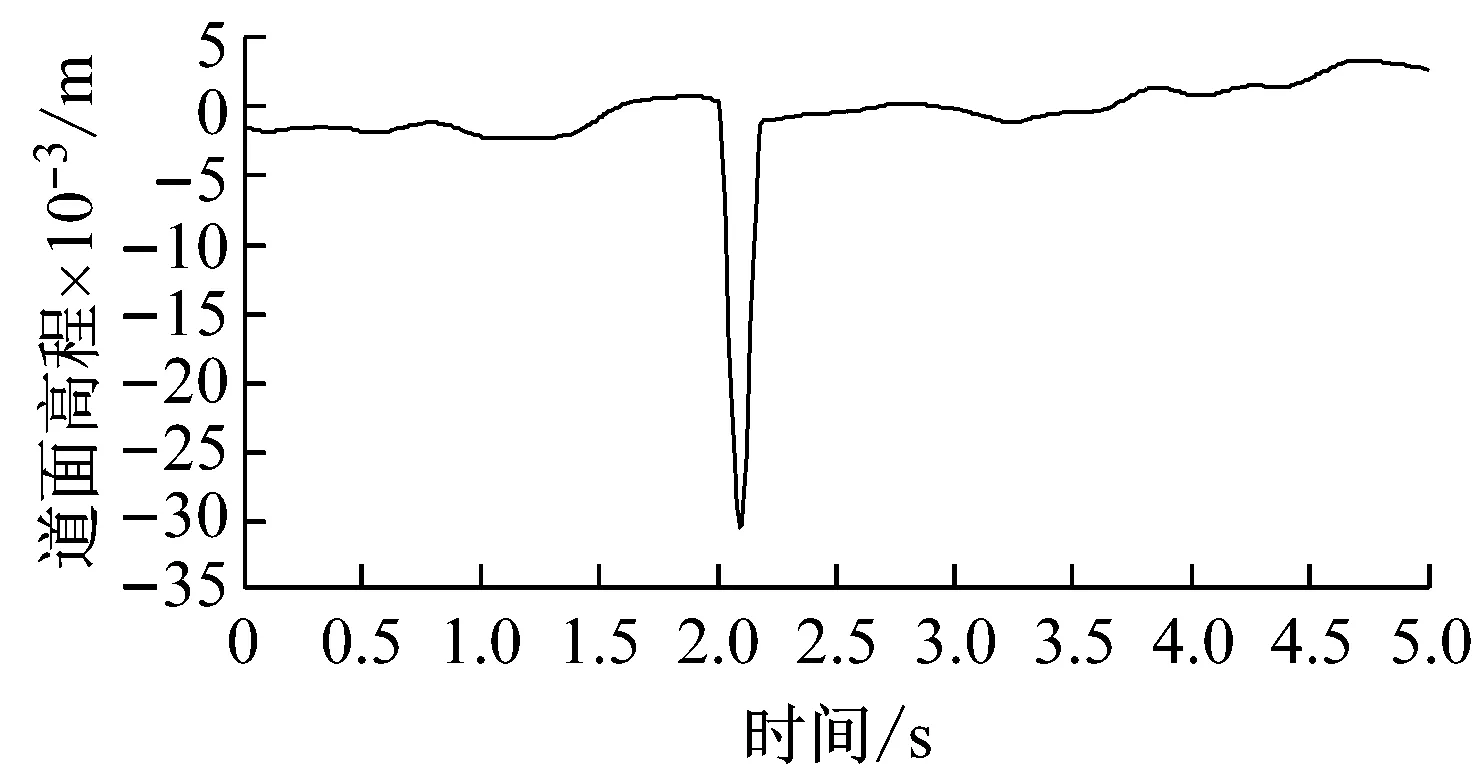
(a) 左测线道面激励

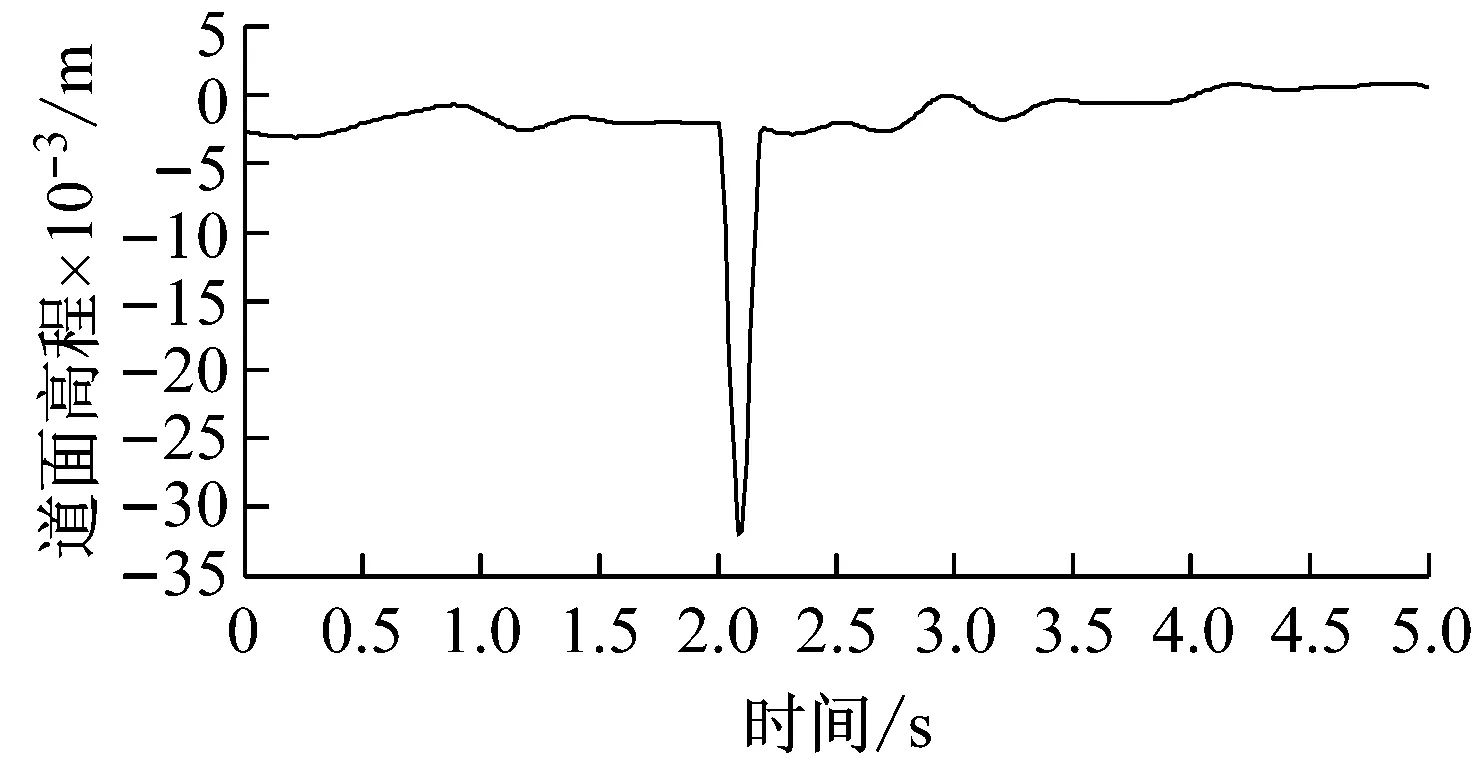
(b) 右测线道面激励

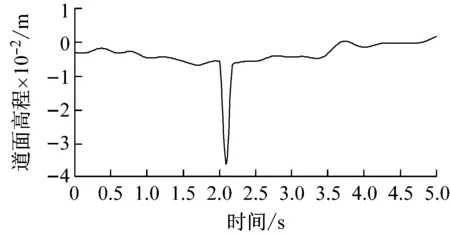
(c) 中间测线道面激励

本文取模拟道面运行时间为5 s。通过对3组波幅进行运行仿真，结果见表2。仿真系统对模拟道面进行仿真的部分竖向加速度响应，见图6～图7。

图6 波幅为0.03 m时的竖向加速度

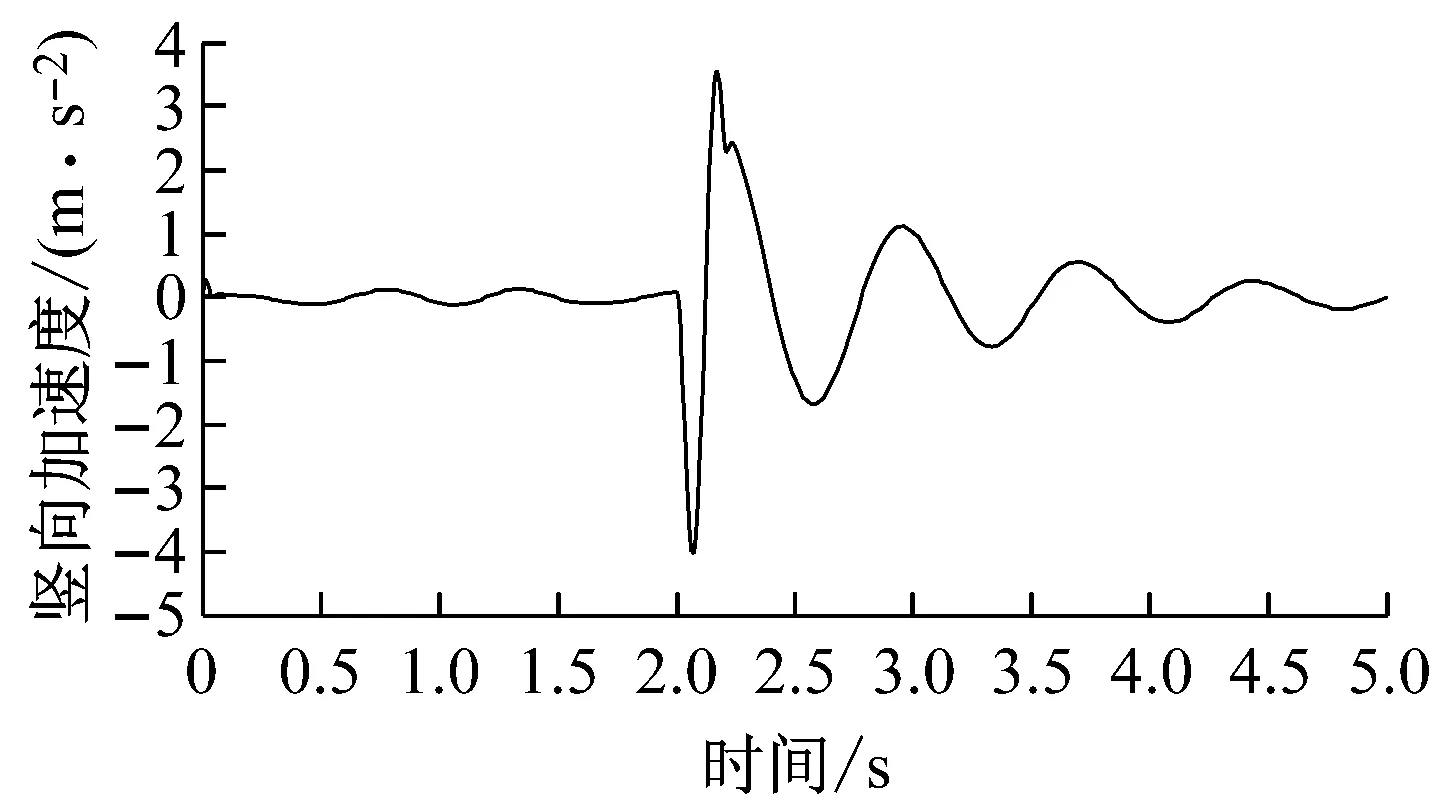
图7 波幅为0.05 m时的加速度

由图6可分析飞机滑行时的整个振动过程：飞机在前2 s道面上滑行时竖向加速度基本上在0上下波动，说明此时道面基本平整。从2～2.2 s内加速度波动比较大，这段表明飞机滑行正经过波长为3 m,波幅为0.03 m的凹陷区域，在这区间内加速度先减小到最大值，说明飞机加速度向下，处于失重状态；后半段加速度增大到最大值，说明飞机加速度向上，处于超重状态。在2.2 s以后飞机的加速度越来越小，飞机的竖向振动逐渐减弱，慢慢趋于平稳。

从表2仿真结果可以看出，根据0.4g的不舒适度评价标准，当飞机以测试速度16 m/s滑行经过波长为3 m的变形道面时，机场道面允许的最大波幅应在0.05 m。即：在3 m不利波长条件下，波幅达到0.05 m时飞机竖向加速度达到0.4g，波幅大小不能超过0.05 m。

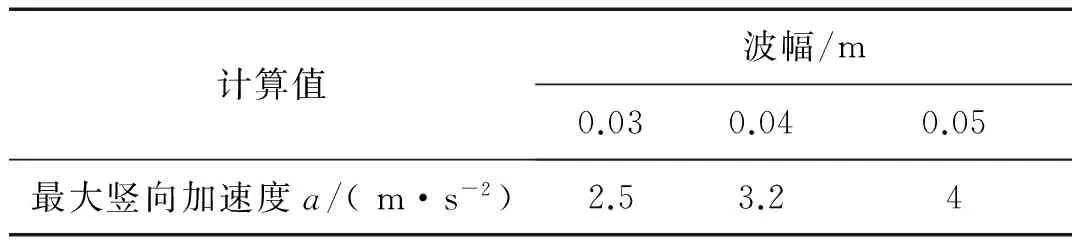
表2 飞机在3 m波长滑行时最大竖向加速度

2.2.2 道面上v=40 m/s处

滑行速度为40 m/s，凹陷区域波长为3 m。经过试算波幅的取值区间定为0.02～0.04 m，间隔为0.01 m，分别为编号1～编号3，见表3。

表3 3 m波长道面波幅高度表

通过对3组波幅进行运行仿真，结果见表4。

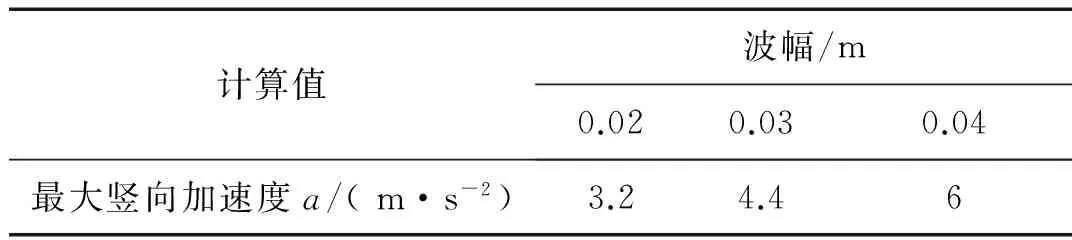
表4 飞机在3 m波长滑行时最大竖向加速度

由表4仿真结果可知，当飞机以速度40 m/s滑行经过波长为3 m的变形道面时，机场道面允许的最大波幅应介于0.02～0.03 m，采用插值法可求得为0.027 m。

2.2.3 道面上v=64 m/s处

滑行速度为64 m/s，凹陷区域波长为3 m。经过试算波幅的取值区间定为0.01～0.03 m，间隔为0.01 m，分别为编号1～编号3，见表5。

表5 3 m波长道面波幅高度表

通过对3组波幅进行运行仿真，结果见表6。

表6 飞机在3 m波长滑行时最大竖向加速度

由表6仿真结果可知，当飞机以速度64 m/s滑行经过波长为3 m的变形道面时，机场道面允许的最大波幅应介于0.02～0.03 m，采用插值法可求得为0.023 m。

3 结 论

(1) 本文采用整机模型，建立了道面-飞机振动方程，以飞机竖向加速度0.4g限值作为评价标准，基于振动方程构建了不均匀变形道面的Simulink仿真评价系统。

(2) 选取了三个飞机滑行时的代表速度0.2v0、0.5v0和0.8v0，利用所建立仿真评价系统对三个代表速度所对应的道面进行了仿真分析。结果表明：三种代表速度在3 m波长下最大允许凹陷波幅分别为0.05 m、0.027 m和0.023 m。

(3) 随着速度的增大，同一凹陷波长道面允许沉陷的最大波幅越来越小。这是由于随着飞机速度的增大，飞机的振动越来越明显。但由于本文的模型无法考虑飞机升力的影响，所以当速度较低时，所得竖向加速度比较准确；当速度较大时，升力比较明显时，本文所得竖向加速度会偏大，使得道面凹陷限值偏小，这样也使得评估道面时偏于安全。

(4) 飞机在道面上滑行时所产生的竖向振动响应与道面的变形部位、变形的波长和波幅均有关联。在判定某一沉陷道面是否合格时，首先需确定飞机通过该部位道面时的滑行速度，然后通过实地测量得到该部位的道面高程，最后输入到本文所建立的仿真评价系统，即可算出飞机滑行通过时的振动响应量，可为机场管理人员进行道面维护决策提供参考。

[1] 机场设计和运行：国际民用航空公约(附件14)[M]. 6版.[S.l.]：国际民用航空组织，2009.

[2] 民用机场运行安全管理规定：CCAR-140 (191号令)[S].北京：中国民航局，2007.

[3] 胡春飞，韩卿爱，吕耀志，等.机场跑道破损坑槽对飞机滑跑动力的影响[J].重庆交通大学学报，2013,32(4)：717-720.

HU Chunfei, HAN Qinai, LÜ Yaozhi. Airport runway damaged pit slot effect on the aircraft taxiing power[J]. Journal of Chongqing Jiaotong University, 2013,32(4)：717-720.

[4] 盖利庆.军用机场跑道表面平整度分析及处理[D].南京：东南大学，2003.

[5] 蔡宛彤，种小雷，王海服，等.基于ADAMS的机场道面平整度评价方法[J].空军工程大学学报，2014,15(1)：15-19.

CAI Wantong, ZHONG Xiaolei, WANG Haifu, et al. The airport pavement roughness evaluation method based on ADAMS[J]. Journal of the Air Force Engineering University，2014,15(1)：15-19.

[6] 檀润华，陈鹰，路甬祥，等.路面对汽车激励的时域模型建立及计算机仿真[J].中国公路学报,1998,11(3)：96-102.

TAN Runhua, CHEN Ying, LU Yongxiang, et al. Pavement on car incentives in the time domain modeling and computer simulation[J]. China Journal of Highway,1998,11(3)：96-102.

[7] 何杰，彭佳，李旭宏，等.路面随机激励时域模型特性的仿真研究[J].武汉理工大学学报，2009,33(5)：919-922.

HE Jie, PENG Jia, LI Xuhong, et al. The road random excitation simulation research the characteristic of time domain model[J]. Journal of Wuhan University of Technology，2009,33(5)：919-922.

[8] 薛华鑫.飞机滑行状态下振动频率响应分析[D].天津：中国民航大学，2014.

[9] 陈龙，何草丰.基于Simulink的路面不平度时域模型仿真研究[J].科技信息，2012(7)：367-368.

CHEN Long, HE Caofeng. Simulation of the domain model of road roughness based on Simulink[J]. Science and Technology Information，2012(7)：367-368.

[10] 余志生.汽车理论[M].北京：机械工业出版社，1998.

[11] 王维，邓松武.机场跑道道面平整度评价及其影响分析[J].中国民航学院学报，2006，24(2)：10-15.

WANG Wei, DENG Songwu. Airport runway surface flatness Evaluation and Impact Analysis[J]. Journal of China’s Civil Aviation College, 2006，24(2)：10-15.

[12] 刘莉，杨国柱，何庆芝.飞机地面滑行随机振动分析[J].航空学报,1993,14(4):126-132.

LIU Li, YANG Guozhu, HE Qingzhi. Aircraft taxi random vibration analysis[J]. Journal of Aviation,1993,14(4):126-132.

[13] 刘莉，杨国柱，何庆芝.起落架缓冲系统参数对飞机滑行状态响应的影响[J].航空学报,1992, 13(6):266-273.

LIU Li, YANG Guozhu, HE Qingzhi. The landing gear buffer the influence of system parameters on the aircraft taxiing state response[J]. Journal of Aviation, 1992, 13(6):266-273.

[14] 顾诵芬.飞机总体设计[M].北京：北京航空航天大学，2001.

[15] 吴庆雄，陈宝春，奚灵智.路面平整度PSD和IRI评价方法比较[J].交通运输工程学报，2008,8(1)：36-41.

WU Qingxiong, CHEN Baochun, XI Lingzhi. Pavement roughness PSD and IRI evaluation method to compare[J]. Journal of Traffic and Transportation Engineering，2008,8(1)：36-41.

Pavement roughness limit value standard based on aircraft vertical acceleration

CHENG Guoyong, HOU Dongwen, HUANG Xudong

(School of Airport, Civil Aviation University of China, Tianjin 300300, China)

For the airport pavement smoothness, the related standards at home and abroad only give a general provision, but do not distinguish different importances of different parts. In fact, the same pavement roughness level can cause quite different bumpiness effects under different plane taxiing states. To solve this problem, the whole aircraft model was used to establish the aircraft-road surface vibration equation. Based on this equation, the uneven deformation pavement simulink simulation evaluation system was constructed. Then, the plane vertical acceleration of 0.4gwas taken as the evaluation standard, the above simulation evaluation system was employed to solve the vibration responses of road surfaces with different flatness levels. Three representative speeds during planes taxiing were chosen, they were 0.2v0, 0.5v0and 0.8v0. The analysis results showed that three representative speeds under the most unfarorable wave length condition of 3 m lead to, the pavement’s maximum allowable deformation amplitudes to be 0.05 m, 0.027 m and 0.023 m, respectively. This conclusion provided an important basis for the flatness analysis of airportpavement’s different parts.

inhomogeneous deformation; flatness; whole machine model; Simulink simulation; evaluation system

2015-11-02 修改稿收到日期：2016-03-10

程国勇 男，博士，教授，1971年生

侯栋文 男，硕士生，1989年生

U416

A

10.13465/j.cnki.jvs.2017.09.025