基于势流理论的内孤立波追赶数值模拟
2022-09-11李永刚邹丽胡英杰张九鸣裴玉国
李永刚, 邹丽,2,3, 胡英杰, 张九鸣, 裴玉国
(1.大连理工大学 船舶工程学院,辽宁 大连 116024; 2.大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116024; 3.高技术船舶与深海开发装备协同创新中心, 上海 200240)
内波属于重力波,是发生在密度稳定层化海水内部的一种波动[1]。内孤立波是一种特殊内波,只有一个波峰或波谷,在传播过程中波形恒定,能量集中,是一种灾害性的海洋环境因素。
卫星遥感和现场观测表明,内孤立波相互作用是海洋中的常见现象[2-4]。当2个孤立波几乎沿同一方向传播,相互作用时间较长,为“强”相互作用过程[5],孤立波追赶是“强”相互作用中的一种特殊情况。目前针对内孤立波追赶的研究较少,仅部分学者对表面孤立波追赶进行了研究。Lax[6]基于KdV方程,依据2孤立波初始波幅之比将孤立波追赶分成了3类。Weidman等[7]在Lax[6]分类范围内进行了实验研究。Zabusky等[8]发现孤立波追赶后波形保持其初始形状,但存在相位变化。Mirie等[9]通过数值研究也发现孤立波追赶后大波存在相位超前,小波存在相位滞后,但2个孤立波波幅可以恢复到原来的99%,尾波要比孤立波直面碰撞时小得多。Fenton等[10]利用傅里叶级数对孤立波追赶进行了数值求解,发现Lax[3]的分类与其数值结果存在差别。Craig等[11]利用实验和数值模拟也观察到了这种类似的差异,并对Lax[6]的分类结果进行了修正。Tong等[12]基于HPC方法对孤立波追赶进行了数值模拟,并验证了Craig等[11]的分类结果。
此外,内波在传播过程中对海洋表面的辐聚和辐散作用会产生特有的表面特征,合成孔径雷达可以捕捉到此自由表面波,这是发现、探测内波的重要依据,因此有必要揭示内孤立波追赶时的自由表面特征[12-16]。
鉴于内孤立波和表面孤立波有许多共同的特征,本文采用包含自由表面效应的多域边界元数值模型和KdV方程Fourier谱方法离散求解分别对内孤立波追赶进行了数值模拟,探讨了2种方法中不同初始波幅比下内孤立波追赶波形演化过程的差异,并通过考虑自由表面效应的BEM-FS模型,揭示了内孤立波追赶时自由表面波的表现形态。
1 移动计算域多域边界元法
1.1 多域边界元法
内孤立波的雷诺数通常较大[17],粘性效应往往可以忽略不计。Zou等[18]将边界元法进行推广,根据流体密度的不同,将计算域划分为2个计算子域,在无粘无旋不可压缩的2层强分层理想流体中,对内孤立波传播进行了模拟,建立了包含自由表面效应的多域边界元数值模型(以下简称为BEM-FS模型)。计算域如图1所示,图中包含上下2层计算域,其中h1=0.1、ρ1=998和φ1分别代表上层流体水深、密度和速度势,h2=0.9,ρ2=1 025和φ2分别代表下层流体水深、密度和速度势,ai和ηi为界面处内孤立波的波幅和波面高度,asi和ηsi为上层流体自由表面处内孤立波诱导的自由表面波的波幅和波面高度,其中i=1, 2分别代表大、小波幅内孤立波,x轴位于界面处,z轴垂直向上。
上下2层流体速度势满足拉普拉斯方程:
▽2φk=0
(1)
式中k=1, 2分别代表上层计算域和下层计算域。
左右两侧和底部均为不可穿透边界条件:
(2)

图1 内孤立波追赶计算域示意Fig.1 The schematic of computational domain for overtaking of ISWs
上层流体自由表面S1处的动力学边界条件为:
(3)
运动学边界条件为:
(4)
在界面S2处,上下两层流体的法向速度势和压力保持连续,因此满足:
(5)
(6)
通过解析理论给定内孤立波初始波形。当内孤立波波幅与浅层水深之比约大于0.4时,弱非线性的KdV理论将与实验结果存在较大偏差[19]。因此当内孤立波波幅与浅层水深之比a/h1<0.4时,本文使用KdV方程理论解作为初始波形,当内孤立波波幅与浅层水深之比a/h1≥0.4时,采用文献[20]考虑自由表面效应的MCC理论给定初始波形。初始时刻上层流体上表面S1设为水平,经过时间步更新演化,随着内孤立波波形趋于稳定,会在自由表面诱导出相应的自由表面波。
界面S2处,根据内孤立波波形给定速度势的初始法向导数为:
(7)
如图1所示,大波幅内孤立波与小波幅内孤立波在左右两侧,两波初始法相速度势设为正负相同,以实现两波同向传播。在初始时刻,x1和x2处的波面波幅均小于10-5h1,且x2-x1>0.6,以确保在追赶发生前,波形传播已稳定。
关于BEM-FS模型的详细描述以及具体解法,可以参照文献[18]。
1.2 移动计算域
内孤立波追赶为“强”相互作用过程,2个波沿同一方向传播,波与波相对移动速度很慢[5]。因此孤立波追赶需要较长的作用时间及巨大的计算区域,本文提出移动计算域的改进方法,以实现在较小的固定长度计算域内实现内孤立波追赶的数值模拟。
如图1所示,在t1时刻,当左侧大波幅内孤立波每向右传播一个计算网格长度时,下一计算时刻t1+Δt,整体计算域将跟随内孤立波向右移动一个计算网格长度。在t1+Δt时刻,S4~S7边界处速度势认为与t1时刻近似相等,S1~S3处最左边舍弃一个节点速度势和法向速度,最右边增加一个节点,其速度势和法向速度与左侧相邻节点的速度势和法向速度近似相等;反之,当大波向前传播未满一个计算网格长度时,计算域不移动。当内孤立波离固壁S4~S7足够远时,移动计算域与固定计算域相比计算误差很小。图2为内孤立波波谷距固壁20个单位长度时,40 s计算时刻分别采用移动计算域与固定计算域所得的内孤立波追赶波形,由图可知,移动计算域可以实现波形演化的准确模拟。

图2 40 s时移动、固定计算域下内孤立波追赶波形对比Fig.2 The comparison of interface profiles by mobile computational domain and fixed computational domain at 40 s
1.3 网格和时间步无关性验证
以本文最大计算波幅a1/h1=0.4为例,进行网格和时间步无关性验证。
如图3所示,当无量纲化网格尺度Δx/h1<0.5时,波形收敛,为保证计算精度,网格尺寸大小选取Δx/h1=0.4。如图4显示,选取的时间步皆收敛,为保证计算精度,选取Δt=0.01 s作为时间步大小。

图3 BEM-FS模型网格无关性验证Fig.3 The convergence verification of profile in regard to mesh sizes for BEM-FS model
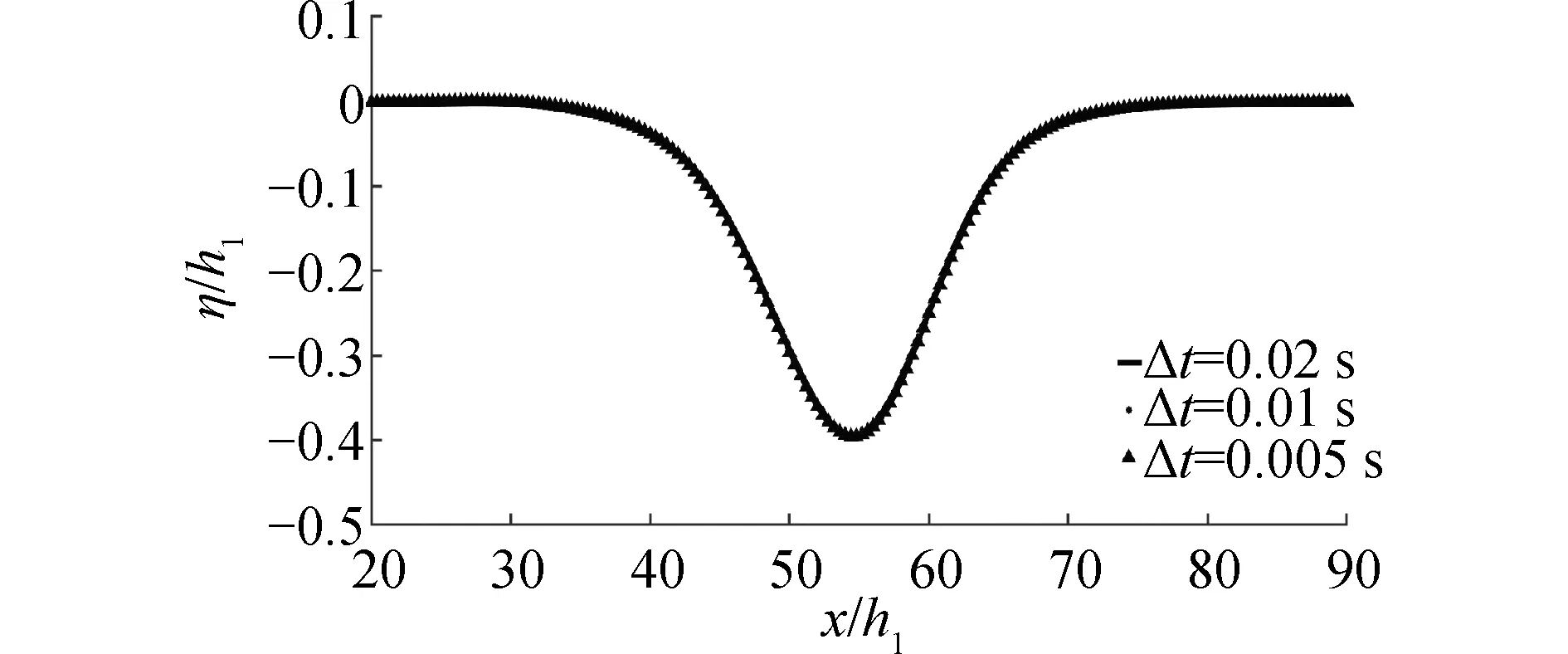
图4 时间步无关性验证Fig.4 The convergence verification of profile in regard to time steps
2 KdV方程Fourier谱方法离散求解
2.1 理论推导
在弱非线性、弱色散条件下,KdV方程的形式为[21]:
ζt+(c0+c1ζ)ζx+c2ζxxx=0
(8)
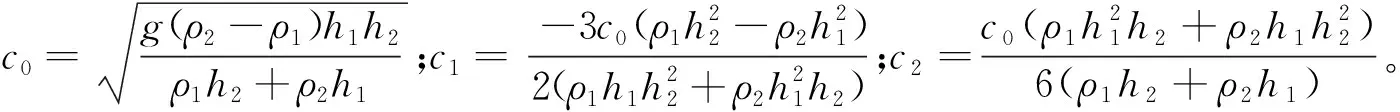
利用Fourier谱方法确定该方程离散格式,对非线性方程(8)线性化得:
(9)
(10)
根据傅里叶变换的微分性质,对时间项采用向前差分为[22]:
(11)
采用四阶龙格-库塔法对其进行迭代求解。则傅里叶变换系数的迭代形式可表示为:
(12)
2.2 网格和时间步无关性验证
为使快速傅里叶变换有效,离散点数应尽可能选择为2的整数次幂。以本文最大计算无量纲化波高a1/h1=0.4为例,采用不同网格尺寸和时间步长,在10个单位长度内,数值模拟内孤立波传播了15 s,对网格和时间步进行了验证,离散设置情况如表1所示。在不同离散设置情况下对内孤立波波形与KdV理论波形进行了比较,如图5所示,设置2~4下波形均收敛,综合考虑时间成本,采用设置3中的网格尺寸和时间步长用于内孤立波追赶的模拟。

表1 离散设置情况

图5 Fourier谱方法网格与时间步无关性验证Fig.5 The convergence verification in regard to mesh sizes and time steps for FSM
2.3 初始条件
根据KdV方程理论解,设定波面初始条件为:
ζ(X)=a1·sech2(X/λ1)+a2·
sech2((X+X1)/λ2)
(13)
式中:a1和λ1分别为大波幅孤立波波幅和特征波长;a2和λ2分别为小波幅孤立波波幅和特征波长;X1为2个内孤立波的距离。在初始时刻,边界处内孤立波波幅以及X1范围内内孤立波波幅均小于10-5h1,以消除壁面效应和确保在波形稳定之前,2波没有发生碰撞。
3 波形演化及追赶分类
3.1 波形演化
图6为文献[20]、本文BEM-FS模型解和KdV方程理论解下不同无量纲化波高a/h1下内孤立波波速的对比图。BEM-FS模型数值解与实验测得波速吻合较好,但KdV理论解波速整体偏小。由于KdV方程Fourier谱方法离散求解和BEM-FS数值模拟2种方法在计算内孤立波波速上存在差异,故本文仅在各自时间轴下分别对内孤立波追赶波形演化过程及其分类进行研究。

图6 内孤立波波速对比Fig.6 The comparison of wave speed of ISWs
Lax[6]基于KdV方程,将非线性演化方程与线性算子关联,依据两表面孤立波初始波幅之比a1/a2,将孤立波追赶分成了3类:



Craig[11]在完全欧拉方程哈密顿系统中利用数值方法对文献[6]的分类进行了修正:



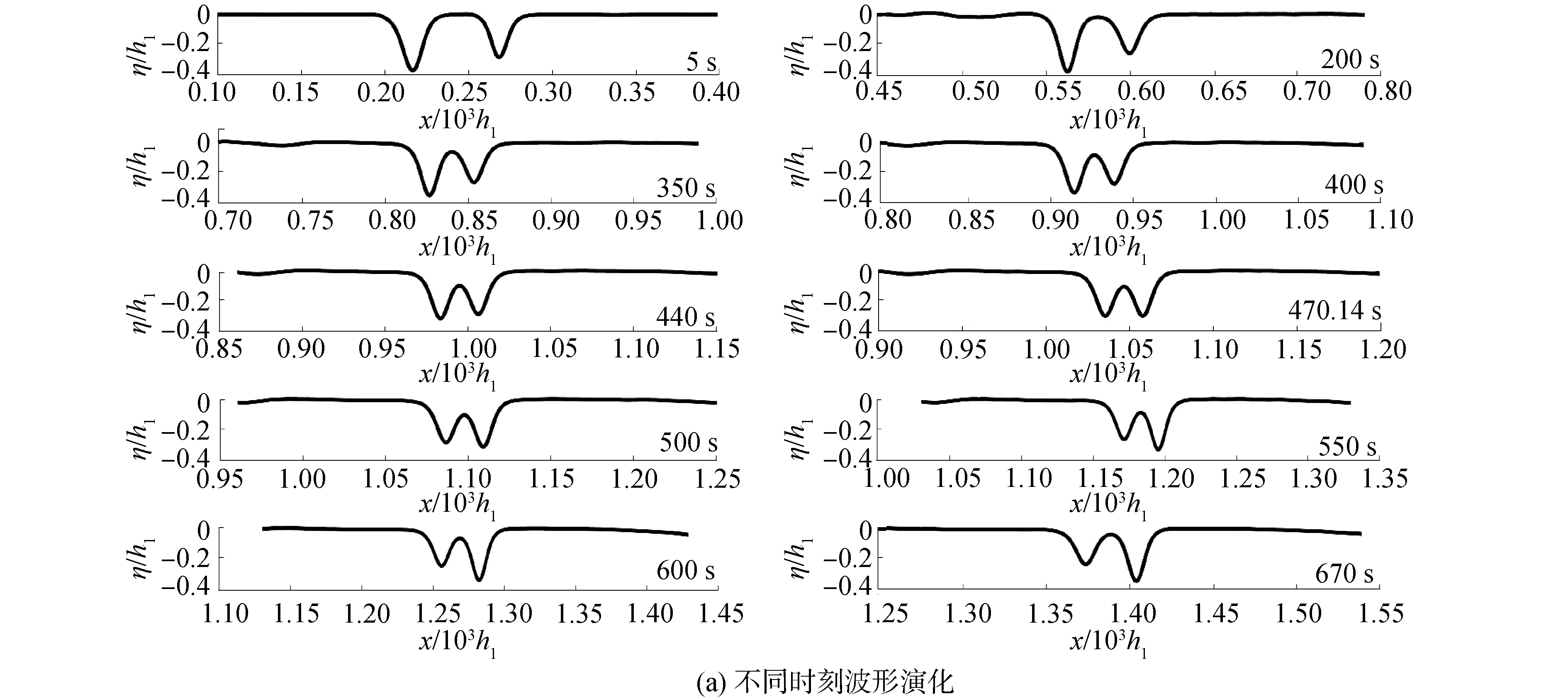
本文一系列波幅比内孤立波追赶波形演化显示,BEM-FS数值模型模拟结果和Craig[11]分类保持一致。当2个内孤立波波幅相差较大,波幅比3.536 图7 BEM-FS数值模型下内孤立波波幅分别为a1/h=0.4,a2/h=0.113追赶波形演化Fig.7 Overtaking of two ISWs of height a1/h=0.4,a2/h=0.113 by BEM-FS 图7(b)时空分布下的波形演化过程图更为形象地展示了类别3内孤立波追赶过程(由于内孤立波追赶作用时间长计算域大,为能在一张图内完整清晰展现作用过程,本文所有时空分布下的波形演化过程图均为相对作用图,即固定大波幅内孤立波的水平位置)。此类别内孤立波追赶在作用中心时刻,会有明显的相互作用过程。 当2个内孤立波波幅比2.941 图8 BEM-FS数值模型下内孤立波波幅分别为a1/h1=0.4,a2/h1=0.133 追赶波形演化Fig.8 Overtaking of two ISWs of height a1/h1=0.4,a2/h1=0.133 by BEM-FS 当2个内孤立波波幅接近,波幅比a1/a2<2.941时,如图9(a)所示,虽然在2个内孤立波追赶过程中,也会出现大波波幅逐渐减小,小波波幅逐渐增大的过程,但在每一计算时刻,都存在2个明确的波谷,在作用中心时刻470.14 s会呈现出比类别2更为明显分离的2个等高波谷。与类别2和类别3的本质不同在于,如图9(b)包含时间轴的三维波形演化过程图所示,在整个计算过程中,大波幅内孤立波并没有将小波幅内孤立波吞没,没有发生大波幅内孤立波追赶并超越前方小波幅内孤立波的明显过程,而是大波幅内孤立波将波幅不断地传递给前方小波幅内孤立波。在作用中心时刻过后,后方内孤立波的波幅继续传递给前方内孤立波,最终导致前方内孤立波波幅增大,后方内孤立波波幅减小,因此在类别1内孤立波追赶整个作用过程中,都是以这种波幅传递的方式完成的。 图9 BEM-FS数值模型下内孤立波波幅分别为a1/h1=0.4,a2/h1=0.3追赶波形演化图Fig.9 Overtaking of two ISWs of height a1/h1=0.4,a2/h1=0.3 by BEM-FS 图10 Fourier谱方法离散求解下内孤立波波幅分别为a1/h1=0.4,a2/h1=0.133…追赶波形演化Fig.10 Overtaking of two ISWs of height a1/h1=0.4,a2/h1=0.133… by FSM 图11 Fourier谱方法离散求解下内孤立波波幅分别为a1/h1=0.4,a2/h1=0.152 67追赶波形演化Fig.11 Overtaking of two ISWs of height a1/h1=0.4,a2/h1=0.152 67 by FSM 与内孤立波直面碰撞出现约为初始波幅2倍的最大碰撞波高不同[21-23],2个内孤立波追赶时,对于所有类别下的波形演化,都存在大波波幅逐渐减小,小波波幅逐渐增大,追赶过程中波形的波幅始终介于初始2个内孤立波波幅之间,Craig[11]在对孤立波追赶的数值研究中也有相同的发现。 以波幅比a1/a2=4内孤立波追赶为例,对初始波幅为a1/h1=0.4内孤立波的波幅大小随时间变化的情况进行了拟合,图12分别为2种方法所得拟合变化曲线。由图可知,初始波幅为a1/h1=0.4的内孤立波在追赶过程中,波幅先逐渐减小再逐渐增大,在作用中心时刻t3,达到波幅的最小值,本文定义此波幅为作用中心波幅a3/h1。 图12 2种方法下幅值随时间变化曲线Fig.12 The curves of trough versus time by two methods 对图12做进一步分析,显示2种方法对于模拟内孤立波追赶存在诸多差异,具体参数对比如表2所示。在KdV方程Fourier谱方法离散求解下,内孤立波经过追赶相互作用后,波幅几乎恢复到原始波幅,但边界元法波幅存在一定的衰减。此外,表1显示2种方法所得作用中心波幅a3/h1以及波幅演化时间也存在分歧。在图12中,取内孤立波初始波幅的80%和90%做水平线,分别与曲线交于2点,定义t4-t2和t5-t1为波幅演化为80%和90%的作用总时间,以作用中心时刻t3为分界点,把作用总时间分别分为作用前时间t3-t2、t3-t1和作用后时间t4-t3、t5-t3。如表2所示,对于其波幅演化到初始波幅80%和90%的作用总时间t4-t2以及t5-t1,边界元法所得作用总时间为KdV方程Fourier谱方法离散求解的2倍左右。在t4-t2时间内,2种方法所得的作用前时间t3-t2和作用后时间t4-t3分别近似相等,这说明此段时间内2种方法皆显示追赶过程几乎是对称的。但在t5-t1时间内,对比作用前时间t3-t1和作用后时间t5-t3显示,KdV方程Fourier谱方法离散求解显示追赶过程几乎对称的,但BEM-FS模型显示追赶过程呈现出明显的不对称性。 表2 2种方法作用参数对比 图13 BEM-FS数值模型下作用中心波幅a3/h1随内孤立波初始波幅比a1/a2的变化曲线Fig.13 The amplitude of acting center a3/h1 versus the amplitude ratio a1/a2 of the initial ISWs by BEM-FS 图14 Fourier谱方法离散求解下作用中心波幅a3/h1随初始内孤立波波幅比a1/a2变化曲线Fig.14 The amplitude of acting center a3/h1 versus the amplitude ratio a1/a2 of the initial ISWs by FSM Zou等[23]在非线性自由表面条件下,对内孤立波“弱”相互作特例——内孤立波直面碰撞作用过程中自由表面波的表现形态进行了研究,其研究表明内孤立波与自由表面波的波形演化在形态和时间上存在明显差异,即当2个内孤立波发生碰撞,伴随着波高增大时,2个自由表面波也会相互融合,但其波高并非一味增大,而是呈现出上下起伏的现象。以上研究结果表明,在内孤立波直面碰撞和追赶中,内孤立波对自由表面波的影响是不同的。当内孤立波传播时,会在自由表面诱导一个与内孤立波极性相反的、波幅小于内孤立波的类孤立波形式的自由表面波,其传播速度与内孤立波传播速度近似相等[18,20,24]。内孤立波诱导的自由表面波会造成海面粗糙度的变化,合成孔径雷达可以捕捉到内孤立波所产生的自由表面波,从而进行内孤立波预报与反演[25-26]。本文在BEM-FS模型中,将上层流体上表面设置为非线性自由表面条件,得到了内孤立波追赶时的自由表面波波形演化过程。以波幅比为a1/a2=2内孤立波追赶为例,图15显示了自由表面波的波形演化,为显示清晰,省略了部分上层流体,且自由表面波扩大了3倍,内孤立波缩小了10倍。如图所示,当2个内孤立波未发生相互作用时,自由表面波的传播速度近似于内孤立波的传播速度,并以类孤立波的形式进行传播;当内孤立波发生相互作用时,自由表面波也开始相互作用;当内孤立波以初始形状发生分离时,自由表面波也以类孤立波的形式发生分离。因此在内孤立波经历长时间的追赶作用过程中,自由表面波也表现出2个孤立波之间的追赶,两者的波形演化在形态和时间上几乎保持一致。 图15 内孤立波追赶时自由表面波波形演化Fig.15 Waveform evolution of free surface waves for overtaking 1)依据两内孤立波波形是否融合成一个类孤立波波形以及是否发生相互作用等演化特征,根据初始波幅之比,可以将内孤立波追赶分为3类。BEM-FS模型数值模拟结果和Craig[11]表面孤立波追赶分类保持一致;KdV方程Fourier谱方法离散求解下内孤立波追赶分类和Lax[6]模拟结果分类保持一致。 2)内孤立波追赶所有类别下的波形演化,都存在大波幅内孤立波波幅逐渐减小,小波幅内孤立波波幅逐渐增大,追赶演化过程中的波形波幅始终介于初始2个内孤立波波幅之间,BEM-FS模型和KdV方程Fourier谱方法离散求解所得的幅值变化曲线存在诸多差异。 3)作用中心波幅拟合曲线存在拐点,BEM-FS模型下曲线拐点位于Craig[11]分类中类别1)和类别2)分界点附近,而KdV方程Fourier谱方法离散求解下曲线拐点位于Lax[6]分类中类别1)和类别2)分界点附近。 4)与内孤立波直面碰撞作用过程中自由表面波的表现形态不同,内孤立波追赶过程中所诱导的自由表面孤立波与内孤立波的波形演化在形态和时间上几乎保持一致。 存在于真实的海洋中的内孤立波追赶,是否也会因为长时间相互作用导致完成追赶过程后波幅存在较大衰减,而呈现出类似于本文边界元法FS条件BEM模型所得的模拟结果,还需相关实验以及现场观测的进一步验证。



3.2 幅值变化曲线


3.3 作用中心波幅变化曲线



3.4 自由表面波表现形式

4 结论
