基于正交数值试验的反应装甲干扰射流参数敏感性研究

拜云山， 冯晓伟， 梁 斌， 冯高鹏

(中国工程物理研究院 总体工程研究所，四川 绵阳 621900)

基于正交数值试验的反应装甲干扰射流参数敏感性研究

拜云山， 冯晓伟， 梁 斌， 冯高鹏

(中国工程物理研究院 总体工程研究所，四川 绵阳 621900)

基于炸药冲击起爆的Lee-Tarver模型，利用AUTODYN有限差分程序对射流侵彻引爆“三明治”爆炸反应装甲，爆轰压力驱动飞板切割射流过程进行了三维数值模拟。针对反应装甲飞板厚度、夹层装药厚度及射流入射角厚度三个影响因素，确定了射流干扰效率的评估指标，采用正交统计试验方法，对射流干扰效率的评估指标进行了参数敏感性研究。结果表明，射流入射角度对射流评估指标横向动量、头部速度及穿透背板时间均具有显著性的影响，呈正比关系，是最主要的影响因素；飞板厚度对射流评估指标均有较大的影响，是第二主要影响因素；夹层装药厚度对射流头部速度影响无明显规律性，对射流穿透背板时间无显著影响。

爆炸力学；反应装甲；正交设计；评估指标；AUTODYN程序

聚能射流是目前对主战坦克最具威胁性的侵彻体，多年来装甲设计者希望找到能够降低射流侵彻能力的有效防护手段[1]。其中，主装甲附加爆炸式反应装甲是目前典型的装甲防护手段，自Held提出用爆炸反应装甲防御聚能装药战斗部以来，人们对这一技术进行了大量研究[2]，并取得丰硕成果。

Mayseless等[3]的研究结果表明，反应装甲通过夹在两层金属板中间钝感混合炸药层的爆炸，驱动金属面板沿法向飞散，飞散的面板截断射流或使射流获得横向速度，导致射流分散、偏移，从而造成射流不能沿轴线到达穿孔孔底，进而大幅度降低射流对主装甲的侵彻威力。对于反应装甲飞板干扰射流的作用，国内学者也作了卓有成效的工作。武海军等[4]采用三维有限元数值模型方法探讨了反应装甲对射流的干扰问题，得到不同放置角的反应装甲对射流的干扰过程和射流被干扰前后的速度梯度曲线。吴成等[5]数值研究了实际尺寸的一代爆炸反应装甲盒(Explosive Reactive Armor，ERA)在起爆后各飞板的运动规律以及相互作用特点。曾凡君等[6]建立了反应装甲在爆轰阶段干扰射流的数学模型，对“乱石模型”进行了简化和进一步定量化。黄正祥等[7]采用数值计算方法模拟了双层反应装甲在聚能射流作用下的爆炸过程，得到反应装甲在起爆后各面板的运动规律和相互作用的过程，以及双层反应装甲面板在不同起爆点条件下的运动规律，并用实验进行了验证。

由于影响射流与爆炸式反应装甲之间相互作用的因素很多，许多细节问题尚未完全认识清楚，目前国内外学者主要侧重于实验研究和理论分析，针对射流与反应装甲相互作用过程的主要特征，提出一些简单的模型概念以及物理分析过程，以求提供一种可能的解释，且在分析过程中忽略一些重要问题，如板的变形、爆轰场作用等问题。工程试验方法是研究射流与爆炸反应装甲相互作用机理的有效途径，据上述干扰机理分析及存在的问题，若采用工程试验方法，将会导致成本投入高、试验周期长、耗费人力大，在一定程度上增加了研究的难度，而且很难确定各因素对射流干扰的影响规律[8]。因此，鉴于工程试验方法的局限性，数值模拟射流与爆炸反应装甲相互作用过程，成为该领域的另一种主要研究途径。本文应用ATUODYN三维动力有限差分程序对射流侵彻引爆反应装甲过程进行三维建模及仿真，利用正交统计数值试验方法对干扰甲射流的各种影响因素进行分析，以期获得爆炸反应装甲对射流干扰的影响规律。

1 计算模型和材料

1.1 计算方法和几何模型

本文中数值模拟可分解为两部分进行，爆轰压垮药型罩形成射流及射流与爆炸反应装甲相互作用。首先模拟二维射流成型，然后应用ATUODYN映射技术，将精细的二维射流结果映射到三维模型空间进行射流与爆炸反应装甲相互作用模拟[9]。

聚能射流的成型包括炸药的爆轰、药型罩的压垮、射流的形成及拉伸。该过程是多物质相互作用的高应变、高应变率的大变形运动，用Lagrange网格难以准确模拟，同时炸药的爆轰压力远大于药型罩紫铜材料强度，压垮过程中可考虑药型罩材料为流体，因此采用Euler网格进行计算，该算法既可以克服因网格单元严重畸变引起的数值计算困难，又可满足实现流体—固体耦合动态分析的需要。反应装甲面板、背板采用Lagrange网格，爆轰产物、空气与靶板之间的作用采用流固耦合算法。

药型罩壁厚1.0 mm；锥顶高5 mm；装药长度68 mm；锥顶角55°。图1给出了药型罩的有限元模型，网格尺寸0.25 mm。采用点起爆，起爆点位于装药尾部中心位置，如图2所示。

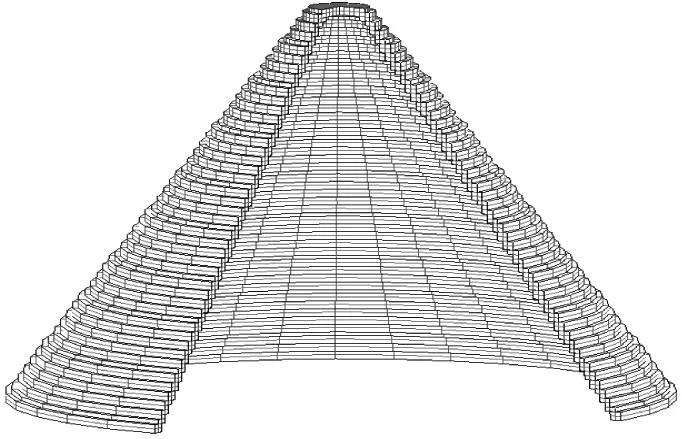
图1 药型罩有限元模型

图2 成型装药起爆位置

反应装甲飞板(面板、背板)取统一厚度，D分别是5 mm、4 mm及3 mm三个值，面积60 mm×20 mm。夹层装药采用军用B炸药，药厚d分别取5 mm、4 mm及3 mm，图3给出了爆炸反应装甲的结构示意图。

图3 爆炸反应装甲模型

1.2 材料模型及参数

药型罩材料为紫铜，爆轰波到达药型罩壁面的CJ压力达数十万个大气压，远大于药型罩材料强度，计算中可视金属材料为流体，压力采用Gruneisen状态方程描述。主要材料模型参数：ρ=8.93 g·cm-3,G=47.7 GPa,Y=0.12 GPa,c=3.94 km/s,s1=1.49,s2=0.6,s3=0,γ0=1.49,a=0.47。

反应装甲面板与背板采用4340高强度钢，材料采用Johnson-cook模型和shock状态方程描述。主要材料模型参数：ρ=7.83 g·cm-3,G=210 GPa,A=350 MPa,B=300 GPa,ν=0.22,C=0.014,n=0.26,m=1.03。

聚能装药及反应装甲中夹层炸药均为Comp.B炸药，主要材料模型参数：ρ=1.717 g·cm-3,D=7.98 km/s,PCJ=20.95 GPa。状态方程采用JWL状态方程来描述，方程参数[10]见表1。

计算中，所有材料模型均采用ATUODYN程序中自带材料模型参数。

夹层炸药冲击响应采用Lee-Tarver三项式点火增长反应模型[11]模拟，该方程可很好地模拟非均匀炸药的冲击起爆特性，见式(1)。基本参数见表2。

G2(1-F)eFfpz

(1)

式中：F为反应质量分数，模拟爆轰过程中控制着炸药化学能的释放，式(1)中具体参数见表2。本文中对描述射流冲击起爆爆炸反应装甲夹层炸药的Lee-Tarver点火增长反应模型，采用文献[12]的模型验证数据。

表1 JWL状态方程主要参数

表2 Lee-Tarver增长模型主要参数

2 正交数值试验设计

正交试验设计是利用已经制好的规格化正交表科学地安排与分析多因素试验的方法。采用正交表，从全部的试验水平(因素状态值)组合中，挑选部分有代表性的水平组合进行试验，并通过对这部分试验结果的数据处理与分析，了解全面试验的情况，找出最适宜水平组合，并预测试验结果。规格化正交表原理设计较多，此处不在赘述，具体可以参考文献[13]。

综合分析国内外相关文献，为简化分析射流与爆炸反应装甲相互作用过程，更好揭示射流对影响因素参数敏感性规律，本文选用典型的“三明治”简化结构作为爆炸反应装甲模型。“三明治”结构爆炸反应装甲干扰射流的影响因素很多，根据对已有的射流侵彻引爆爆炸反应装甲终点效应试验结果分析，同时文献[1]也指出，飞板(面板、背板)厚度、夹层装药量(即装药厚度)、射流入射角是影响干扰射流的三个显著因素变量，需重点考察研究，且交互作用不明显而相对独立，方便利用正交表统计分析其影响规律。本文中该三个显著因素分别记为A、B、C。

为获得这三个主要因素对射流干扰效率的影响规律，采用正交试验设计方法和正交表[14-15]设计数值试验方案。根据正交试验原理，对每个因素变量的水平取值越多，计算结果统计值就越能精确反应影响规律，但取值多将增加更多的试验而耗费巨大的资源，这是很不经济的。为此，选取各因素几个典型水平变动值参与计算分析，可获得射流干扰效率的总体影响规律，将三个参数变化范围初步分为3个水平，计算工况为9种，在不考虑因素间交互作用情况下，将3个影响因素取值安排在规范的正交试验方案表L9(34)的三列上，如表3所示。其中，A、B因素水平值根据反应装甲的结构简化确定，C因素水平值是反应装甲放置的3个典型角度。

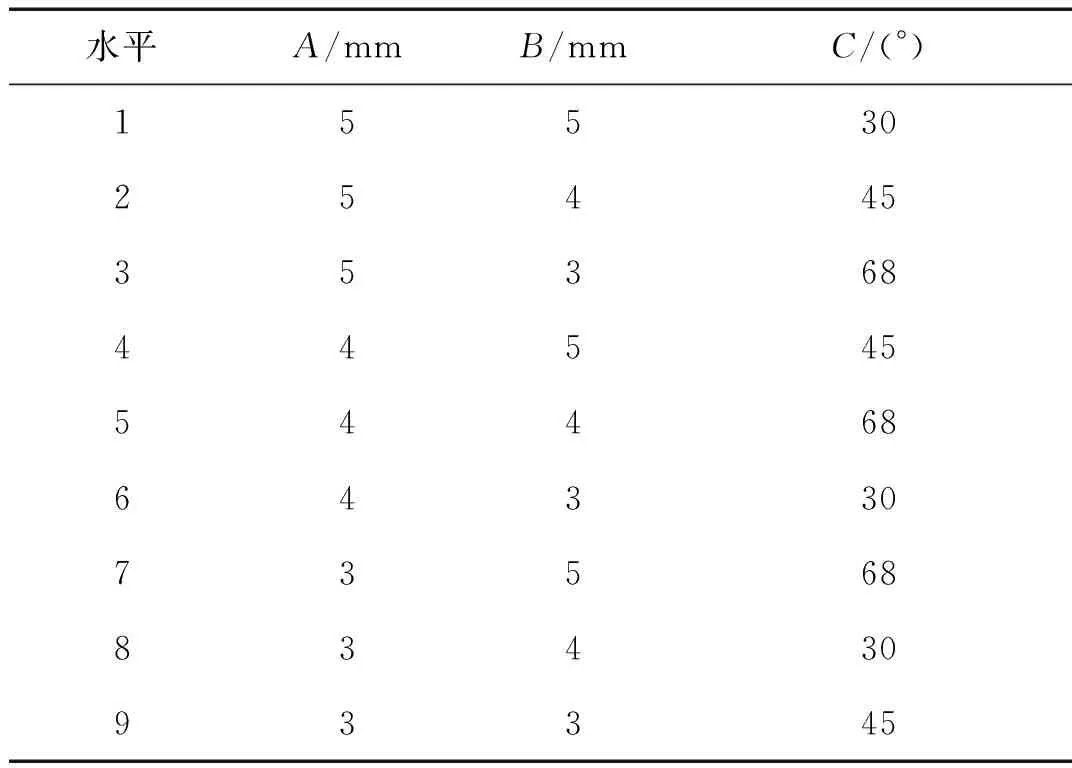
表3 射流侵彻引爆爆炸反应装甲正交L9(34)试验方案

3 结果分析

3.1 射流特性

图4给出了射流速度空间分布云图。由图4可知，在炸药起爆后33 μs，药型罩被爆轰波完全压垮形成射流，射流拉伸，头部到达距离药型罩100 mm位置处。此时射流头部速度约6 274 m/s，杵体部分的最小速度约为336.2 m/s。图5给出了33 μs时刻射流的三维形貌及60 mm的有效长度(射流微元速度大于2 000 m/s)，有效长度的射流平均直径4 mm。

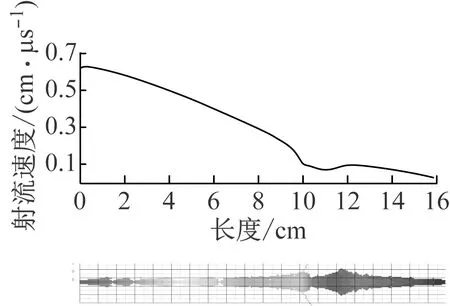
图4 T=33 μs时射流速度分布曲线

图5 T=33 μs时射流有效长度

3.2 飞板飞散及对射流干扰特性

为评估爆炸反应装甲对射流的干扰效率，本文确定受扰后侵彻质量微元离开轴线所获横向动量值、头部侵彻质量微元平均速度值及射流穿透整个靶板时间值作为射流受干扰效率的评估指标，分别记为：M、V和T。

针对表3试验方案中9个试验号进行数值模拟，对数值试验结果进行综合比较，比较鉴别3个影响因素对评估射流3个评价指标的影响程度，从而获得爆炸反应装甲对射流的影响规律。

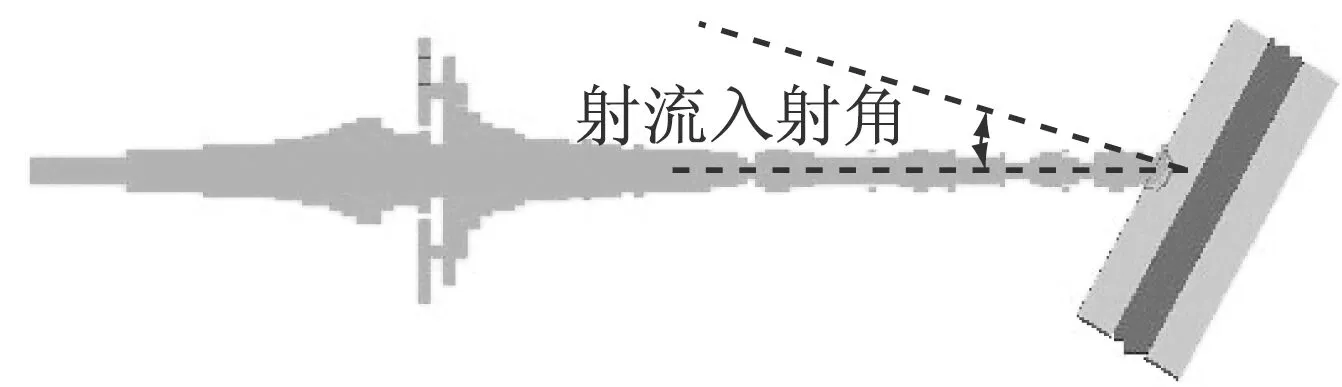
图6 射流入射角

所有试验号的反应装甲均取3个放置角度，即射流入射角分别为：30°、45°、68°，图6给出了射流入射角的定义。如图7所示，是5/5/5型(即：前、后飞板和夹层装药的厚度均为5 mm)爆炸反应装甲3个不同角度放置工况。

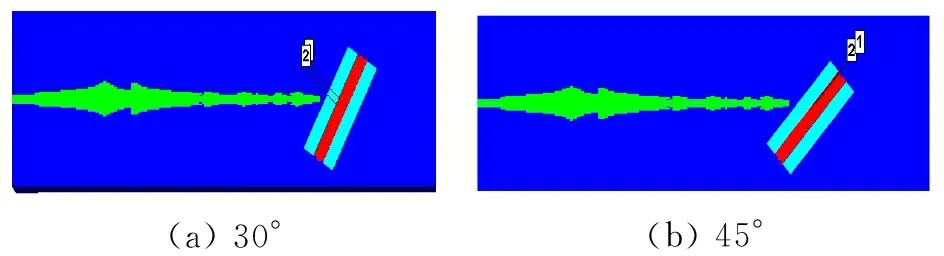
(a)30°(b)45°

(c) 68°

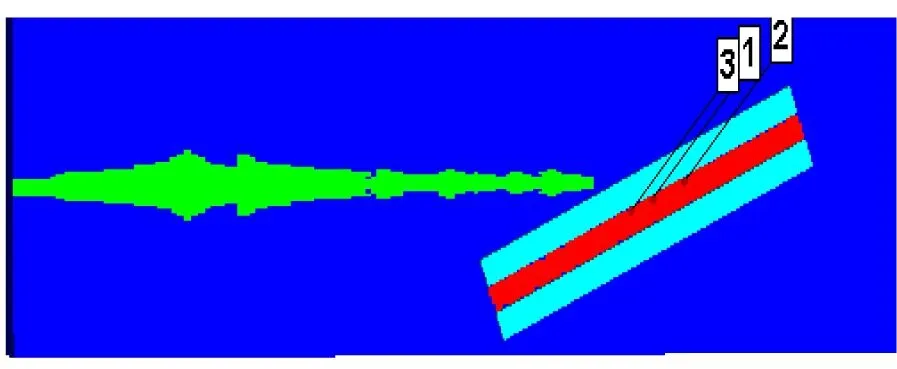
模拟过程中，通过夹层炸药中预设的高斯点提取冲击起爆压力，判别冲击压力峰值是否达到Comp.B炸药的冲击起爆阈值。图8中的高斯点压力时程曲线显示，夹层装药中冲击压力峰值均超过Comp.B炸药冲击起爆压力阈值[12]—7 GPa，表明30°、45°、68°放置的5/5/5型爆炸反应装甲将被顺利起爆。同时，从夹层装药的反应率也可判别炸药是否被高速射流正常冲击起爆，图9给出了5/5/5型爆炸应装甲45°夹角放置时，夹层装药爆轰反应率随时间变化云图，云纹图显示绝大部分夹层装药在6.8 μs时刻完成爆轰反应，表明夹层装药被射流顺利冲击起爆。

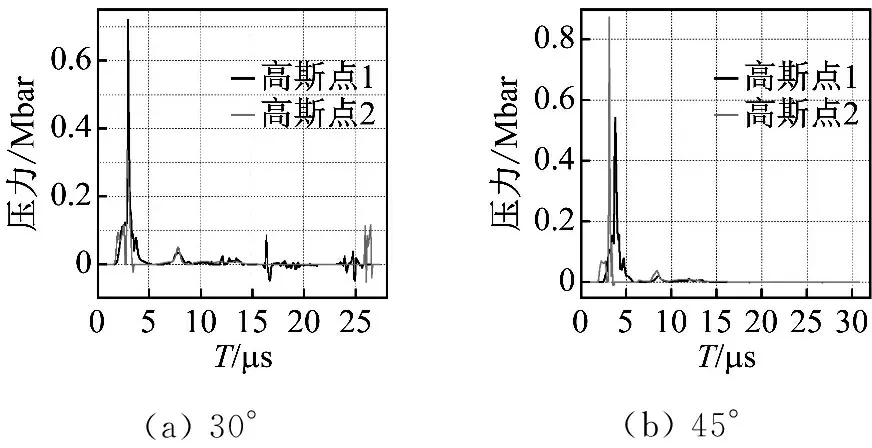
(a)30°(b)45°

(c) 68°

(a)T=3.4μs(b)T=4.4μs

(c) T=6.8 μs

图10给出5/5/5型反爆炸应装甲45°放置时，不同时刻面板、背板运动切割射流的模拟结果。由图10可知，当平面夹层装药被射流冲击引爆后，爆轰产物迅速向外膨胀，随着爆轰反应的继续增长，驱动面、背板沿着各自法线方向飞散。10 μs时，射流穿透了面板、夹层装药和背板，在反应装甲中形成初始穿孔，此时夹层装药已经被完全引爆，飞板开始变形。射流头部在侵彻过程中会有一部分被侵蚀，射流速度也随之下降，头部明显变粗。在这一阶段，射流径向并未与飞板发生明显作用，因此，在射流侵彻形成的通道内，射流可以无阻碍的通过。16 μs时，可以明显看到背板和面板发生严重变形，经爆轰压力驱动获得速度的飞板开始对射流横向切割，被切割的射流段直径发生径缩变小，进一步拉伸出“波浪”形态，射流质量微元获得横向动量。26 μs时，受到飞板切割干扰的射流段已经发生了明显大变形，飞板持续和射流碰撞，射流拉伸断裂，直至完全被切断。

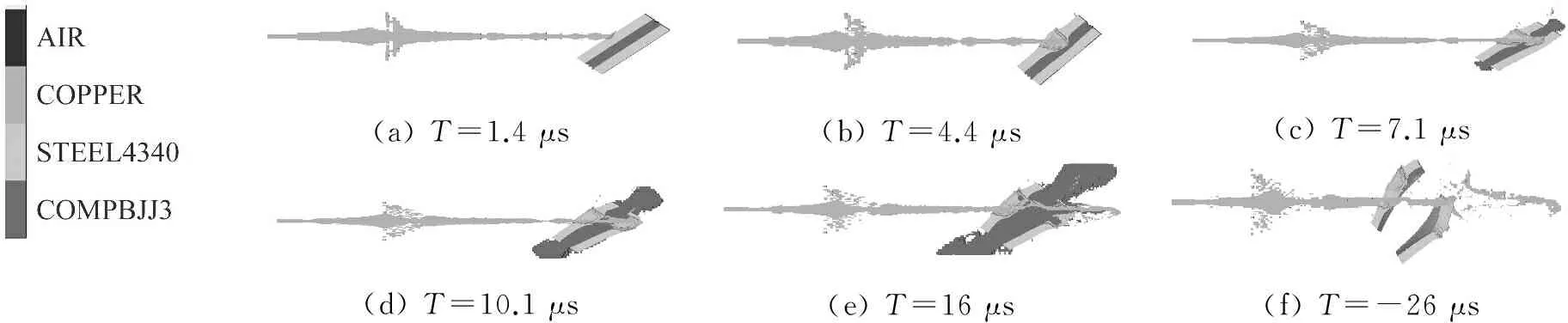
(a)T=1.4μs(b)T=4.4μs(c)T=7.1μs(d)T=10.1μs(e)T=16μs(f)T=-26μs

图10 5/5/5型爆炸反应装甲45°放置飞板切割射流

Fig.10 Typical status of flyer plate incise jet 45°5/5/5 ERA

随时间的演化，飞板继续对后续射流进行切割干扰，直至面板、背板完全飞离轴线，飞板与射流相互作用结束，后续射流可以无障碍继续通过。

面板和背板有相似的运动规律，夹层装药被射流引爆，爆轰压力开始驱动飞板加速，飞板横向(垂直射流轴线方向)速度变化曲线，如图11所示。在爆轰初始阶段，面板、背板的加速度很大，运动速度快速增加，但随着时间的推进，爆轰产物剧烈膨胀导致爆轰产物压力迅速衰减，致使飞板加速度渐趋于0，运动速度的增长越来越小，最终趋于一个稳定的值。

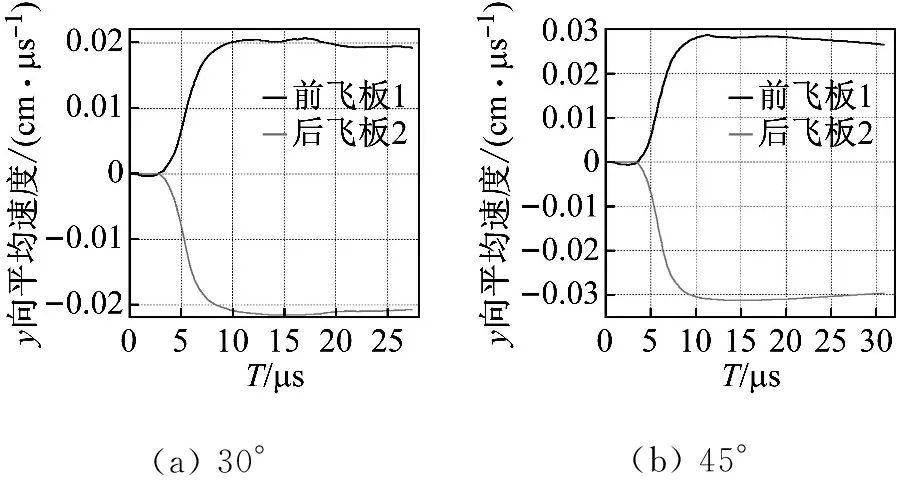
(a)30°(b)45°

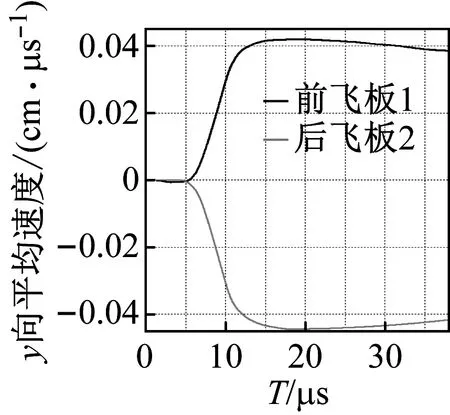
(c) 68°

3.3 射流干扰的正交采样统计分析

针对表3中各试验号的模拟结果，采用正交数值试验的数据分析方法和统计模型，对三个影响因素开展统计分析，数值试验模拟结果，如表4、表5所示。

基于正交试验的极差分析法对表3中所有试验号的评估指标数值结果进行极差统计分析。表4中，“评估指标”列是数值试验值。随时间演化，射流横向动量、头部速度会随时间变化，为确保模拟结果在时间上有可比性，表4中射流横向动量M、射流头部速度V均取各试验号射流侵彻反应装甲10 μs时刻平均值，指标T取射流穿透背板的时间值。

表4 射流侵彻引爆爆炸反应装甲数值试验结果

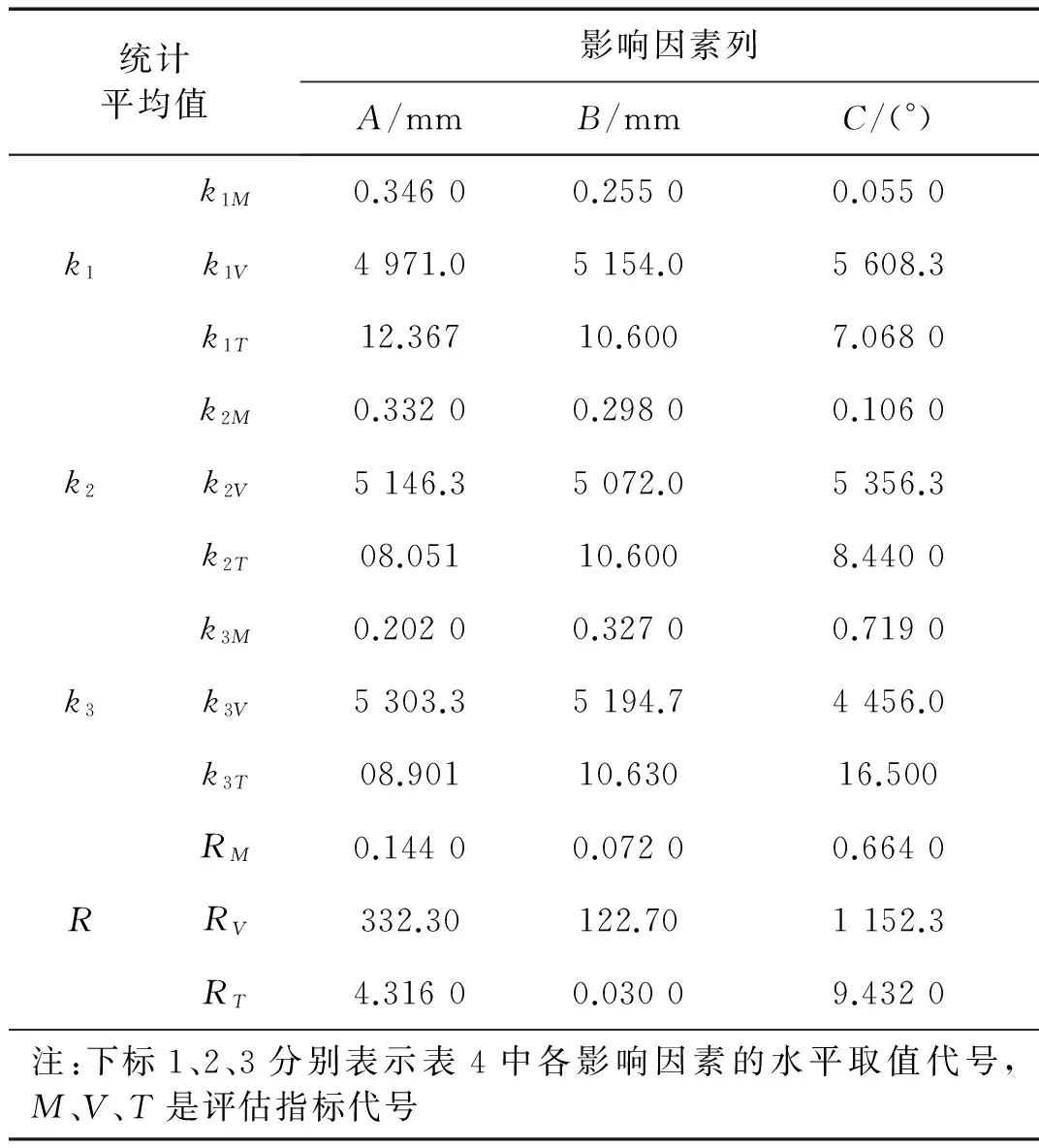
表5 射流侵彻引爆爆炸反应装甲评估指标的统计分析结果

侵彻引爆中，各因素对反应装甲干扰射流效率的评估指标影响具有一定的主次关系。某一因素对评估指标影响大、是主要的，那这个因素诸水平相应的指标值之间的差异就大；反之，该因素诸水平相应的指标值之间的差异就小，其主次关系用极差R来表示。

表5中k1、k2和k3是统计平均值，用于求各影响因数的极差R。各个因素列级差R的大小，反应了该列所排因素选取的水平变动对评估指标的影响大小。由表5的RM行可知，A、B、C3个因素的极差分别为0.144、0.072、0.644，由极差大小可以排出各因素的主次：C>A>B。由此可判断入射角对射流横向动量的获得影响最大，是主要影响因素，夹层装药厚度的影响相对较小，从极差值的大小可以看出，入射角对射流横向动量的影响是夹层装药厚度影响的9倍，是飞板厚度影响的4～5倍。

根据三影响因素下表5的RV行射流头部平均速度极差R大小，可以排出各因素的主次：C>A>B。其中C列的射流入射角因素极差R最大，达到1 152.3，A列的飞板厚度影响因素是第二大影响因素，B列的夹层装药厚度影响因数极差值最小，R=122.7。且从表4的指标列中射流头部速度值可观察到，随着入射角度的增加，射流头部速度大幅降低。该结果表明入射角是射流侵彻爆炸反应装甲时，导致头部速度变化的最大影响因素，第二主要影响因素是爆炸反应装甲的飞板厚度，而夹层装药厚度对射流头部速度的影响相对较小。入射角对射流头部速度的影响是夹层装药厚度影响的9倍，是飞板厚度影响的3倍多。

同理，观察RT的极差R值可知各因素的主次：C>A>B，入射角对射流穿透爆炸反应装甲背板时间影响最大，极差R值9.432，同时表4指标V列中值显示穿透背板时间随着入射角的增大而增大。爆炸反应装甲飞板厚度影响次之，极差R值为4.316，夹层装药厚度影响相对较小，极差R值仅为0.03。入射角对射流穿透背板时间的影响是夹层装药厚度影响的314倍，是飞板厚度影响的2倍。

为直观起见，将因素水平作横坐标，三个评价指标横向动量M、头部速度V及穿透靶板时间T作纵坐标，作出指标—因素关系图。

由图12可知，在本研究中计算设定的三个因素变化范围内，各因素对射流的干扰影响程度有较大差异。入射角(影响因素C)对射流干扰的三个评价指标影响曲线较为陡直，曲线上升较快，呈单调递增趋势，且幅值变化较大，表明随着入射角的增大，反应装甲对射流的干扰效率越高，射流侵彻爆炸反应装甲对入射角最为敏感，是最大的影响因素，该结论与文献[4]的数值模拟结果及试验得出的结论相符合。

爆炸反应装甲的飞板厚度(影响因素A)对三个射流干扰的评价指标都有较大干扰，特别对射流穿透飞板的时间影响较大，影响曲线变化相对剧烈，是除入射角外，最主要的影响因素之一。

夹层装药厚度(影响因素B)的影响曲线在三个评价指标中都相对平缓，对射流的干扰影响相对较小，从图12(c)可以观察到夹层装药厚度影响因素曲线近似水平直线，表明B因数对射流穿透背板时间无显著影响。

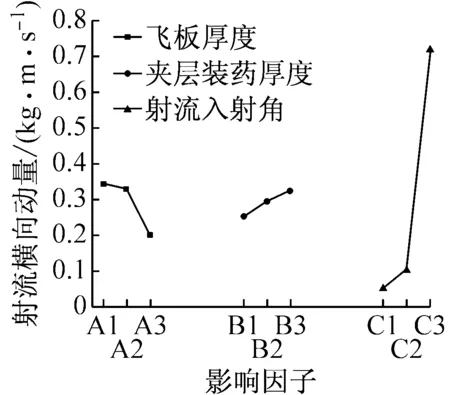
(a) 横向动量趋势

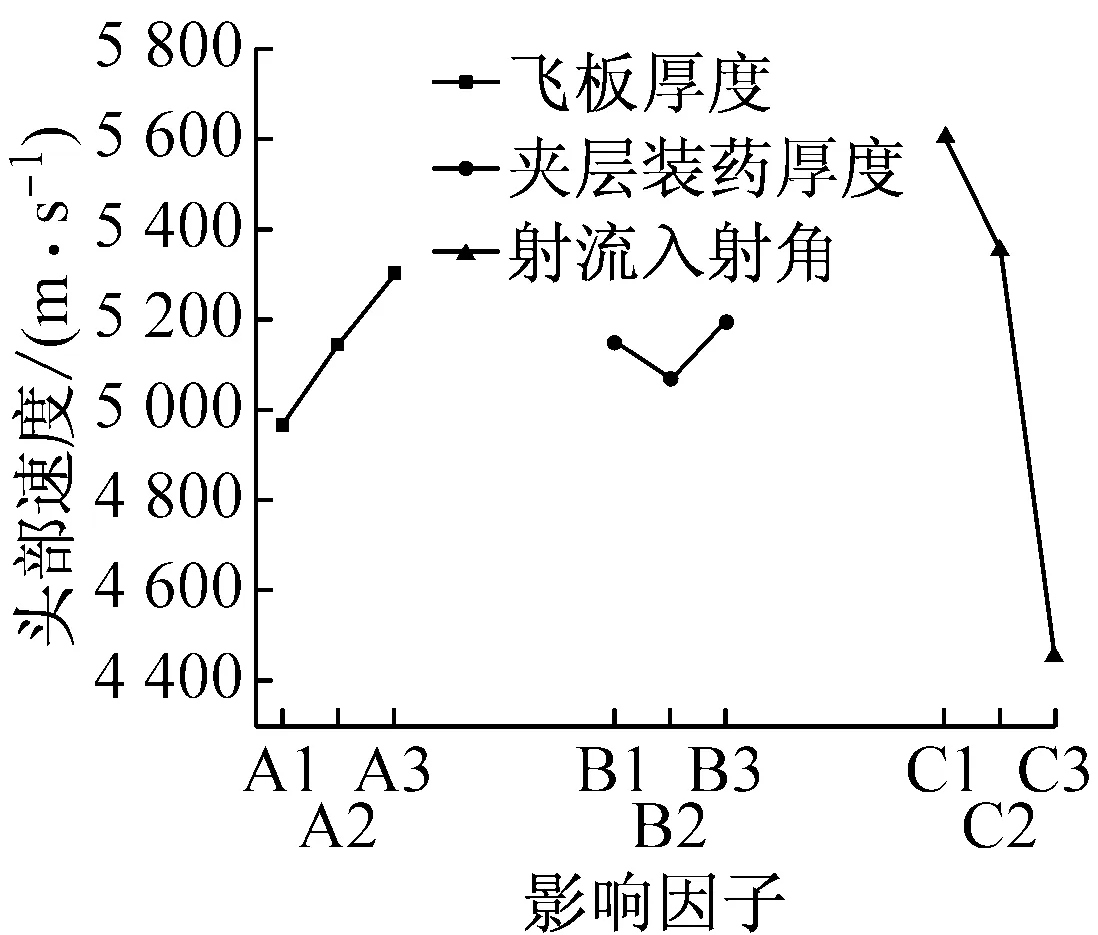
(b) 头部速度趋势

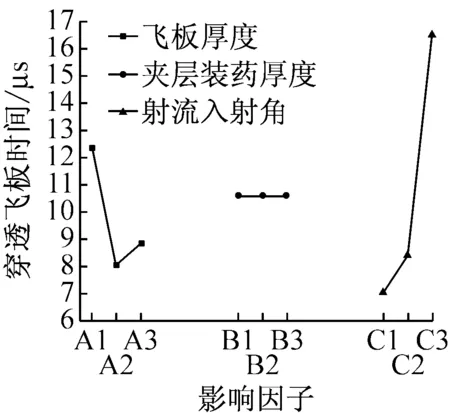
(c) 穿透时间趋势

4 结 论

(1) 入射角度对射流干扰效率的评价指标横向动量、头部速度及穿透背板时间均具有显著性的影响，是最主要的影响因素。射流横向动量、穿透背板时间随入射角的增大具有最大的增加速率，头部速度随入射角的增大下降最快。入射角对射流横向动量的影响是夹层装药厚度影响的9倍，飞板厚度影响的4～5倍；对射流头部速度的影响是夹层装药厚度影响的9倍，飞板厚度影响的3倍多；对射流穿透背板时间的影响是夹层装药厚度影响的314倍，飞板厚度影响的2倍。

(2) 飞板厚度对射流干扰效率的评价指标均有较大的影响，是主要影响因素之一。随飞板厚度增加，射流横向动量、穿透背板时间均有较大的增加，呈正相关关系；头部速度有较快的下降趋势，呈负相关关系。夹层装药厚度因素和射流横向动量呈较明显的正相关趋势，对射流头部速度影响无明显规律性，对射流穿透背板时间无显著影响。

(3) 射流受飞板切割获得横向动量后，导致射流在进一步的侵彻拉伸过程中更容易断裂，这将大幅降低射流后续的侵彻威力。

[1] 黄正祥. 聚能装药理论与实践[M]. 北京：北京理工大学出版社，2014.

[2] CHEN Meiling, YANG Lidong, SHEN Xiaojun, et al. The design of small-calibre tandem warhead against tank withreactive armour[C]∥19th International Symposium of Ballistics. Interlaken: Casino Kursaal Congress Center, 2001:691-695.

[3] MAYSELLESS M, ERLICH Y, FALCOVITZ Y, et al. Interaction of shaped charge jets with reactive armor[C]∥8th Interna-tional Symposium on Ballistics. Orlando:[s.n.],1984.

[4] 武海军，陈利，王江波，等. 反应装甲对射流干扰的数值模拟研究[J]. 北京理工大学学报，2006，26(7)：565-568.

WU Haijun, CHEN Li, WANG Jiangbo, et al. Numerical simulation on reactive armor disturbing jet[J]. Transactions of Beijing Institute of Technology, 2006，26(7)：565-568.

[5] 吴成，蒋建伟，冯顺山，等. 爆炸反应装甲运动规律的数值仿真及研究[J]. 兵工学报，2002，23(1)：35-38.

WU Cheng, JIANG Jianwei, FENG Shunshan, et al. A study on the moving features of explosive reactive armor by numerical simulation and experiments[J]. Acta Armamentarii, 2002，23(1)：35-38.

[6] 曾凡君，李健，梁秀清，等. 反应装甲爆轰阶段对射流干扰机理的研究[J]. 北京理工大学学报，1994(3)：286-291.

ZENG Fanjun, Li Jian, LIANG Xiuqing, et al. A further study of the disturbance mechanism on jets caused by reactive armors[J]. Transactions of Beijing Institute of Technology, 1994(3)：286-291.

[7] 黄正祥，徐学华，陈惠武. 聚能射流对陶瓷装甲侵彻深度灰色预估[J]. 弹箭与制导学报，2004,24(4)：31-33.

HUANG Zhengxiang, XU Xuehua, CHEN Huiwu. The penetrating depth grey prediction of cumulative jet on ceramic armor[J]. Journal of Projectiles, Rockets,Missiles and Guidance, 2004,24(4):31-33.

[8] 李磊，马宏昊，沈兆武. 基于正交设计方法的双锥罩结构优化设计[J]. 爆炸与冲击，2013, 33(6):567-573.

LI Lei, MA Honghao, SHEN Zhaowu. Optimal design of biconical liner structure based on orthogonal design method[J]. Explosion and Shock Waves, 2013,33(6):567-573.

[9] AUTODYN users manual[M].California:Century Dynamics Corporation,2005.

[10] 沈飞，王辉，袁建飞. 一种确定JWL状态方程参数的简易算法[J]. 振动与冲击，2014,33(9)：107-110.

SHEN Fei, WANG Hui, YUAN Jianfei. A simple method for determining parameters of JWL EOS[J]. Journal of Vibration and Shock, 2014,33(9)：107-110.

[11] CHEN J K, CHING H K, ALLAHDADI F A. Shock-induced detonation of high explosives by high velocity impact[J]. Journal of Mechanics of Materials and Structures,2007,2(9):1701-1721.

[12] 梁斌，冯高鹏，魏雪婷. 多枚破片冲击引爆带盖板炸药数值模拟分析[J]. 弹箭与制导学报，2013，33(6):63-69.

LIANG Bin, FENG Gaopeng, WEI Xueting. Numerical simulation on shock initiation of composition B explosive subjected to multi-fragment[J]. Journal of Projectiles, Rockets,Missiles and Guidance, 2013,33(6):63-69.

[13] 刘振学，王力. 实验设计与数据处理[M]. 北京，化学工业出版社，2015.

[14] 刘达民，陈岩.应用统计[M]. 北京：化学工业出版社,2004.

[15] 雷正保，余进修，颜海棋，等. 基于正交试验设计的间断式砼护栏研究[J]. 振动与冲击，2007，26(7)：13-17.

LEI Zhengbao, YU Jinxiu, YAN Haiqi, et al. Research on interrupted type of concrete guardralls using orthogonal design[J]. Journal of Vibration and Shock, 2007，26(7)：13-17.

Parametric sensitivity of explosive reactive armor disturbance jet based on orthogonal numerical tests

BAI Yunshan, FENG Xiaowei, LIANG Bin, FENG Gaopeng

(Institute of Systems of Engineering, China Academy of Engineering Physics, Mianyang 621900, China)

Based on the shock initiation of explosive—Lee-Tarver ignition and growth model, a three-dimensional numerical model was developed using the finite difference code AUTODYN to simulate the processes of jet penetrating and detonating a “sandwich” ERA(explosive reactive armor), and an explosive pressure driven flyer plate incising a jet. Aiming at three influence factors in-cluding flyer plate thickness, interlayer charge thickness and jet inclined angle, the evaluating indicators of jet disturbing efficiency were determined. By means of the orthogonal statistical test method, the parametric sensitivity of the evaluating indicators of jet disturbing efficiency was studied. Results demonstrated that jet inclined angle is the main influence factor, jet’s lateral momentum,jet tip velocity and the time of jet penetrating back plate are significantly affected by jet inclined angle, the relationship between jet inclined angle and evaluating indicators is positively correlated; flyer plate thickness is the second main influence factors, it affects all evaluating indicators evidently; interlayer charge thickness’s influence on jet tip velocity has no obvious regularity, and has also few influence on the time of jet penetrating back plate.

mechanics of explosion; reactive armor; orthogonal design; evaluation indicator; AUTODYN software

国家自然科学青年基金项目(11502258)；中国工程物理研究院发展基金(2014B0101009)

2015-12-08 修改稿收到日期：2016-03-01

拜云山 男，硕士，工程师，1983年生

冯晓伟 男，博士，副研究员，1984年生

TJ414.+2

A

10.13465/j.cnki.jvs.2017.09.014