寻求平面图形面积教学的最佳路径

杨红梅

平面图形的面积教学有合情想象、演绎推导、精确计算，也离不开学生的感知、探索、推理。几何图形较为抽象，教师可以引导学生借助生活经验、知识背景，变抽象为直观，在观察、实验、猜想等探索环节中知识得以扩展延伸，体会到学习数学的乐趣。如果教师忽视了学生探索的过程，片面追求结果，“快捷”地将公式告知学生，会将学生陷于被动接受的境地。小学平面图形的面积涉及三角形、矩形、平行四边形、梯形、圆的面积，教师要针对不同时期学生的知识背景，采用不同的方式引导学生推导面积公式。

一、以“割补”探究平行四边形的面积

1.以猜想代替灌输。传统教学中，教师让学生记忆“平行四边形的面积＝底×高”的结论，或机械讲解推导过程，忽视了学生合情推理能力的培养，学生的求异思维能力难有发展。教师要培养学生科学探究的能力，要让他们乐于思考、乐于猜想。教师呈现长6米、宽4米的长方形以及底边长6米、高4米的平行四边形的花坛，提出问题：“用什么方法知道平行四边形花坛的面积？”学生在网络中画出两个图形，用数格子的方法求出平行四边形的面积。学生比较后发现两个图形相等，且等底等高，随后提出猜想：平行四边形的面积是底×高。

2.验证不满足于预设。平行四边形要割补成长方形，教师习惯于将平行四边形割成“三角形+梯形”，再补成长方形（如图一）。当学生的思维与教师的预设不一致，教师就会通过“强拽”的方式，让学生的思维进入“正轨”。这种方法显然是不可取的，教师要放手让学生剪、拼，就会形成多种不同的方法，有学生将平行四边形剪成两个梯形，再拼成长方形（如图二）；有学生各剪去一个小三角形，再拼成长方形（如图三）。

图一

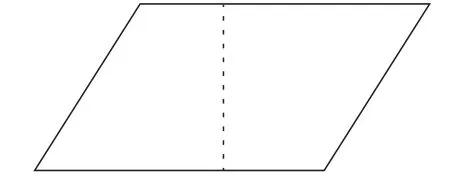
图二

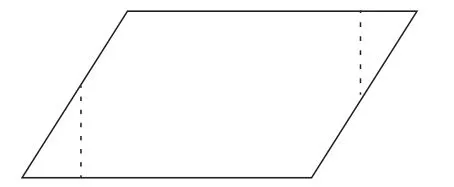
图三

二、以转化探究三角形的面积

学生已具备将平行四边形转化为长方形的基础，可以利用手中的学具，以割补、剪拼等手段将三角形转化为平行四边形。教师让学生运用数方格的方法猜一猜三角形的面积是多少，以小组为单位开展探究，拿出事先准备好的三角形进行割补、剪拼等操作，将三角形的面积转化为熟悉的图形面积。学生将手中的两个完全一样的三角形拼成了各种各样的四边形，有学生将两个同样的直角三角形拼成了一个长方形，有学生将直角三角形拼成了一个平行四边形，有学生将两个钝角三角形拼成了一个平行四边形……学生虽然拼成的图形不同，但都可以推导出三角形的面积。

三、以史实探究圆的面积

在圆的面积教学中，教师将数学史融入面积教学之中，让学生经历知识的发现过程。教师从“圆形草坪面积”引入，让学生猜测圆的面积与圆的半径、直径或周长之间的关系，有学生说圆的面积是周长的一半乘半径，也就是圆周率乘圆的半径的平方。教师从祖冲之用圆内接多边形面积去逼近圆面积、开普勒将圆分成若干小扇形去推导圆面积，引导学生探究圆的面积与半径之间的关系，将圆转化为长方形，再推导其面积。教师放手让学生探索，学生尝试将圆分成若干等分，通过拼接成一个长方形，在拼的过程发现分的份数越多，拼成的图形就会越接近长方形，长方形的长正好是圆的周长的一半，宽相当于圆的半径r，于是圆的面积公式唾手可得。

总之，在小学平面图形面积教学中，教师要摆脱教材的束缚，引领学生经历观察、操作、想象、分析，在推导的过程中激活思维、提升技能。