温故知新凸显本质——例谈计算类复习课教学

符玲利

复习课是教学中必不可少的，很多教师认为学生要想得高分，必须复习要到位。但是很多教师却将复习课上成“炒冷饭”或“题海战”，令学生对复习课毫无兴趣。尤其是计算课的复习，一味进行重复计算会显得枯燥、乏味，既不能对计算方法有所提升，又不能提高计算的正确率。计算类复习课需要做什么？史宁中指出，教学的最终目标，是要让学习者会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。根据这一终极目标，计算类复习需要教师考虑如何让学生用他们的语言表达计算的方法及算理，使学生知其然（算法），又知其所以然（算理）。即要让学生系统地看知识，发现知识间内在的联系，从而达到理解数学本质的目的。

一、问题分析

1.基础知识掌握得不扎实。算法是解一种类型题所采用的任意一种方法，它是运算中最重要的一部分。但是有些学生课堂上对教师的算法形成过程理解不到位，随着综合能力要求的提高，学生就会出现各种错误。例如，笔者在六年级做的一次计算小调查（如图）：

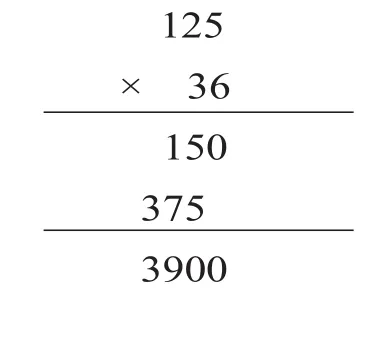
从学生的计算错误来看，学生是运算顺序出错导致的错误。而导致运算顺序出错的根本原因就是对运算顺序的理解不到位，体会不够深刻，一旦外界因素给予干扰，就会出现如：或这样的错误。

2.对运算的算理理解不够。笔者曾对一所民办学校四年级某班的学生进行调查，发现计算准确率均达90%以上，而能大致说出算理的却只有67.39%。学生没有很好地理解乘法运算中数位概念为基础的算理，只停留在机械的纯技术计算水平上这样的结论，计算方法掌握仅是模仿，故导致学生在计算时出现形形色色的错误。

3.感知、记忆不准确。计算时学生的感知参与其中，但常常因为学生的感知水平低，就会出现如59抄成56的错误。记忆也是决定运算正确的要素之一，但知识的保存、更新、积累和提取过程中任何一环出现障碍，就会造成学生计算错误。如右上图1-3，学生对计算法则提取出现错误，就有了各式的错误。如图1为凑整，把101写成了101-1；图2典型的“除法分配律”错误；图3受A-(B+C)=A-B-C的影响，中间又省略了一步，就出现了问题。所以，教师除了需要培养学生养成良好的学习习惯之外，还要尽可能地减少靠纯记忆学习内容，努力让学生在理解的基础上掌握方法，从而达到减轻学业负担的目的。

（图1）

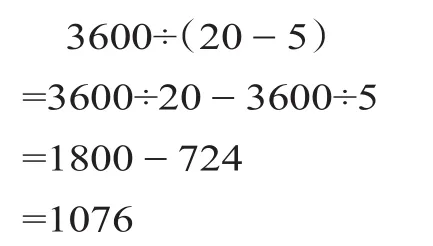
（图2）

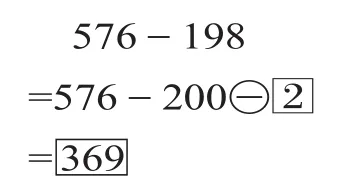
(图3)

二、计算类复习课的有效策略

笔者认为可以从比较、沟通、建模三个方面寻找复习课中的知识联系，突出数学本质，让学生在融会贯通中真正理解其本真意义，从而彻底改正错误，提高学生计算的正确率。

1.在“比较”中明理。在计算复习课中，笔者在调查中发现学生对计算方法已经非常熟练，但也发现学生的计算方法被禁锢。笔者认为，在计算课的复习中，教师要唤醒学生的认知，在比较中掌握多种算法；在比较中深层次理解算理；在比较中明白笔算乘法的本质。以《三位数乘两位数的复习》为例，看看如何用“比较”感悟算理、突显计算的本质：

计算125×12，并说说每一步的算理；出示不同的计算方法，沟通算理。

（1）比较竖式①和竖式②，在计算上有什么不同点吗？学生会有两个层次的理解：一个是先算125×2，另一个是先算125×10。教师概括得出：125×2+125×10=1500。（2）继续比较竖式③和竖式④，计算上有什么共同点吗？学生均能找到共性：算5个12、20个12和100个12的和。12×5+12×20+12×100=1500。（3）比较4道竖式，计算上有什么共同点和不同点？小结：都是把一个数拆成多个数的和，几个百和几个十、几个一的和，这样方便口算和笔算。（4）除了可以这样拆，这道算式还有其他的拆分方法吗？根据数的特点，学生把算式拆分成125×8+125×4或125×6+125×6。通过比较不同的拆法，引导学生得出：拆成整十或整百，方便口算。把12拆成8+4是简便计算，这种方法是运用了以后学习的乘法分配律。

由第一轮和第二轮的比较，学生可以感悟多位数乘法就是求几个几的口算方法，从而打通算理，打破学生固定计算（思维）模式。第三轮的比较，让学生用自己的语言描述对计算竖式的认知，达到用数学语言表达数学世界的目的。第四轮比较让学生感知以后的乘法分配律就是从乘法的意义而来，突出计算教学的数学本质，为后续的学习进行有效铺垫。

2.在“沟通”中融会贯通。

抓住数学知识本源和数学思想方法，能够加深对知识的理解；沟通知识间的内在联系，可以让学生在解决问题的时候举一反三、融会贯通、把握实质。因此，学生在学习的时候，教师判断其对数学的理解能力，主要看是否知道知识的内在联系和抽象的关系，能否形成自己的知识框架，能否做到举一反三。在复习阶段，教师需要帮助学生搭建沟通的平台，让学生的知识形成系统，最后达到熟练掌握，灵活运用的目的。

以计算内容为例：二至四年级乘、除法的教学根据难度不同被分解在多册教材中，但其计算方法有一致性，故经过复习，学生能形成系统的框架。但分数的乘除法计算方法不同，算理不同，内容散而杂，如何才能让学生理解分数乘除法的计算本质，使之形成系统呢？笔者认为，找到分数乘除法、分数加减法的内在联系，才能让学生清晰地认识到这一大块知识的整体性，才能有效帮助学生减轻学习的负担。

以《分数乘除法的复习》为例，课始安排学生计算，然后组织学生进行各类计算方法的沟通。

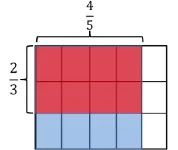
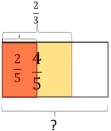
计算时需要先求五分之四的二分之一是多少，再求这样的三份，即：借助图形理解换算的过程，有效降低了理解的难度。

除了这种办法，还可以利用商不变性质进行验证，被除数和除数同时乘除数变成1，商即和被除数相等：

通过对比发现除法计算的共性：即除以一个不为0的数，等于乘以它的倒数。借助数形结合明白为什么要乘以它的倒数，打通了分数除法的算理与算法。

这样的沟通，打通了分数乘整数与分数除以整数计算方法的共性，有效突出了分数乘除整数的计算本质：基于分数单位的整数乘除法。

（4）分数乘除分数的沟通。除了分数除法可以转化成分数乘法来计算外，分数乘法和除法在计算方法上还有什么联系吗？分数乘分数可以分子乘分子，分母乘分母，分数除法也可以用这方法来解决吗？可见分数乘除法在计算方法上是相通的，本质是基于分数单位的整数乘除法运算，只是分数除法用这种方法不方便，故不常用。

（5）分数各类运算方法的沟通。分数加减法先通分，再加减，那么分数乘除法能不能也用通分的方法来计算？学生通过尝试得到：（分子除以分子，分母除以分母），发现也是可以的。讨论得出分数乘除法和加减法均是基于分数单位的个数加减，或是几个几，包含除的运算，所以本质也是相通的。

五次比较、沟通，分别利用数形结合回顾理解算理，沟通同类计算的方法，掌握算法的本质。比较不同类的计算方法，沟通内在联系，突出数学的本质。

3.在“建模”中形成知识网络。数学模型方法的学习能够促进学生深刻领悟数学的应用价值，培养学生数学应用意识和应用数学的基本能力……那么在计算类复习中如何“建模”？如何通过“建模”提高学生的分析、抽象能力？

以四年级三位数乘两位数这一单元中的数量关系复习为例，笔者设计了如下环节：

师：125×12这道算式可以表示什么数量关系？

生：可以表示单价、数量、总价。

生：买一件东西花了125元，买了12件，一共花了1500元。

生：可以表示速度、时间和路程。

生：每分钟125米，12就是12分钟，1500就是走了1500米。

师：除了表示这两个数量关系以外，还可以表示什么？

生：每天修路125米。

像这样，每天、每小时、每件，表示一份的量，在数学上叫做每份数。那么12天、12小时、12件表示有12份的叫做份数。每份数×份数＝总数。笔者认为,在复习数量关系时，有必要让学生感受到只要是表示一份的量都可以叫做每份数，所有表示几份的数都可以用份数来表示。这样就可以把零散的、不相关的数量关系整合成一条数量关系：每份数×份数＝总数。这样既减轻了学生的记忆负担，又举一反三，为以后学习工作效率、工作时间等数量关系作铺垫，为学生解决各类关于几个几的问题打通要塞。

总之，基于数学本质的计算复习教学，不是简单整理学了什么、错了什么，更不是题海战术、纠纠错，而是要通过有效的方式帮助学生整理学过的知识，找到知识点间的联系，把零散的知识串通，变成系统的知识网络，经历知识由厚变薄的过程，把握计算的数学本质，从而达到灵活运用，巧妙计算，变式创新。