药型罩材料本构模型对EFP数值模拟的影响
2017-05-03冯江拓李芮宇谢海涛马明辉孙宇新
冯江拓, 李芮宇, 周 玲, 谢海涛, 马明辉, 孙宇新
(1 南京理工大学瞬态物理国家重点实验室, 南京 210094; 2 中国兵器科学研究院, 北京 100081;3 北方华安工业集团有限公司, 黑龙江齐齐哈尔 161046)
0 引言
爆炸成型弹丸(EFP)广泛用于串联战斗部对深层工事的前级开坑,或用于攻击装甲车辆和舰船密闭舱等目标。EFP药型罩主要有球缺形药型罩和锥形药型罩,球缺罩EFP相对于同尺寸锥形罩EFP,其稳定飞行速度较低(2 000~3 000 m/s),而弹径较大[1]。随着计算机技术的发展,数值模拟已经成为EFP的重要研究手段。常向阳[2]等使用ALE算法,采用J-C本构模型,模拟了EFP成型及侵彻靶板的过程,但未考虑壳体对EFP成型过程的影响;桂毓林[3]等使用Lagrange算法,采用Steinberg材料本构模型描述药型罩材料,成功对带尾翼的翻转型EFP的成型过程进行了三维数值模拟仿真;蒋建伟[4]采用J-C本构模型描述,模拟了结构参数对有铝壳体的球缺形药型罩EFP成型的影响。
文中使用Autodyn软件,分别使用J-C本构模型和Steinberg本构模型描述药型罩材料,对有钢壳体的110 mm口径球缺形药型罩EFP开展数值模对比研究,拟结合试验,通过分析比较EFP成型、侵彻过程中的变形图像,选择一种适合该类型EFP数值模拟使用的材料本构模型。
1 模型及材料
1.1 计算模型
图1为文中模拟所使用的计算模型:紫铜药型罩曲率半径R=100 mm,厚4 mm;壳体材料为某低碳钢,厚度δ=7.5 mm;B炸药装药直径D=110 mm,高度H=85 mm。靶板为140 mm厚,半径为250 mm的圆柱形靶板,EFP装置距离靶板500 mm。
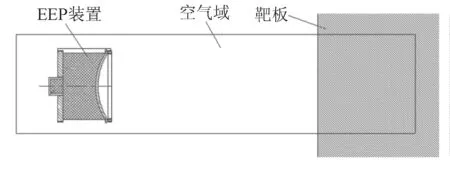
图1 计算模型
采用AUTODYN-2D前处理程序建立二维轴对称模型,空气、炸药和药型罩采用Euler算法,壳体及靶板采用Lagrange算法,通过流固耦合方法实现EFP和靶板之间的作用;对靶板施加无反射边界,靶板与弹丸接触范围内的网格加密;起爆方式为中心面起爆,起爆半径12 mm;炸高500 mm,单位制为mm-mg-ms。
1.2 材料模型
1.2.1 药型罩材料模型
在冲击动力学计算中,由于环境压力很大,材料的应力应变描述为球量部分和偏量部分[5],即所谓流体弹塑性模型,用本构方程描述偏应力和偏应变之间的关系,并用状态方程表达应力张量的球张量部分、能量和密度之间的关系。在对比计算中,EFP的药型罩本构方程分别用J-C本构模型和Steinberg本构模型;而状态方程选用Gruneisen状态方程。
a)J-C本构模型
J-C本构模型[6]使用下式描述材料的屈服应力:
(1)
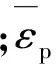
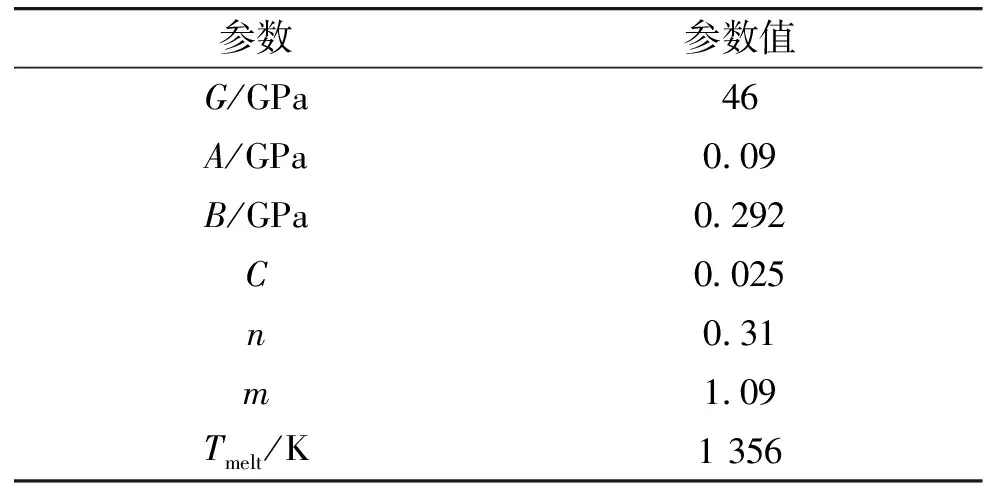
表1 J-C本构模型计算参数
b)Steinberg本构模型
Steinberg本构模型[7]剪切模量和屈服应力的表达式为:
(2)
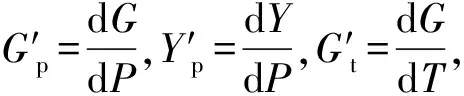
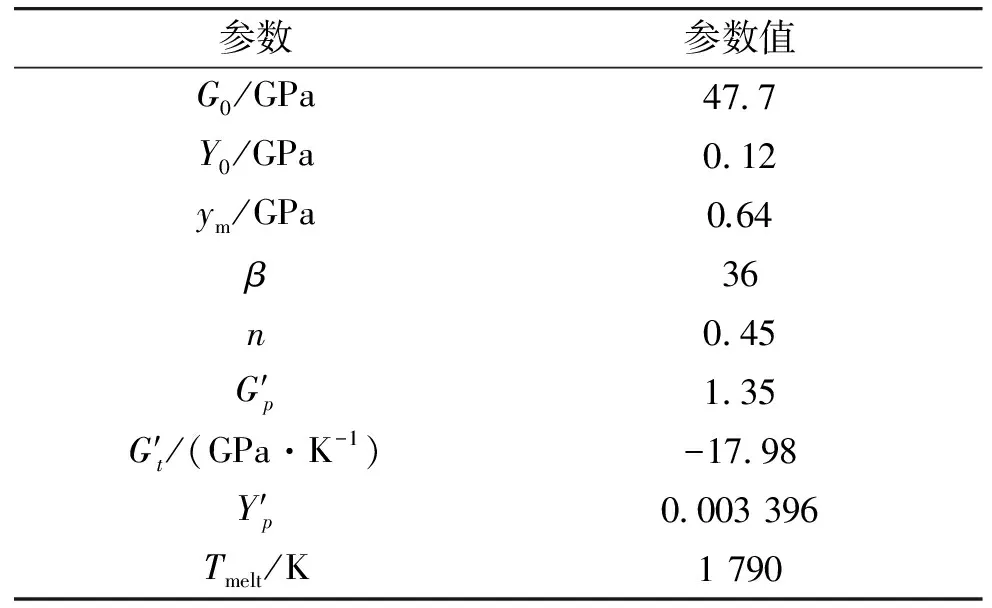
表2 Steinberg本构模型计算参数
1.2.2 其余材料模型及参数
计算中选用的炸药类型为B混合炸药,材料模型为高能炸药爆轰模型,状态方程为JWL状态方程[8],参数见表3。壳体及靶板的屈服强度分别为1.54 GPa和0.42 GPa,材料模型均为J-C本构模型,状态方程选用Gruneisen状态方程。
2 数值模拟结果
2.1 EFP成型过程
2.1.1 药型罩材料选取Steinberg本构方程
表3为EFP成型过程中的头尾速度,由表3看出,在0.008~0.036 ms阶段,由于爆轰驱动,弹丸速度迅速提高:头部速度提高到2 786 m/s,尾部速度也提高到1 947 m/s,头尾速度差值为839 m/s。0.036 ms后,爆轰产物压力下降,弹丸加速缓慢。由于材料内部的速度梯度,头部速度开始下降,尾部速度上升,头尾速度差减少,在0.212 ms时头部速度下降为2 251 m/s,尾部速度上升为2 001 m/s,头尾速度差下降到250 m/s,而此时,弹丸头部飞行距离已经达到炸高,表明从药型罩开始变形到弹丸成型开始侵彻靶板,弹丸头尾速度差一直存在。
图2为EFP成型总体加速度时程曲线,时间起始点为爆轰开始时刻,在0.008~0.014 ms阶段,EFP加速度迅速提高,表明在0.008 ms时刻爆轰波到达药型罩中部,随后滑移至药型罩边缘,并且在爆轰产物压力未显著降低前,一边迫使药型罩变形翻转,一边驱动药型罩材料加速运动;而在0.014~0.030 ms阶段,药型罩加速度下降,表明爆轰产物压力下降;当超过0.030 ms,药型罩加速度减少到近似0,可以认为此后阶段药型罩(EFP)不受爆轰力的作用,药型罩的变形是材料内部的速度梯度引起的。
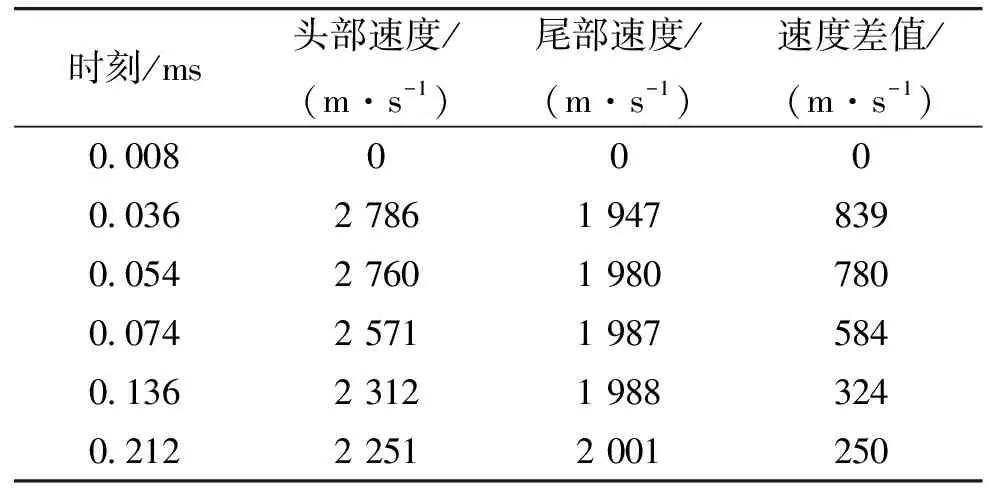
表3 Steinberg本构对应EFP成型过程头尾速度值
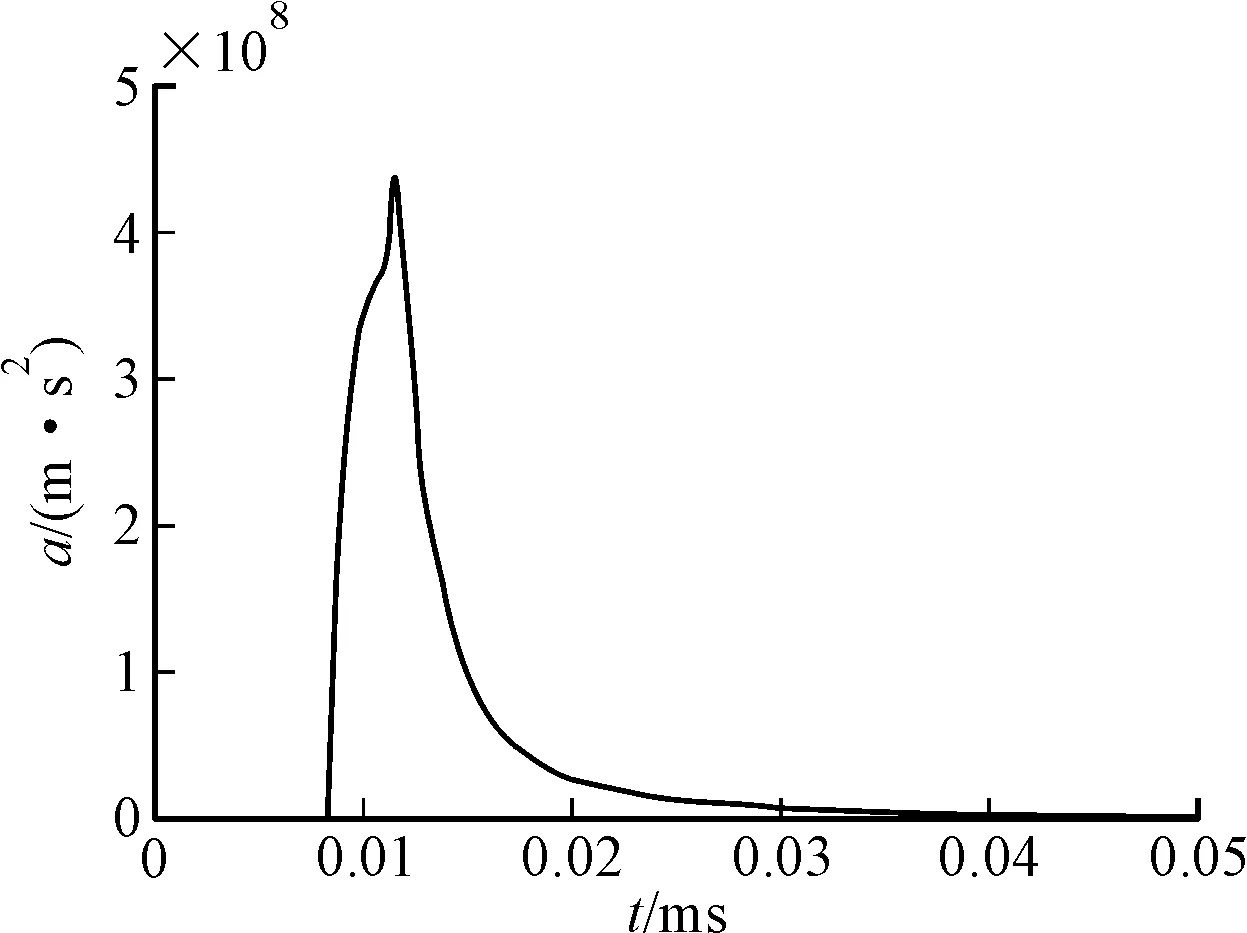
图2 药型罩Steinberg本构模型EFP成型加速度时程
图3为EFP成型过程3个典型时刻的塑性应变分布,在0.074 ms、0.136 ms和0.212 ms时尾部材料塑性应变分别为5.6E+7、3.7E+7和2.8E+7。实际球缺药型罩EFP形成是不可能出现如此大的变形,不符合物理规律;且如此大的应变意味着,在EFP成型过程,塑性功将生成大量热,温度上升至材料熔点,导致屈服应力和剪切模量均接近零。
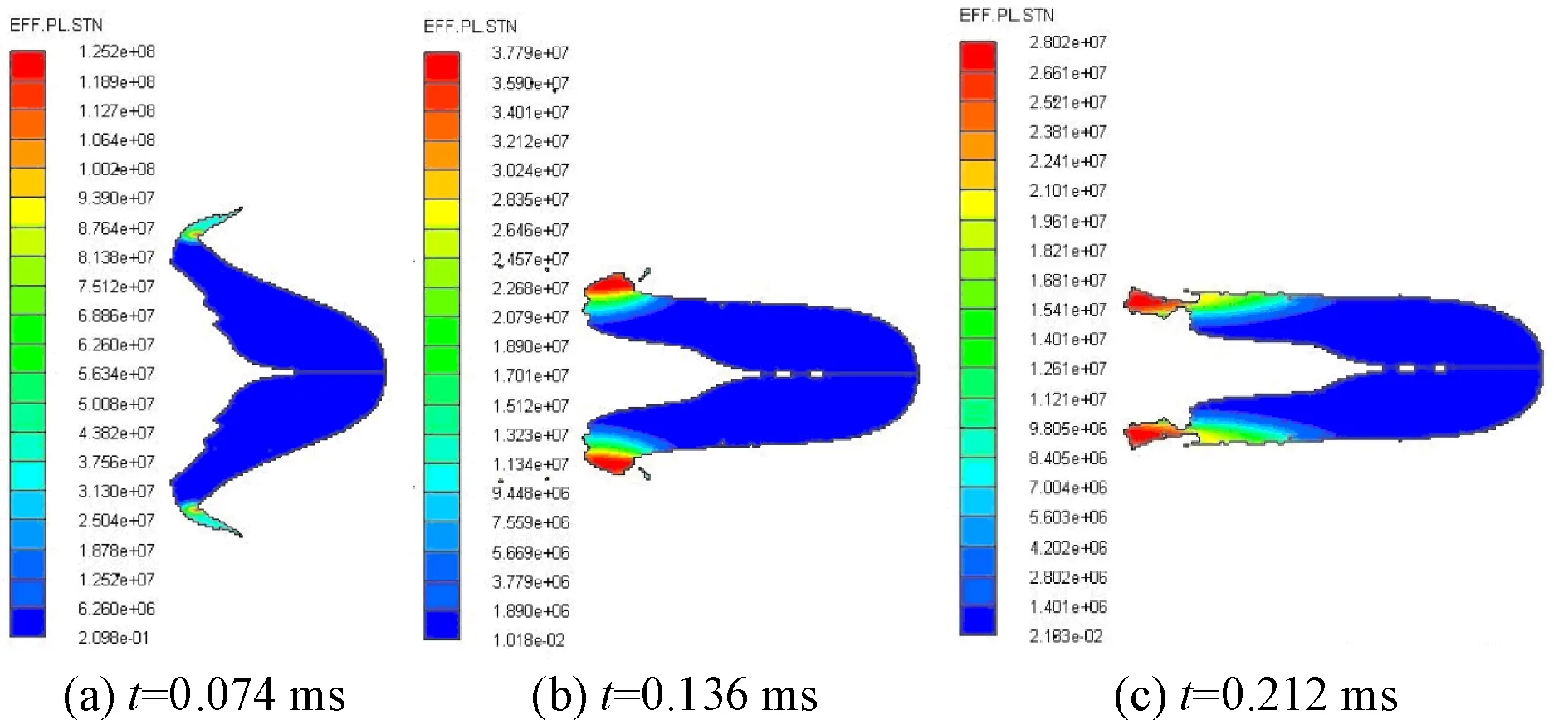
图3 药型罩Steinberg本构模型EFP成型等效塑性应变分布
图4为EFP成型过程3个典型时刻的压力分布云图。弹丸尾部区域显示,在t=0.136 ms时,材料内部压力为150 MPa;在t=0.212 ms时,压力下降到50 MPa以下。在此时,出现尾部部分材料与弹丸主体分离,这主要是材料Steinberg本构方程显示强度与所受压力线性正相关,所以当承受压力从150 MPa下降到50 MPa,材料表现的强度下降,对发生的变形抵抗较差,EFP尾部材料出现断裂。
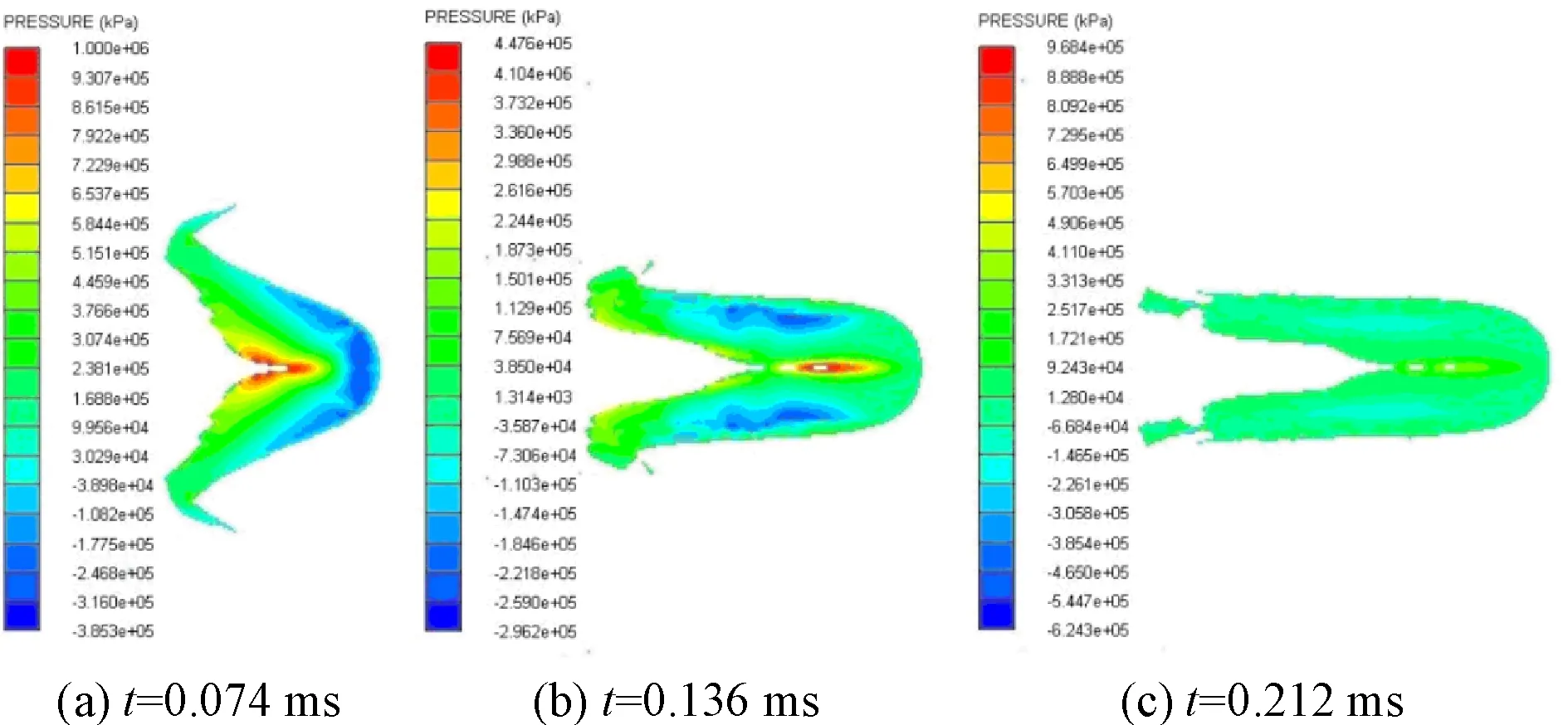
图4 药型罩Steinberg本构模型EFP成型压力分布
参考文献[1,3]给出的试验照片显示,紫铜材质球缺型药型罩形成EFP过程,是不会出现较大的材料断裂的,与Steinberg本构方程描述药型罩材料所得到的图3、图4物理云图矛盾,故选取Steinberg本构方程描述药型罩(EFP)成型并不合适。
2.1.2 药型罩材料选取Johnson-Cook本构方程
表4为EFP成型过程中的头尾速度,与表3规律基本一致,但是存在差异,集中表现在:随着时间的延长,采用J-C本构,所得到的弹丸头部速度下降更多,尾部速度上升也更快,在当t=0.212 ms时,弹丸头尾速度均为2 240 m/s,弹丸首尾速度差为0,可认为此后弹丸保持稳定,而此时弹丸头部飞行距离已经达到炸高。表明从药型罩开始变形到形成稳定飞行的EFP开始侵彻靶板,仅飞行了500 mm,与在试验所得最佳炸高相符合。
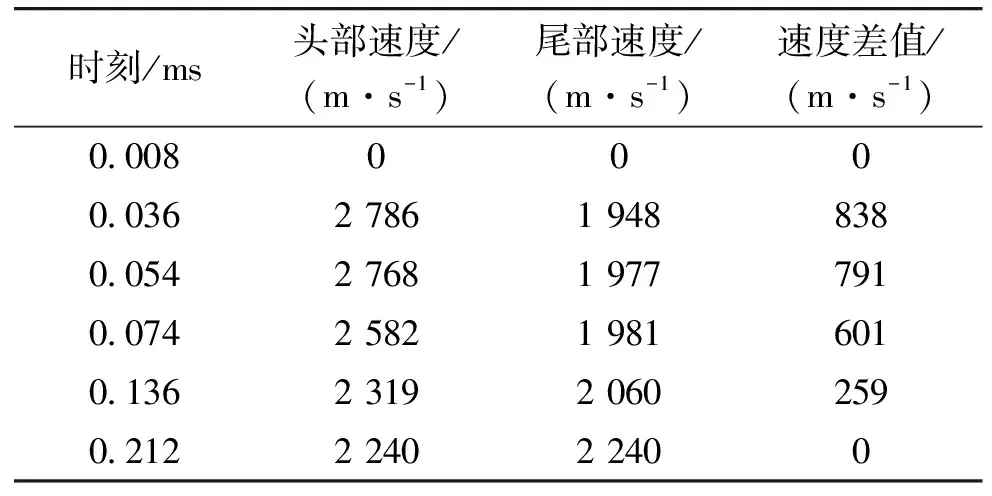
表4 J-C本构对应EFP成型过程头尾速度值
图5为EFP成型过程3个典型时刻的塑性应变分布,在0.074 ms、0.136 ms和0.212 ms时尾部材料塑性应变分别为0.9、1.1和0.8,显著低于图3中Steinberg本构模型描述的EFP成型过程中的塑性应变,故塑性变形产生的热也将低于前者,且弹丸尾部材料未与主体分离。这主要由于在J-C本构方程中,材料显示强度与其应变率正相关,比较图5(c)和图5(b),在0.136~0.212 ms时间段内,可以看到尾部材料仍然高速变形,材料显示强度就很高,对发生的变形破坏有较好的抵抗能力,射弹保持完整。
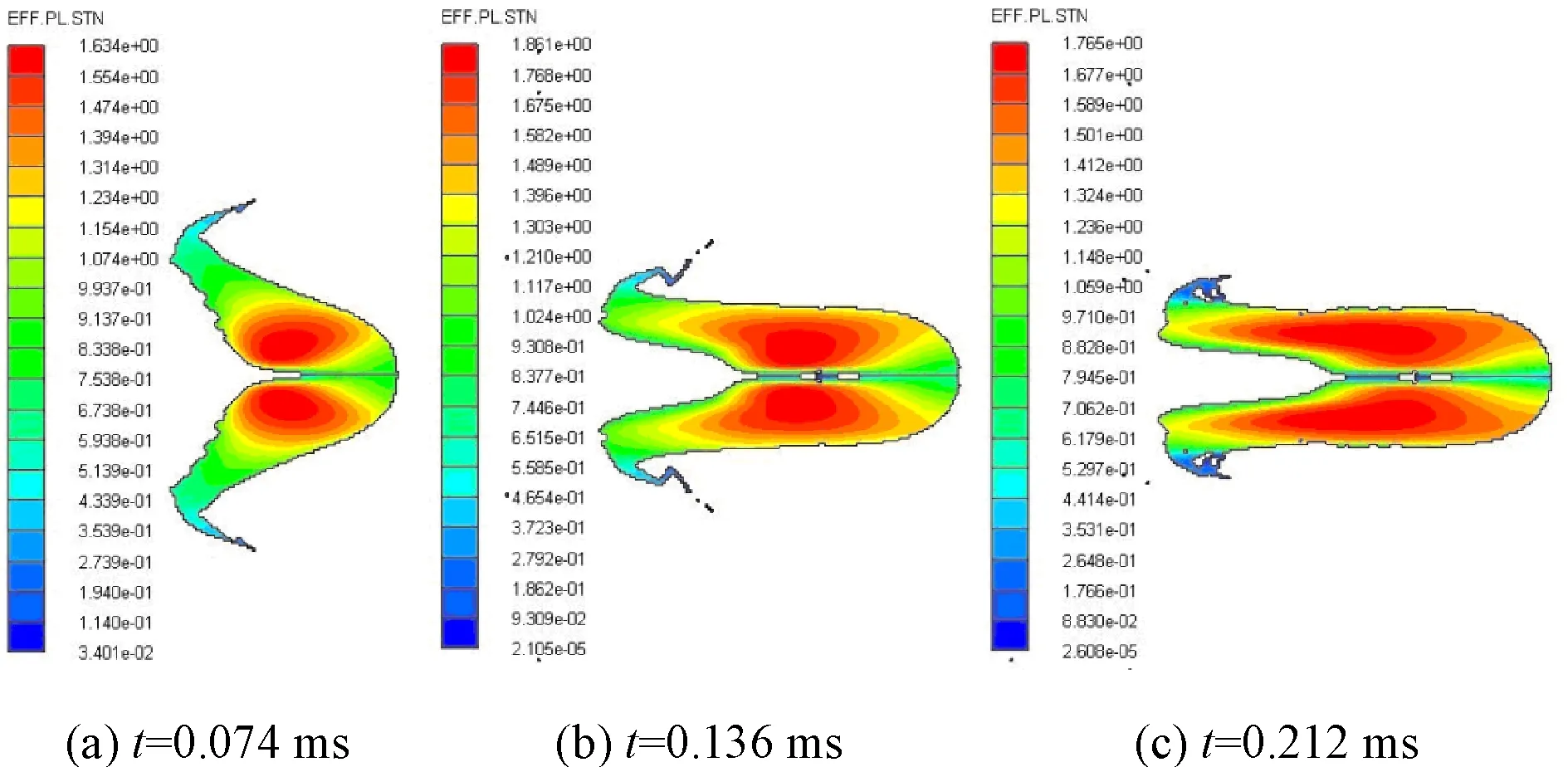
图5 J-C材料本构模型计算的EFP成型过程等效塑性应变场
2.2 侵彻过程
图6给出了2种本构模型对应的EFP在侵彻靶板的过程中轴向平均速度与加速度曲线的对比,它们并没有表现出像成型过程中很高的重合度。从减加速度曲线的对比中可以看出,J-C本构模型对应的EFP在侵彻过程中的峰值过载较高,约为5.0×107m/s2,而Steinberg本构模型对应的峰值过载为4.25×107m/s2,但是侵彻前期(0.217~0.260 ms)和后期(0.280~0.300 ms)Steinberg本构模型对应的过载高于J-C本构模型,侵彻中期相反。
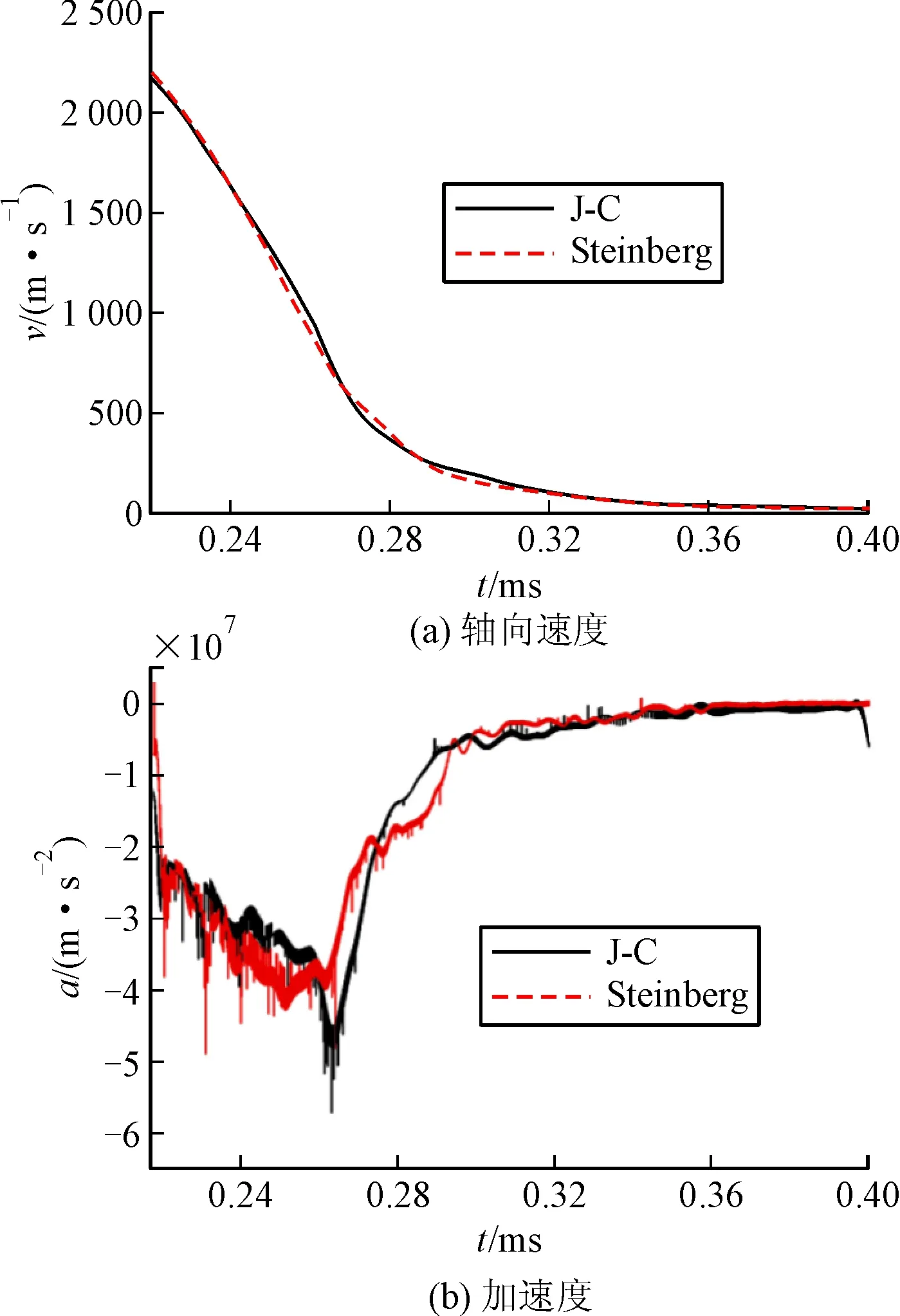
图6 2种本构模型侵彻过程中EFP轴向速度与加速度比较
实验测量侵彻深度为90 mm。J-C本构和Steinberg本构所模拟的侵深分别为85 mm和85.2 mm,开坑直径均为78 mm,与试验结果十分吻合,说明文中的数值模拟方法正确,分析合理。图7为EFP侵彻靶板的效果比较,可以看出2种本构模型所得到的最终侵彻图像相差不大,2种模型的主要差别在EFP成型过程。

图7 侵彻靶板效果图比较
3 结论
由以上对比分析可知,在文中给出的弹药结构模型下,对药型罩材料使用J-C本构和Steinberg本构均能很好的模拟EFP的成型和侵彻过程,在稳定飞行速度和侵彻结果上相差不大,并与试验相符。但有以下几点不同:
1)在EFP的成型中,Steinberg本构所模拟的EFP塑性应变都远大于J-C本构。
2)EFP成型时,Steinberg本构下EFP尾部有较大部分与主体分离;J-C本构下EFP有“尾翼”,完整性较好。
3)J-C本构对应的EFP在侵彻过程中的峰值过载高于Steinberg本构,侵彻前期和后期Steinberg本构对应的过载高于J-C本构模型,侵彻中期相反。
因此建议球缺药型罩EFP成型及侵彻模拟计算中对紫铜药型罩材料应优先选取J-C本构模型。
参考文献:
[1] 林加剑. EFP成型及其终点效应研究 [D]. 合肥: 中国科学技术大学, 2009: 14-16.
[2] 常向阳, 王自力. 爆炸成型弹丸侵彻钢靶的ALE算法 [J]. 解放军理工大学学报, 2004, 5(3): 70-73.
[3] 桂毓林, 于川, 刘仓理, 等. 带尾翼的翻转型爆炸成形弹丸的三维数值模拟 [J]. 爆炸与冲击, 2005, 25(4): 313-317.
[4] 蒋建伟, 杨军, 门建兵, 等. 结构参数对EFP成型影响的数值模拟 [J]. 北京理工大学学报, 2004, 24(11): 939-941.
[5] 杨秀敏. 爆炸冲击现象数值模拟 [M]. 合肥: 中国科学技术大学出版社, 2010: 6-10.
[6] JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures, and pressures [J]. Engineering Fracture Mechanics, 1985, 21(1): 31-48.
[7] STEINBERG D J. Equation of State and Strength Properties of Selected Materials [M]. [S.l.:s.n.], 1991.
[8] Century Dynamics Inc. Autodyn theory manual, revision 412 [M]. San Ramon: Century Dynamics Inc, 2001.
