带落角约束的鸭/尾舵复合控制导弹制导控制一体化设计
2017-05-03于云峰凡永华
潘 瑞, 于云峰, 凡永华
(西北工业大学航天学院, 西安 710072)
0 引言
鸭舵和尾舵是导弹气动舵的基本形式。鸭舵控制导弹效率高,动力响应快,但是鸭舵控制的导弹在初始发射段等情况下,需极速转弯,舵面较易饱和;而安装在尾部的尾舵,其大力矩臂使得只需要较小的舵偏即可实现对大攻角的控制,但尾舵控制导弹响应具有延迟。采用鸭/尾复合控制舵面,不仅可以综合单一舵控制的优点,并且可以通过对舵面的合理配置,实现低动压、大过载下的飞行,提高跟踪指令的快速性。
常规系统设计过程是将导弹控制回路设计和制导回路设计分开串联进行,但实际上制导环节和控制环节并不相互独立[1],因此独立的设计方法使得制导回路与控制回路的匹配性能难以达到最优。而制导控制一体化设计从设计之初就是将制导与控制综合考虑,因而能最大限度的挖掘导弹的过载潜力,提高制导精度。
在导弹制导控制一体化设计方面,已有学者进行了研究。文献[2]针对打击固定目标的飞行器进行了制导控制一体化的设计;文献[3]选择零脱靶量作为滑模面,极大简化了制导控制一体化设计,但是并未解决颤振的问题。针对复合控制问题,文献[4]结合滑模方法,将鸭舵和尾舵两个执行机构的控制作用结合在一起。针对带落角约束问题,文献[5]宋建梅等设计了带落角约束的制导律,并且解决了起控点过载较大的问题。
针对导弹大落角攻击时单一舵面易出现饱和的问题,文中以鸭/尾舵复合控制导弹作为研究对象,进行了带落角约束的制导控制一体化设计。首先通过设计两个滑模面来使落角达到期望值,并且利用指数趋近律克服了滑模控制的抖振问题,最后对拦截目标的过程进行了仿真,仿真结果表明制导控制一体化方案的可行性。
1 制导控制一体化模型
纵向平面内弹目相对运动关系如图1所示。
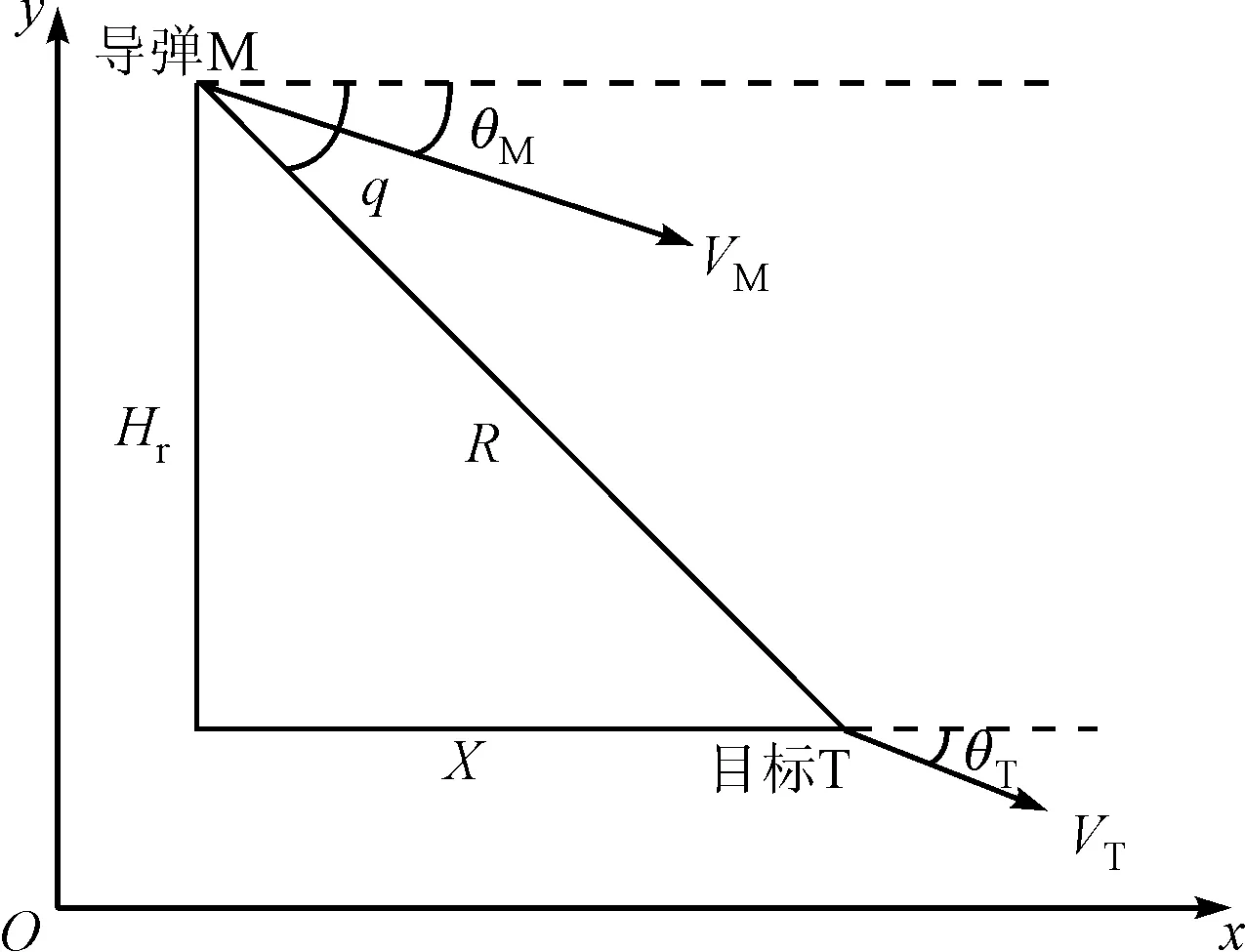
图1 弹目相对关系图
图1中:下标M、T分别表示导弹和目标;R为弹目相对距离;q是视线角;θ为弹道倾角。由几何关系得到如下导弹与目标的相对运动学方程:
(1)
从图中可以看出:
(2)
式中:Hr表示导弹与目标之间的高度差;R表示弹目之间的相对距离。在时间Δt内视线角增量为:
(3)
如果时间Δt较小时,Δq也为小量,因此可以进行近似:
(4)
对式(4)进行微分可`以得到:
(5)
对式(5)再进行微分可以得到:
(6)
式中:aMy、aTy分别代表导弹和目标的机动加速度在Oy上的分量,由:

(7)
及Δq是一个较小的量,故有:
(8)
在这里只研究纵向平面运动,不考虑导弹的侧向运动,并且假设α、δz、δc均较小[6]。可以得到导弹的俯仰通道模型为:
(9)
(10)
由于导弹相对于目标在速度机动能力上占有绝对优势,故可将目标机动视为干扰,即f=aT。
综上所述,导弹的制导控制一体化模型为:

(11)
式中:
2 滑模控制器设计
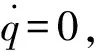
第一个滑模面选取为:
(12)
即:
(13)
对上式进行微分可以得到:
(14)
选择指数趋近律:
(15)
结合式(14)可得控制器为:
(16)
由于鸭舵控制对导弹的制导性能起主要作用[7],同时为了充分发挥鸭/尾舵的优势,改善导弹的响应,应在第一个滑模面的基础上另外再选取一个滑模面,使导弹的落角最终为所需求的落角,同时充分发挥鸭舵的特性[8],故取第二个滑模面为:
S2=(Mα-Mδc)α
(17)
则:
(18)
利用指数趋近律:
(19)
则可解出控制量:

(Mα-Mδc)(ωz-a34α-a35δz)]
(20)

(21)
则:
(22)
将控制率代入得:
(23)
由上式可得,当:
ε1+C2M>0
(24)

3 仿真验证
本节利用某型导弹的气动参数和上述的制导控制一体化系统的方法进行设计,并对纵向平面进行了仿真。仿真初始条件为:导弹初始速度为4Ma,初始高度为10 000 m,初始水平位置为0 m,俯仰角为0°,攻角为0°;目标速度为2.5Ma,初始高度为7 000 m,初始水平位置为6 408 m,进行平飞巡航;则初始弹目距离为7 000 m,视线角为-25°,期望的视线角为-60°,导弹的最大舵偏为30°。仿真结果如图2~图6所示。

图2 弹目距离变化曲线

图3 视线角变化曲线
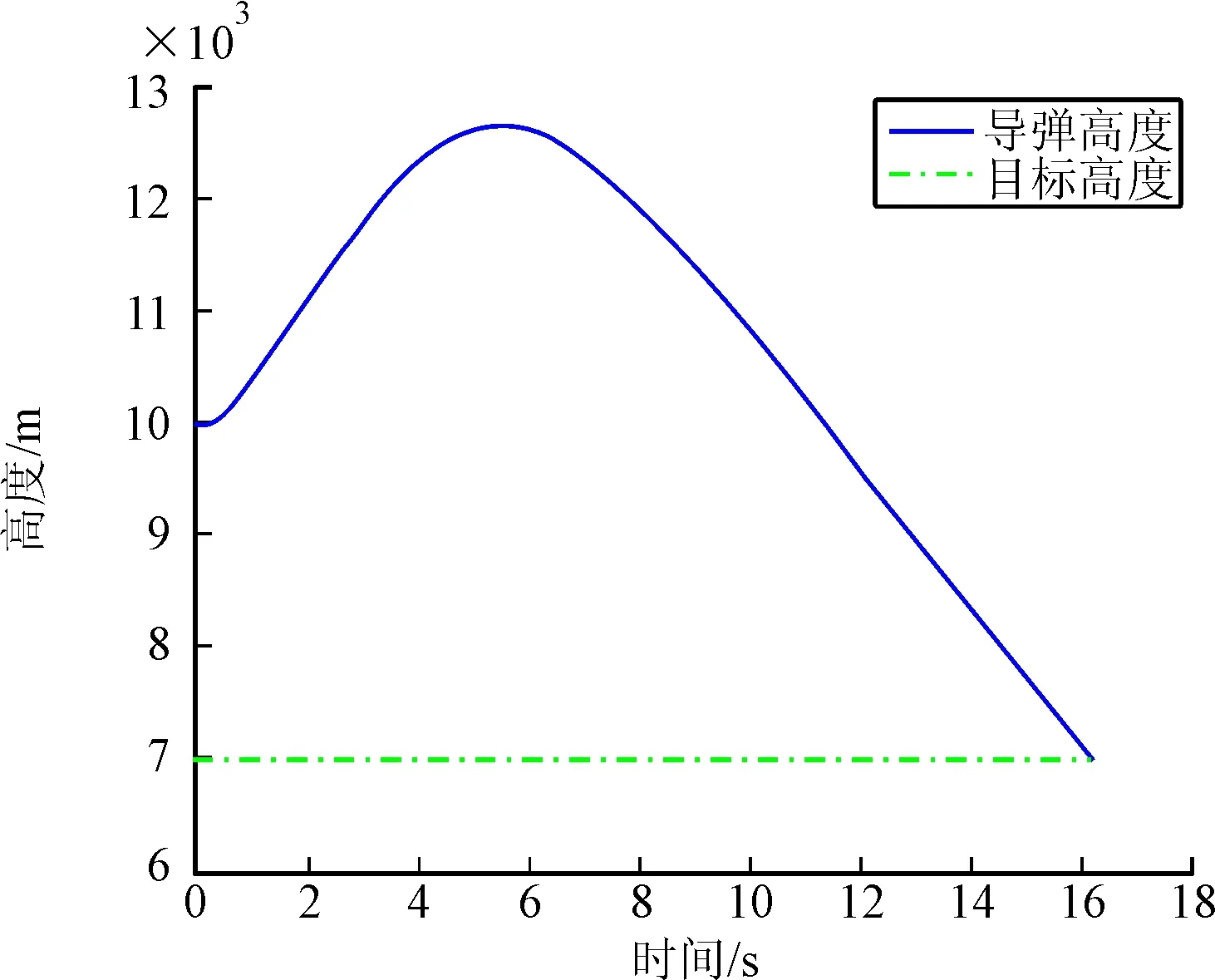
图4 导弹和目标视高度变化曲线

图5 导弹和目标水平位移变化曲线
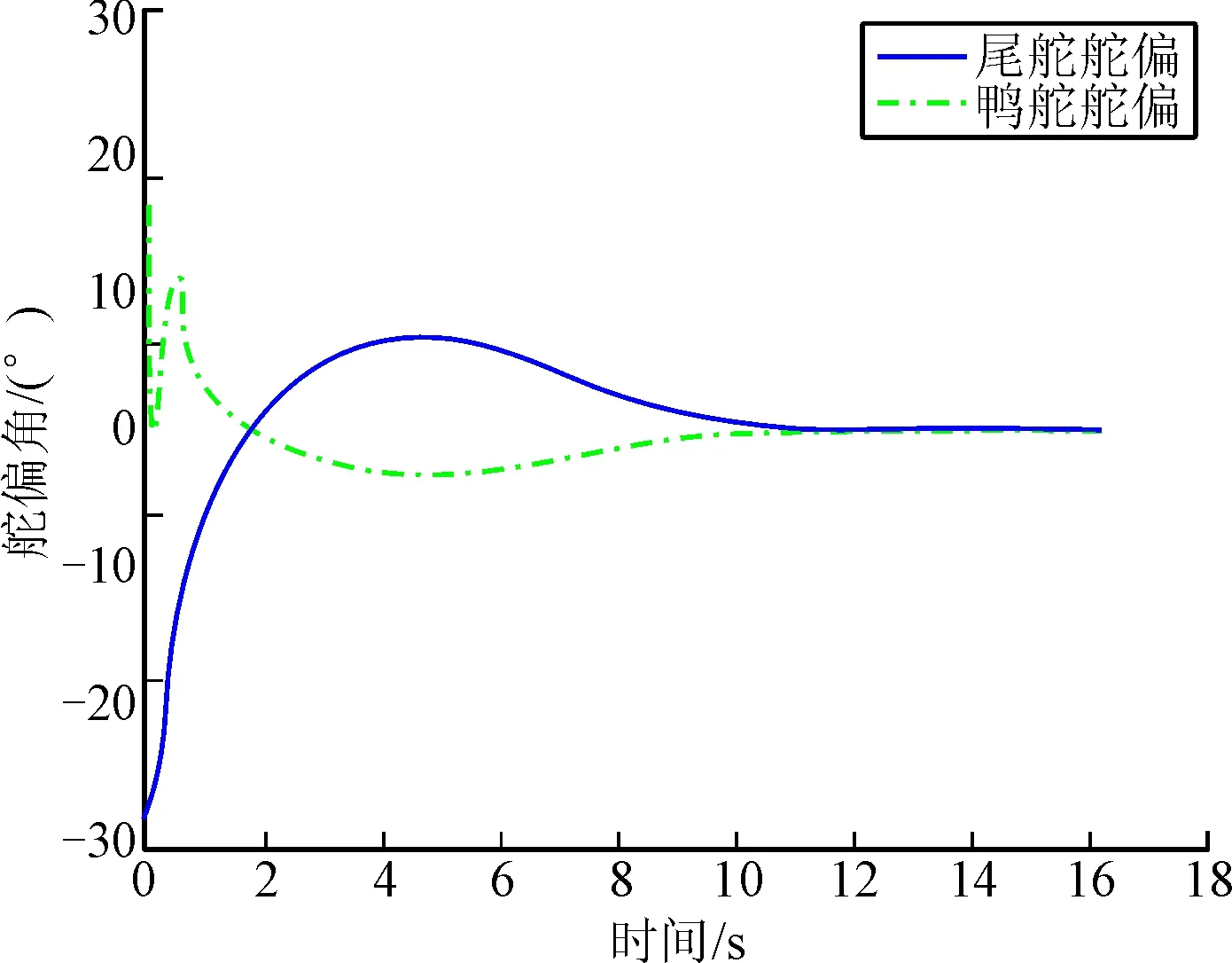
图6 舵偏变化曲线
由仿真结果可以看出:采用制导控制一体化设计方法能够击中目标,所用时间为16.238 s,脱靶量为0.57 m,落角能够平滑的收敛到期望值,最终落角为-59.96°,即采用文中设计的带落角约束的控制器能够满足落角要求,同时有效的避免了舵偏饱和现象的出现。
4 结束语
文中针对导弹大落角攻击时单一舵面易出现饱和的问题,以鸭/尾舵复合控制导弹为研究对象,采用了滑模方法设计了导弹的一体化制导控制系统。首先,建立了导弹纵向平面的一体化模型,并选取了带有落角约束的滑模面,从而推导出控制器的形式。最后通过仿真结果可以说明采用文中设计的一体化制导控制器能够满足落角要求,表明了该方法的有效性。
参考文献:
[1] 李运迁. 大气层内拦截弹制导控制及一体化研究 [D]. 哈尔滨: 哈尔滨工业大学, 2011.
[2] 查旭, 崔平远, 常伯浚. 攻击固定目标的飞行器制导控制一体化设计 [J]. 宇航学报, 2005, 26(1): 13-18.
[3] SHIMA T, IDAN M, GOLAN OM. Sliding-mode control for integrated missile autopilot guidance [J]. Journal of Guidance, Control, and Dynamics, 2006, 29(2): 250-260.
[4] BHAT M S, BAI D S, POWLY A A, et al. Variable structure controller design with application to missile tracking [J]. Journal of Guidance, Control, and Dynamics, 2001, 24(4): 859-862.
[5] 宋建梅, 张天桥. 带末端落角约束的变结构导引律 [J]. 弹道学报, 2001, 13(1): 16-20.
[6] 李新国, 方群. 有翼导弹飞行动力学 [M]. 西安: 西北工业大学出版社, 2005: 176-179.
[7] SHIMA T. Capture conditions in a pursuit-evasion game between players with biproper dynamics [J]. Journal of Optimization Theory and Applications, 2005, 126(3): 503-528.
[8] 赵国荣, 韩旭, 胡正高, 等. 基于模糊滑模方法的双舵控制导弹制导控制一体化 [J]. 控制与决策, 2016(2): 267-272.
