金属热黏塑性本构关系的研究进展*

王 强，王建军，张晓琼，张天辉，王怀坤，吴桂英

（太原理工大学机械与运载工程学院，山西 太原 030024）

材料的本构关系研究是理论与应用力学领域的重要课题。在工程应用中，选择合适的本构关系来描述材料的力学行为，是进行工程结构承载与失效分析的前提。在航空航天工程、军事工业等领域中，材料常处于高温、高应变率的极端环境，对处于这种极端环境下的结构进行数值分析，需要首先建立准确的材料热黏性本构关系。

金属的塑性流动是指金属在外力作用下产生非弹性变形或屈服后的应力与应变关系。金属材料的塑性流动与温度密切相关，温度升高，金属的流动应力减小，即热软化，如图1 所示。金属的塑性流动实际上主要是位错越过各种障碍的运动过程，通常，阻碍位错运动的障碍分为两种：短程障碍和长程障碍。短程障碍可通过热激活克服，而长程障碍对温度不敏感。因此，对应的金属流动应力通常可由热激活部分和非热部分组成。

图1 不同应变率下93W-Ni-Fe 的流动应力随温度的变化曲线[4]Fig. 1 Flow stress-temperature curves of 93W-Ni-Fe at different strain rates[4]

同时，流动应力的应变率效应也是材料中普遍存在的现象，不仅反映在力学性能和破坏模式的差异上，也体现在材料微观机制随应变率的变化差异上，例如，屈服强度的变化和加工硬化的差异。许多学者针对多种已在工程领域中被广泛应用的金属材料进行了研究，探索了应变率对其流动应力的影响机制，如2024-T351 铝、6 061-T6 铝合金、OFHC 铜、4340 钢、Ti-6Al-4V 合金。为了研究材料在不同变形率下的服役性能，揭示材料的变形机制，需要针对金属材料的应变率效应开展系统研究，可为设计性能更优异的新材料提供试验和理论基础。

随着金属材料的广泛应用，需要建立材料的热黏塑性本构关系为其工程应用提供理论依据。描述金属塑性流动行为的本构关系的发展已有很长的历史，现有的本构关系通常被分为经验型/唯象本构关系和物理概念本构关系。唯象本构关系主要包括Johnson-Cook 本构关系（J-C 模型）、K-H 本构关系（K-H 模型）等，物理概念本构关系主要包括Zerilli-Armstrong 本构关系（Z-A 模型）、力学阈值应力本构关系（MTS 模型）、Bonder-Partom 本构关系（B-P 模型）等。材料热黏塑性本构关系不仅是理论与应用力学领域的重要研究课题，且随着计算机技术的兴起，也成为了计算力学的重要组成部分。

为了系统地介绍可以描述在不同温度、不同应变率下金属塑性流动行为的热黏塑性本构关系，本文中首先介绍几种常见的金属热黏塑性本构关系，详细讨论其优势、不足以及其修正形式，然后系统介绍考虑了第三型应变时效的金属热黏塑性本构关系、考虑K-W 锁位错结构引起的反常应力峰的金属热黏塑性本构关系以及考虑拉压不对称性的金属热黏塑性本构关系的研究进展。

1 常见金属热黏塑性本构关系及其修正形式

金属热黏塑性本构关系的发展已有数十年的历史，已建立了数种常见的金属热黏塑性本构关系。在工程应用中，如何选用合适的热黏塑性本构关系成为关注的重点。为此，本节将对几种常见的金属热黏塑性本构关系及其优缺点进行分析，并介绍其修正形式。现有的金属热黏塑性本构关系分为唯象本构关系（或经验型本构关系）和物理概念本构关系，唯象本构关系通常具有更简洁的形式，因此在工程中应用广泛，而物理概念本构关系是基于金属材料的塑性变形机理建立起来的，适用范围更广。

1.1 唯象本构关系

1.1.1 Johnson-Cook 本构关系

J-C 本构关系是Johnson 等于1983 年建立的一种唯象本构关系。J-C 本构关系由于形式简单、参数容易获得而被广泛应用，并被嵌入ABAQUS、ANSYS 等商用有限元软件中。J-C 本构关系认为金属的等效流动应力可表示为等效应变函数、等效应变率函数和温度函数的乘积，具体形式为：

式中： σ 为等效流动应力； ε 为等效塑性应变； ε ˙= ε˙/ε˙为无量纲塑性应变率，其中 ε˙ 为塑性应变率， ε˙为参考应变率；=(-)/(-) 为无量纲温度，其中为绝对温度，为熔化温度，为室温；、、、和为材料常数，其中，为参考温度和参考应变率下的屈服应力，为应变硬化系数，为应变硬化指数，和分别代表应变率硬化系数和热软化系数的材料常数。

J-C 本构关系形式简单，其材料常数通过少量试验即可获得，但其对一些金属的塑性流动行为的预测结果并不理想，难以实现本构关系形式简单和预测精度高之间的平衡。通常认为J-C 本构关系的缺点包括以下两个方面：

（1）对于一些金属材料，其流动应力随对数应变率呈非线性关系，这使得J-C 本构关系不能准确描述这些金属材料塑性流动行为的应变率敏感性，同样，对于一些金属材料，J-C 本构关系不能准确描述其塑性流动行为的温度敏感性，如图2 所示；

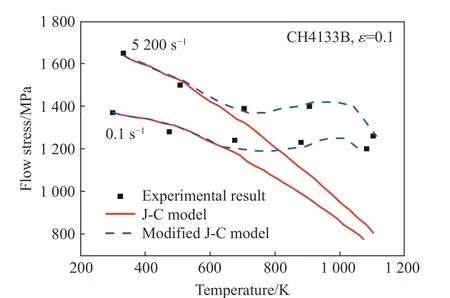
图2 不同应变率下，流动应力随温度变化的模型预测结果与试验结果比较[23]Fig. 2 Comparison of model predictions and experimental results of flow stress variation with temperature at different strain rates[23]

（2）对于金属塑性流动行为中的等效应变、等效应变率和温度对流动应力的影响为非独立的现象，J-C 本构关系同样不再适用。

针对J-C 本构关系的缺点，学者们建立了多种修正的J-C 本构关系。对于J-C 本构关系的第一类缺点，Holmquist 等通过对OFHC 铜的泰勒冲击试验发现，应变率对材料强度的影响不是J-C 本构关系所描述的为对数应变率的线性函数，而是应变率指数函数。为了更好地描述这种行为，将J-C 本构关系中的应变率项修正为无量纲塑性应变率的幂函数：

式中：和为经验系数。

对于J-C 本构关系的第二类缺点，Vural 等通过试验发现，实际的应变硬化项下降的速度比J-C 本构关系的预测值更快，这是由J-C 本构关系中的温度软化项决定的。为了描述这一现象，其在耦合温度和应变硬化项的同时，在应变率敏感项部分加入了温度效应，以便能更好地反映温度对应变率敏感性的影响。其形式为：

和分别为准静态应变率范围内（ ε ˙＜ε˙）的率敏感度和动态应变率范围内的率敏感度（ε˙＞ε˙）， ε˙为将准静态变形与动态变形分离开的过渡应变率，为室温，为参考温度，为Heaviside阶跃函数的近似，为比例因子，、为材料常数。图3 所示为2139-T8 铝合金单轴拉伸的试验结果与修正的J-C 本构关系预测结果的比较。

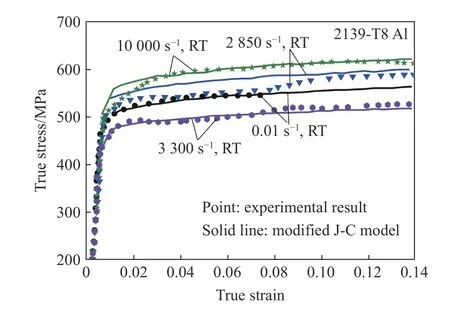
图3 试验应力-应变曲线与修正的J-C 本构关系预测结果的比较[27]Fig. 3 Comparison betwwen experimental stress-strain curves with MJC model predictions[27]

Lin 等通过对2124-T851 铝合金和高强合金钢在宽温度、宽应变率范围内的拉伸塑性流动行为进行分析，提出了一个考虑温度和应变率耦合效应的J-C 本构关系：

式中：、、 λ和 λ为材料常数。

此外，还有许多学者针对金属材料的热黏塑性流动行为建立了修正的J-C 本构关系，极大地拓宽了J-C 本构的使用范围。例如，Dou 等不仅考虑了应变、应变率和温度效应，而且考虑了应力状态效应，提出了一个塑性模型，确定了Ti-6Al-4V 合金在宽温度范围(93～1 073 K)和宽应变率范围（10～6.5×10s）下，不同应力状态(单轴拉伸、压缩和简单剪切)下的塑性行为和微观机制。

1.1.2 Khan-Huang（K-H）本构关系和Khan-Huang-Liang（K-H-L）本构关系

Khan 等对钽、含2.5%钨的钽合金以及AerMet 100 钢3 种BCC 金属进行了不同温度和不同应变率下的试验，发现J-C 本构关系和Z-A 本构关系无法准确描述这3 种材料的加工硬化随应变率变化的塑性流动行为。因此，为了更好地预测这3 种BCC 材料的加工硬化行为，他们耦合了应变和应变率对加工硬化的影响，建立了修正的K-H 本构关系：

针对Ti-6Al-4V 合金的塑性流动行为，Khan 等建立了一个修正的K-H-L 本构关系，并与J-C 本构关系的预测结果以及试验结果进行了对比，结果表明，修正后的K-H-L 本构关系比J-C 本构关系对Ti-6Al-4V 合金塑性流动行为有更好的预测结果，如图4 所示。修正后的K-H-L 本构关系为：

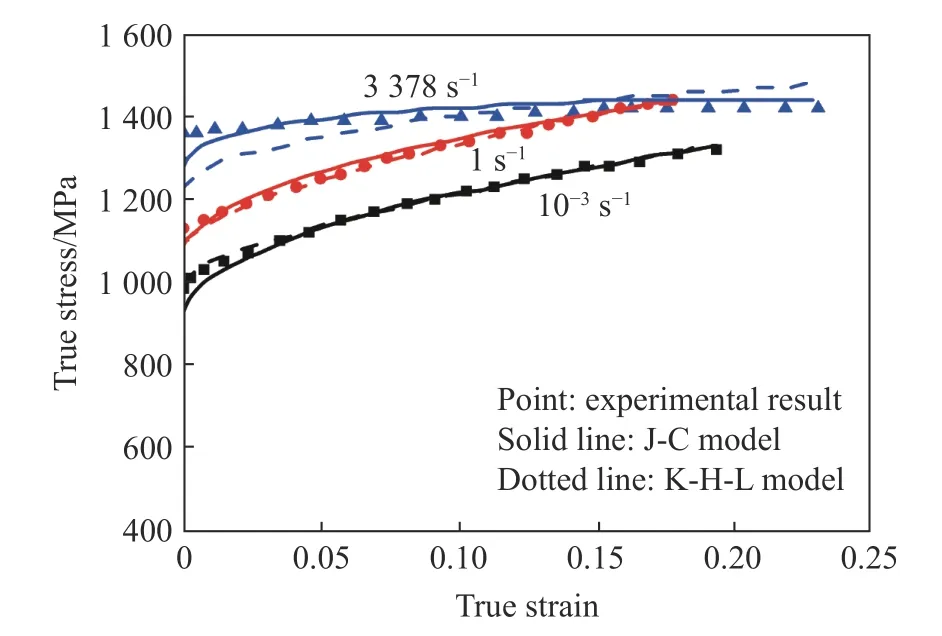
图4 不同应变率下，Ti-6Al-4V(296 K)的准静态和动态加载试验结果与K-H-L 和J-C 本构关系预测结果的比较[13]Fig. 4 Quasi-static and dynamic loading experimental results of Ti-6Al-4V (at a temperature of 296 K) for different strain rates with correlations using K-H-L and J-C models[13]

为了描述晶粒细化引起的不同多晶金属的塑性流动行为，Farrokh 等基于K-H-L 本构关系，建立了与晶粒尺寸和温度相关的金属热黏塑性本构关系：

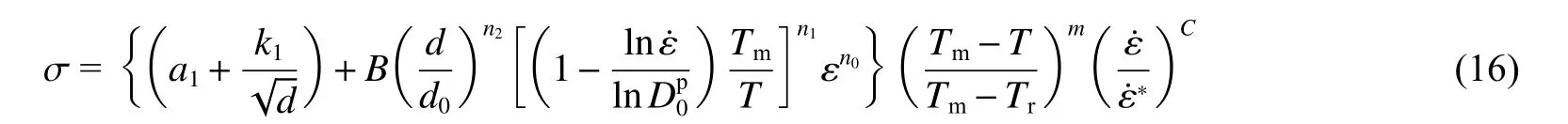
式中：为被测材料粗晶状态的平均晶粒度，为材料常数。图5 中给出了K-H-L 本构关系对不同晶粒尺寸纳米晶铝在不同应变率下的流动应力预测结果。

图5 不同晶粒尺寸纳米晶铝在不同应变率下的流动应力-应变试验结果与K-H-L 本构关系预测结果[38]Fig. 5 Observed and calculated responses for nanocrystalline aluminium at different strain rates by using KHL model for various grain sizes[38]

1.1.3 其他唯象模型

FCC 金属的真实应力-应变曲线可以通过指数形式表示，Voce和Kocks建立了V-K 本构关系。该指数律最初由Voce于1948 年提出，之后被许多研究者进行了扩展，其表达式为：

式中： δ为一个无量纲特征长度尺度细化率参数， δ为较大应变下特征长度尺度的饱和尺寸， δ和 δ分别为 δ和 δ的参考值，、和以及、和为描述微观结构细化和稳态特征长度对应变率和温度依赖性的常数。、和 ε˙、 ε˙为参考温度和参考应变率。图6 中给出了利用M-R 本构关系预测铜在冲击载荷下的塑性流动行为。Naderi 等将V-K 本构关系和M-R 本构关系结合起来描述了22MnB5 硼钢在等温变形下的应变、应变率和温度的依赖性。然而，该研究的不足在于只考虑了相对较低的应变率情况（小于10 s）。

图6 不同温度和应变率下铜的真实应力-真实应变曲线与预测结果的对比[41]Fig. 6 Comparison of true stress - true strain curves and model predictions for copper at different temperatures and strain rates[41]

为了能直观地了解各唯象本构关系的主要特性及其表达式，表1 中给出了各种唯象型本构关系的主要特征，表2 中给出了各种唯象型本构关系的方程形式。

表1 唯象型本构关系的模型对比Table 1 Comparison of phenomenological constitutive relations

表2 唯象型本构关系的方程形式Table 2 Equations of phenomenological constitutive relationships relations

1.2 物理概念本构关系

1.2.1 Bodner-Partom（B-P）本构关系

Bodner 等于1975 年建立了考虑应变硬化和黏性影响的大变形弹-黏-塑性本构关系。尽管该本构关系对应变率不是很敏感，且没有考虑温度效应，但B-P 本构关系的优势在于其坚实的物理基础。该本构关系将材料的总变形率分为弹性和塑性两部分，即：

式中：为最大应变率，为一个内部变量，表示材料的变形历史。应变率敏感度由参数控制。假定为塑性功的函数：

式中：、和为本构常数。

Huang 等使用B-P 本构关系描述了1100-0 铝在应变率为10～10s范围内的塑性流动行为。结果表明，B-P 本构关系可以准确描述1100-0 铝的应变率敏感性和在大塑性变形下的加工硬化。

由于B-P 本构关系没有考虑温度效应，所以Chen 等在B-P 本构关系中引入了热软化效应来描述30CrMnSiA 钢的塑性流动行为，其形式为：

式中：、和为本构常数。

图7 所示为B-P 本构关系预测得到的30CrMnSiA 在温度升高时流动应力的软化。马鑫等用B-P本构关系描述了Sn-Pb 共晶合金在10～10s应变率范围内、-55～125 ℃温度下的拉伸行为，其结果如图8 所示。

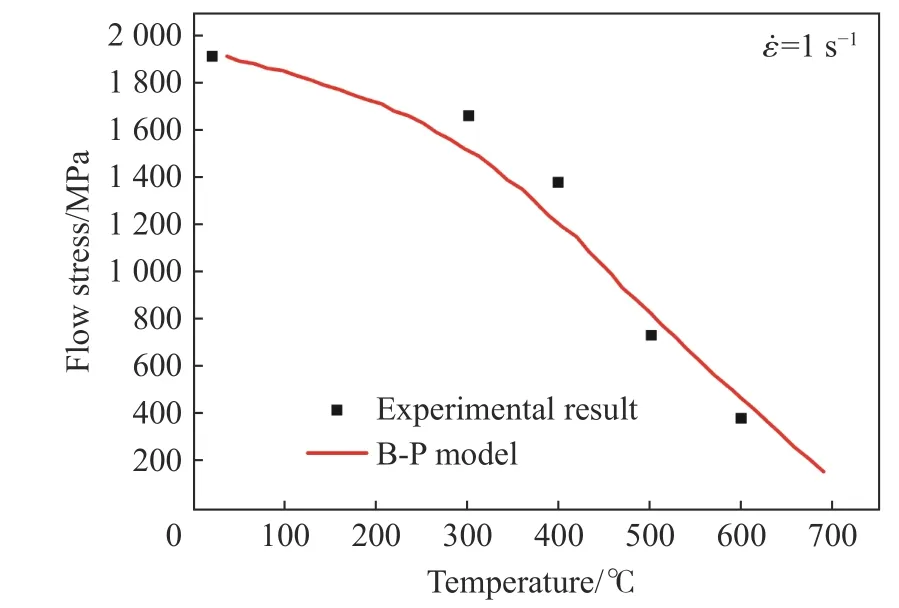
图7 30CrMnSiA 热软化情况的理论和试验值的比较[44]Fig. 7 Comparison between theoretical and experimental values on thermal softening of 30CrMnSiA[44]

图8 Sn60Pb40 合金的计算结果与试验结果的比较[45]Fig. 8 Comparison of calculated results and experimental results for Sn60Pb40 alloy[45]

1.2.2 Zerilli-Armstrong（Z-A）本构关系

Zerilli于1987 年基于位错力学建立了Z-A 本构关系，该本构关系考虑了应变硬化、应变率硬化和晶粒尺寸对金属材料流动应力的影响。由于温度和应变率对面心立方体金属材料（face-centered cubic，FCC）和体心立方体金属材料（body-centered cubic，BCC）的影响不同，例如BCC 金属比FCC 金属表现出更高的温度敏感性和应变率敏感性，所以FCC 和BCC 两类金属材料的Z-A 型本构关系形式也不同。对于FCC 金属，位错必须克服林位错的阻碍；对于BCC 金属，位错必须克服Peierls-Nabarro 障碍。因此，对于FCC 金属，Z-A 本构关系的形式为：

对于BCC 金属，Z-A 本构关系的形式为：

式中： σ为流动应力的非热分量，主要由溶质和晶界等因素确定， σ=σ+，其中 σ为考虑溶质和初始位错密度影响的屈服应力部分，为晶粒尺寸系数，表征微结构应力强度； α =α-αln ε˙ ，β=β-βln ε˙ ，、、α、α、β、β和σ为由试验确定的材料参数。

鉴于HCP（hexagonal close-packed，HCP）材料表现出与FCC 和BCC 金属类似的应变率敏感性和温度依赖性，例如钛金属，Zerilli 等将Z-A 本构关系的FCC 形式和BCC 形式统一，建立了一个新的本构关系，描述了Ti-6Al-4V 合金和HY-100 合金的塑性流动行为，其表达式为：

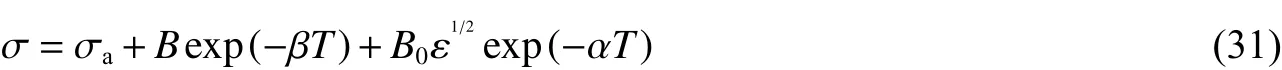
Z-A 本构关系中的参数在各种条件和整个变形过程中被视为常数，但是这种情况与实际情况是不符合的。因此Zhang 等建立了一个修正的Z-A 本构关系，描述了新开发的镍基高温合金IC10 在宽温域(293～1 073 K)和宽应变率(10～10s)下的塑性响应，该本构关系考虑了温度、应变率和变形过程对参数的影响。修正后的本构关系表达式为：

对于FCC：

除此之外，许多学者对Z-A 本构关系进行了修正以适应某些特定的材料。例如，Samantaray 等在Z-A 本构关系的基础上，考虑了温度与应变、温度与应变率的耦合效应对流动应力的影响，建立了一个新的本构关系，描述了Ti 改性奥氏体不锈钢(D9 合金)在1 073～1 473 K 温度范围、10～1 s应变率范围内的塑性流动行为，其本构形式为：

式中：、、、、和为材料常数。

Abed 等通过试验发现，Z-A 本构关系在预测热激活应力时，假定应力-温度呈指数关系。但是这种指数形式并不适用于所有类型的金属，特别是在高温下，这会导致Z-A 本构关系的热激活应力在任何温度下都不会消失，该假设与热激活理论相悖。因此，Abed 等建立了Z-A 本构关系的修正形式。

对于FCC：

对于BCC：

式中：=ln(1/ε˙) ；、和为与微观结构相关的材料参数；为一个附加的应力，与溶质、原始位错密度以及晶粒尺寸相关。

1.2.3 力学阈值应力（mechanical threshold stress，MTS）本构关系

在Z-A 本构关系中，流动应力的应变率相关性被分成两个区：滑移区和拖曳区，将FCC 金属的流动应力在应变率超过10s时的快速增长解释为变形机制的转变：从滑移区向拖曳区转变。然而Follansbee 等通过试验观察，认为应变率敏感性的上升应归因于结构演化的速率敏感性，因此，为了描述材料的高应变率行为，发展了MTS 本构关系，其形式为：

MTS 本构关系中考虑了应变、应变率和温度对流动应力的影响，所以需要大量的试验才能确定所需的材料参数，因此使用起来比较麻烦。Follansbee于1988 年总结回顾了MTS 本构关系的研究进展，加入了变形孪晶和多重强化机制，给出了MTS 本构关系的更一般的形式：

式中：S为与温度和应变率相关的因子，σˆ为热应力，一般取=2。

由于MTS 本构关系可以很好地预测高应变率范围（10～10s）内的流动行为，因此被研究人员用来模拟各种金属在宽应变率范围内的塑性变形行为。

Banerjee 等对不同退火的4340 钢进行了泰勒冲击试验，并使用MTS 本构关系预测了其在高温高应变率下的塑性流动行为。此外，学者们也将MTS 本构关系嵌入有限元程序，用来模拟金属材料在高应变率下的变形行为，如Maudlin 等采用Taylor 冲击试验、扭转试验、平板撞击和斜撞击试验的数据，在EPIC-2 和PINON 程序上对MTS 进行了评估，发现在剪应变小于0.2 的情况下，MTS 模型有很好的精度。

1.2.4 Nemat-Nasser-Li（N-N-L）本构关系

为了描述钽和钽钨合金在宽温度域、宽应变率范围、大变形条件下的塑性流动行为，Nemat-Nasser 等建立了一种金属热黏塑性本构关系，其表达式为：

图9 不同应变率和温度下，退火OFHC 铜的N-N-L 本构关系预测结果与试验结果的比较[57]Fig. 9 Comparison of model prediction predictions with experimental results for annealed OFHC copper at different strain rates and temperatures using N-N-L constitutive model[57]

Guo 等利用N-N-L 本构关系描述了3003 Al-Mn 合金的塑性流动行为，结果如图10 所示。此外，N-N-L 本构关系也被用于钼和钛等金属塑性流动行为的预测。

图10 不同应变率下N-N-L 模型预测与试验结果的比较[58]Fig. 10 Comparison between N-N-L model predictions with experimental results at different strain rate[58]

1.2.5 其他物理概念本构模型

除上述几种常见的物理概念本构关系外，学者们建立了其他的物理概念本构关系以描述金属材料的温度依赖性和应变率敏感性。例如，Rusinek 等基于Klepaczko的研究建立了一种热黏塑性本构关系（R-K 本构关系），用于描述金属铝薄板在10～10s应变率下的应变、应变率和温度与流动应力之间的关系。该本构关系中添加了一个有效应力，对应于应变硬化和热激活过程。其表达式为：

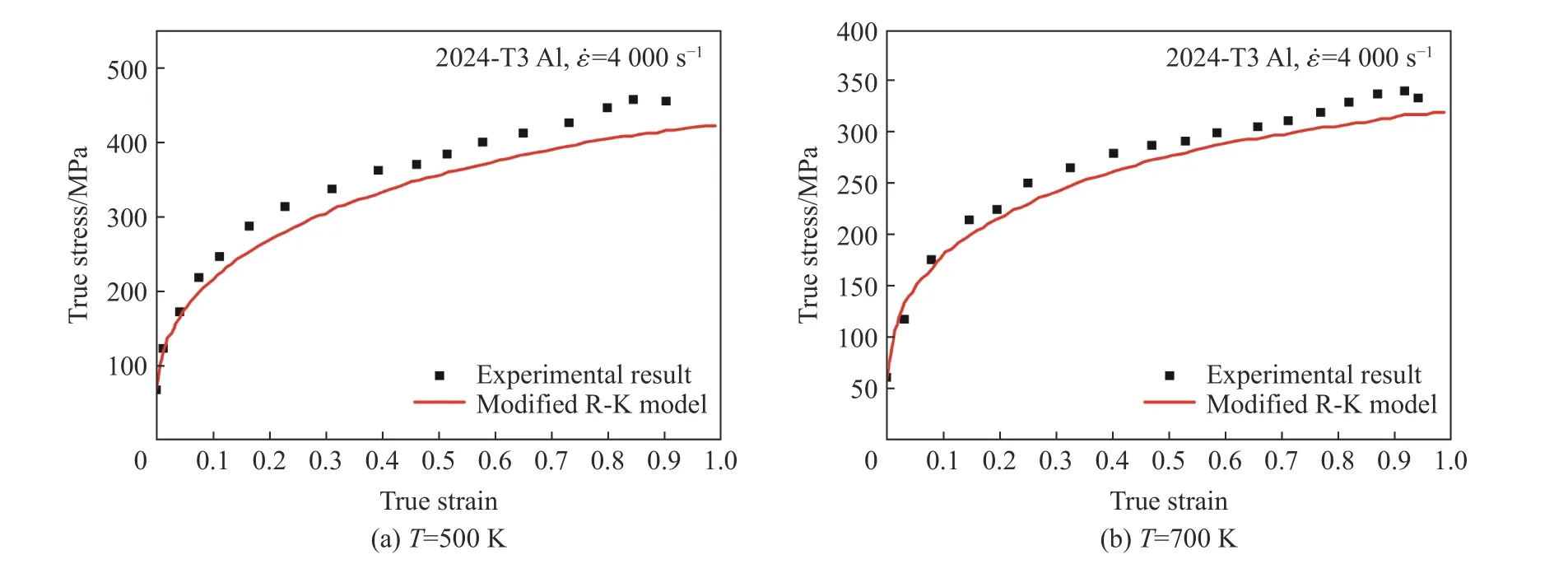
图11 用M-R-K 本构关系描述的流动应力随塑性应变的变化[65]Fig. 11 Change of the flow stress with plastic strain described using the M-R-K model[65]

Gao 等基于位错运动的热激活机制，建立了一种可以描述FCC 金属动态塑性行为的热黏塑性本构关系，该本构关系中本构参数与材料的微观结构特征直接相关，其形式为：

表3 物理概念本构关系的模型对比Table 3 Comparison of physically based constitutive relations

表4 物理概念本构关系的方程形式Table 4 Equations of physically based constitutive relations

此外，Xu 等近年来也对常见的各种金属热黏塑性本构关系的描述和预测能力进行了详细的研究和对比。主要针对B-P、N-N-L、Z-A、V-A 和R-K 等5 种物理概念本构关系以及J-C 和K-H-L 等2 种唯象本构关系，介绍了各本构关系参数的确定方法，分别用于描述典型FCC 金属铜和钨基复合材料93W-4.9Ni-2.1Fe在宽应变率宽温度范围内的塑性行为，分析了各本构关系在描述加工硬化、温度和应变速率影响时的灵活性。

2 包含第三型应变时效的金属热黏塑性本构关系

在宽温域、宽应变率范围内对金属材料的塑性流动行为进行测试时，会发现：在某应变率下，金属材料的流动应力-应变曲线随着试验温度升高整体或较大部分反而上升，表现在对应的流动应力-温度曲线上为出现一反常应力峰值，如图12 所示。考虑到这种现象在形式上有别于“静态应变时效”和锯齿屈服PLC 动态应变时效，郭伟国等，Wang 等和Xiao 等将这一现象称为“第三型应变时效”（third type SA，简称3rd SA）。第三型应变时效现象的出现具有普遍性，在单晶、多晶(BCC, HCP, FCC)等各类金属中都出现这一现象。

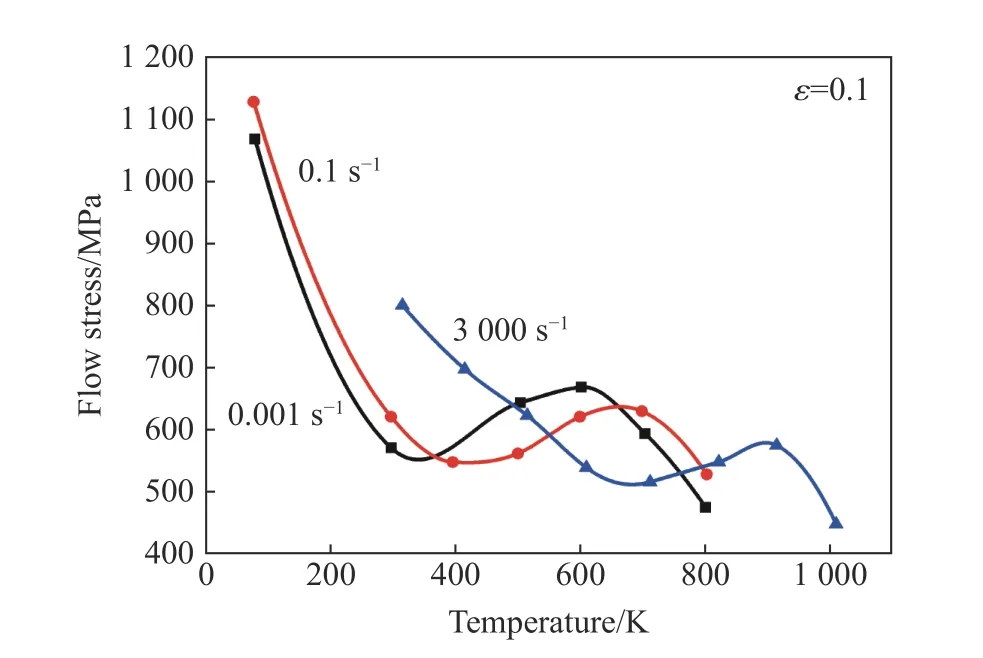
图12 DH36 钢流动应力随温度变化曲线上出现的反常应力峰[71]Fig. 12 Anomalous stress peaks in the flow stress curves of DH36 steel with temperature[71]

第三型应变时效现象的出现使得常见的金属热黏塑性本构关系不能很好地描述金属材料在第三型应变时效出现的温度区域内的塑性流动行为。为此，学者们通过对第三型应变时效的表现形式和微观机理的研究来建立考虑第三型应变时效的金属热黏塑性本构关系。Gilat 等在基于位错热激活理论建立的金属热黏塑性本构关系的基础上，增加了考虑局部溶质原子浓度的第三型应变时效项，利用建立的包含第三型应变时效的金属热黏塑性本构关系，可以很好地描述1020 钢在不同温度、不同应变率下的塑性流动行为。Cheng 等基于N-NL 本构关系考虑第三型应变时效过程中溶质原子浓度的变化，建立了包含第三型应变时效的金属热黏塑性本构关系，其最终形式如下：

其中并未考虑第三型应变时效现象的应变率效应。孟卫华等和Su 等同样在Nemat-Nasser 等建立的物理概念热黏塑性本构关系的基础上，增加了第三型应变时效项来描述DH-36 钢的拉伸和压缩塑性流动行为，考虑到第三型应变时效现象的应变率效应，通过对在很宽应变率范围内的试验结果进行进行分析，认为第三型应变时效项中的特征参数 σ、和与对数应变率呈线性关系，表达式为：

第三型应变时效现象的出现，使常见的金属热黏塑性本构关系不能很好地描述金属塑性流动行为，为此，学者们建立了多种包含第三型应变时效的金属热黏塑性本构关系，可分为两类：具有物理概念的本构关系和经验型的本构关系。具有物理概念的本构关系是基于第三型应变时效微观机理，即运动位错与溶质原子的相互作用建立起来的，其形式通常较复杂，材料参数不易获得。经验型的本构关系在常见金属热黏塑性本构关系的基础上增加了第三型应变时效项，由于其形式简单、参数容易获得，近年来受到了广泛关注。经验型的本构关系中的第三型应变时效项通常采用正态分布形式，但是其中的特征参数与应变率的关系式有一定差异。

3 包含K-W 锁位错结构引起的反常应力峰的金属热黏塑性本构关系

在对 γ相增强的镍基高温合金的塑性流动行为的研究中发现： γ相增强的镍基高温合金流动应力在随温度变化的曲线上，会出现一反常应力峰，如图13 所示。该反常应力峰的出现被认为是由镍基高温合金中 γ相中的K-W 锁位错结构引起的。学者们在观察和分析交滑移锁形成过程的基础上，成功发展出很多与K-W 锁的形成和解锁相关的超弯折模型。K-W 锁的形成过程为被压缩的超不全位错首先滑移到立方面上，然后扩展到一相交的八面体上，以非平面锁的形式锁住整个位错。超弯折模型的基础为O r o w a n 公式，包含S u n 模型、Hirsch 模型、ELU 模型和自解锁机制模型。

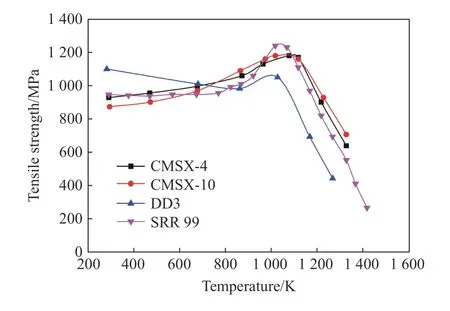
图13 镍基高温合金的拉伸强度随温度的变化[97-98]Fig. 13 Tensile strength of nickel base superalloy as a function of temperature[97-98]

为了描述γ′相增强的镍基高温合金DD407的力学行为，Wang 等建立了一个考虑屈服应力的异常温度依赖性及其应变率效应的本构关系。根据反常应力峰的特点，Wang 等修正了Johnson-Cook 本构关系以描述镍基高温合金GH4133B 的塑性流动行为。结合反相界面能的温度依赖性和经典的颗粒剪切理论，Li 等建立了一个温度依赖的屈服强度模型来描述 γ增强高温合金的屈服强度随温度的变化。

Wang 等基于镍基单晶高温合金的微观结构——一种含有 γ 基体相和 γ增强相的双相结构，建立了包含K-W 锁位错结构引起的反常应力峰的屈服强度与温度和应变率的关系。考虑 γ 相和γ相的影响，高温合金的流动应力可表示为：

式中：为玻尔兹曼常数，为位错运动的激活自由能，和为材料常数。

位错从八面体平面向立方体平面的交叉滑移，导致K-W 锁的形成，是屈服应力与温度正相关的根本原因。由于热激活滑移更倾向于立方体平面，导致材料在超过峰值应力对应的温度时发生软化。为了描述由K-W 锁引起的对位错运动的额外阻力的大小，可用正态分布来定量描述K-W 锁形成的概率随温度的变化， γ相的流动应力具体表达式如下：

式中：、 ζ 和为K-W 锁引起的反常应力峰值的特征参数，为K-W 锁产生的阻力最大时的温度，即峰值温度， ζ 为应力峰的宽度，为应力峰的高度。、 ζ 和为应变率的函数：

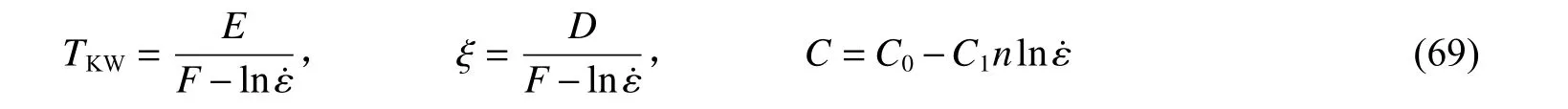
式中：、、、和为材料常数。

王建军等所建立的包含K-W 锁位错结构引起的反常应力峰的本构关系可以很好地描述γ相增强的镍基高温合金屈服应力随温度和应变率的变化，但未考虑塑性变形的影响。近期，Wang 等在对镍基高温合金K403 在宽温度域、宽应变率范围内的塑性流动行为进行测试时发现：高温合金K403 的流动应力随温度变化会出现两个反常应力峰，如图14 所示，通过系统分析，认为这两个反常应力峰分别由第三型应变时效和K-W 锁位错结构引起。为了能准确描述高温合金K403 的塑性流动行为，在文献[99]建立的 γ相增强的镍基高温合金的本构关系的基础上，在 γ 相的流动应力（ σ）中增加了第三型应变时效项，在固溶阻力部分（ σ）增加了非热部分。因此， γ相增强的镍基高温合金热黏塑性本构关系的最终表达式为：

图14 高温合金K403 在不同应变率下的流动应力随温度的变化Fig. 14 Flow stress of superalloy K403 as function oftemperature at different strain rates

如图14 所示，所建立的 γ相增强的镍基高温合金的热黏塑性本构关系可以准确地预测高温合金K403 在宽温度域、宽应变率范围内的塑性流动行为。

4 考虑拉压不对称性的金属热黏塑性本构关系

在钛合金和其他HCP 金属中经常观察到拉伸和压缩之间的强度差，即拉/压不对称。Khan 等研究了电子束单熔体Ti-6Al-4V 合金在不同应变率下的拉伸和压缩行为，发现Ti-6Al-4V 合金的拉伸和压缩行为不仅在屈服应力水平上有明显差异，而且在加工硬化速率上也有显著差异。Li 等研究了激光立体成形Ti-6Al-4V 合金(LSF Ti-6Al-4V)在宽温度域和宽应变率下的拉伸和压缩行为，发现拉伸和压缩力学行为在屈服应力和加工硬化速率上也存在显著差异。

在结构分析中，通常采用经典塑性理论来描述金属合金的塑性响应，该理论认为应力偏量的第一不变量和第三不变量对流动应力没有影响。然而，对于金属塑性流动行为中出现的拉/压不对称行为，塑性理论不再适用。岩土力学界早就认识到将静水压力(与应力偏量的第1 个不变量有关)和Lode 角参数(与应力偏量的第三个不变量有关)纳入本构关系的必要性。Richmond 等进行了初步研究，证明了静水压力对铝合金屈服的影响；Gao 等揭示了应力状态对5 083 铝合金的塑性响应有很强的影响，为应力状态相关的塑性模型的发展提供了蓝图；Khan 等提出了应变率和温度依赖的屈服准则来描述Ti-6Al-4V 合金的各向异性屈服行为和拉压不对称特性；Tuninetti 等研究了Ti-6Al-4V 合金的拉压不对称、各向异性屈服和各向异性应变硬化行为，基于宏观正交各向异性屈服准则CPB06，建立了考虑拉压不对称、各向异性屈服和各向异性应变硬化的弹塑性本构关系。

在Ti-6Al-4V 合金中经常观察到的流动应力拉/压不对称通常归因于滑移系统和机械孪晶的不同。LSF Ti-6Al-4V 合金的屈服应力和加工硬化速率具有显著的拉/压不对称，且其拉/压不对称与温度和应变速率有关。本文中将基于LSF Ti-6Al-4V 合金的塑性流动行为，建立一个考虑拉/压不对称以及温度和应变速率依赖性的金属热黏塑性本构关系。

式中： σ为初始缺陷引起的应力，为应变硬化系数，为应变硬化指数。 σ为由晶粒尺寸效应引起的应力。孪晶是LSF Ti-6Al-4V 合金的变形机制之一，孪晶细化晶粒提高了晶粒的抗滑移性和加工硬化率。由于孪晶对应变速率和温度的敏感性很低，因此将孪晶对流动应力的贡献纳入到非热应力中。Meyers 等提出，在大多数情况下，孪晶的粒度依赖性服从Hall-Petch 关系，且孪晶的斜率大于滑移的斜率。因此， σ可以表示为：

图15 为所建立的金属热黏塑性本构关系的预测结果与不同温度和应变率下LSF Ti-6Al-4V 拉伸和压缩应力-应变曲线的对比，可以看出，所建立的考虑拉/压不对称行为的金属热黏塑性本构关系可以很好地描述LSF Ti-6Al-4V 拉伸和压缩塑性流动行为。

图15 考虑拉压不对称行为的金属热黏塑性本构关系预测结果与试验结果的对比Fig. 15 Comparison between the predicted and experimental results of thermo-viscoplastic constitutive relationships of metal considering the asymmetrical behavior of tension and compression

5 总 结

热黏塑性本构关系能够描述最普遍情况下金属材料的变形行为，可预测金属材料在一定的温度和应变率范围内的塑性流动行为。传统唯象本构关系缺乏对物理机制的足够认识，所以无法准确描述材料塑性变形与微观结构演化的关系；而物理型本构关系考虑了材料在变形过程中的热变形机理。此外，由位错及其相互作用引起的加工硬化和温度升高引起的动态软化将导致热变形过程中特有的变形机制，所以能充分地描述这两种效应在金属热黏塑性本构关系中的作用，也是一个重要的研究领域。

由于第三型应变时效引起的反常应力峰、K-W 锁位错结构引起的反常应力峰以及拉压不对称行为的出现，使得常见的金属热黏塑性本构关系不再适用。为此，学者们针对3 种现象的微观机理、宏观特征等建立了考虑这3 种反常行为的金属热黏塑性本构关系，进一步完善了金属热黏塑性本构关系。