金属切削加工本构模型研究进展*

吕明航， 李安海,2， 吕豪剑， 葛德俊

(1. 山东大学 机械工程学院， 高效洁净机械制造教育部重点实验室， 济南 250061)(2. 山东大学， 机械工程国家级实验教学示范中心， 济南 250061)

在金属切削加工过程中，复杂的热力现象制约着加工技术的发展。随着计算机技术的发展，采用有限元方法来模拟加工过程，研究加工过程中复杂的热力耦合现象，成为一种重要的研究方向。而本构模型表征了材料应变、温度、应变速度等变形参数，决定了材料的力学行为[1]。因此，建立的有限元模型能否与真实加工精确吻合，本构模型是关键[2]。

为了准确地对加工过程进行仿真，国内外学者采用多种方法对本构模型进行了修正，主要分为唯象本构和物理本构2大类[3]。本文从几种常用的本构及其修正模型、模型中原始参数确认方法等方面进行总结及分析，为加工本构模型的建立和应用提供参考。

1 常用本构模型及其修正

1.1 Johnson-Cook模型及其修正

Johnson-Cook模型(JC模型)是由Johnson和Cook[4]在1983年提出的。该模型综合考虑金属材料加工过程中应变、应变率、温度等因素对流动应力的影响，建立了应变强化、应变率强化和温度软化的函数，可用于大变形、大应变率条件下的材料变形行为，模型的形式为：

(1)

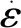
由于JC本构模型结构形式简单，且所需的材料参数较少，便于通过实验获取，在切削加工仿真中应用广泛。但是由于加工中会发生复杂变化，JC本构在某些情况下不能很好地反映加工的真实情况，因此各国学者对其做了大量的修正工作。

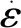
(2)

CHEN等[6]在对Ti-6Al-4V钛合金分离式霍普金斯压杆实验(SHPB)实验中发现应变硬化与温度相关，其随温度的变化会对流动应力产生影响。因此，他定义了一个温度函数Δ(T)来表征这种特性。柯志宏[2]在钛合金切削仿真中，在JC本构的基础上加入CHEN所定义的温度函数，形成新的模型：

(3)

KHAN等[7-8]在对钛合金的研究中发现塑性应变和应变速率之间存在着很强的相关性，二者相互作用对流动应力造成一定的影响。为了正确反映二者的相互影响，在JC模型基础上将应变强化项中的塑性应变与应变速率进行耦合，建立新的KHL模型：

(4)

CHENG等[9-10]在研究中发现加工过程中不同应力状态的变化也会对流动应力产生影响，因此在JC本构方程的基础上进行修正，加入应变状态项[1-cη(η-η0)]，形成新的本构方程：

(5)

ANDRADE等[11]在纯铜压缩实验中发现了在一定温度范围内流动应力随温度升高而降低的现象，认为这是由于材料内部再结晶软化的影响，从而提出在JC本构模型的基础上引入与再结晶温度有关的函数H(T)来修正这一现象。SEO等[12]将此本构模型应用于钛合金Ti-6Al-4V的加工仿真过程中，发现这种本构同样适用：

(6)

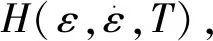
(7)

刘丽娟等[15-16]在对钛合金高速铣削切屑形态的微观研究中，发现由于加工过程高温和大变形的作用，使绝热剪切带发生动态再结晶现象，这使得材料软化程度增大，对材料的流动应力产生影响，促进了锯齿形切屑的形成和发展。在此基础上，建立了反映动态再结晶行为的本构方程：

(8)

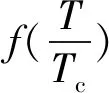
王琪等[17]在对钛合金高速切削研究中，同样发现温度达到临界温度时，材料会发生动态再结晶行为，使材料流动应力下降的现象。但他们对JC本构进行了不同的修正，采取引入一个连续温度函数式Y(T)的方法来反映钛合金在各个温度下的真实流动应力变化情况：

(9)

程国强等[18]在对HY-100钢的研究中，发现材料内部缺陷和夹杂在加工过程中会扩大聚集形成孔洞，到一定程度后产生破坏，会对材料的流动应力产生影响。通过在JC本构模型的应变项中增加反应材料损伤的软化项来修正：

(10)

滑勇之等[19]研究铝合金时，发现铝合金在到达一定温度时，材料会发生急剧软化，而JC本构中的热软化项无法满足材料的特性曲线，为了更好地描述这一特性，对热软化项Kt进行了修正：

(11)

CALAMAZ等[20]在对钛合金加工研究中，发现流动软化和应变软化等因素对流动应力的影响很大，因此在原本构模型的基础上引入分别反映应变软化和流动软化的修正项，形成新的Hyperbolic Tangent本构(TANH本构)：

(12)

这种本构模型被李川平等[21-23]采用。并且YAMEOGO等[23]认为新加入的软化项只有在重结晶发生时才会起作用，因此在仿真中同时使用JC本构和TANH本构，通过检测应变值是否达到临界值来确定哪种本构生效：

(13)

1.2 Zerilli-Armstrong本构模型及其优化

Zerilli-Armstrong模型(Z-A模型)是由Zerilli和Armstrong提出的[24]。Z-A模型是基于位错动力学形成的，能够很好地反应体心立方金属和面心立方金属的热变形行为，表达形式简单，获得了广泛的应用。

面心立方金属材料本构方程为：

(14)

体心立方金属材料本构方程为：

(15)

Zerilli和Armstrong在之后的研究中，对模型不断优化，建立了适用于密排六方金属的本构方程，并通过钛合金Ti-6Al-4V实验验证了其可行性。

(16)

但是Z-A模型也存在局限性，模型中的应变硬化率与温度和应变率之间的影响是相互独立的，但是大多数金属三者之间是相互耦合的，因此Z-A模型不适合于描述三者之间有强相关性的材料。

LIU等[25-26]在进行Ti-6Al-4V加工仿真时，发现传统的Z-A模型未能够反映剪切带形成过程中材料孔洞、微裂纹等对流动应力的影响。因此，其在原模型的基础上引入多重失效函数来表征这种现象：

(17)

1.3 GAO-ZHANG本构模型

除了常用的JC本构和Z-A本构模型外，国内外学者基于基础理论提出了新的本构模型。GAO等[27-28]在仿真密排六方金属加工时，以热激活位错理论为基础，建立了新的本构模型GAO-ZHANG模型(G-Z模型)。在此模型中，等效应力是由非热应力项和热应力项组成的：

(18)

1.4 多物理场模型

SHEN等[29-30]在对铜和铝合金切削仿真研究中，提出了一种基于位错密度的晶粒细化子模型，其原理如图1所示，通过模拟晶胞的拉长、细化等过程来体现加工过程的微观作用，修正流动应力。

(19)

同时，为了体现微观变化对流动应力的影响，ATMANI将临界应力模型和位错密度模型相结合，建立了一种多物理场模型，其耦合方式如图2所示。

2 本构模型参数的优化方法

本构方程的形式对仿真结果有影响，模型中的初始参数对于仿真结果也有很大的影响，因此众多学者对本构模型中原始参数的确定进行了大量的研究[33]。为了提高本构模型的修正精度，彭臣西等[34-35]采用单因素仿真实验方法探究JC本构模型5个系数(A、B、n、C、m)对切削力、切屑形态以及参与应力分布状态的影响。FENG等[36-37]通过热压缩试验测得铝、钛合金在特定温度范围的应力、应变值，确定了本构方程的原始参数。SEO等[12]采用分离式霍普金斯压杆实验(SHPB)研究了高温下钛合金的应变行为，并对本构方程中的原始参数进行了拟合。汪冰峰等[38]在根据SHPB实验数据拟合方程时，采用引入应力应变取向发展趋势项的方法，分两步拟合曲线，简化对温升等因素的估算。鲁世红等[3]利用SHPB实验所测到的数据，通过MATLAB应用自适应遗传算法来优化本构模型中的原始参数。

虽然SHPB实验被广泛应用于本构方程原始参数的确定过程中，但这种方法存在着一定的局限性：(1)SHPB实验所能达到的应变和应变率与真实切削加工还存在差距；(2)SHPB实验需要特殊的测试仪器且测试费用昂贵。因此，研究人员探索通过其他方式来获取原始参数。SHATLA等[39]开发了专用的计算机软件《OXCUT》来获取数据修正模型的原始参数。李川平[21]通过将正交切削实验数据与有限元仿真数据比较、迭代的方法，修正了钛合金在大应变、高应变率条件下的本构模型材料常数。叶玉刚等[40]在确定本构模型初始值时，在鲁世红等[3]所测参数的基础上，对多次有限元实验采用下山单纯型法迭代来确认原始参数。

杨勇等[41]提出有限元模拟和单因素流动应力公式计算联合建模的策略。先由单因素公式计算出与应变率对应的流动应力，再基于新的流动应力进行有限元迭代分析，通过反复迭代最终得到准确的本构方程。

上述本构方程在确定原始参数的过程中，每个参数是分别拟合的，而GAO等[27]认为单独拟合确定的参数不是整体上的最优解，因此提出采用全局算法和局部算法相结合的多目标非线性优化法来确定本构模型的最优原始参数，此方法确定的本构方程在仿真过程中得到更加精确的结果，其优化流程如图3所示。

3 结语

本构方程在金属加工仿真过程中有重要作用，目前对于本构方程的研究有了长足的发展和进步，但在以后的研究中还需要关注以下方面：

(1)对本构模型的建立只考虑了再结晶等变形机制的影响，对于加工过程中微观复杂的变化对流动应力影响的研究还不够深入，同时对宏微观作用的综合研究还不够完善。依据宏微观作用机制，建立多物理场耦合的本构模型是未来的研究方向。

(2)由于本构模型中原始参数的确定还不够准确，目前经过优化的本构模型仿真结果仍与实验结果存在差距。未来可以采取加工实验和计算机优化协同作用的方式来优化本构模型，使模型仿真结果更加精确。