导引头动力学建模方法研究

李富贵, 贾生伟, 赵 洪, 高 峰, 佟泽友

(中国运载火箭技术研究院, 北京 100076)

0 引言

导引头是导弹的关键部件,导引头的建模品质会对制导性能的评估产生重要影响[1-2]。当前大部分导弹的导引头采用两框架平台式结构。导引头外框架轴通过轴承架在两个支架上,支架和底座固连在一起,力矩电机安装在轴的一端,以带动轴转动,电位计式测角器安装在轴的另一端,以测量外框相对机座的转动角度。内框架轴通过轴承架在外框架上,力矩电机安装在内框轴的一端,而电位计安装在另一端,探测器和双轴角速率陀螺安装在内框上,以测量弹目视线旋转角速度,提供制导信息[2-3]。

目前工程中对导引头动力学模型的认识仍不统一[4],当导引头带宽较大时,这种不一致会变得非常明显[5]。而当导引头模型使用不当时,会导致理论仿真与试验结果出现不一致[6],给设计分析工作造成了极大困扰。为从源头上解决问题,文中详细推导了导引头动力学方程,揭示了导引头隔离度产生的根本原因,并给出了设计用的导引头框图模型,可为工程应用提供理论参考。

1 坐标系及重要角度定义

1)弹体坐标系oxbybzb

弹体坐标系oxbybzb坐标原点取在导弹质心处,oxb轴与弹体纵轴重合,指向头部为正;oyb轴在弹体纵向对称面内与oxb轴垂直,指向上为正;ozb轴垂直于oxbyb平面,方向按右手直角坐标系确定。

2)外框坐标系odxgwygwzgw

外框坐标系odxgwygwzgw原点取在探测器中心,odxgw垂直于外框架平面,指向目标方向为正;odzgw轴与弹体坐标系的ozb轴平行,正向与ozb一致;odygw轴在oxbyb平面内,与其它两轴构成右手坐标系。该定义中外框为俯仰框。

3)内框坐标系odxgnygnzgn

内框坐标系odxgnygnzgn也可称作导引头坐标系,原点取在探测器的中心,odxgn轴与光轴指向重合,指向目标方向为正;odygn轴与odygw轴重合;odzgn轴在odxgwzgw平面,与其它两轴构成右手坐标系。该定义中内框为偏航框。

4)发射惯性坐标系oxyz

发射惯性坐标系oxyz原点取在发射点,ox轴在发射点水平面内,指向发射瞄准方向。oy轴垂直于发射点水平面指向上方。oz轴与其它两轴构成右手坐标系。

外框框架角φw:弹体坐标系oxb轴与外框坐标系odxgw轴之间的夹角,odxgw轴在oxb轴上方,则φw为正,反之为负。

内框框架角φn:内框坐标系odxgn轴与外框坐标系odxgw轴之间的夹角,odxgn轴在odzgw轴负向,则φn为正,反之为负。

两框架式平台导引头如图1所示。

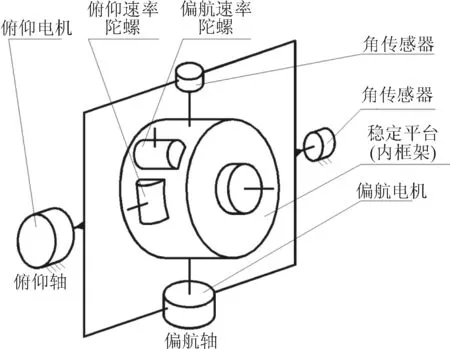
图1 框架式导引头结构

弹体坐标系向外框坐标系的转换矩阵:

外框坐标系向内框坐标系的转换矩阵:

弹体坐标系向内框坐标系的转换矩阵:

2 导引头框架动力学方程建立

(1)

(2)

把式(2)代入式(1),并投影到内框坐标系,可得:

(3)

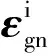
(4)

(5)

把式(5)代入式(4),并投影到外框坐标系,可得:

(6)

把式(6)代入式(3)中,可得:

(7)

对式(7)中的ωgnx、ωgnz进行求导得:

(8)

其中:

(9)

取内框架为研究对象,根据刚体定轴转动欧拉动力学原理,有:

(10)

(11)

把式(10)投影到内框架坐标系,代入式(8),有:

ωgnzHgny+(ρgnyagnz-ρgnzagny)mgn

(12)

ωgnxHgnz+(ρgnzagnx-ρgnxagnz)mgn

(13)

ωgnyHgnx+(ρgnxagny-ρgnyagnx)mgn

(14)

Mgny等于电机驱动力矩减去干扰力矩。干扰力矩包括粘滞阻尼力矩,弹簧力矩和库伦力矩,即:

(15)

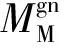
取外框架为研究对象,作用在外框架转动轴的合外力矩Mgwz为:

(16)

式(16)右边括号里的项即为内框对外框的反作用力矩,右边第一项为干扰力矩。

(17)

(18)

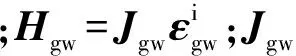
(19)

把式(18)投影到外框坐标系,将式(17)代入,有:

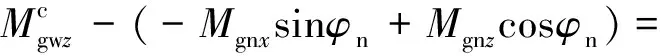
(20)

联立式(12)～式(14)、式(20),求解可得:

(21)

(22)

其中:

3 导引头动力学仿真框图

结合导引头测量控制过程,通过变换可得到两框架导引头动力学框图,如图2所示,图中qp为弹目俯仰视线角,qy为弹目偏航视线角,图中在导引头跟踪回路和稳定回路中加入了滞后校正网络以提高低频增益,降低导引头的稳态跟踪静差和隔离度。模型考虑了耦合力矩、干扰力矩和质量不平衡,可准确描述导引头的运动和控制过程,基于该模型可完成导引头回路的非线性仿真。

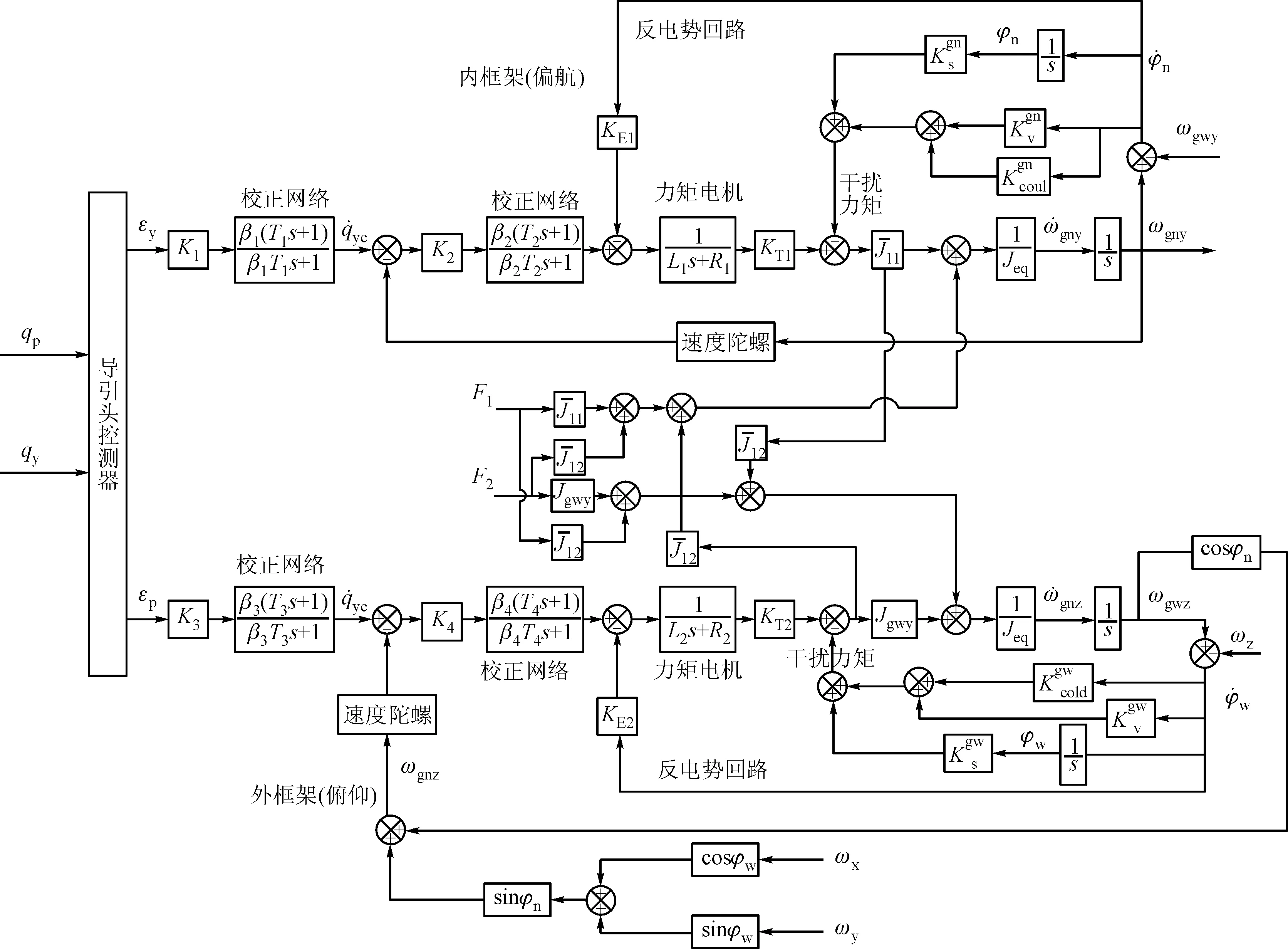
图2 导引头动力学仿真框图

由图2可知,弹体在导引头外框架轴正交方向上的扰动通过几何投影直接由内框架上的陀螺测量到,弹体在导引头外框架轴相同方向上的扰动通过干扰力矩影响外框架运动输出的形式,也由内框架上的陀螺测量到,这两者都是导引头隔离度的来源。

4 基于导引头动力学模型的仿真分析

4.1 隔离度特性仿真

4.2 耦合度特性仿真

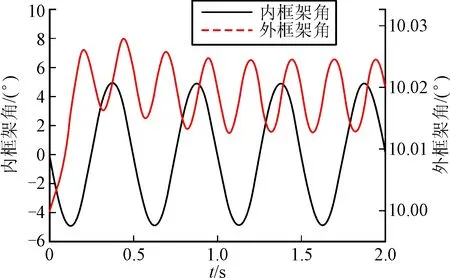
图4 导引头耦合响应

5 结论

文中完成了两框架平台式导引头建模,获得了导引头动力学模型,通过研究可得到如下结论:

a)导引头动力学基本方程是惯性系下的绝对角加速度的矢量方程,通过矢量投影得到了内、外框架的动力学方程;

b)导引头速率陀螺测量的是内框架在惯性系下的运动角速度在内框架上的投影值,并据此进行导引头伺服控制闭环,而不利用框架角和框架角速率等描述框架与弹体间相对运动的量进行闭环;

c)弹体在与外框架轴正交方向上的扰动通过几何投影直接由内框架上的陀螺感受,弹体在与外框架轴相同方向上的扰动通过干扰力矩影响外框架运动输出的形式,最终由内框架上的陀螺感受到,这是产生导引头隔离度问题的根源。

参考文献:

[1] QI Zaikang, XIA Qunli. Guided weapon control systems [M]. Beijing: Beijing Institute of Technology Press, 2004: 271-272.

[2] CHAUDHURY B, CHATURVEDIS. Study and optimization of plasma based radar cross section reduction using three-dimensional computations [J]. IEEE Transactions on Plasma Science, 2009, 37(11): 2116-2127.

[3] ZARCHAN Paul. Tactical and strategic missile guidance [M]. 5th editon Virginia: American Institute of Aeronautics and Astronautics, 2007: 143-144.

[4] 李富贵, 夏群利, 祁载康. 导引头隔离度寄生回路对最优制导律性能的影响 [J]. 航空学报, 2013, 30(12): 2658-2667.

[5] 杜运理. 导引头状态估计及隔离度影响研究 [D]. 北京: 北京理工大学, 2011: 82-100.

[6] 宋韬, 林德福, 祁载康. 平台导引头隔离度模型辨析 [J]. 北京理工大学学报, 2013, 33(6): 575-579.