一个《美国数学月刊》问题的证明与推广

郑 晨 周志俊 (邮编：241003)

安徽师范大学数学计算机科学学院

一个《美国数学月刊》问题的证明与推广

郑 晨 周志俊 (邮编：241003)

安徽师范大学数学计算机科学学院

本文证明了《美国数学月刊》上的问题11815, 并利用契比雪夫不等式和凸函数的性质给出了一个推广.

不等式; 契比雪夫不等式; 凸函数

《美国数学月刊》2015年第1期问题11815[1]如下

设x、y、z为正数, 且满足x+y+z=3, 试证:

≥3xyz.

①

本文给出了①的一个证明与推广.

=x2+y2+z2

=3xyz.

(2)

为了证明上述结论,先给出一个引理.

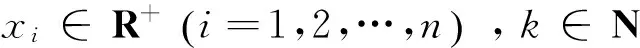
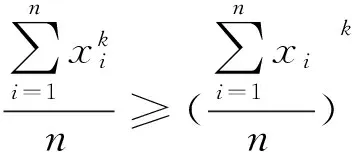
根据凸函数性质易证引理,下面证明定理.

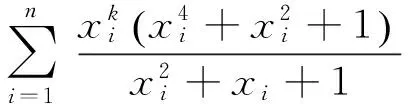
(利用契比雪夫不等式)

从而,定理得证.当n=3且k=0时,不等式②即为不等式①,故不等式②是不等式①的一个推广.

1GeorgeApostolopoulos.Problem11815[J].TheAmericanMathematicalMonthly, 2015, 122(1): 76

2 匡继昌.常用不等式(第三版)[M].济南:山东科学技术出版社,2004:62

2016-12-28)