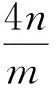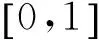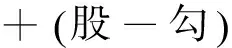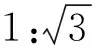几何概型
——悄然兴起的高考热点
2017-04-24邮编441000
王 勇 (邮编:441000)
湖北省襄阳市第一中学
复 习考 试
几何概型
——悄然兴起的高考热点
王 勇 (邮编:441000)
湖北省襄阳市第一中学
纵观近年高考试题及高考模拟试题,几何概型问题频频出现,这类问题新颖别致,构思精妙,极富思考性和挑战性.几何概型的概率求解一般分三步:①判断试验是否为几何概型;②将试验构成的区域和所求事件构成的区域转化为几何图形,并加以度量(如长度、面积、体积或角度);③应用几何概型的概率公式求概率.下面结合实例分类解析,旨在探索题型规律,揭示解题方法.
1 与长度有关的几何概型
例1 (2016·全国甲卷高考题文8)某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.某一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为( )
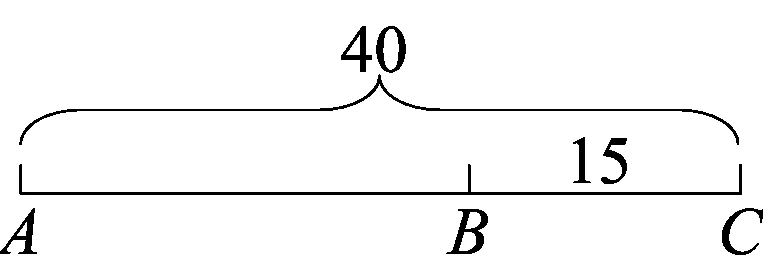
图1

点评 本题结合线段图考查与长度有关的几何概型.考查分析、解决实际问题的能力及运算求解能力.
例2 (2016·全国乙卷高考题)某公司的班车在7:30,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是( )
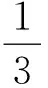
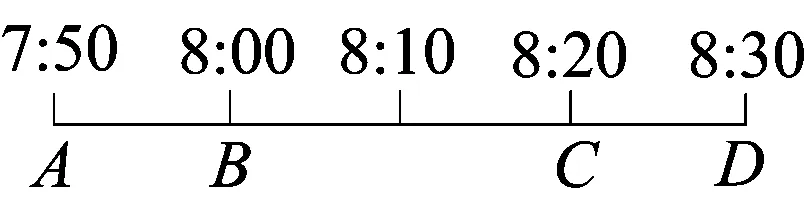
图2
解析 如图2,7:50至8:30之间的时间长度为40分钟,而小明等车时间不超过10分钟是指小明在7:50至8:00之间或8:20至8:30之间到达发车站,此两种情况下的时间长度之和为20分钟,由几何概型的概率计算公式知所求概率为
,故选
B
.
点评 本题结合线段图考查几何概型的概率计算公式.考查分析、解决实际问题的能力及运算求解能力.

解析 利用直线与圆相交的条件及几何概型求解.

点评 本题考查直线与圆的位置关系及几何概型.通过直线与圆相交求k的取值范围,考查转化与化归思想,通过求概率考查对几何概型概念的理解能力及运算求解能力.

解析 先利用对数函数的单调性解出不等式,再根据几何概型的概率计算公式求出概率.
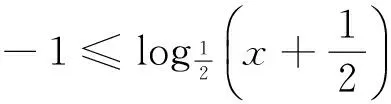
点评 本题考查对数函数性质的应用和几何概型.求解对数不等式考查了运算求解能力,几何概型概率的求解考查了创新应用意识.
例5 (2015·重庆市高考题)在区间[0,5]上随机地选择一个数p,则方程x2+2px+3p-2=0有两个负根的概率为______.
解析 先根据方程有两个负根求得p的取值范围,然后利用几何概型的概率计算公式求出概率.
因为方程x2+2px+3p-2=0有两个负根x1、x2,
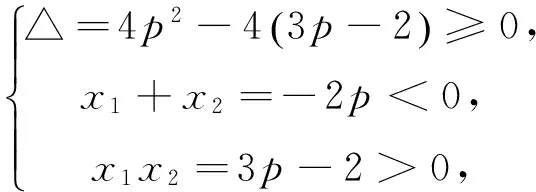
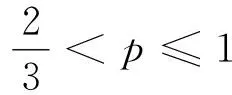
点评 本题考查一元二次方程根的分布和几何概型.根据一元二次方程根的分布情况建立不等式组,求p的取值范围,考查了逻辑思维能力与运算求解能力.将一元二次方程根的分布与概率相结合,体现了化归意识在解题中的应用.
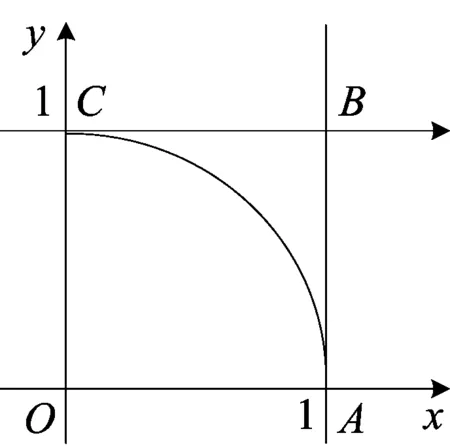
例6 (2016·长沙市模拟题)平面上画了一组彼此平行且相距2a的平行线.把一枚半径r 解析 设“硬币不与任一平行线相碰”为事件A. 图3 如图3,在两相邻平行线间画出与平行线间距为r的两平行虚线,则当硬币中心落在两虚线间时,与平行线不相碰. 点评 本题中把硬币不与平行线相碰转化为硬币中心到平行线的距离是关键,可方便地确定事件A的区域长度和所有可能结果的区域长度.将概率问题转化为几何问题来计算是几何概型的精华所在. 图4 解析 先求阴影部分的面积,再根据几何概型的概率计算公式求出概率. 点评 本题考查定积分的几何意义和几何概型.结合图形求解面积,考查了识图能力、运算求解能力和数形结合思想. 解析 根据复数的模构造出基本事件空间和随机事件对应的几何图形,转化为面积的比值. 点评 本题主要考查复数的模、几何概型以及直线与圆的位置关系等.通过将复数的模的关系式转化为圆面考查抽象概括能力,利用面积求几何概型的概率考查转化与化归思想、数形结合思想、运算求解能力及创新应用意识. A.p1 C.p3 图6 点评 本题考查约束条件表示的平面区域及几何概型.把问题抽象概括为几何概型问题求解,考查了转化与化归思想的应用.在比较概率大小时,考查了数形结合思想的应用. 例10 (2013·四川省高考题)节日前夕,小李在家门前的树上挂了两串彩灯.这两串彩灯的第一次闪亮相互独立,且都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以4秒为间隔闪亮.那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过2秒的概率是( ) 解析 结合线性规划,利用几何概型求解. 图7 点评 本题考查简单的线性规划和几何概型的应用.将实际问题转化为线性规划和几何概型问题求解,考查了转化与化归思想、创新应用意识以及运算求解能力. 图8 点评 本题考查奇函数及其性质,利用割补法求解商标区域的面积进而求解概率,充分彰显了数学的对称美、和谐美、简单美和奇异美.通过求概率考查数形结合思想和运算求解能力. 图9 例12 (2016·青岛市调考题)如图9,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1、D1C1上的点(点E与B1不重合),且EH//A1D1,过EH的平面与棱BB1、CC1相交,交点分别为F、G.设AB=2AA1=2a.在长方体ABCD-A1B1C1D1内随机选取一点,记该点取自于几何体A1ABFE-D1DCGH内的概率为p,当点E,F分别在棱A1B1、BB1上运动且满足EF=a时,则p的最小值为( ) 点评 本题由2010年福建省高考题改编而成,考查立体几何的有关知识、几何概型、基本不等式的应用等.考查空间想象能力、运算求解能力及“正难则反”的思想方法. 图10 点评 如果试验的全部结果所构成的区域可用体积来度量,那么就要结合问题的背景,选择好观察角度,准确找出构成事件A的区域体积及试验的全部结果构成的区域体积,再根据几何概型的概率计算公式计算即可. 例14 (2016·南昌市调考题)在圆心角为90°的扇形中,以圆心O为起点作射线OC,则使得∠AOC和∠BOC都小于30°的概率为______. 图11 点评 当涉及射线的运动,扇形中有关落点区域问题时,长以角的大小作为区域度量来计算概率,切不可用线段代替,这是两种不同的度量手段.作射线OD、OE,使∠AOD=30°,∠AOE=60°是求解本题的关键. 例15 (2016·宜昌市模拟题)在等腰Rt△ABC中,过直角顶点C在∠ACB的内部任意作一条射线CM交AB边于点M,则AM小于AC的概率为______. 分析 在∠ACB内的射线CM是均匀分布的,所以射线CM在∠ACB内的任何位置都是等可能的.因为AM的大小与点M在AB上的位置有关,为了确保AM 图12 解析 如图12所示,在AB上截取AC′=AC,连接CC′,则∠ACC′=∠AC′C,在△CAC′中,因为∠A=45°,所以∠ACC′=67.5°. 点评 解答本题时,要特别注意“在∠ACB的内部任意作一条射线CM交AB边于点M”这句话,由此确定“测度”是角度.如果把这句话改为“在线段AB上找一点M”,则问题的情境立刻发生改变,相应的“测度”应改为线段的长度. 图13 点评 本题考查几何概型及随机模拟.通过随机模拟的应用考查转化与化归思想,通过几何概型的计算考查数形结合思想和运算求解能力. 图17 内随机抛掷1000颗图钉,则落在黄色图形内的图钉数约为( ) A.866B.500C.300D.134 点评 本题以古代数学文化为背景考查几何概型的知识,既考查了考生对基础知识的掌握情况,又弘扬了中国古代优秀的数学文化.该题引导考生提高人文素养、传承民族精神,树立民族自信心和自豪感. 2016-12-26)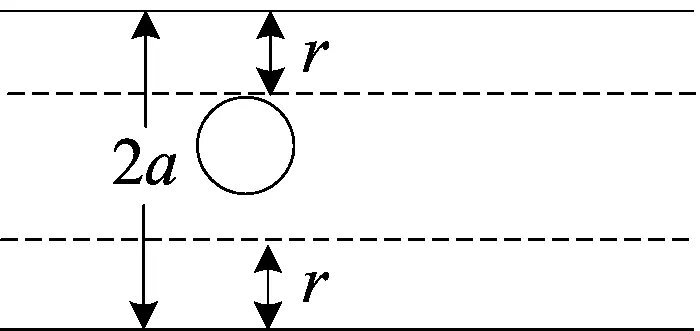
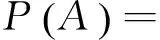

2 与面积有关的几何概型
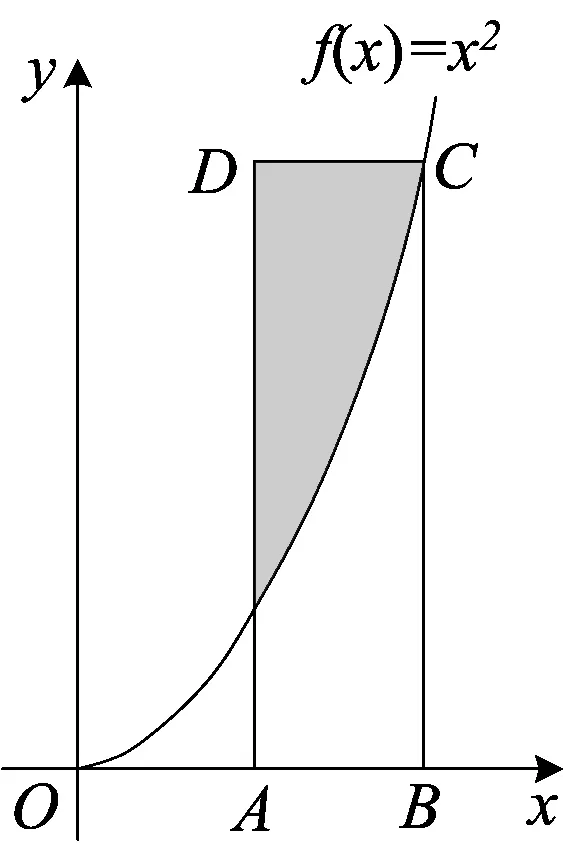

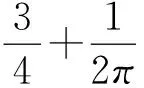

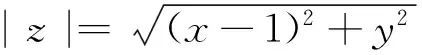


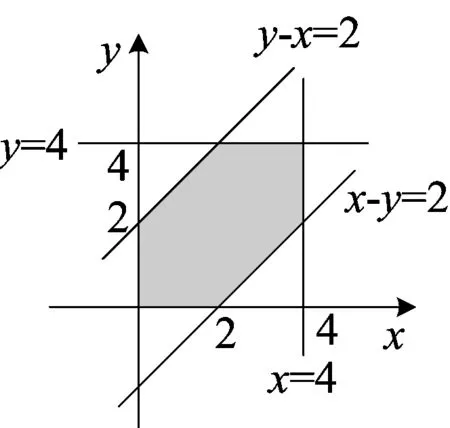

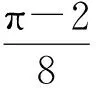

3 与体积有关的几何概型


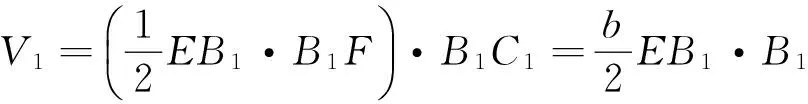
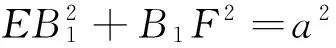





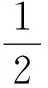

4 与角度有关的几何概型
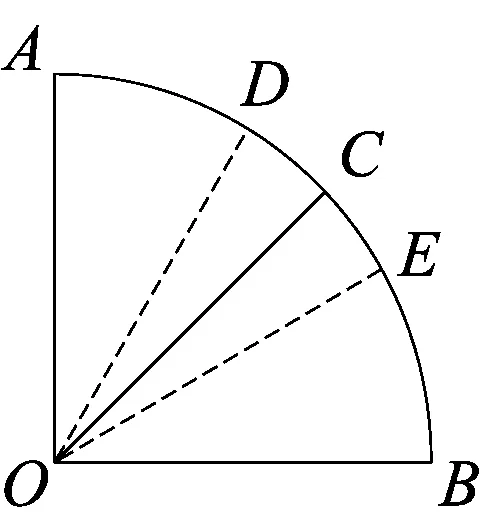
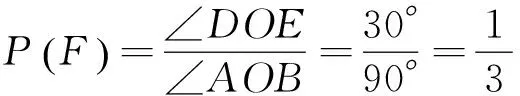

5 随机模拟问题