立足与立意并重 通法偕思想齐飞
——数学全国卷三角形试题的解答策略探析
2017-04-24李天霞邮编351200林新建邮编363000
李天霞 (邮编:351200)林新建 (邮编:363000)
福建仙游第二中学 福建漳州第一中学
立足与立意并重 通法偕思想齐飞
——数学全国卷三角形试题的解答策略探析
李天霞 (邮编:351200)林新建 (邮编:363000)
福建仙游第二中学 福建漳州第一中学
知识是载体,方法是手段,思想是灵魂,它们是知识体系的三个层次.
数学思想对于数学学习的作用是什么?
我们知道,人的行为源自于思想认识,思想的混乱必然会导致行为混乱,数学学习也是如此!
为什么有许多学生解决不了一些并不复杂甚至是简单的数学问题呢?除了极少数学生不知道相应的数学知识外,绝大部分不是不会方法,而是由于没有站在思想的高度来思考和引领方法,或者是因为思想不明确而想不起来用什么方法来处理问题.
比如解三角形,求解问题的通法是“知三求三”,即“已知三边求另外三个角,或已知两边一角求另一边和两角,或已知一边两角求另两边和一角”.
但在具体的问题情境中,如仅知一边和一角,这样就导致因条件不足无法直接运用“知三求三”这个通法予以求解,怎么办?
此时,若能立意于思想,如运用函数或方程思想引入变量凑足三个量,则可运用通法将三角形试题的解答进行得轻松自在!
下面以全国卷解三角形试题为例说明,以飨读者.
例1 (2011年高考新课标卷Ⅰ理科16题)
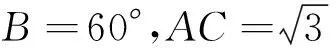
分析 本题仅知一边及其对角,条件不足无法直接运用通法予以求解,怎么办?
注意到本题是最值问题,若能立意于函数思想(最值问题必须构造出待求最值关于某个变量的函数,进而通过最值求解方法如配方法、导数法等将问题解决),则自然地想到去引入变量凑足三个量,这样就能运用通法将问题解决.
解析 设∠A=θ,则∠C=120°-θ.
例2 (2010年高考新课标卷Ⅰ文科16题)
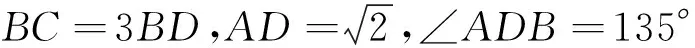
分析 本题也是三角形问题,无论在哪个三角形中,都是因为条件不足无法直接运用通法予以求解,怎么办?
注意到本题是变量求解问题,若能立意于方程思想(变量求解问题必须建立出关于待求变量的方程,进而通过解方程将问题解决),则自然地想到去设出变量凑足三个量,这样就能运用通法将问题解决.
解析 设BD=x,则DC=2x.

化简得:b2=2+4x2-4x.

化简得:c2=2+x2+2x.

例3 (2013年高考新课标卷Ⅰ理科17题)
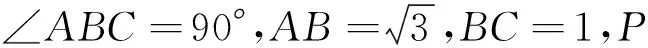
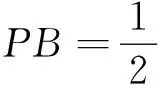
(2)若∠APB=150°,求tan∠PBA.
分析 本题难在第(2)问,同样已知一边及其所对角,无法直接运用通法求解,怎么办?
同样,本问是变量求解问题,故若能立意于方程思想,则自然地设出变量,这样就凑足了三个量,从而运用通法就能将问题解决了.
解析 设∠PBA=θ,则∠PBC=90°-θ.
在Rt△CPB中,因为BC=1,所以BP=BC·cos(90°-θ)=sinθ.


从以上的探析过程可以看出,数学全国卷三角形试题的解答需要立足于通法,也要立意于思想,只有立足通法与立意思想并重,才能使通法偕思想齐飞,将解三角形试题的解答“臻于完美” !
2016-12-29)
