一个三角形不等式的逆向
——兼擂题(109)的解答
2017-04-24褚小光,田开斌,潘成华等
一个三角形不等式的逆向
——兼擂题(109)的解答
1 背景
在△ABC中,有
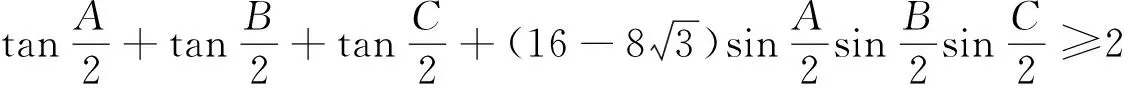
考虑上述不等式的逆向,我们提出了如下擂题(109).
在△ABC中,求证

2 证明
证法1 (文武光华数学工作室 褚小光 田开斌 潘成华提供)设s,R,r分别表示△ABC的半周长,外接圆与内切圆半径.根据三角形三角恒等式
所证不等式等价于

由Gerretsen不等式s2≥16Rr-5r2, 只需证
上式两边平方,约去r得
上式整理为


由欧拉不等式R≥2r,即知上式成立. 从而不等式得证.
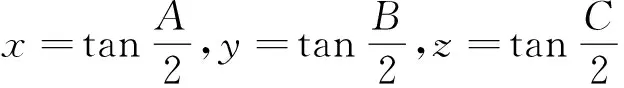
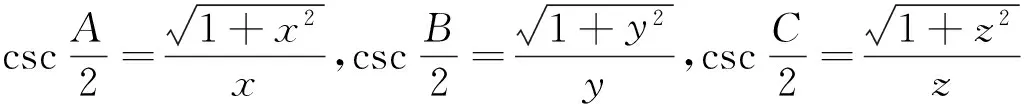
3∑x5(y3+z3)+6∑x4y4
+99∑x4yz(y+z)≥14∑x3y3z2
+214∑x4y2z2,
上式左边x,y,z的指数对右边形成优超,利用Muirhead定理知,上式成立,且等号成立当且仅当x=y=z,即三角形为正三角形.
万惠华老师指出,利用Muirhead定理,还可以证明擂题得的下列加强式:
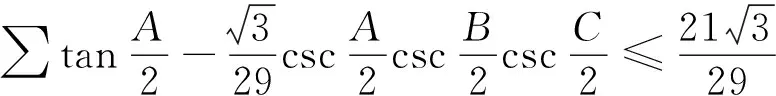
3 点评
(点评人郭要红,2017年3月31日)本论文收到擂题解答8份,其中5份是正确的,按时间顺序,作者分别是江斌(安徽,2017年2月25日),李歆(陕西武功县教育局教研室,2017年2月26日),光华工作室褚小光 田开斌 潘成华(江苏苏州,2017年2月27日),董林(山东高青县教学研究室,2017年2月28日),万惠华(浙江大学,2017年3月6日).李歆,董林的证明方法与证法1一致,江斌的证明是利用变换将擂题转化成代数不等式,利用柯西不等式等证明代数不等式成立. 本擂题得获奖者是江斌同志,请江斌同志看到评注后与编辑部联系.
1 陈计.关于三角形的一个不等式[J].中学数学,1995(3):34.
有奖解题擂台(110)
郭要红 (邮编:241003)
安徽师范大学数学计算机科学学院)
题 设R,r分别是△ABC中的外接圆半径,内切圆半径,则
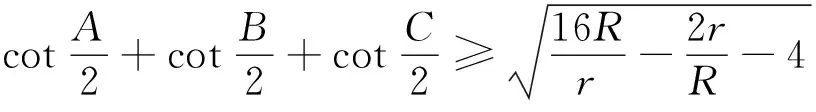
第一位正确解答者将获得奖金100元.
擂题及解答请电邮至guoyaohong1108@163.com, 解答时间以电邮时间为准.从2017年第一期开始,我们将连续刊载有奖解题擂台,欢迎广大读者踊跃提供擂题.
2017-01-05)
