涉及三角形傍切圆半径的一个不等式猜想的证明

姜卫东 (邮编：264210)

山东省威海职业学院信息工程系

初 数研 究

涉及三角形傍切圆半径的一个不等式猜想的证明

姜卫东 (邮编：264210)

山东省威海职业学院信息工程系

设△ABC的三边长分别为a、b、c，三边上的高为ha、hb、hc，傍切圆半径分别为ra、rb、rc，半周长为s，外接圆和内切圆半径分别为R、r，面积为△.

尹华焱老师在[1]中提出了100个涉及三角形Ceva线、傍切圆半径的不等式猜想，其中的第86个猜想为

HCX-86 在三角形△ABC中，有

①

本文将证明①成立.

证明 先证①左端不等式

应用柯西不等式可得

②

由三角形中的恒等式

ra+rb+rc=4R+r，

可知，欲证①左端不等式，只需证

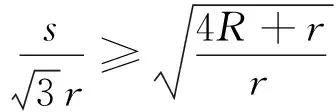
由Gerretsen不等式s2≥16Rr-5r2及欧拉不等式R≥2r，易知上式成立.从而①式左端获证.

下面证明①右端不等式

由已知的公式

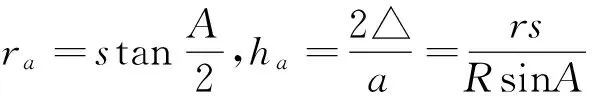
可知

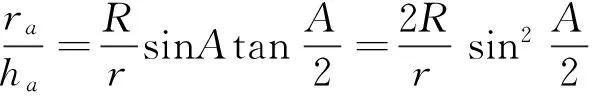
同理可得

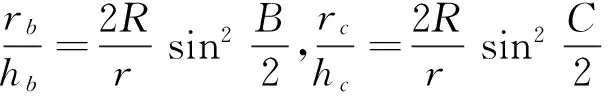
从而

③

注意到文[2](第130页,推论2.1.2)给出的不等式

④

由③和④立得②右端不等式.

注记1 由证明过程可知，如下更强的结论成立

⑤

⑤等价于如下不等式

⑥

注记2 2016年12月，安振平老师在其新浪博客中提出如下问题：

问题3347[3] 在△ABC中，a、b、c、R、r分别表示三边长，外接圆半径和内切圆半径，求证

⑦

1 尹华焱.100个涉及三角形Ceva线、傍切圆半径的不等式猜想[M]//杨学枝.不等式研究.拉萨：西藏人民出版社，2000:313-322

2 杨学枝，尹华焱.我国研究三角形中半角三角函数不等式情况综述。杨学枝。不等式研究，拉萨：西藏人民出版社，2000:123-174

3 安振平.问题3347：又一个三角形中的不等式，见(http://blog.sina.com.cn/s/blog_5618e6650102xbbd.html)

2016-12-20)