加肋圆柱壳结构的FE-BE算法网格尺度划分原则研究

黄振卫，周其斗，纪 刚，孟庆昌，段嘉希

(海军工程大学 舰船工程系，武汉 430033)

加肋圆柱壳结构的FE-BE算法网格尺度划分原则研究

黄振卫，周其斗，纪 刚，孟庆昌，段嘉希

(海军工程大学 舰船工程系，武汉 430033)

研究结构有限元耦合流体边界元算法(FE-BE算法)中结构湿表面的网格尺度划分原则具有十分重要的意义。以有限长加肋圆柱壳为研究对象，采用波数谱分析方法分离出结构主振型分量(携带能量最多的振动模式)。根据分析结果提出FE-BE算法中结构湿表面的网格尺度划分原则，并采用FE-BE算法验证了该原则的有效性。

加肋圆柱壳； 结构有限元耦合流体边界元； 振动与声辐射； 网格尺度

结构有限元耦合流体边界元(FE-BE)算法一直被认为是解决水下大型结构低频振动与声辐射的有力工具[1-3]，因为采用边界元方法求解无限域的声场问题时，边界元只需要在结构湿表面(结构物与水接触的表面)上划分，当结构有限元的划分完成后，边界元划分业已完成。为了节约FE-BE算法的计算成本，一般应选取单元尺度较大的有限元单元划分结构湿表面，但是这必然带来计算精度的降低。另一方面，为了保证FE-BE算法的计算精度，结构湿表面的单元尺度应该尽量小以便于描述最短的结构波长，但是这将导致大型复杂结构的边界元求解规模急剧地增加，使得FE-BE算法的计算时间非常长。因此，对于FE-BE算法，结构湿表面单元尺度的选取与计算精度和计算成本之间有个权衡的问题。目前很少有文献研究FE-BE算法中结构湿表面的网格尺度划分原则的问题。

结构的振动可以分解为一系列不同波长的振动分量的叠加，其中携带振动能量最大的分量即为结构的主振型分量。一般而言，采用有限元单元划分结构湿表面时，单元尺度必须要能够描述结构湿表面上最短的弯曲波长[4]，但是实际振动结构的最短弯曲波长可以无限小，如果采用非常小的单元尺度划分结构湿表面，将会使得系统的边界元求解规模急剧地增加。显然，不能简单地采用结构最短弯曲波长作为FE-BE算法中湿表面网格划分的参考标准。由于结构主振型分量的弯曲波长对于流固耦合计算精度有重要的作用，因此，本文重点采用波数谱方法分离有限长圆柱壳的主振型分量，根据分析结果提出FE-BE算法中结构湿表面的网格尺度划分原则，并采用FE-BE算法验证了该原则的有效性。本文首次提出了以结构主振型分量的弯曲波长作为FE-BE算法中结构湿表面的网格尺度划分的参考标准，结论对于FE-BE算法的有限元模型的网格划分具有十分重要的参考意义。

1 模型及有限元划分

以有限长加肋圆柱壳为研究对象，结构几何尺寸及材料和流体属性如表1所示。壳体内表面上均匀布置23根肋骨，激励力作用于中间肋骨上，沿着径向指向壳体外部的方向。采用有限元软件PATRAN进行建模，结构湿表面采用三角形单元进行有限元划分，肋骨采用四边形单元进行有限元划分，加肋圆柱壳的有限元模型示意图如图1所示。72个计算声场点均布于与柱壳中间肋骨同心，半径为9 m的圆周上。计算频率为50 Hz～500 Hz，频率间隔为5 Hz，模型为自由边界条件，不考虑自由水面对结构振动与声辐射的影响。

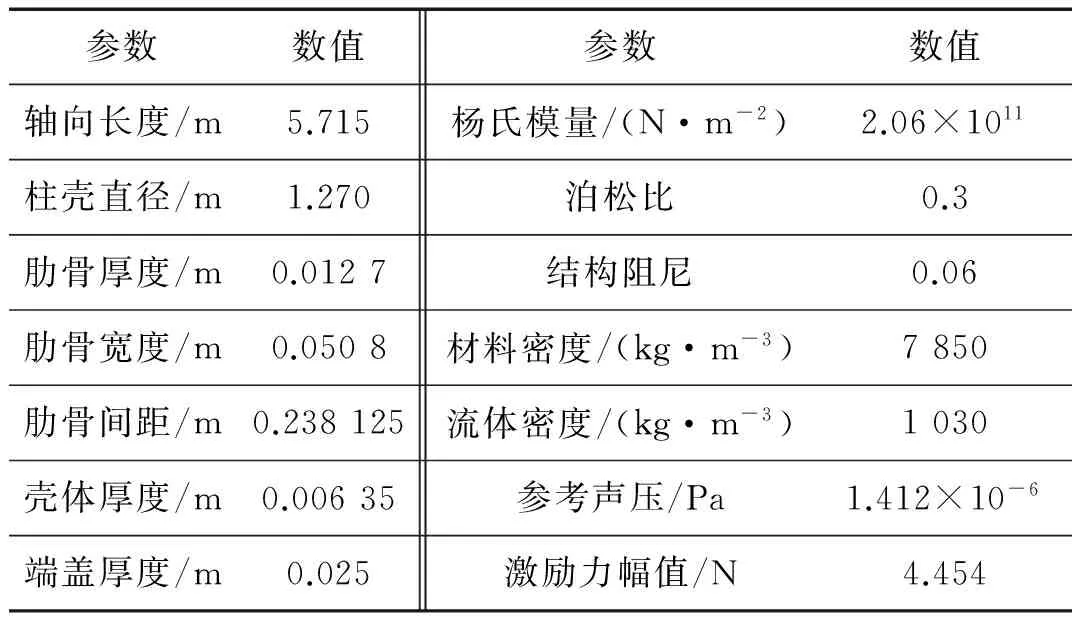
表1 模型几何尺寸及材料和流体属性Tab.1 Geometric size and parameter values for calculation

图1 加肋圆柱壳有限元模型Fig.1 Finite element model of the ring stiffened cylindrical shell

2 主振型的分离

本节采用编制的圆柱壳结构振动波数谱程序，分离柱壳结构主振型分量，该程序的正确性已在文献[5]中得到很好的验证。为了描述有限长圆柱壳结构做刚体运动的波数谱，将柱壳长度延长为原柱壳长度的12倍，假定延长的部分的外壳体法向速度为0[5]，如图2示，L为圆柱壳的长度，a为圆柱壳的半径，图中省略了肋骨示意。

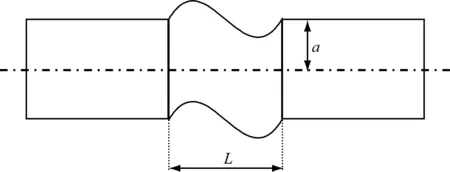
图2 无限长柱壳有限长模型Fig.2 An infinite length cylindrical shell with finite vibration distribution

采用编制的FE-BE算法程序计算圆柱壳湿表面的法向位移复数幅值w(z,θ)，即

(1)

式中：wR和wI分别为是结构湿表面法向位移的实部和虚部。值得注意的是，本节为了保证FE-BE算法程序计算结构湿表面振动响应的精度，加肋圆柱壳的每档肋骨间距采用6个单元进行划分，周向采用48个单元进行划分，最终得到15 552个结构单元，8 330个节点，14 448个湿表面单元，7 226个湿表面节点。

将法向位移的实部wR沿着柱壳的轴向和周向两个方向进行傅里叶变换，得到实部所代表的驻波场

(2)

式中，kz为轴向波数，n为周向完整波的数量，且有

(3)

(4)

同理，可以得到虚部所代表的驻波场

(5)

总的法向速度的振动功率可表示为

(6)

式中:Ev(n,kz)为法向速度振动功率谱，表达式为：

Ev(n,kz)=

(7)

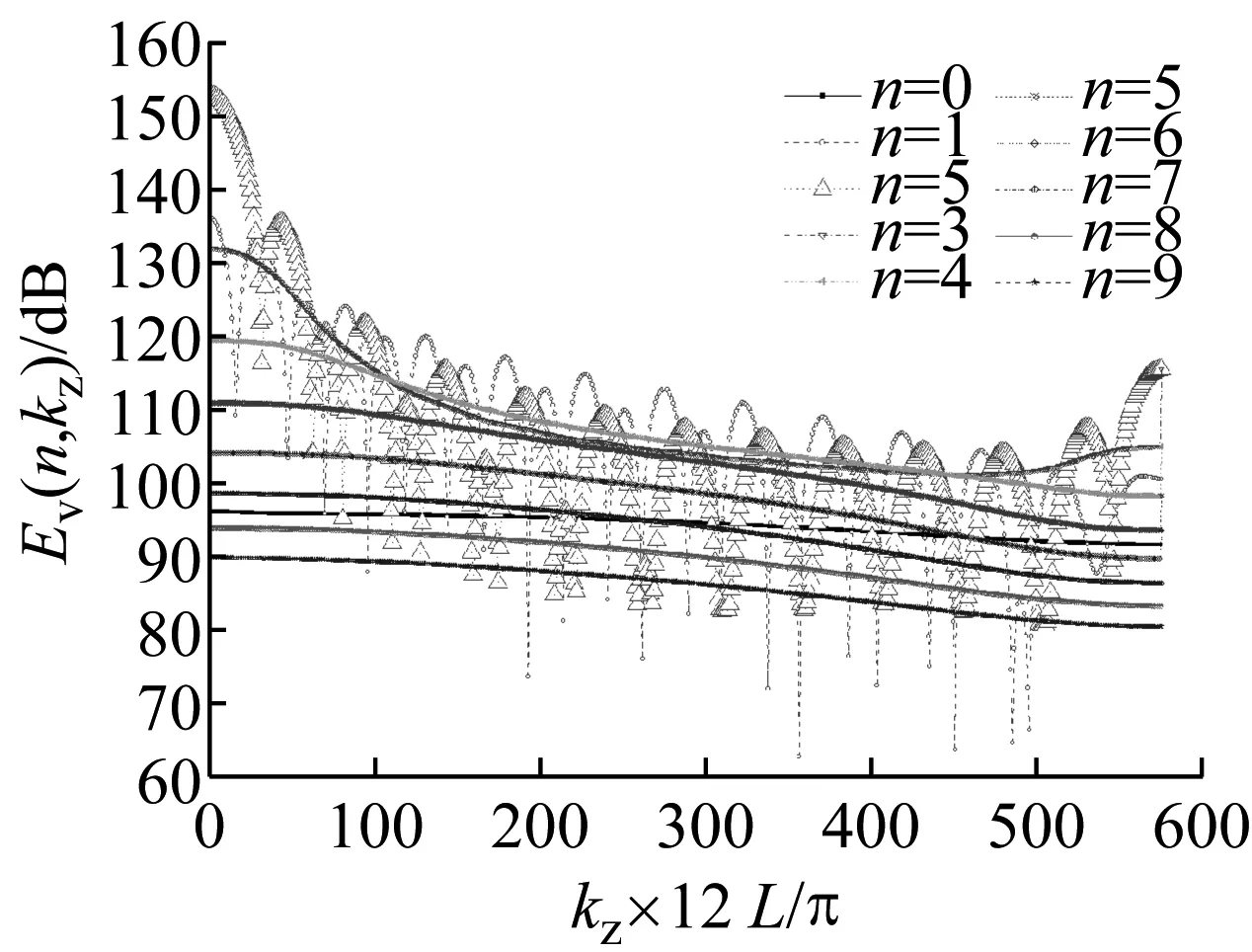
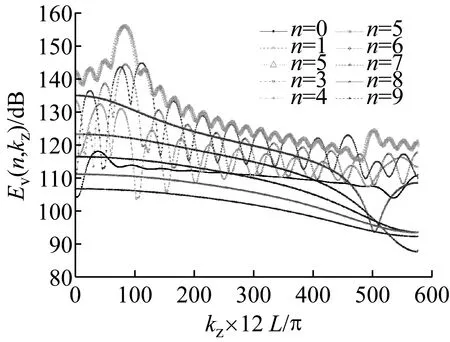
根据式(7)，即可绘制出不同的周向振动模式n时，结构法向速度振动功率随着结构轴向波数的变化曲线，进而分离出加肋圆柱壳的主振型分量以及主振型分量的弯曲波长λb。

图3为模型的法向速度振动功率谱(n=0,1,…,9)，从图3(a)中可以看出，当n=2，无因次轴向波数大约为0时，结构波的振动能量最大(主振型分量)，对应的结构轴向波长为∞。分析圆柱壳周向方向上结构波的传播特性，可以得到n=2时，周向上的结构波长为2πa/n=1.99 m。值得一提的是结构中其它非主振型分量携带的能量小于主振型分量所携带的能量，例如图3中振动能量级大3 dB，意味着携带的能量将增大一倍左右。

采用相同的方法即可分离出其他频率下结构主振型分量，计算结果见表2。

(a) 50 Hz

(b) 300 Hz

(c) 500 Hz

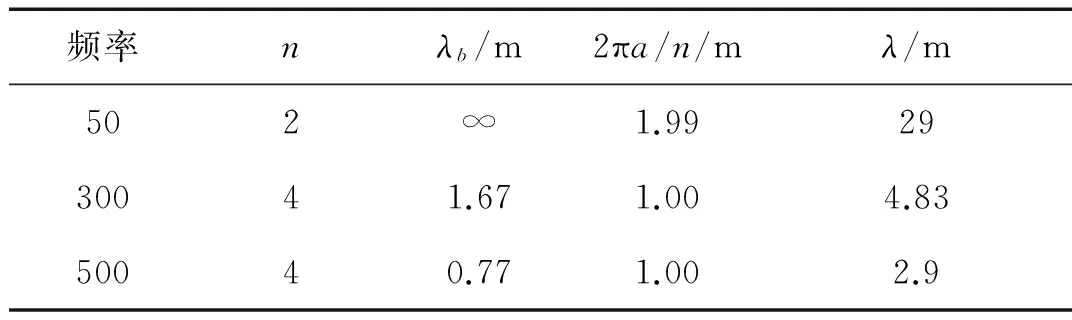
表2 不同频率下结构主振型分量Tab.2 Main vibration mode at different frequency

3 网格尺度对FE-BE算法的影响

由于加肋圆柱壳的振动与声辐射缺乏理论解，本文将逐步加密结构湿表面上的网格，观察FE-BE算法的计算结果是否趋于稳定，并与NASTRAN软件中的FE-IE算法[6]计算结果进行对比。为了保证无限元法的计算精度，在结构外域构造一个长10 m，半径5 m的圆柱面人工边界，人工边界的单元尺度为0.483 m，结构湿表面轴向单元尺度为0.059 m，周向单元尺度为0.083 m，无限元的计算阶数为10阶。根据第2节波数谱的计算结果，设计工况如表3所示。为了便于研究，所有工况下柱壳圆周方向上的单元尺度选取为Lc=0.083 m，定义Nz=λb/Lz为一个主振型波长内的单元数量，其中，Lz为结构湿表面轴向方向上的单元尺度，λb为结构主振型分量轴向弯曲波波长。

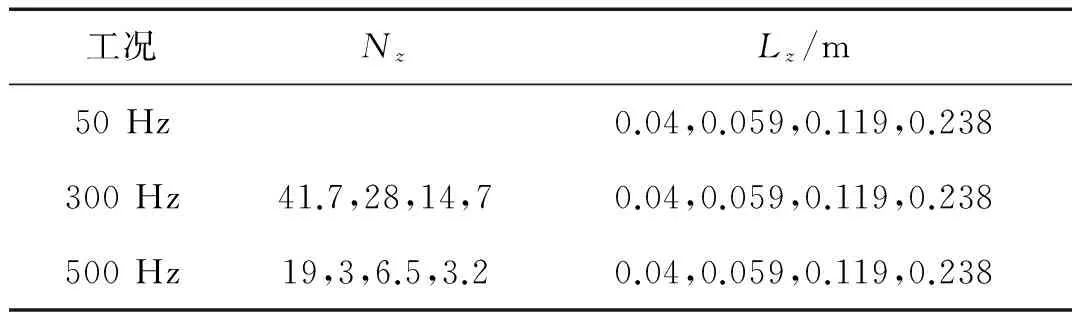
表3 计算工况Tab.3 Computational cases

图4～图6为各工况下辐射声压级的FE-BE算法计算值对比，从图中可以看出：

(1) 激励频率为50 Hz时，不同结构湿表面网格尺度下FE-BE算法的计算结果均与FE-IE算法的计算结果吻合良好。主要原因是，此时结构主振型的轴向弯曲波波长为无穷大，即使轴向单元尺度选取为一个肋骨间距一个单元(Lz=0.238 m)时，也能准确描述主振型分量的弯曲波波长。但是结构湿表面的单元尺度(即边界元尺度)不能无限增大，根据文献[7]，边界元的单元尺度一般应保证一个声波长至少有6个单元，因此，结构湿表面的单元尺度最大不能超过1/6倍声波长；

(2) 激励频率为300 Hz时，随着结构湿表面的单元尺度减小，FE-BE算法的计算结果趋于稳定，且与FE-IE算法的计算结果吻合良好。主要原因是300 Hz时FE-BE算法的结构湿表面网格尺度保证了一个主振型波长内至少有7个有限元单元，足以描述结构的主振型分量的波动特性；

(3) 激励频率为500 Hz时，随着结构湿表面的单元尺度减小，FE-BE算法的计算结果趋于稳定，但与FE-IE算法的计算结果有一定的差别。当结构湿表面的轴向单元尺度为Lz=0.238 m时，一个主振型弯曲波长内只有3.2个单元，无法准确地描述结构主振型分量的波动特性，因此，单元尺度为Lz=0.238 m的FE-BE算法计算结果与湿表面网格加密后FE-BE算法计算结果差别较大。当结构湿表面的轴向单元尺度为Lz=0.119 m时，保证了一个主振型弯曲波长内有6.5个有限元单元，此时FE-BE算法的计算结果与湿表面网格加密后FE-BE算法计算结果吻合良好。此外，500 Hz时网格加密后FE-BE算法计算结果与FE-IE算法计算结果产生一定差别的原因可能是近场效应对FE-IE算法的影响更为明显，为了改善FE-IE算法的计算精度，人工边界应该选取在距离结构湿表面更远的位置或者采用更小的单元尺度划分人工边界。

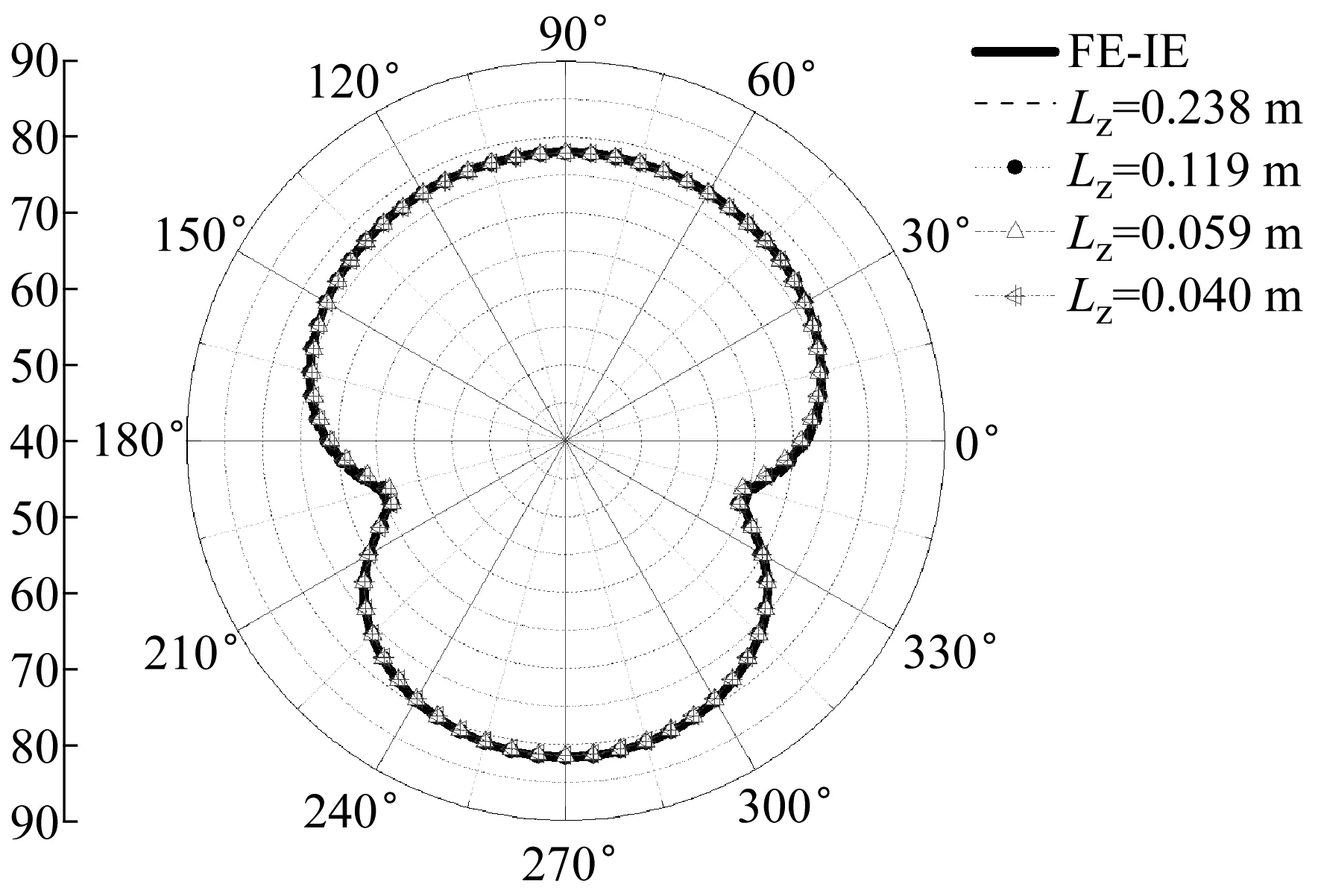
图4 加肋圆柱壳在50 Hz时的声压级Fig.4 Numerical SPL of the ring stiffened cylindrical shell at 50 Hz

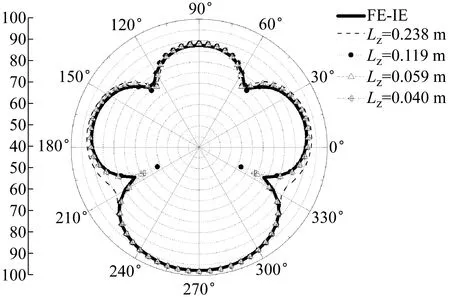
图5 加肋圆柱壳在300 Hz时的声压级Fig.5 Numerical SPL of the ring stiffened cylindrical shell at 300 Hz

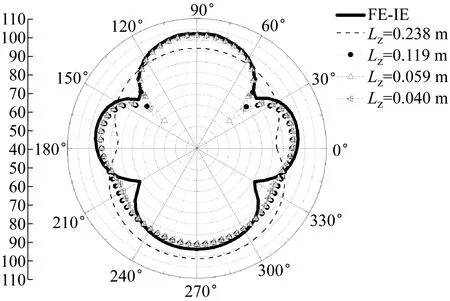
图6 加肋圆柱壳在500 Hz时的声压级Fig.6 Numerical SPL of the ring stiffened cylindrical shell at 500 Hz

总的来说，对加肋圆柱壳结构而言，当结构主振型分量的弯曲波波长小于对应激励频率下的声波波长时，以结构主振型分量的弯曲波长作为FE-BE算法中结构湿表面的网格尺度划分标准是可行的，即结构湿表面的网格尺度应保证一个主振型分量的弯曲波长内至少有6个单元。值得注意的是，此时结构湿表面的单元尺度能够描述结构中携带能量最大的振动分量，进而保证了FE-BE算法的计算精度。若将结构湿表面的单元尺度进一步减小或者增大，都有可能带来对应的计算成本的增加或计算精度的损失。

为了进一步应用FE-BE算法的网格划分原则，本节将计算50～500 Hz时外域声场中A(0 m,100 m,0 m)点的辐射声压级。根据以上分析，计算频率在500 Hz以内时，加肋圆柱壳每个肋骨间距采用2个单元进行划分(Lz=0.119 m)即可保证FE-BE算法的计算精度。同时，FE-IE算法中加肋圆柱壳每个肋骨间距4个有限元单元进行划分，人工边界为一个长12 m，半径为8 m的圆柱面，人工边界的单元尺度为0.48 m，无限元的计算阶次为10阶。A点的辐射声压级传递函数频响曲线如图7所示，从图中可以看出，激励频率较低时，FE-BE算法的辐射声压级传递函数频响曲线与FE-IE算法的频响曲线吻合良好；激励频率较高时，FE-BE算法的辐射声压级传递函数频响曲线与FE-IE算法的频响曲线变化趋势一致。

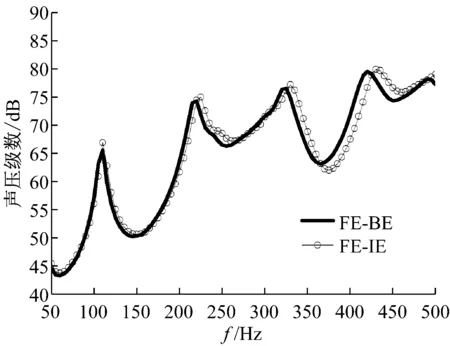
图7 结构声学传递函数的FE-BE计算值Fig.7 Sound transfer function obtained by the FE-BE method

4 结 论

本文重点采用波数谱方法分离圆柱壳结构的主振型分量，根据分析结果提出FE-BE算法中结构湿表面的网格尺度划分原则，并采用FE-BE算法验证了该原则的有效性，计算结果表明：对于文中算例而言，当结构主振型分量的弯曲波长小于对应激励频率下的声波长时，以结构主振型分量的弯曲波长作为结构湿表面的网格尺度划分标准是可行的，即结构湿表面的网格尺度应保证一个主振型分量的弯曲波长内至少有6个单元。

[1] ZHOU Q, JOSEPH P F.A numerical method for the calculation of dynamic response and acoustic radiation from an underwater structure[J].Journal of Sound and Vibration,2005(283): 853-873.

[2] 纪刚,张纬康,周其斗.静水压力作用的水下结构振动及声辐射[J].中国造船,2006,47(3):37-44.

JI Gang, ZHANG Weikang, ZHOU Qidou.Vibration and radiation from underwater structure considering the effect of static water preload[J].Shipbuilding of China,2006,47(3):37-44.

[3] EVERSTIN G C, HENDERSON F M.Coupled finite element/boundary element approach for fluid-structure interaction[J].J.Acoust.Soc.Am., 1990,87:1936-1947.

[4] 宗福开.波传播问题中有限元分析的频散特性及离散化准则[J].爆炸与冲击,1984,3(4):16-23.

ZONG Fukai.Frequency dispersion characteristic and discretization of the finite element analysis in wave propagation problems[J].Explosion and Shock Waves,1984,3(4):16-23.

[5] 谭路.基于波数谱的细长壳体圆柱壳振动与声辐射噪声特性研究[D].武汉：海军工程大学，2013.

[6] 田丽思,李相辉,马越峰,等.MSC Nastran 动力分析指南[M].北京：中国水利水电出版社,2012.

[7] KIM J K, IH J G.Prediction of sound level at high-frequency bands by means of a simplified boundary element method[J].Journal of the Acoustical Society of America, 2002,112(6): 2645-2655.

Principle to select element size of FE-BE algorithm for a ring stiffened cylindrical shell

HUANG Zhenwei, ZHOU Qidou, JI Gang, MENG Qingchang, DUAN Jiaxi

(Department of Ship and Engineering, Naval Univ.of Engineering, Wuhan 430033, China)

Investigating the principle to select element size of structural wet surface in the FE-BE algorithm has a great significance.The structural bending wavelength of the main vibration mode of a finite length ring stiffened cylinder was computed with the wave number spectrum method to provide some principle for selection of element size of a structural wet surface.Numerical computation showed the effectiveness of the principle.

ring stiffened cylindrical shell; FE-BE algorithm; vibration and sound radiation; element size

国家自然科学基金(51309230)

2015-10-27 修改稿收到日期：2016-02-19

黄振卫 男，博士生，1986年生

周其斗 男，教授，博士生导师，1962年生

TH1

A

10.13465/j.cnki.jvs.2017.05.023