用圆孔内单边裂纹平台巴西圆盘和实验-数值-解析法确定砂岩的动态起裂和扩展韧度

周 妍，张财贵，王启智,3

(1.四川大学 土木工程及应用力学系，成都 610065； 2.湖南工学院 建筑工程与艺术设计学院，湖南 衡阳 421000;3.水力学及山区河流开发保护国家重点实验室，成都 610065)

用圆孔内单边裂纹平台巴西圆盘和实验-数值-解析法确定砂岩的动态起裂和扩展韧度

周 妍1,2，张财贵1，王启智1,3

(1.四川大学 土木工程及应用力学系，成都 610065； 2.湖南工学院 建筑工程与艺术设计学院，湖南 衡阳 421000;3.水力学及山区河流开发保护国家重点实验室，成都 610065)

在I型(张开型)动态断裂实验中，利用大直径(∅100 mm)分离式霍普金森压杆径向冲击圆孔内单边裂纹平台巴西圆盘试样。考虑了材料惯性效应和裂纹扩展速度对动态应力强度因子的影响，用实验-数值-解析法确定了高加载率和高裂纹扩展速度情况下，砂岩的动态起裂韧度和动态扩展韧度。由动态实验获取试样的动荷载历程，采用裂纹扩展计(Crack Propagation Gauge，CPG)测定试样断裂时刻和裂纹扩展速度，获得裂纹扩展速度对应的普适函数值。然后将动荷载历程带入到有限元软件中进行动态数值模拟，求出静止裂纹的动态应力强度因子历程，再用普适函数值对其进行近似修正。最后根据试样的起裂时刻和穿过CPG中点的时刻，由相应的动态应力强度因子历程分别确定砂岩的动态起裂和动态扩展韧度，它们分别随动态加载率和裂纹扩展速度的提高而增加。

圆孔内单边裂纹平台巴西圆盘；实验-数值-解析法；动态起裂韧度；动态扩展韧度；裂纹扩展计；普适函数

动态断裂的研究一直受到工业过程和军事行动的密切关注，如深部采矿，隧道开挖，高边坡失稳,流星撞击，导弹穿甲，地震冲击，爆破和恐怖袭击等，最近更有提议用爆炸冲击波代替水力压裂以提高油页岩气的产量[1]。断裂动力学的最早经典性文献要追溯到MOTT[2-3]1948年发表的论文，大量研究表明动荷载作用下的断裂行为完全不同于静荷载作用的情况。断裂动力学是研究惯性效应不能忽略的那些断裂力学问题，这些问题一般分为两类：① 动荷载作用下裂纹的起裂；② 裂纹的快速扩展与止裂。岩石的动态断裂韧度是表征岩石抵抗裂纹动态起裂和动态扩展的基本力学参数，研究其测试方法十分重要。

测试试样采用圆孔内单边裂纹平台巴西圆盘[4](Holed Single Cracked Flattened Brazilian Disc, HSCFBD)，这种试样构型有一定优点。国际岩石力学学会提出了四种测试岩石静态断裂韧度的建议试样[5-6]，有人字形切槽三点弯曲圆棒试样、人字形切槽短圆棒试样、人字形切槽巴西圆盘(Cracked Chevron Notched Brazilian Disc, CCNBD)试样和切槽半圆盘三点弯曲试样(Notched Semi-Circular Bend, NSCB)[7]。岩石动态断裂韧度的测试方面，多采用分离式霍普金森压杆(Split Hopkinson Pressure Bar, SHPB)作为加载装置，常用的试样分为三类：①巴西圆盘类试样；②弯曲类试样和③紧凑拉伸类试样[8]。其中巴西圆盘类试样通过对径压缩产生间接拉伸作用以测量岩石等准脆性材料力学参数[9]，试样加工相对容易，实验时无需额外夹具固定，加载方便。原始巴西试验的缺点是由于施力点的应力集中使起裂点发生在接触点(或弧面)而不是圆盘的中心, 解决此问题的途径有两个：增加平台[10]，增加圆孔[11]，或两者皆有[12]。综上所述，圆孔内单边裂纹平台巴西圆盘和圆孔(内双边)裂纹平台巴西圆盘是比较理想的测试岩石断裂韧度的构型。二者的优点是：① 是圆盘类试样，可以压缩致拉，不需要额外夹具；② 圆孔和平台的存在削弱了加载点应力集中的影响，保证试样在预制裂纹处起裂。③ 应力波在圆环型试样边界反射时间比较长，使裂纹面不受到复杂应力波的影响。樊鸿等[13]用应变片法对圆孔(内双边)裂纹平台巴西圆盘混凝土试样进行了动态起裂时间的研究，张盛等[14]采用圆孔(内双边)裂纹平台圆盘确定岩石的动态起裂韧度。但动态断裂问题比较复杂，单边裂纹消除了两个裂尖的相互影响，方便进行相关的分析。

实验-数值-解析法是一种新的测试方法。由于边界的一部分(裂纹)在运动，裂纹的扩展与止裂问题是一个高度非线性问题，现有的理论分析是在做了很多特殊假定下才得出的[15-18]，目前数学理论还不足以解决断裂扩展的一般问题。岩石动态断裂韧度的确定方法可以分为直接测定法和间接测定法两种。直接测定法是直接测量动态实验过程中试样全场或裂尖奇异区的应力应变，然后利用裂尖奇异区应力应变的理论分析进行反推以确定动态应力强度因子的方法，主要包括光学测试方法和应变片法。DALLY等[19]使用光弹法测量动态应力强度因子，并研究了动态应力强度因子和裂纹扩展速度之间的关系。宋义敏等[20]采用数字图像相关法作为试验的观测手段，对岩石I型裂纹在冲击荷载作用下的动态断裂进行了试验研究。JOUDON等[21]利用应变片法确定了较广的裂纹扩展速度范围内Ⅰ型张开裂纹的动态应力强度因子。光学测试方法需要有高速摄影，对测得的图片精度和图片分析要求很高，高昂的消费也不适用于岩石动态断裂试验。应变片法贴片时要满足位置和角度要求，裂纹需要按理想路径平直扩展，试验条件很难达到。间接测定法则是在实验中仅获取试样的动态加载历程等易于测定的信号，然后借助已有公式或者数值模拟的方式进行应力应变分析以确定动态应力强度因子的方法，主要包括准静态法和实验-数值法。DAI等[22]研究了人字形切槽半圆盘三点弯曲试样，采用准静态法测定了花岗岩动态起裂韧度，并从能量角度确定了岩石的动态扩展韧度；ZHANG等[23]用SHPB装置对切槽半圆盘三点弯曲试样加载，采用准静态方法得到了大理岩的动态起裂韧度和动态扩展韧度；GAO等[24]采用切槽半圆盘三点弯曲试样，分别利用准静态法和数字图像相关法对花岗岩的动态起裂韧度和动态扩展韧度进行了研究。苟小平等[25]通过对径冲击CCNBD试样分别对砂岩的I型动态起裂韧度进行了实验数值法和准静态法的对比；WANG等[26]用SHPB装置径向撞击中心直裂纹平台巴西圆盘试样，采用实验-数值法得到了不同加载率下大理岩I型和II型的动态起裂韧度；杨井瑞等[27]采用实验-数值法结合普适函数的方法，用无平台的中心直裂纹巴西圆盘试样得到了砂岩的动态断裂韧度；张财贵等[28]同样采用实验-数值法结合普适函数的方法，用边裂纹平台圆环试样测试岩石的I型动态断裂韧度。准静态法认为最大荷载值对应的应力强度因子即为材料的动态断裂韧度，忽略了惯性效应的影响以及试样实际起裂时间是否与最大动荷载对应的问题，故不适用于高速加载情况。实验-数值法把试验重点放在了动态荷载历程和数值模拟上，降低了对实验设备的苛刻要求，并且通过动态数值模拟考虑了惯性效应的影响。但是对于运动的裂纹，裂纹长度和裂纹传播速度都是未知函数，考虑到裂纹尖端的奇异性，很难用有限元分析模拟出裂纹扩展的情况。如何处理裂纹扩展速度对动态应力强度因子的影响是一个关键问题。在实验-数值法的基础上提出了实验-数值-解析法。引入了普适函数对数值计算获得的动态应力强度因子进行近似解析修正。普适函数是由POPELAR等[29-30]基于Green函数基本解的概念，通过对无限大线弹性体半无限匀速扩展裂纹表面受时间无关荷载作用的裂纹问题理论推导所得，又随后推广至裂纹以任意速率扩展和受一般荷载作用的情况。普适函数体现了裂纹扩展速度在不超过Rayleigh波速时对动态应力强度因子的影响，即：在任何情况下，张开裂纹在一般荷载作用下以任意速度v扩展的动态应力强度因子KI(v)等于瞬时裂尖的普适函数值k(v)乘上适用于具有该处静止裂纹的相同荷载下的动态应力强度因子，这对于I型扩展裂纹是普遍适用的。ROSAKIS等[31]在对高应变率下脆性失效本构关系的微观力学研究中用相应静止裂纹的准静态应力强度因子和裂速普适函数值的乘积得到了动态应力强度因子；REN等[32]根据数值模拟的结果和应用普适函数提出了PMMA材料动态断裂过程中裂纹速度和动态断裂能之间的关系；MARKUS等[33]通过数值模拟和理论分析研究了裂纹扩展的路径特征和极限速度；谢和平等[34]利用普适函数修正了岩石断裂分形路径上扩展裂纹的动态应力强度因子。目前为止，光学测试方法、应变片法等多用于测试动态起裂韧度。要测试动态扩展韧度，必须考虑裂纹扩展速度对它的影响。通过普适函数对数值计算结果进行近似解析修正，不需要很复杂的实验和分析就解决了该问题。

本次实验使用∅100 mm大直径SHPB装置径向冲击外半径75 mm的圆孔内单边裂纹平台巴西圆盘试样。SHPB广泛用于岩石材料的动态试验研究[8]，是研究材料在中高应变率(102～104s-1)下力学性能的主要实验方法，是爆炸与冲击动力学实验技术的重要组成部分[35]。宋义敏等[28]采用可调速落锤冲击试验机作为试验加载装置进行了I型动态断裂试验研究，文献[35]通过对比，说明落锤加载装置会使应力波效应影响加载的测量，也不能实现高应变率加载。选用大尺寸试样可以减小试样内部细微颗粒和缺陷对动态断裂韧度测试结果的影响。通过裂纹扩展计(Crack Propagation Gage, CPG)对试样的起裂时刻以及裂纹扩展速度进行检测[36]。CPG在实验过程中仅占用一个数据采集通道，克服了在预期的裂纹扩展路径上粘贴一系列应变片的测速方法占用通道数较多的缺点[37]，同时也避免了粘贴多枚应变片时造成的误差，使测得的起裂时刻和扩展速度更加准确。考虑到材料的惯性效应对动态应力强度因子的影响，把实验获得荷载历程加载到有限元模型中。对数值计算获得动态应力强度因子用普适函数进行近似解析修正，考虑了裂纹扩展速度对动态应力强度因子的影响。采用实验-数值法-解析法简单有效地获得了砂岩在不同加载率下的动态起裂韧度和不同裂速下的动态扩展韧度。

1 动态断裂实验的数据采集和分析

1.1 圆孔内单边裂纹平台巴西圆盘试样制备

试样选用笔者提出的圆孔内单边裂纹平台巴西圆盘(HSCFBD)。试样由四川隆昌青砂岩岩芯制作而成，其颗粒细致、紧密，均匀性良好。试样加工(如图1所示)分为4个基本步骤：① 选用厚度为50 mm厚的石板，通过∅150 mm套筒切割成圆盘。② 用C6132A车床将圆盘加工成内径∅30 mm圆环。③ 用旋转的合金刀头在圆环径向加工一对平行的平台。④ 用旋转的金刚砂铣刀在圆孔边径向预制一条6 mm的切槽。再采用打磨成厚0.3 mm的钢锯条进行精加工，裂尖宽度小于0.4 mm，符合ISRM关于岩石试样裂纹尖端宽度制作要求，消除了预制裂纹宽度对试验的影响。

(a)加工圆孔(b)加工圆盘(c)加工内单边裂纹

图1 HSCFBD试样加工过程

Fig.1 Processing of HSCFBD specimen

该砂岩杨氏弹性模量E=17.67 GPa，泊松比μ=0.21，密度ρ=3 055 kg/m3，膨胀波波速cd=2 551.6 m/s，畸变波波速cs=1 546.0 m/s，Rayleigh波波速cR=1 411.0 m/s。

图2(a)和图2(b)分别为HSCFBD几何构型简图以及加载状态的实物图，其中试样外半径R=75 mm；内孔半径r=15 mm；厚度B=50 mm，平台角2β=20°，初始裂纹长度a=6 mm。

1.2 SHPB加载装置

动态实验加载装置为∅100 mm大直径SHPB，2014年2月在解放军总参谋部洛阳工程兵科研三所常规武器侵彻爆炸效应防护实验室中完成。SHPB材料为42CrMo，弹性模量Eb=210 GPa，泊松比为0.3，密度为7 850 kg/m3，一维纵波理论波速为5 172 m/s。SHPB直径为Db=100 mm，入射杆长li=4 500 mm，透射杆长lt=2 500 mm，入射杆上的应变片SGi到试样-入射杆接触端的距离为l1=1 500 mm，透射杆上的应变片SGt到试样-透射杆接触端的距离l2=1 000 mm，SHPB加载系统，如图3所示。

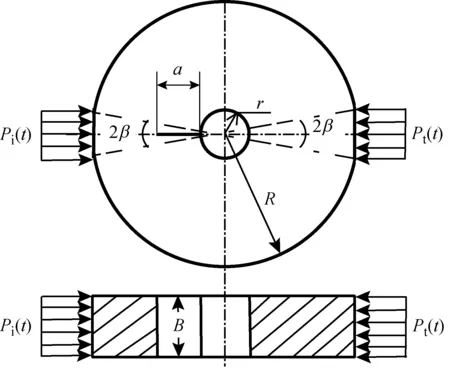
(a) HSCFBD试样几何构型

(b) HSCFBD试样加载实物图

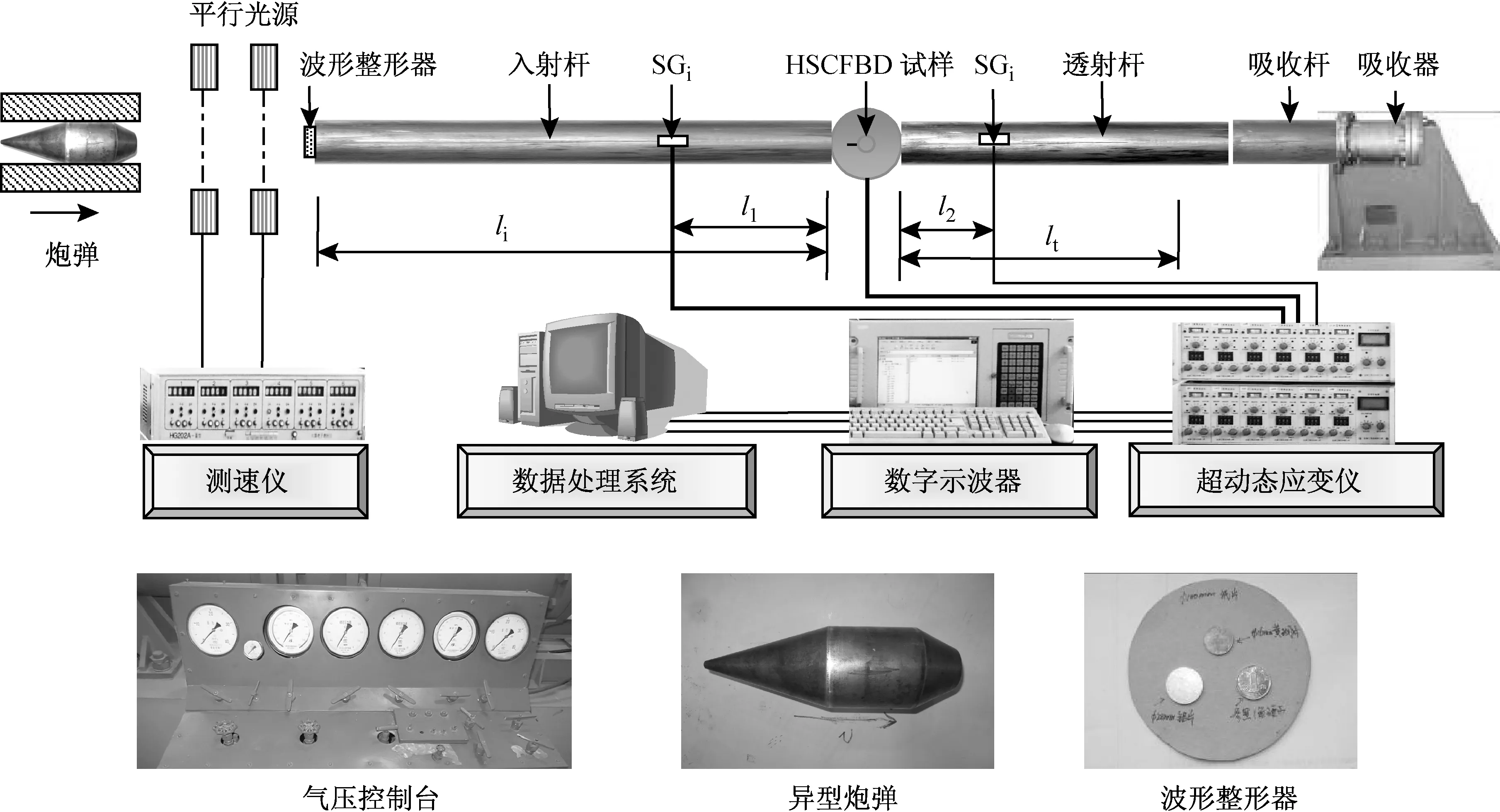
图3 SHPB加载系统Fig.3 Loading system of SHPB

实验时，通过气压控制台来控制弹膛气压，进而调节炮弹速度，炮弹出膛速度由光电测速装置测量。当气炮驱动炮弹撞击入射杆，在入射杆中会产生高速弹性压缩波，通过入射杆传播到达试样，一部分反射回到入射杆中，一部分通过试样使其沿预制裂纹方向开裂，另一部分透射进入透射杆。入射杆和透射杆上的应变信号由超动态应变仪转化为电压信号后由数字示波器采集显示出来，采集频率为10 MHz，采集长度为40 K，即4 096 μs内采集40 960个数据点。

岩石颗粒较粗且试样内部不可避免的含有少许细微缺陷，所以岩石试验通常采用较大的尺寸，相应地的需要增大SHPB的直径，而杆径的增加会使波形弥散问题加重。通过对矩形波、三角波和半正弦波的比较，正弦波在传播过程中基本无弥散。刘德顺等[38]提出了半正弦波是SHPB装置合理加载波形的概念。LOK等[39]根据冲击反演理论得到了能产生理想正弦应力波的炮弹形状。为了便于加工和试验操作对理想炮弹形状进行简化，形成“圆台-圆柱-圆台”的异形炮弹，炮弹实物图，如图3所示。

为拉长加载波波形上升沿和过滤加载波中由于直接碰撞引起的高频振荡成分，在炮弹与入射杆的撞击端粘贴波形整形器(黄铜片、铝片或硬纸片，如图3)。通过对比使用3种波形整形器时SHPB空打获取的波形，发现硬纸片能够有效改善加载波波形，因此正式实验中采用硬纸片作为波形整形器。

摩擦是决定所有压缩实验是否有效的重要因素[40]。为了降低试样加载端面摩擦的存在，在试样与SHPB装置压杆的接触面均匀涂抹了少量凡士林作为润滑剂。

1.3 试样两端动荷载的确定

入射杆上的应变片SGi和透射杆上的应变片SGt分别用来记录加载时的入射应变εi(t)、反射应变εr(t)和透射应变εt(t)。试样HSCFBD-06实验过程中入射杆和透射杆上的信号，如图4所示。

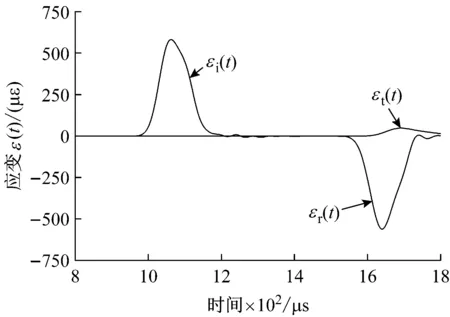
图4 入射杆和透射杆上的应变信号Fig.4 Strain signal of incident bar and transmission bar

图4所示的应变信号可能开始时不在零点，所以要先对其进行飘零处理。对波形前段平缓阶段取平均值H，让波形整体减去H，其后找到波峰A点，取1/5峰值点B以及点B前后各5点的平均斜率确定一条直线，该线与时间轴交与点C，继而找到应力波的波头点D，试样HSCFBD-06的入射波波头确定[41]，如图5所示。由于动态实验的重点是试样受荷载作用以后的时间段，因此定义加载波到达试样入射端面的时刻t0为零时刻。在分别确定入射波和反射波的波头ti、tr后，由t0=(ti+tr)/2即可确定试样入射端受到荷载作用的时间，试样中用到的其它时间均减去t0后运用。

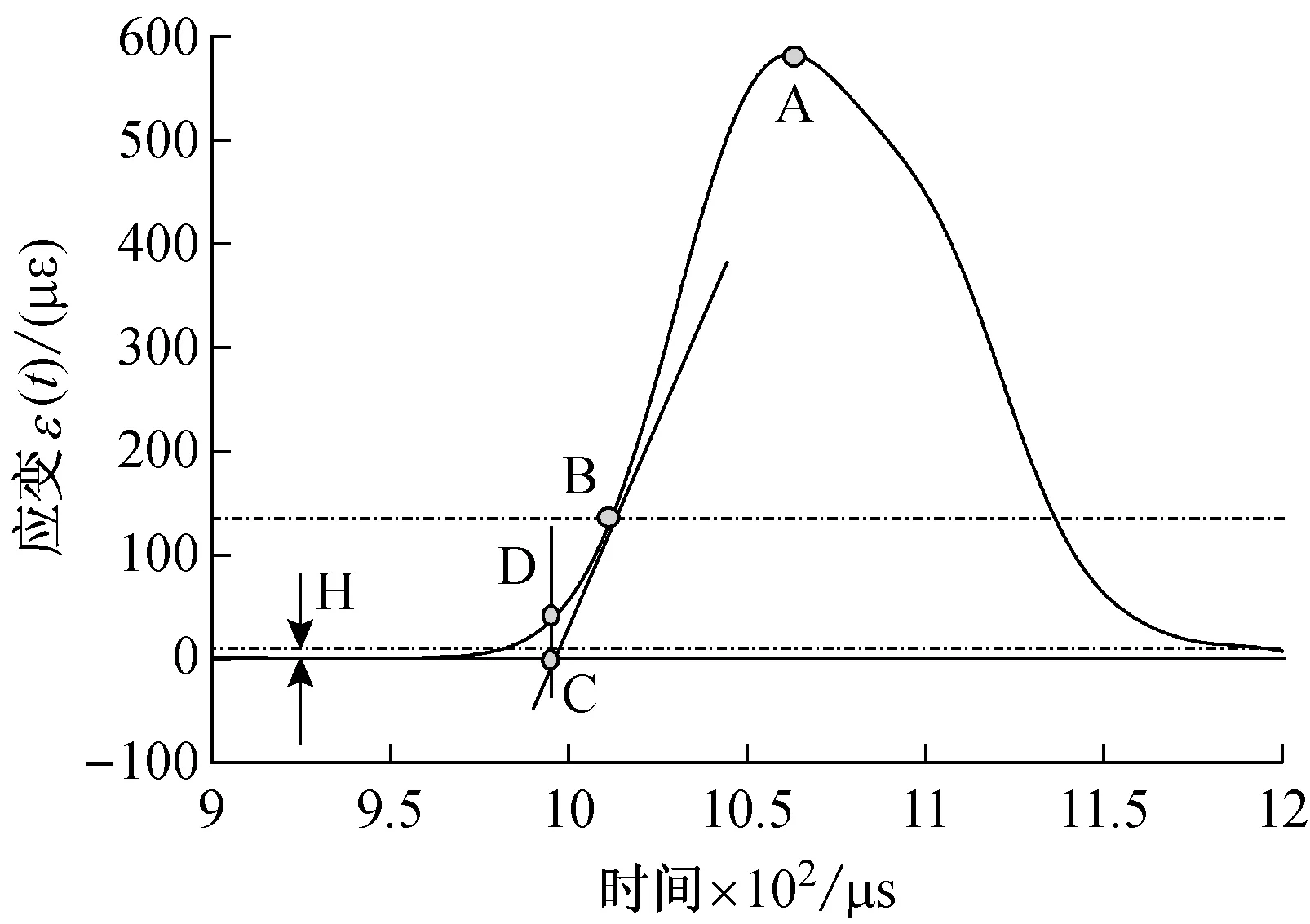
图5 HSCFBD-06试样入射波波头的确定Fig.5 Determination of incident wave-head of HSCFBD-06

根据SHPB实验技术的一维弹性应力波假设，由入、反射波的叠加可以得到入射杆对试样入射端的作用力Pi(t)，由透射波可以计算得到透射杆对试样透射端的作用力Pt(t)，分别如式(1)、(2)所示。

Pi(t)=EbAb[εi(t)+εr(t)]

(1)

Pt(t)=EbAbεt(t)

(2)

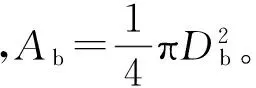
试样HSCFBD-06入射端和透射端的荷载时程曲线，如图6所示。各试样荷载的相应信息，见表1。

试样入射端的动态荷载一般有三种选取方式：一波法P1(t)、二波法P2(t)和三波法P3(t)。P1(t)即为透射端荷载Pt(t)，P2(t)即为入射端荷载Pi(t)，P3(t)即为P1(t)和P2(t)的平均值。

一切固体材料都是有惯性和可变形性，当受到随时间变化的外荷载作用时，它的运动过程是一个应力波传播、反射和相互作用的过程。固体静力学忽略惯性是允许忽略或者没有必要研究这一到达静力平衡前的应力波传播和互相作用过程，只关注应力平衡后的结果。在动态加载条件下，荷载以应力波形式在试样中传播，要忽略惯性效应，达到应力平衡状态就要求应力波在试样内部的传播时间t可以忽略且试样两端的动荷载幅值基本相等。应力平衡条件下，入射端和透射端荷载是基本等价的，则三种波形叠加方式获得的荷载应该比较接近。从图6中也可看出本次实验试样透射端的动荷载P1(t)与入射端的动荷载P2(t)相比出现了明显地峰值减小和上升沿拉长的现象，说明应力不平衡。应力不平衡会造成三种方法确定的荷载有较大不同。由文献[42]可知，P2(t)要更接近试样入射端的真实荷载。

1.4 裂纹扩展计测定起裂时刻和裂纹扩展速度

采用CPG测定HSCFBD试样入射端裂纹的起裂时间和扩展速度。CPG的型号为BKX5-4CY，初始电阻约为2 Ω，由玻璃丝布基底和卡玛铜敏感栅组成，其中敏感栅由10根等长但粗细不同因而电阻不同的电阻丝并联而成。CPG的敏感栅沿裂纹扩展方向长度为l=10 mm，相邻两根电阻丝之间距离l0=1.11 mm，垂直于裂纹扩展方向的宽度为h=5 mm，见图7。在HSCFBD试样上粘贴CPG时，应使裂纹预期扩展路径尽量垂直通过各栅丝的中点处，并且最接近裂纹尖端的电阻丝R1阻值最小，距离裂尖最远处的电阻丝R10阻值最大。

CPG电路连接，如图7所示。采用型号为APS3005Dm的恒压源(C.V.source)提供20 V恒压，CPG与电阻RC2=50 Ω并联，并联后的电路再与大电阻RC1=1 076 Ω串联。由于恒压源在输出微小的电压时容易出现电压波动，采用在CPG两端并联小电阻之后再串联大电阻的方法，既可以保证恒压源本身能够稳定的输出较大的电压，又能够保证CPG两端的分压不至过大而影响使用精度或者超过其额定功率而损坏。

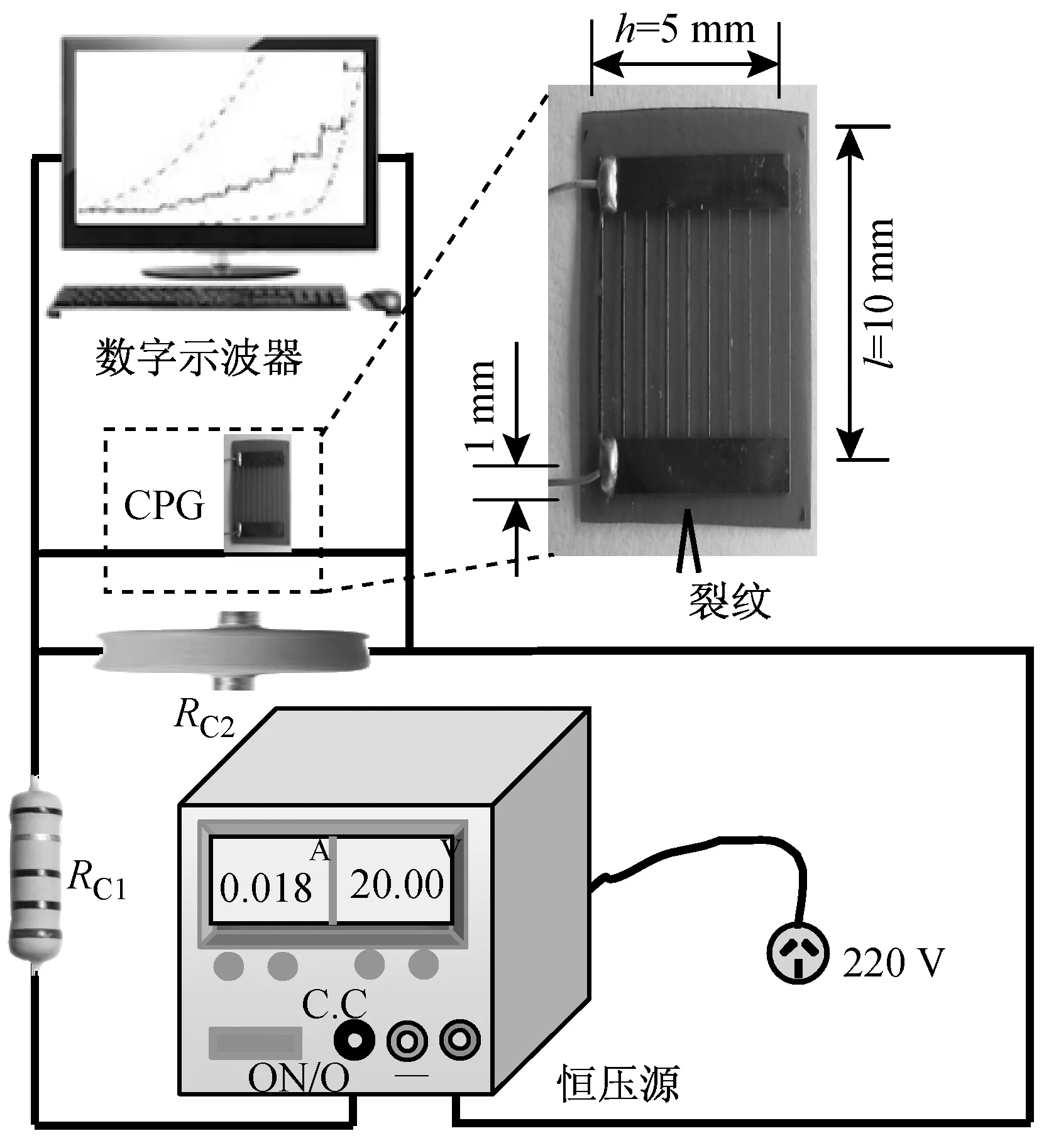
图7 裂纹扩展计电路图Fig.7 Circuit diagram of crack propagation gauge (CPG)

当试样裂纹向前扩展，穿过CPG第m(m=1，2，…，10)根电阻丝所在位置导致相应电阻丝断裂时，CPG和RC2的并联总电阻会相应地产生突变，使CPG两端的电压呈现阶梯状突变，故而在实验中可以根据CPG两端电压信号的变化判断裂纹尖端所达到的位置，从而获得裂纹起裂时刻和扩展速度。电阻的变化量

m=1,2,…,10

(3)

试样HSCFBD-06的CPG电压信号以及电压对时间导数如图8所示，电压呈阶梯状上升，10个台阶的突变时刻对应CPG上相应电阻丝的断裂时刻。根据电压对时间的导数峰值所对应的时刻可以准确地确定CPG上对应10根电阻丝的断裂时刻t1～t10以及相邻两根电阻丝间的断裂时间差值Δti。相邻两根电阻丝之间距离l0=1.11 mm，裂纹在CPG测量范围内的扩展速度vi=l0/Δti(i=1，2，…，9)。

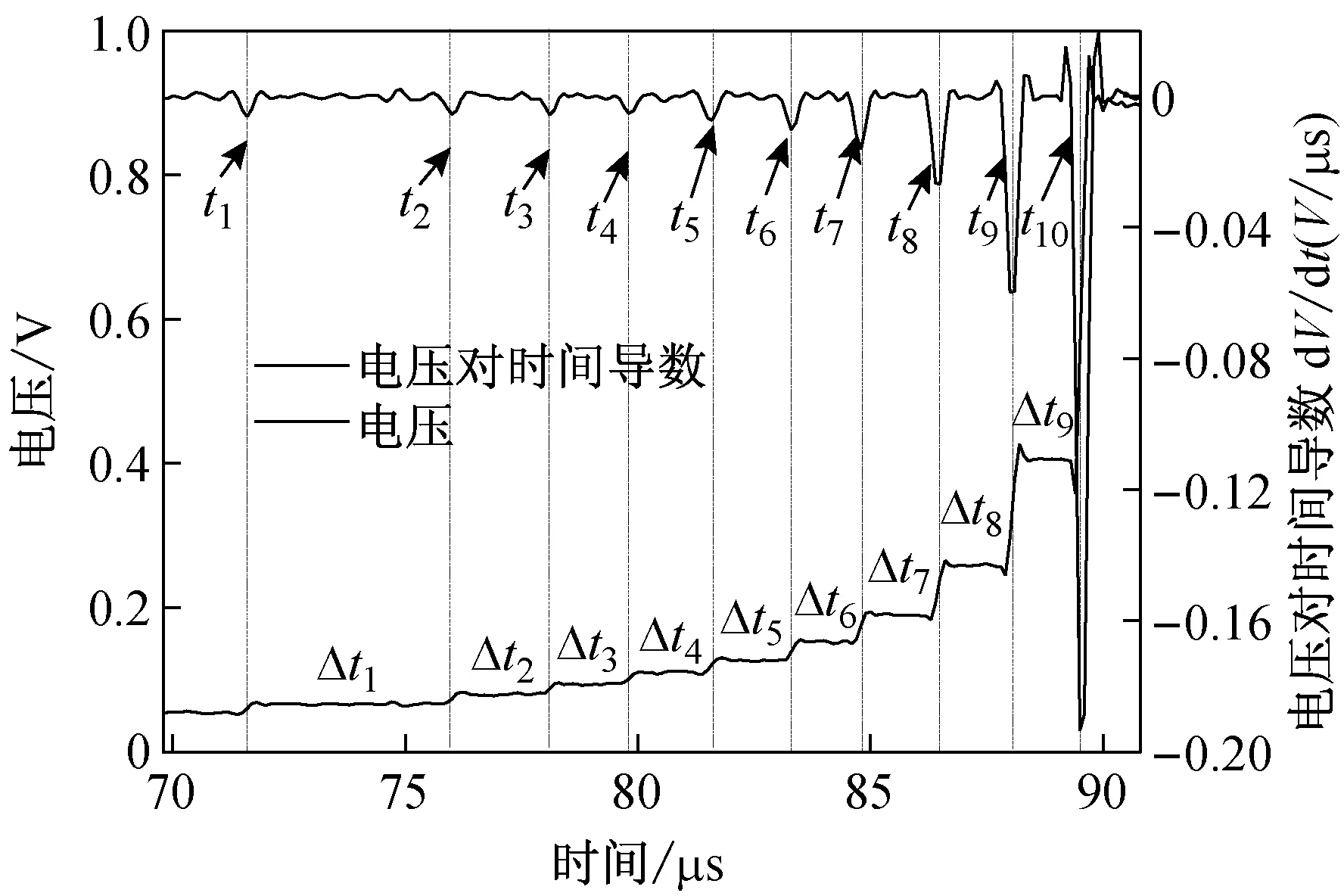
图8 HSCFBD-06试样上CPG两端电压以及电压对时间导数Fig.8 Voltage and its derivative w.r.t time for the CPG on HSCFBD-06 specimen

HSCFBD-06试样的裂尖所到达的位置、扩展速度与时间的关系如图9所示。试样的最大扩展速度vmax=785.71 m/s，最小速度vmin=251.72 m/s，平均速度va=483.1 m/s。从图9中可以看出，裂纹开始起裂速度比较小，扩展速度有一定程度的上下动荡，这种现象主要和岩石本身的不均匀性以及裂纹高速扩展时更容易产生曲折的裂纹扩展路径有关，如图10所示。但CPG整个测量范围内裂纹扩展速度却基本保持在平均速度的水平，因此我们假定试样在tf=t1时刻起裂以后，扩展的裂纹以速度va匀速穿过CPG测量区域，并以平均速度va作为裂纹tp=(t1+t10)/2时刻扩展至CPG中点处的裂速代表值。各试样起裂时间tf、平均扩展速度va及裂纹穿过CPG中点的时刻tp，见表1。

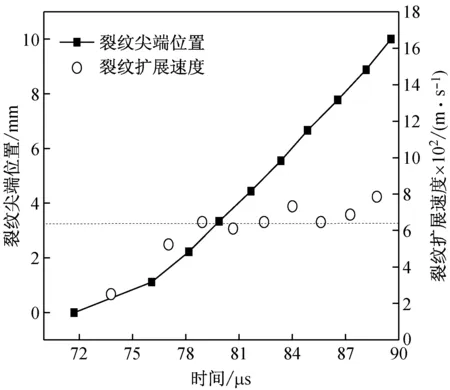
图9 HSCFBD-06试样的裂尖位置以及裂纹扩展速度Fig.9 Crack tip position and crack propagation velocity of HSCFBD-06 specimen

图10 裂纹高速扩展时的扩展路径Fig.10 High speed crack propagating path

2 数值计算确定静止裂纹的动态应力强度因子历程

2.1 HSCFBD数值模型

为确保本文动态有限元计算结果的精度，首先对经典的“Chen问题”[43]进行了有限元分析，并和Chen的有限差分结果进行了对比，两者所得的动态应力强度因子时程曲线非常吻合。在此基础上，根据HSCFBD试样的对称性采用有限元软件ANSYS建立1/2平面模型，如图11所示。模型采用PLANE82平面应变单元，采用1/4节点奇异单元表征裂纹尖端应力场和应变场的奇异性(如图12)，时间子步步长设置为0.1 μs，模型共有2 230个单元和6 897个节点。把实验获得的动态荷载加载到试样入射端，将试样透射端设置为固定约束。试样静止裂纹的动态应力强度因子通过位移外推法[25]由式(4)计算获得。

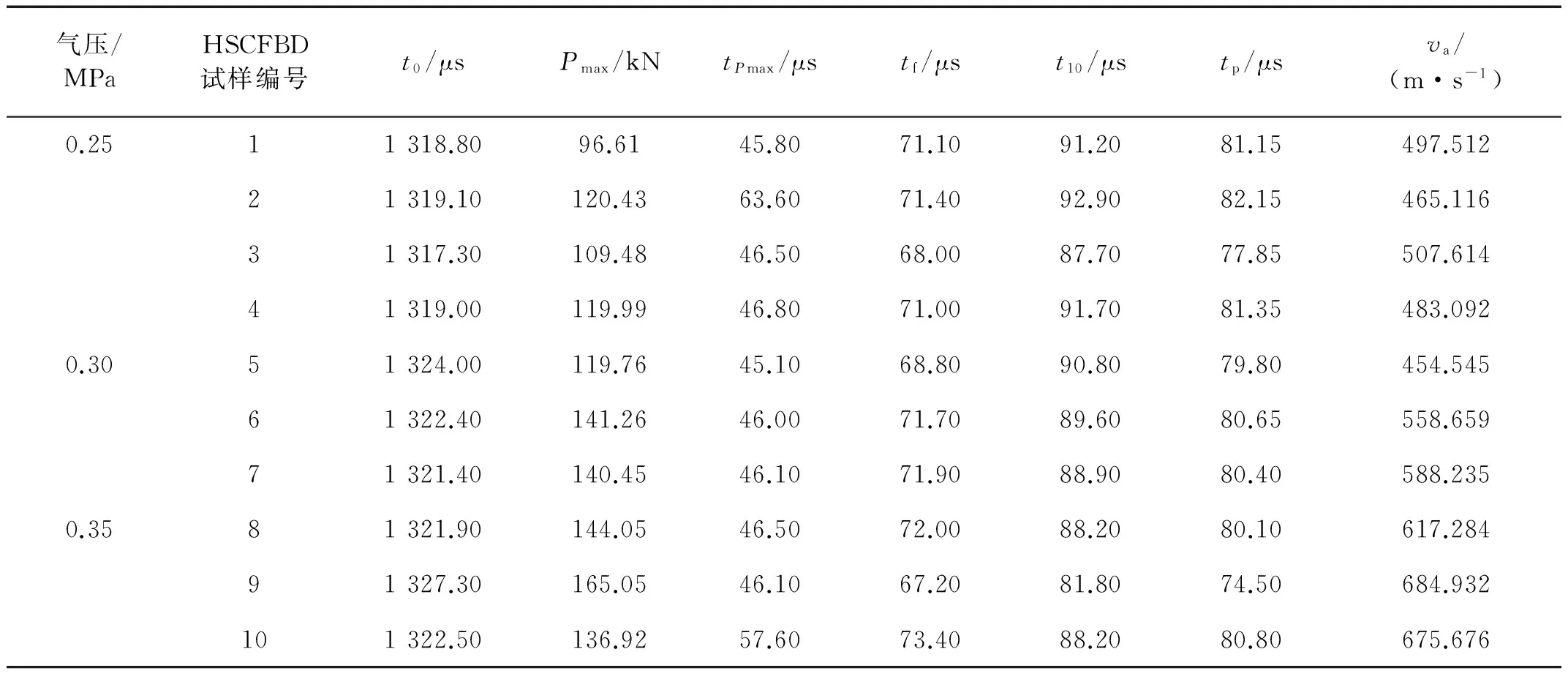
表1 HSCFBD试样实验数据Tab.1 Experimental data of the HSCFBD specimens

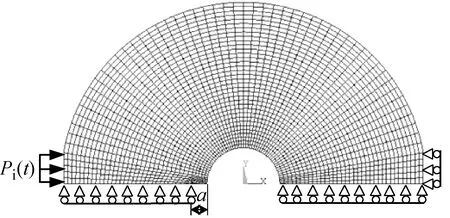
(a) HSCFBD裂纹起裂前的有限元模型

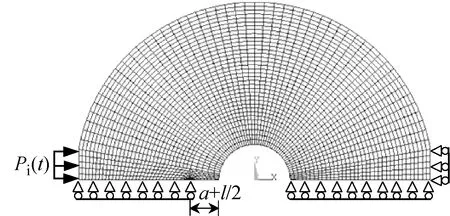
(b) HSCFBD裂纹扩展后的有限元模型

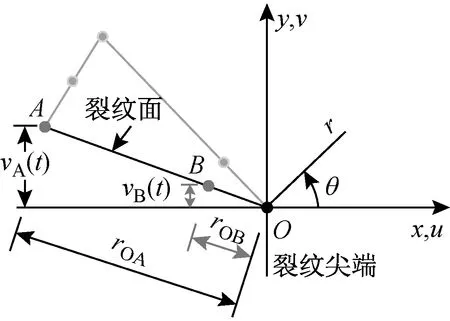
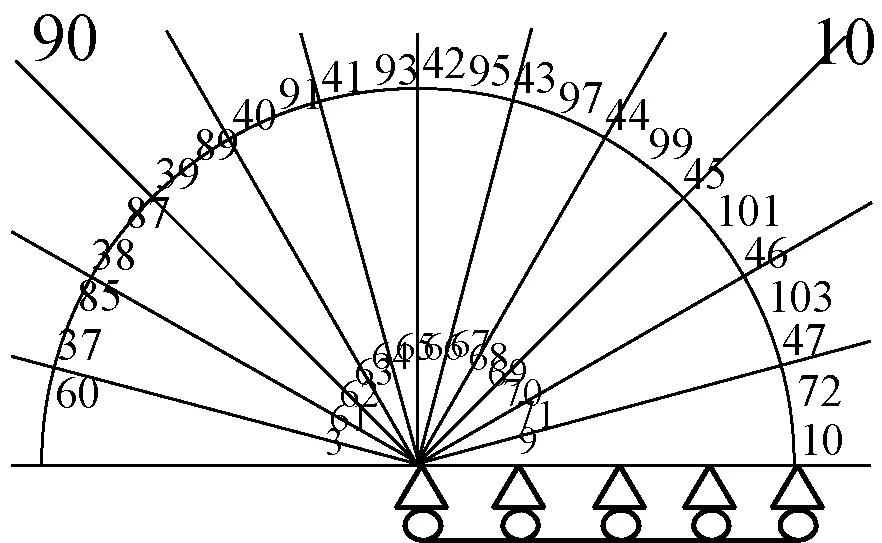
图12 裂尖极坐标系和1/4节点奇异单元Fig.12 Crack tip coordinate system and singular element with quarter points

(4)

式中：E，μ分别为材料的弹性模量和泊松比；r0B为奇异单元边长r0A的1/4；vA(t)为图12中A节点y方向位移的时间历程；vB(t)为图12中B节点y方向位移的时间历程。

3 普适函数对扩展裂纹动态应力强度因子的近似解析修正

普适函数体现了裂纹扩展速度在不超过Rayleigh波速时对动态应力强度因子的影响，即：在任何情况下，张开裂纹在一般荷载作用下以任意速度v扩展的动态应力强度因子等于瞬时裂尖的普适函数值乘上适用于具有该处静止裂纹在相同动荷载荷载下的动态应力强度因子，即：

(5)

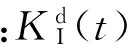
(6)

式中：cd是材料膨胀波波速；cR是材料Rayleigh波速。当裂纹不扩展即v=0时，k(0)=1；当裂纹扩展速度v=cR时，k(cR)=0，裂速在0～cR范围内k(v)单调递减。

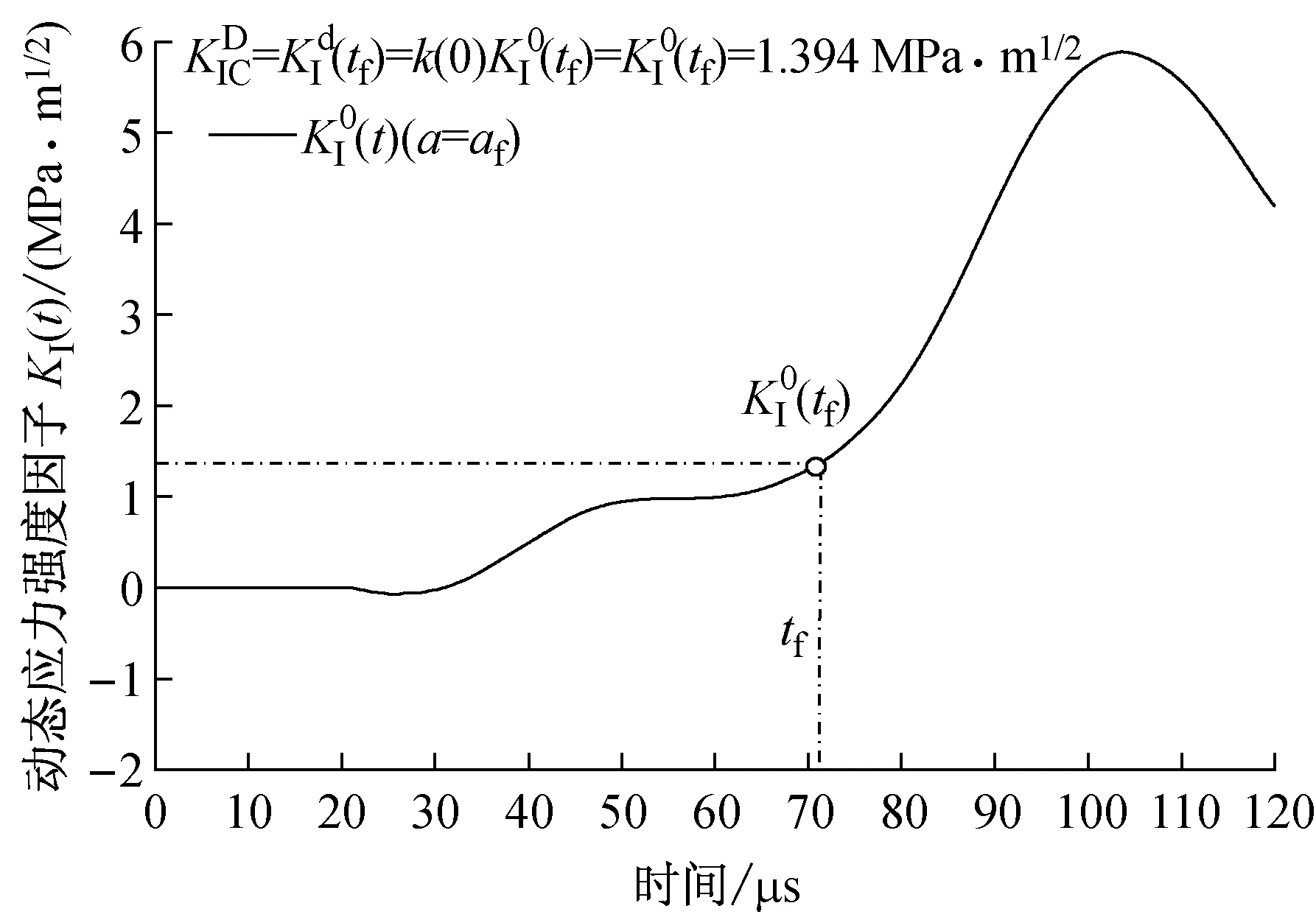
图13 HSCFBD-06试样动态起裂韧度的确定Fig.13 Determination for dynamic initiation toughness of HSCFBD-06 specimen

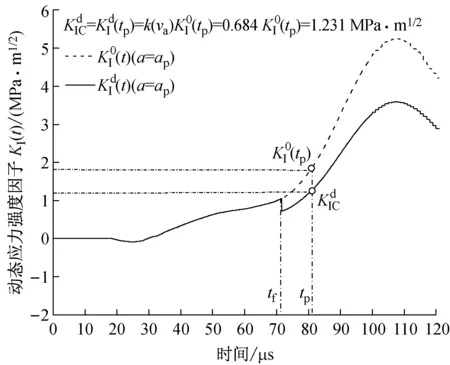
图14 HSCFBD-06试样动态扩展韧度的确定Fig.14 Determination for dynamic propagation toughness of HSCFBD-06 specimen

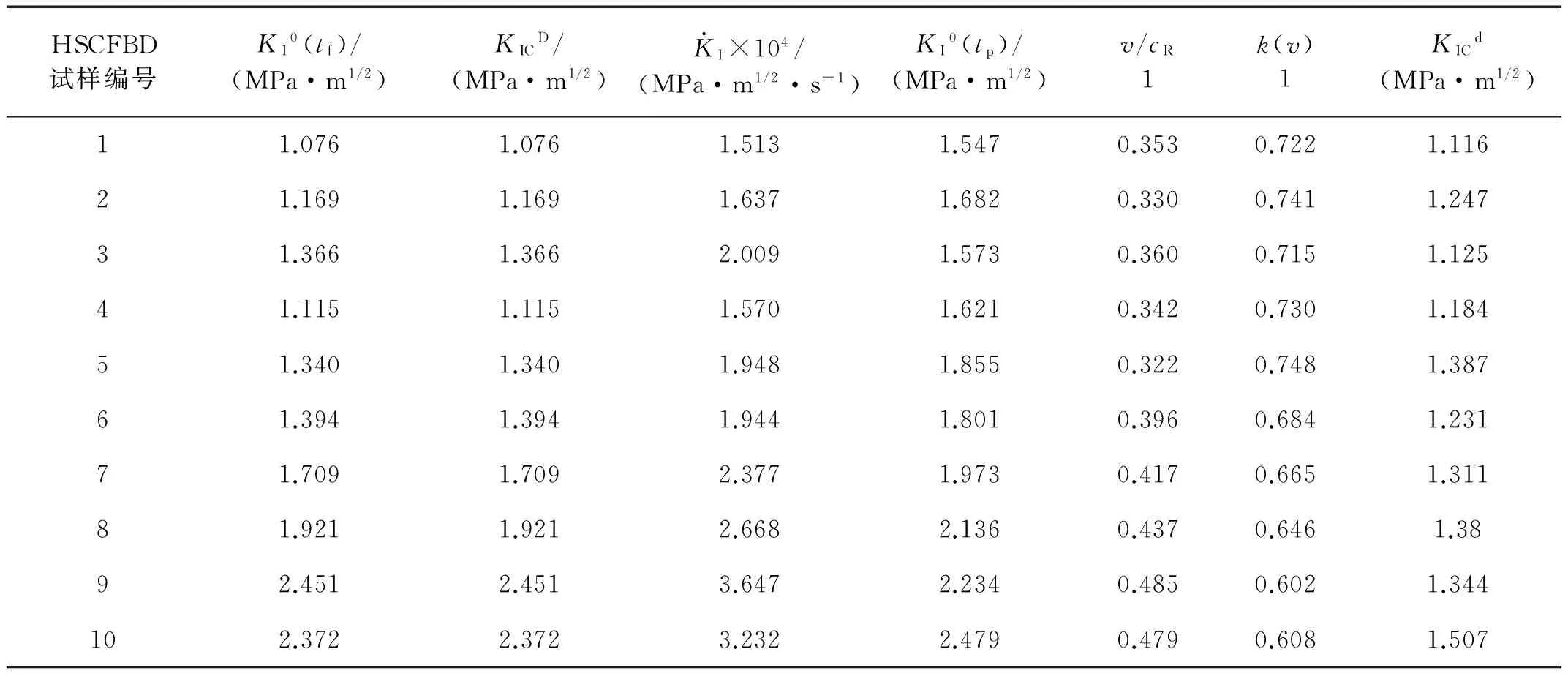
表2 用实验-数值-解析法所得动态断裂韧度(KICD、KICd)Tab.2 Dynamic fracture toughness(KICD、KICd) obtained by experimental-numerical method

(7)

(8)

动态实验10个HSCFBD试样的几何尺寸和预制裂纹均相同，则可根据动态起裂准则式(9)和动态扩展准则式(10)分别得到材料的动态起裂韧度和动态扩展韧度，如图13和图14所示。

(9)

(10)

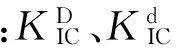
利用实验-数值-解析法得到砂岩的动态断裂韧度计算结果如表2所示。

4 测试结果分析与讨论

4.1 加载率和裂速对动态断裂韧度的影响

隆昌青砂岩动态起裂韧度与动态加载率之间的关系如图15所示，本次实验的动态加载率范围为(1.513～3.647)×104MPa·m1/2·s-1，在此范围内，砂岩的动态起裂韧度随着加载率的提高呈上升趋势。将本次实验结果与杨井瑞等[42]、张财贵等[44]和WANG等[45]的研究成果进行了对比。文献[42，44]与本文取材自同一批砂岩，文献[44]和本文试样同为圆环试样，所得结果比较吻合，文献[42]动态加载率较高，与本文结果接近于线性增长。从图15可以看出，砂岩在高加载率下对断裂的抵抗能力要比静态或低加载率的抵抗能力都要高。从微观来看，在静态或低加载率情况下，裂纹会选择最容易的方式扩展，多为沿晶破坏，而高加载率情况下，多为穿晶破坏，穿晶断裂比沿晶断裂消耗的能量要多得多[46]。从能量角度来看，高加载率下，比起裂纹起裂需要储存更大的能量用于裂纹高速扩展。

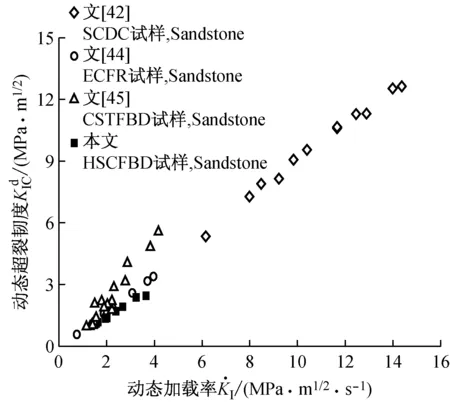
图15 动态起裂韧度与动态加载率之间的关系Fig.15 Relation between dynamic initiation toughness and dynamic loading rate

隆昌青砂岩动态扩展韧度与裂纹扩展速度的关系如图16所示，本次实验的裂纹扩展速度范围为(0.322～0.485)cR。在此范围内，砂岩的动态扩展韧度随裂纹扩展速度的提高而增加。当裂纹扩展速度在(0.322～0.353)cR范围内时，裂纹扩展速度有一定程度的上下动荡，这种现象主要和岩石本身的不均匀性以及裂纹高速扩展时更容易产生曲折的裂纹扩展路径有关。而当裂纹扩展速度在(0.353～0.485)cR范围内时，动态扩展韧度随裂速提高而增加。

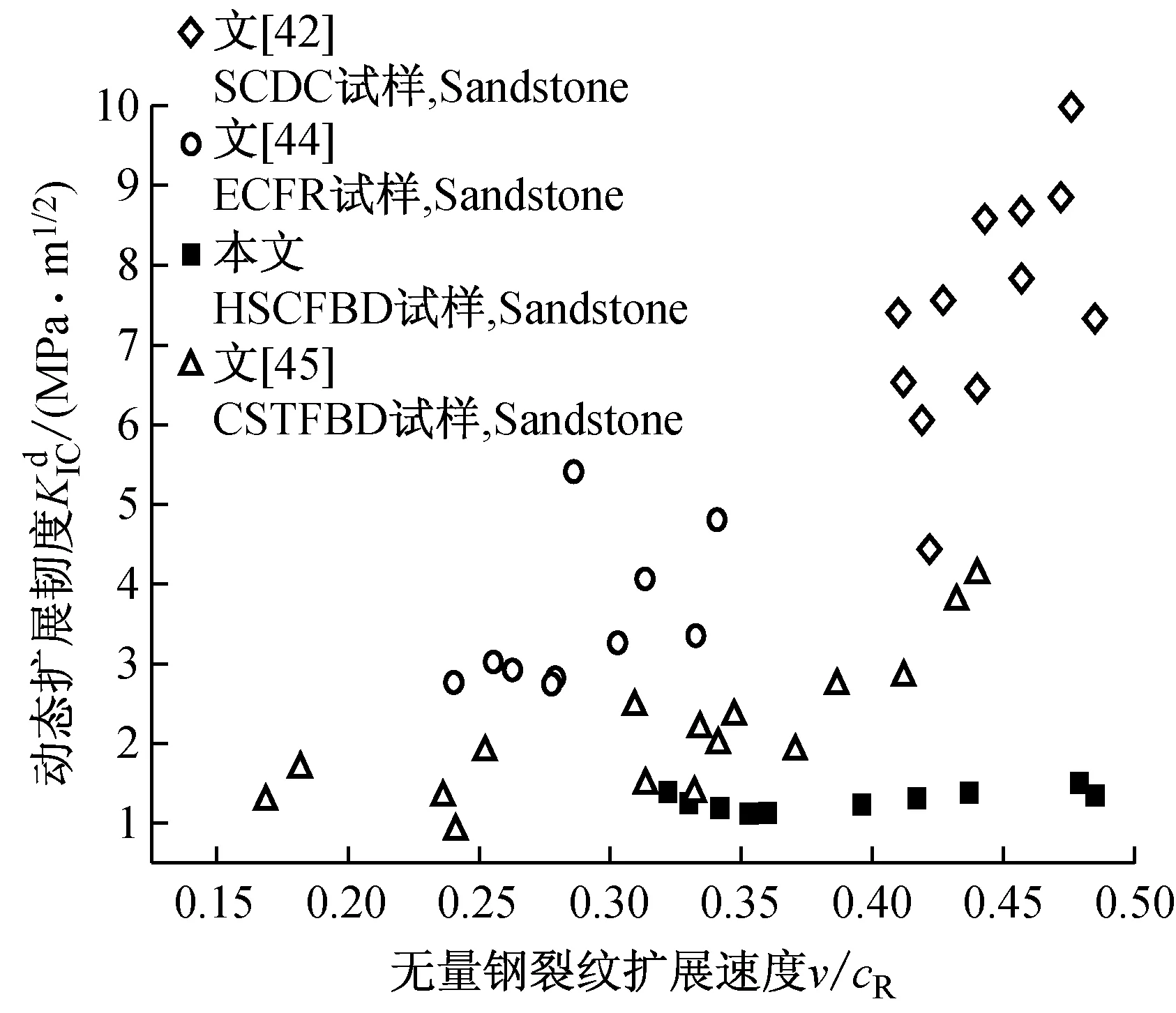
图16 动态扩展韧度与裂纹扩展速度之间的关系Fig.16 Relation between dynamic propagation toughness and crack velocity

4.2 关于HSCFBD实现裂纹止裂的讨论

要实现止裂，主要可以通过两方面。一是改变材料，选择断裂韧度更高的材料；二是减小试样的动态应力强度因子，可以通过降低动态荷载和改变试样尺寸参数的方式。从HSCFBD的静态数值标定结果可以看出应力强度因子随着裂纹的增长呈下降趋势。试样随加载率增长的趋势也比较明显。在不改变材料的前提下，通过选择合适的尺寸和实验时降低加载气压，可以采用HSCFBD试样对动态止裂韧度进行研究。

5 结 论

(1)用圆孔内单边裂纹平台巴西圆盘(HSCFBD)试样和实验-数值-解析法得到了砂岩的动态起裂韧度和动态扩展韧度。动态起裂韧度随着加载率的提高而增加，动态扩展韧度随着裂纹扩展速度的提高而增加。砂岩在高加载率下对断裂的抵抗能力要比静态或低加载率的抵抗能力都要高。

(2) 通过对HSCFBD试样静态断裂和动态断裂研究成果的分析可知，如果选择合适的试样尺寸和加载气压，HSCFBD试样可以用来进行止裂试验从而获得动态止裂韧度。

(3)在常用的动态断裂测试方法中，光学测试方法需要运用高速摄影，价格昂贵。岩石类材料所需大尺寸试样在动荷载作用下不易到达应力平衡，应用准静态方法测试动态断裂韧度并不合适。应变片法的实验条件也难以满足。相对而言，实验-数值-解析法是测试岩石动态断裂韧度是比较简单有效的方法。

[1] BAZANT Z P, CANER F C.Comminution of solids caused by kinetic energy of high shear strain rate, with implications for impact, shock, and shale fracturing[J].Proceedings of National Academy of Science, 2013, 110(48): 19291-19294.

[2] MOTT N F.Fracture of metals: theorertal consideration[J].Engineering, 1948, 165: 16-18.

[3] 范天佑.断裂动力学原理与应用[M].2版.北京：北京理工大学出版社，2006.38-43, 108-130.

[4] 周妍，张财贵，杨井瑞，等.圆孔内单边(或双边)裂纹平台巴西圆盘应力强度因子的全面标定[J].应用数学和力学, 2015, 36(1): 16-30.

ZHOU Yan, ZHANG Caigui, YANG Jingrui, et al.Comprehensive calibration of stress intensity factor for flattened Brazilian disc with holed inner single or double cracks[J].Applied Mathematics and Mechanics, 2015, 36(1): 16-30.

[5] ISRM Testing Commission, (co-ordinator: Ochterlony F), Suggested methods for determining the fracture toughness of rock[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1988, 25: 71-96.

[6] ISRM Testing Commission, (co-ordinator: Fowell R J), Suggested method for determining mode I fracture toughness using cracked chevron notched Brazilian disc (CCNBD) specimens[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1995, 32: 57-64.

[7] KURUPPU M D, OBARA Y, AYATOLLAHI M R, et al.ISRM-Suggested method for determining the mode I static fracture toughness using semi-circular bend specimen[J].Rock Mechanics Rock Engineering, 2014, 47: 267-274.

[8] ZHANG Q B, ZHAO J.A review of dynamic experimental techniques and mechanical behaviour of rock materials[J].Rock Mechanics and Rock Engineering, 2014, 47(4): 1411-1478.

[9] ISRM Testing Commission.Suggested method for determining tensile strength of rock materials[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1978, 15(3): 99-103.

[10] WANG Q Z, XING L.Determination of fracture roughness KICby using the flattened Brazilian disk specimen for rocks[J].Engineering Fracture Mechanics, 1999, 64: 193-201.

[11] RIPPERGER E, DAVIS N.Critical stresses in a circular ring[J].Trans Am.Soc.Civil Eng., 1947, 112: 619-27.

[12] HOBBS D W.The tensile strength of rocks[J].International Journal of Rock Machanics and Mining Sciences& Geomechanics Abstracts, 1964, 6(1): 91-97.

[13] 张盛, 王启智.用5种圆盘试样的劈裂试验确定岩石断裂韧度[J].岩土力学, 2009, 30(1):12-18.

ZHANG Sheng, WANG Qizhi.Determination of rock fracture toughness by split test using five types of disc specimens[J].Rock and Soil Mechanics, 2009, 30(1): 12-18.

[14] 张盛，王启智.采用中心圆孔裂缝平台圆盘确定岩石的动态断裂韧度[J].岩土工程学报, 2006, 28(6): 723-728.

ZHANG Sheng, WANG Qizhi.Method for determination of dynamic fracture toughness of rock using holed-cracked flattened disc specimen[J].Chinese Journal of Geotechnical Engineering, 2006, 28(6): 723-728.

[15] YOFFE E H.Moving Griffith crack[J].Philosophical Magazine, 1950, 42: 739-750.

[16] CRAGGS J W.On the propgation of a crack in an elastic-brittle material[J].J.Mech.Phys.Solids, 1960, 8: 66-75.

[17] BROBERG K B.The propgation of a brittle crack[J].Arkiv for Fysik, 1960, 18: 159-192.

[18] BAKER B R.Dynamics stresse created by a moving crack[J].Journal of Applied Mechanics, 1962, 29: 449-458.

[19] DALLY J W, FOURNEY W J, IRWUN G R.On the uniqueness of the stress intensity factor-crack velocity relationship[J].International Journal of Fracture, 1985, 27(3/4): 277-298.

[20] 宋义敏，杨小彬，金璐，等.冲击荷载作用下岩石Ⅰ型裂纹动态断裂试验研究[J].振动与冲击, 2014, 33(11): 49-60.

SONG Yimin, YANG Xiaobin, JIN Lu, et al.Dynamic fracture test for rock I-type crack under impact load[J].Journal of Vibration and Shock, 2014, 33(11): 49-60.

[21] JOUDON V, PORTEMONT G, LAURO F, et al.Experimental procedure to characterize the mode I dynamic fracture toughness of advanced epoxy resins[J].Engineering Fracture Mechanics, 2014, 126: 166-177.

[22] DAI F, XIA K, ZHENG H, et al.Determination of dynamic rock mode-I fracture parameters using cracked chevron notched semi-circular bend specimen[J].Engineering Fracture Mechanics, 2011, 78(15): 2633-2644.

[23] ZHANG Q B, ZHAO J.Effect of loading rate on fracture toughness and failure micromechanisms in marble[J].Engineering Fracture Mechanics, 2013, 102: 288-309.

[24] GAO G, HUANG S, XIA K, et al.Application of digital image correlation (DIC) in dynamic notched semi-circular bend (NSCB) tests[J].Experimental Mechanics, 2014, DOI: 10.1007/s11340-014-9863-5.

[25] 苟小平，杨井瑞，王启智.基于P-CCNBD试样的岩石动态断裂韧度测试方法[J].岩土力学, 2013, 34(9)：2449-2459

GOU Xiaoping, YANG Jingrui, WANG Qizhi.Test method for determining rock dynamic fracture toughness using P-CCNBD specimens[J].Rock and Soil Mechanics, 2013,34(9): 2449-2459.

[26] WANG Q Z, FENG F, NI M, et al.Measurement of mode I and mode II rock dynamic fracture toughness with cracked straight through flattened Brazilian disc impacted by split Hopkinson pressure bar[J].Engineering Fracture Mechanics, 2011, 78(12): 2455-2469.

[27] 杨井瑞，张财贵，周妍，等.用CSTBD试样确定砂岩的动态起裂和动态扩展韧度[J].爆炸与冲击, 2014, 34(3): 264-271.

YANG Jingrui, ZHANG Caigui, ZHOU Yan, et al.Determination of dynamic initiation toughness and dynamic propagation toughness of sandstone using CSTBD specimens[J].Explosion and Shock Waves, 2014, 34(3): 264-271.

[28] 张财贵, 周妍, 杨井瑞，等.用边裂纹平台圆环(ECFR)试样测试岩石的Ⅰ型动态断裂韧度[J].水利学报, 2014, 45(6): 78-87.

ZHANG Caigui, ZHOU Yan, YANG Jingrui, et al.Determination of model I dynamic fracture toughness of rock using edge cracked flattened ring specimen[J].Journal of Hydraulic Engineering, 2014, 45(6): 78-87.

[29] POPELAR C H, ANDERSON C E, NAGY A.An experimental method for determining dynamic fracture toughness[J].Experimental Mechanics, 2000, 40 (4): 401-407.

[30] FREUND L B.Dynamic fracture mechanics[J].Cambridge University Press, Cambridge, 1990: 296-432.

[31] BHAT H S, ROSAKIS A J, SAMMIS C G.A micromechanics based constitutive model for brittle failure at high strain rate[J].ASME, Journal of Applied Mechanics, 2012, 79: 031016-1-12.

[32] REN X D, LI J.Dynamic fracture in irregularly structured systems[J].Physical Review E, 2012, 85: 055102-1-4.

[33] MARKUS J B, GAO H J.Dynamical fracture instabilities due to local hyperelasticity at crack tips[J].Nature, 2006, 439 (19): 307-310.

[34] 谢和平，高峰，周宏伟，等.岩石断裂和破碎的分形研究[J].防灾减灾工程学报, 2003, 23(4): 1-9.

XIE Heping, GAO Feng, ZHOU Hongwei, et al.Fractal fracture and fragmentation in rocks[J].Journal of Disaster Prevention and Mitigation Engineering, 2003, 23(4): 1-9.

[35] 卢芳云，陈荣，林玉亮，等.霍普金森杆实验技术[M].北京：科学出版社, 2013: 1-2.

[36] POPELAR C H, ANDERSON C E, NAGY A.An experimental method for determining dynamic fracture toughness[J].Experimental Mechanics, 2000, 40 (4): 401-407.

[37] 倪敏，苟小平，王启智.霍普金森杆冲击压缩单裂纹圆孔板的岩石动态断裂韧度试验方法[J].工程力学, 2013, 30(1): 365-372.

NI Min, GOU Xiaoping, WANG Qizhi.Test method for rock dynamic fracture toughness using single cleavage drilled compression specimen impacted by split Hopkinson pressure bar[J].Engineering Mechanics, 2013, 30(1): 365-372.

[38] 刘德顺，彭佑多，李夕兵.冲击活塞的动态反演设计与试验研究[J].机械工程学报，1998, 34(4): 78-84.

LIU Deshun, PENG Youduo, LI Xibing.Inverse design and experimental study of impact piston[J].Journal of Mechanical Engineering, 1998, 34(4): 78-84.

[39] LOK T S, LI X B, LIU D, et al.Testing and reponse of large diameter btittle materials subjected to high strain rate[J].Journal of Materials in Civil Engineering, 2002, 14(3): 262-269.

[40] 王晓燕，卢芳云，林玉亮.SHPB实验中端面摩擦效应研究[J].爆炸与冲击，2006, 26(2): 134-139.

WANG Xiaoyan, LU Fangyun, LIN Yuliang.Study on interfacial friction effect in the SHPB tests[J].Explosion and Shock Waves, 2006, 26(2): 134-139.

[41] 刘德顺, 李夕兵.冲击机械系统动力学[M].北京: 科学出版社, 1999.

[42] 杨井瑞, 张财贵, 周妍，等.用SCDC试样测试岩石动态断裂韧度的新方法[J].岩石力学与工程学报，2015, 34(2): 279-292.

YANG Jingrui, ZHANG Caigui, ZHOU Yan.et al.A new method for determining dynamic fracture toughness of rock using SCDC specimens[J].Journal of Rock Mechanics and Engineering, 2015, 34(2): 279-292.

[43] CHEN Y M, WILKINS M L.Numerical analysis of dynamic crack problem[J].Engineering Fracture Mechanics, 1975, 7: 635-660.

[44] 张财贵, 周妍, 杨井瑞，等.用分离式霍普金森压杆径向冲击边裂纹平台圆环(ECFR)试样的动态断裂试验[J].煤炭学报, 2015, 40(5): 1037-1046.

ZHANG Caigui, ZHOU Yan, YANG Jingrui, et al.Dynamic fracture test of edge cracked flattened ring (ECFR) diametrically impacted with split Hopkinson pressure bar[J].Journal of China Coal Society, 2015, 40(5): 1037-1046.

[45] WANG Q Z, YANG J R, ZHANG C G, et al.Sequential determination of dynamic initiation and propagation toughness of rock using experimental-numerical-analytical method[J].Engineering Fracture Mechanics, 2015：141：78-94.

[46] 谢和平, 陈至达.分形(fractal)几何与岩石断裂[J].力学学报, 1988, 20(3): 264-271.

XIE Heping, CHEN Zhida.Fractal geometry and fracture of rock[J].Chinese Journal of Theoretical and Applied Mechanics, 1988, 20(3): 264-271.

Determination of dynamic initiation toughness and dynamic propagation toughness of sandstone

ZHOU Yan1,2, ZHANG Caigui1, WANG Qizhi1,3

(1.Department of Civil Engineering and Applied Mechanics, University of Sichuan, Chengdu 610065, China; 2.School of Architectural Engineering and Art Design, Hunan Institute of Technology, Hengyang 421000;3.State Key Laboratory of Hydraulics and Mountain River Engineering, Chengdu 610065, China)

The opening-mode dynamic fracture test was conducted with sandstone specimens of holed single cracked flattened Brazilian disc, they were impacted with a large-diameter (∅100 mm) split Hopkinson pressure bar.Considering influences of material inertia effect and crack propagation velocity on the dynamic stress intensity factor, an experiment-numerical-analytical method was used to obtain the dynamic initiation toughness of sandstone under different dynamic loading rates, and the dynamic propagation toughness of sandstone at different crack propagating velocities.Firstly, dynamic loading histories of specimens were obtained in dynamic tests.The crack initiation instant and crack propagating velocity of a specimen were sequentially measured with a crack propagation gauge (CPG).The universal function value corresponding to the crack propagating velocity was obtained.Then, the dynamic numerical simulation was conducted using a finite element software and taking the dynamic loading histories as inputs to obtain the dynamic stress intensity factor histories of a static crack, they were modified with the corresponding universal function value.Finally, according to the crack initiation instant and the instant crossing the middle point of the CPG, the dynamic initiation toughness and the dynamic propagation toughness were determined with the corresponding histories of the dynamic stress intensity factor.It was shown that the dynamic initiation toughness of sandstone increases with increase in dynamic loading rate, and the dynamic propagation toughness of sandstone increases with increase in crack propagation speed.

holed single cracked flattened Brazilian disc; experimental-numerical-analytical method; dynamic initiation toughness; dynamic propagation toughness; crack propagation gauge; universal function

高等学校博士学科点专项科研基金(20130181130013)

2015-06-19 修改稿收到日期：2016-01-25

周妍 女，硕士，1989年8月生

王启智 男，教授，博士生导师，qzwang2004@163.com

O347.3；TU458

A

10.13465/j.cnki.jvs.2017.05.007