施加水平磁场下电磁声发射与裂纹指向特征分析
2017-04-10蔡智超刘素贞张严伟杨庆新
蔡智超,刘素贞,张 闯,张严伟,杨庆新,3
(1.华东交通大学 电气与自动化工程学院,南昌 330013;2.河北工业大学 电磁场与电器可靠性省部共建重点实验室,天津 300130;3.天津工业大学 电工电能新技术天津市重点实验室,天津 300387)
施加水平磁场下电磁声发射与裂纹指向特征分析
蔡智超1,刘素贞2,张 闯2,张严伟2,杨庆新2,3
(1.华东交通大学 电气与自动化工程学院,南昌 330013;2.河北工业大学 电磁场与电器可靠性省部共建重点实验室,天津 300130;3.天津工业大学 电工电能新技术天津市重点实验室,天津 300387)
声发射检测方法对金属构件进行健康检测的关键问题:通过合适的载荷使得构件产生声发射信号。现阶段大部分声发射检测均采用接触式离线加载,声发射检测采用可在线检测的非接触式电磁加载。从电致位错、自由电子运动理论出发,在微观层面探究电磁声发射的机理特征;研究静磁场与涡流分布作用下电磁声发射特征差异;基于声发射信号的非平稳特征,利用希尔伯特黄变换方法分析电磁声发射特征。通过改变水平磁场激励方向,实现本征模态函数的能量比值、互相关系数、特征本征模态函数时频图与裂纹指向特征之间的关系联立。
电磁声发射;水平磁场;希尔伯特黄变换;裂纹指向性
目前,声发射作为一种动态无损检测方式对金属构件的在线监测、活性缺陷区域适时判断已在工程应用上取得了广阔的进步。并在声波传感技术、远距离信号采集等硬件设备的研制、材料声发射特性及非平稳大数据量信号处理、桥梁叶片等大型工程结构的健康应用诊断、新型声发射技术的实验研究等诸多方面深入发展并彰显良好的应用前景[1]。
电磁声发射检测技术通过在金属材料中的缺陷处引入电磁激励并释放能够反映缺陷信息的一定能量的瞬态应力波[2-4],所引入电磁加载的方式常见有接触式直接大电流加载、非接触式涡流加载,其目的是为了能够在缺陷尖端处产生电流集中进而将产生更为强的电磁式加载效应。并实现在板状金属构件与管状金属构件中裂纹检测的可行性,该技术兼顾声发射对动态裂纹检测效率以及电磁无损检测的非接触、无需耦合剂、恶劣环境下局部加载等独特优势[4-5]。
然而电磁声发射理论及机理研究仍不够系统:电磁加载过程中电场和磁场两者如何联立作用并产生声发射信号,电磁声发射信号与普通电磁加载弹性波有何本质区别,如何利用电磁声发射固有特点探究裂纹深层次特性,这依然是制约其工程应用的瓶颈。本文搭建基于位错动力学的电磁声发射模型,阐述电磁载荷下漂移电子的定向流动与位错之间能量转换是产生电磁声发射的主要原因。
考虑到致使工程构件失效重要原因众多,其中包括动态特征——“裂纹的指向特性”。如对其能有效的检测可实现在结构健康监测系统中对裂纹生长的定量损伤评估,因此对于裂纹指向特性检测也尤为显得重要。本文通过电磁声发射对裂纹指向性检测进行探索,利用希尔伯特黄变换方法应用于不同裂纹指向的电磁声发射信号特征提取与分析。结果表明水平磁场激励下电磁超声信号能够反映裂纹指向特征。
1 电场在电磁声发射过程中的效应分析
电流的引入是电磁声发射过程的先决条件,当给金属材料施加一定条件的强涡流激励,将对其流变应力、延伸率、应力松弛、蠕变、裂纹和疲劳产生一定的影响,并促使更多位错出现脱钉、运动及湮灭等现象。
2.1.1 电流加载特性
瞬时高密度电流作为一种附加能量的注入对原子的随机运动将产生影响,促进原子的扩散能力,推动位错的运动(滑移、攀移)。这与金属的变形机制有着密切的联系。
高密度电流不仅增强自由电子的运动,其高速运动还将促使自由电子与其他粒子不规则的碰撞并实现能量传递,产生位错增殖等现象,CONRAD等[5-6]将定向运动电子与不规则原子排列产生的位错作用情况定义为电子风力,并将该过程运用于解释电致塑性及电致成型加工技术并取得广泛认可:
σew=ξewJ
(1)
式中:σew为单位位错长度下的电子风力值;ξew为电子风力的系数,该系数是由材料的导电特性所决定的;J为引入的外加电流密度。式(1)表明电子风力与电流密度呈正比关系。
电流激励除了引入电子风力,实际上还包含多物理场问题:电磁、结构、温度之间能量会发生相互转化,该过程将会引入包括热效应在内的诸多附加作用。由于电磁声发射激励过程所通过的电流时间约为100 μm,因温度场引发的热压力远小于电子风力,因此可忽略该过程的附加效应,微观动应力将主要以电子风力为主。
一般情况下,材料的塑性应变率[6-7]可表示为
(2)

(3)
结合式(2)、式(3)可得:
(4)

(5)
2.1.2 声发射应力波释放
表征材料屈服特性的流变应力可以表示为[8]:
(6)
式中:K为强度系数;n为应变硬化指数,上述方程是由Fields-Backofen提出,适用于绝大部分金属材料。联立整体位错密度ρ与流变应力的关系式[9]:
σ=kmρ0.5
(7)
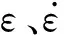
(8)
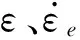
(9)
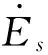
(10)
式中:产生声发射效应的应力σe以电子风力为主,在不同构件加载过程中σe会包含构件中的残余应力,考虑到电流加载的瞬时突发性,在涡流持续过程内近似假如将位错速度ve保持恒定。可动位错在金属声发射过程所释放的总能量为
对于螺旋位错:
(11)
对于刃型位错:
(12)
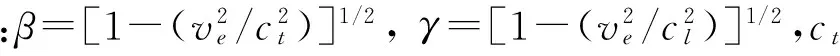
联立式(9),(11)与(12)可以看出,大量定向移动的自由电子运动克服位错间的势垒过程,释放一定的能量并伴随声发射应力波的产生。该过程主要受电流密度值的影响,随着电流密度值的增加,该过程效应逐渐增强。此外,电磁声发射产生还与电流路径与位错重叠情况以及趋肤深度等其他因素有关。
金属构件存在损伤时,裂纹尖端处位错密度显著,当电磁声发射换能器扫描至裂纹正上方时,流经尖端的涡流也将重新分配并呈现涡流集中效应。由于电磁声发射过程主要依赖于材料已有位错与作用的电磁激励,因此裂纹尖端比其他区域更易产生声发射效应。
2 磁场在电磁声发射过程中的效应分析
外加的电磁场总比晶体自身周期场弱得多,对于引入的磁场可在晶体中周期场的本征态基础上讨论。通常有两种方法进行分析:求解含有外加势场的波动方程;或把自由电子运动近似当作经典粒子来处理。由于电磁声发射过程中外加磁场为匀强磁场,可通过经典粒子动力学方式进行处理。
在电场载荷下自由电子移动过程将伴随着不停散射,所获得的场能及时地与所碰撞的原子进行交换,即在导体内受到电场力的作用,移动电子并不会加速运动。这与传统研究电子在真空环境下的运动规律是有区别的。导体中电场的存在仅为电子提供了一个定向稳定速度而非连续不断的电场力。若同时施加一个匀强磁场,可把问题简化描述为匀速带电粒子在匀强磁场中的运动情况,即金属材料霍尔效应:
(1) 当电子的初速度方向与磁感应线平行,那么电子受到的作用力为零,粒子做匀速直线运动。
(2) 当电子的初速度方向与磁感应线垂直,由于粒子受到的作用力与速度方向垂直,这也表明电场不影响电子运动速度的大小。均匀磁场与运动电子产生的洛伦兹力却时刻改变着电子运动的方向,电子将垂直于磁感应强度的平面上做匀速圆周运动。
(3) 当电子的初速度与磁场方向成任意角度,该速度可以分解为平行于磁场方向的速度径向分量及垂直于磁场方向的速度轴向分量,径向速度使电子作圆周运动,而轴向分量使电子平移,二者的综合作用是使电子按螺型轨迹前进。径向速度大的电子,其螺型轨道的直径变大,而径向速度小的电子,螺型直径变小。
预设含电荷为e、重量为me的漂移电子速度ve方向与磁场B方向间有θ夹角,粒子做螺型运动的半径Re为
(13)
自由电子所做螺型运动的螺间距hθ为
(14)
假定自由电子运动方向为X方向,图1所示:准垂直磁场方向的不同(大箭头方向表示,即在Z0X平面)将直接影响到自由电子螺型运动的半径及螺间距大小,运动轨迹将直接影响到自由电子与位错之间碰撞。图2表征水平磁场方向对自由电子运动的影响,值得注意的是水平磁场方向如在Y轴方向附近稍微偏转如图2(a)所示,漂移电子运动所产生的螺旋轨迹发生明显不同,由于所施加的水平磁场大小保持不变,从图2(b)~(e)中可看出电子螺旋运动的半径及螺间距保持一致。对比图2(b)、(c)所示,其切向速度方向保持不变,螺线轴向速度方向运动相反,对比图2(b)、(d)所示,其切向速度方向相反,螺线轴向速度方向保持不变,即水平磁场X轴分量影响电子螺线轴向运动,水平磁场Y轴分量影响电子切向运动。
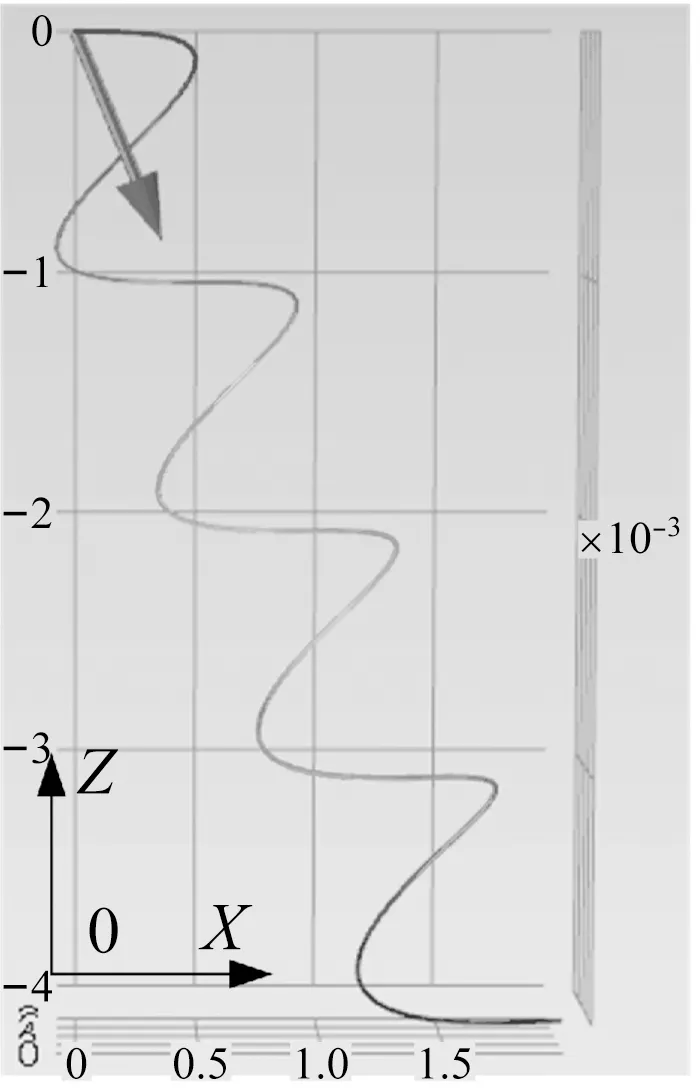
(a) θ=45°
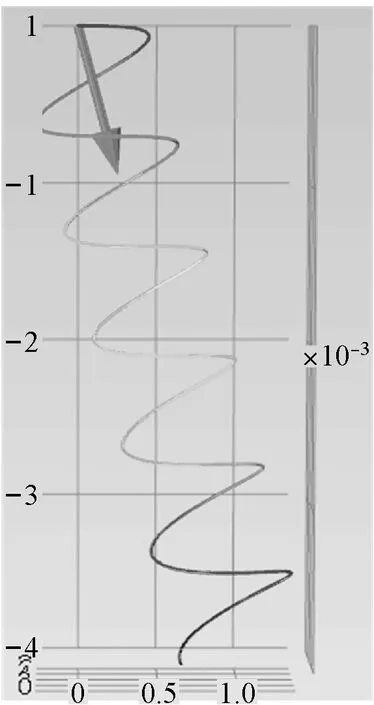
(b) θ=60°
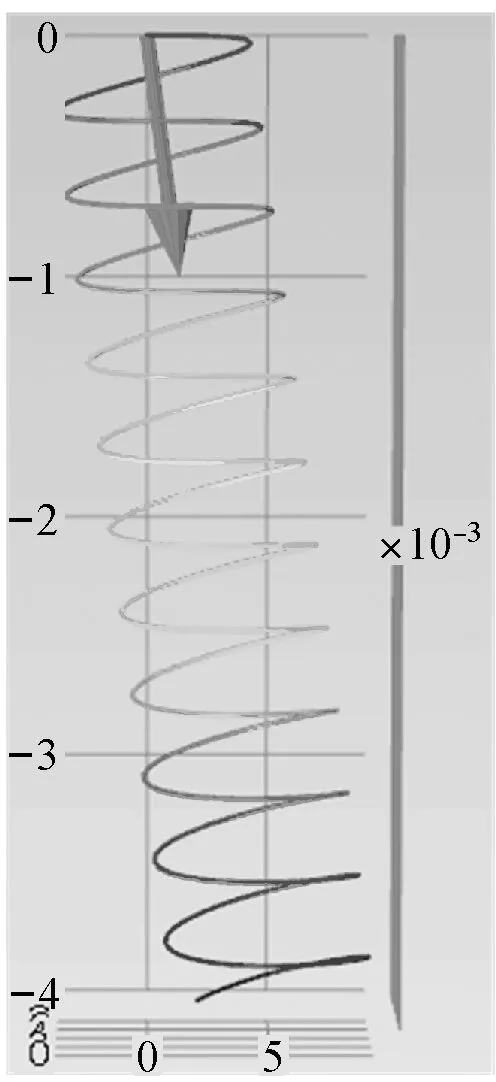
(c) θ=75°
Fig.1 The electron trajectories under different quasi-vertical directional magnetic field
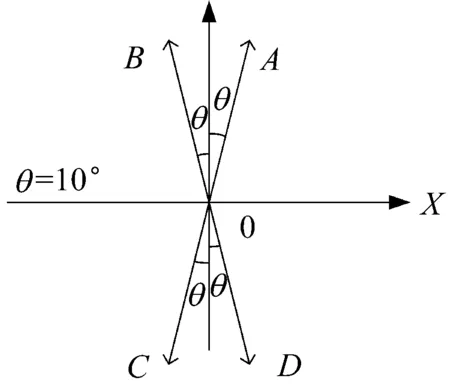
(a) 水平磁场方向示意图

(b) 水平磁场0A方向示意图
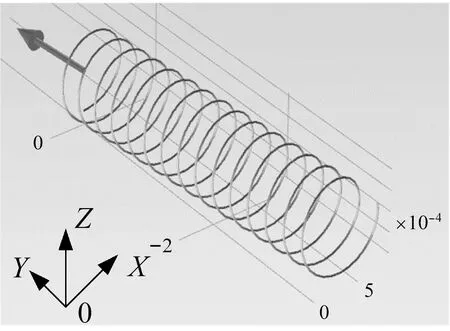
(c) 水平磁场0B方向示意图
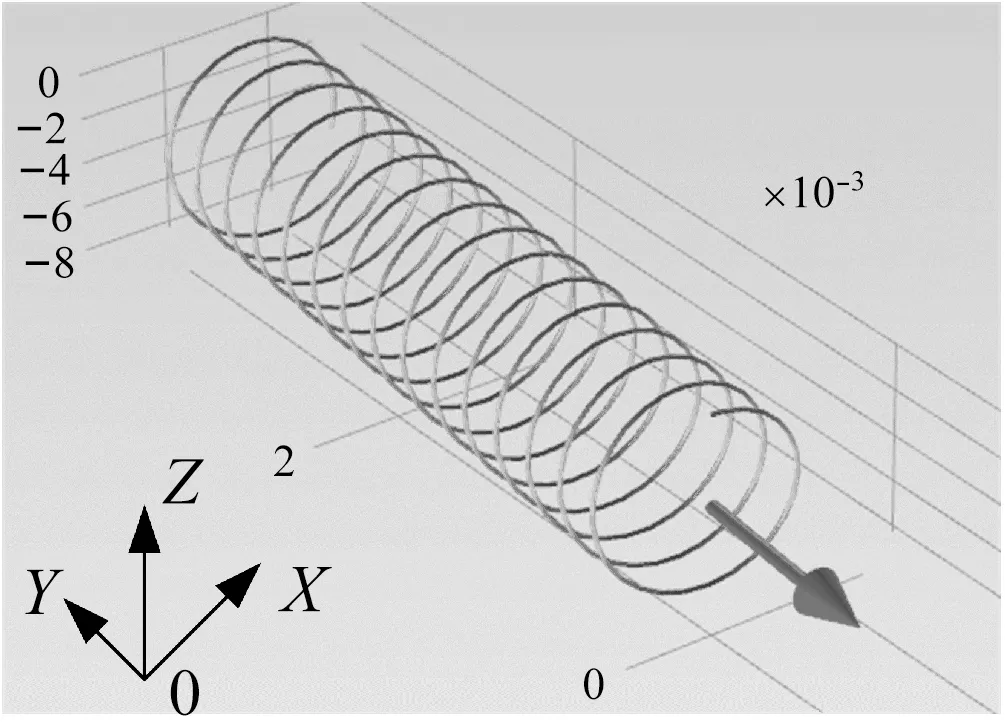
(d) 水平磁场0C方向示意图
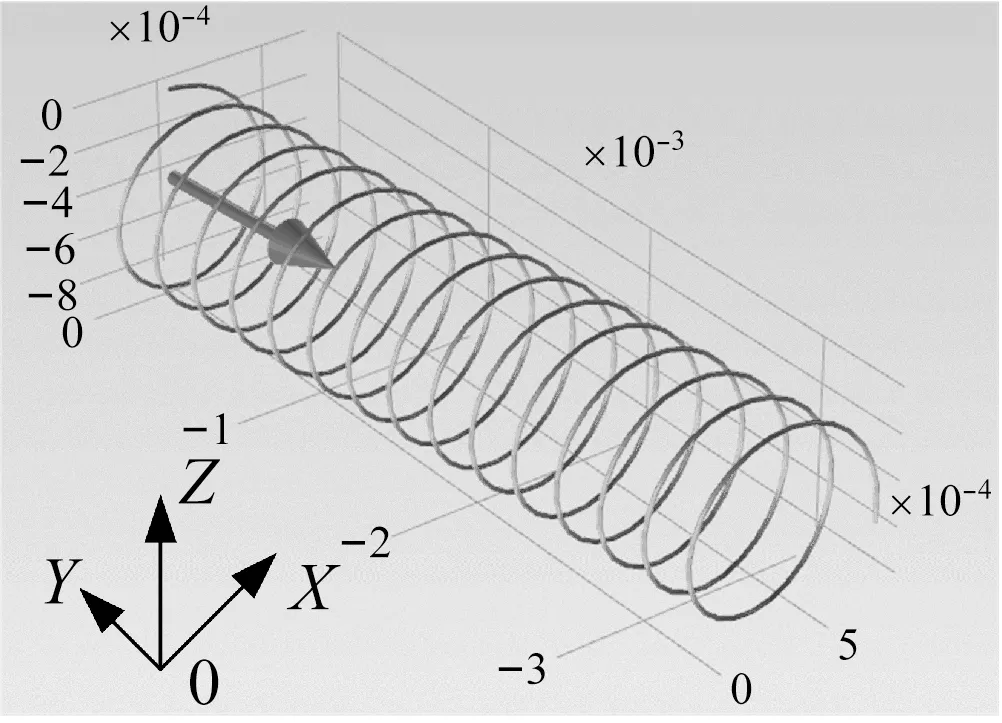
(e) 水平磁场0D方向示意图
Fig.2 The electron trajectories under different horizontal directional magnetic field
综上分析可知,施加平行于试件表面的水平磁场,可灵活控制漂移电子的径向运动、切向运动以及螺旋轴向运动。漂移电子运动范围覆盖了整个XOY平面,施加水平磁场相比施加准垂直磁场更易控制、操作。
3 水平磁场作用下电磁声发射实验研究
3.1 实验平台的搭建
电磁声发射实验平台如图3所示:美国Ritec5000提供的高频高功率激励作用于电磁声发射(EMAE)换能器,引入阻抗匹配实现较高功率的传输,当EMAE换能器扫描至裂纹尖端,高频涡流的趋肤效应、裂纹处电流集中效应使得裂纹尖端的涡流密度比其他区域上升多个数量级,与尖端数量显著的位错相互作用产生声发射应力波,接收端采用宽频WSA型(0~1 MHz)压电换能器,信号经过40 dB放大进入PCI-2声发射采集系统上位机显示、存储。
声发射信号采集系统设定模拟滤波器为0~600 kHz以消除过滤高频激励产生的电磁超声信号、采样率为5 MHz、阈值去噪门槛为45 dB。由于电磁声发射是自由电子推动金属构件中已有位错的结果,其传递出来为结构损伤信息,薄铝板电磁声发射信号频带为0~600 kHz。这有别于电磁超声换能过程中产生的弹性波信号,弹性波信号传递出来的为具有可重复性的电磁激励信息。电磁加载过程当中,不可避免将会产生弹性波,使用高频涡流(>600 kHz)加载方式及低通滤波器的配合使用,从频谱段实现对两种信号区分,因此激励信号使用频率为700 kHz、50 A的猝发式电流。
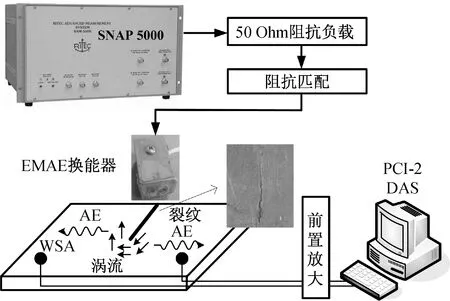
图3 电磁声发射实验过程Fig.3 The EMAE experiment system
3.2 水平磁场激励下电磁声发射实验
EMAE换能器由激励线圈与提供静磁场的永磁体组成,激励线圈采用圆形螺旋状并使用柔性印刷电路板制备,如图4所示。EMAE换能器在试件表面提供的涡流均匀分布且不易受裂纹指向性影响,永磁体采用高磁能积钕铁硼制备的马蹄形磁体,提供稳定水平方向高磁感应强度的静磁场,图中由N、S表示磁极,B指代水平磁场在平面上的静磁场磁感应线方向。本文针对6061铝合金(0.5 m×0.2 m×0.001 3 m)预制拉伸裂纹进行涡流加载电磁声发射实验。在实验过程中通过改变马蹄形与裂纹的相对位置,实现改变裂纹的相对指向。
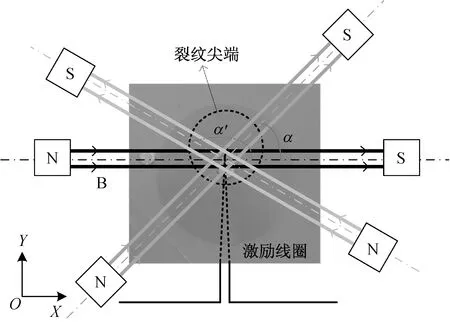
图4 EMAE换能器线圈示意图Fig.4 The diagram of EMAE transducer
以试件边界X方向为基准轴,α表示水平磁场方向与基准轴夹角:当α=0°表示水平磁场方向与裂纹指向夹角为90°,当α=90°时水平磁场方向与裂纹指向保持一致。α至α′表示马蹄形磁体旋转方向且分别表示起始角与终止角,本文夹角α=0°至α′=180°,在保证施加电流激励不变的情况下以30°为步长,实现水平磁场方向与基准夹角分别为0°、30°、60°、90°、120°、150°、180°,共七组特征夹角下电磁声发射实验。
4 实验结果分析
4.1 基于希尔伯特黄变换电磁声发射信号分析
电磁声发射信号为瞬态非线性、非平稳信号,而且电磁声发射信号特征的提取与时间分辨率关系密切,通过传统时频分析方法处理的频谱能量较宽(频谱能量易发生泄露)、时频分辨率粗糙,进而影响电磁声发射信号特征提取、分析的可信度。
与以傅里叶变换为基础的短时傅里叶变换(STFT)、小波变换(WT)、Wigner-Ville分布(WVD)等时频分析方法相比,希尔伯特黄(Hilbert-Huang, HHT)变换方法可对非线性、非平稳信号的局部时变特征进行自适应的时频分解并增强了时频集聚性,降低频谱能量泄露的同时提高了时频分辨率[12]。
HHT方法首先对原始信号进行经验模式分解(EMD),进而将信号表示成有限个本征模态函数(IMF)以及一个残余分量的形式,如图5所示。再利用Hilbert变换对上述分量进行时频分析和瞬时频率求解,如图6所示:声响应瞬时频率在时间轴上有较为显著离散。实为电子与低频段势垒碰撞的呈现出频率能谱分散等特征,同时也表明声发射并不具有弹性波(超声波)时频图中瞬时频率保持连续等特点。
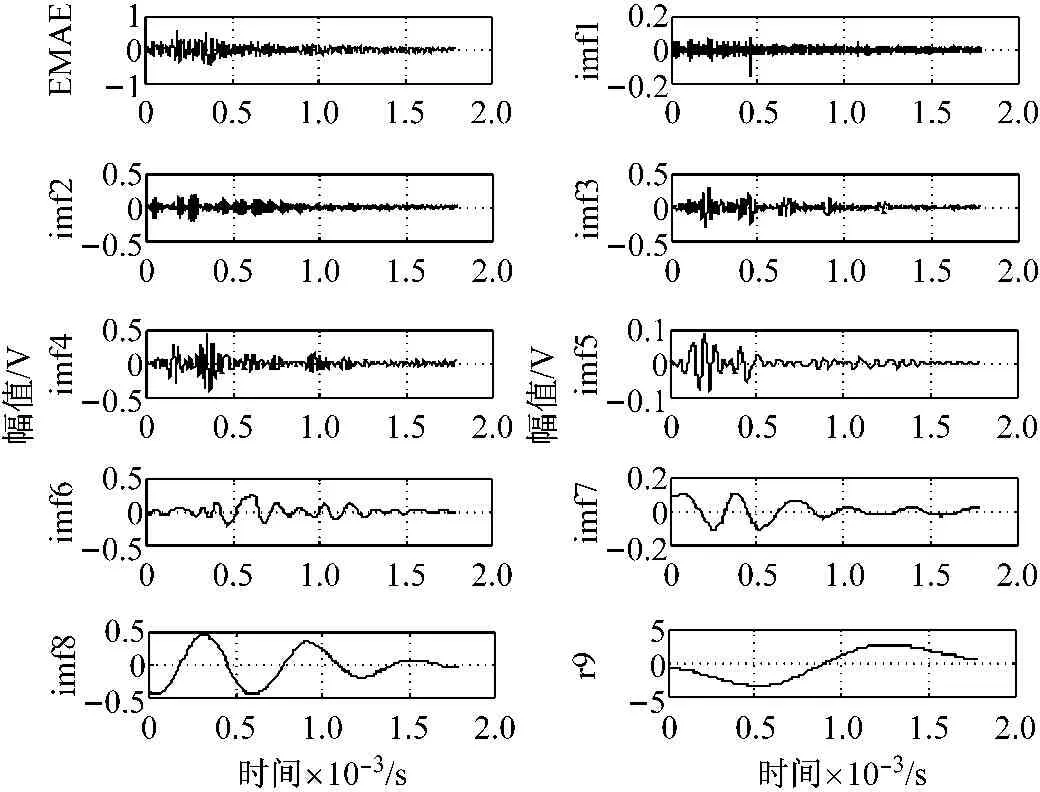
图5 电磁声发射原始波形及IMF时域图
Fig.5 Original EMAE waveform and IMF time domain diagram.
而后通过Hilbert谱图及Hilbert边际谱对声发射信号特征进一步分析,IMF分量较好地表现了信号的时频特性,电磁声发射信号频率主要集中于20 kHz与100 kHz两个峰值,如图7(a)所示。且低频信号持续的时间比高频信号持续更长、能量更强。
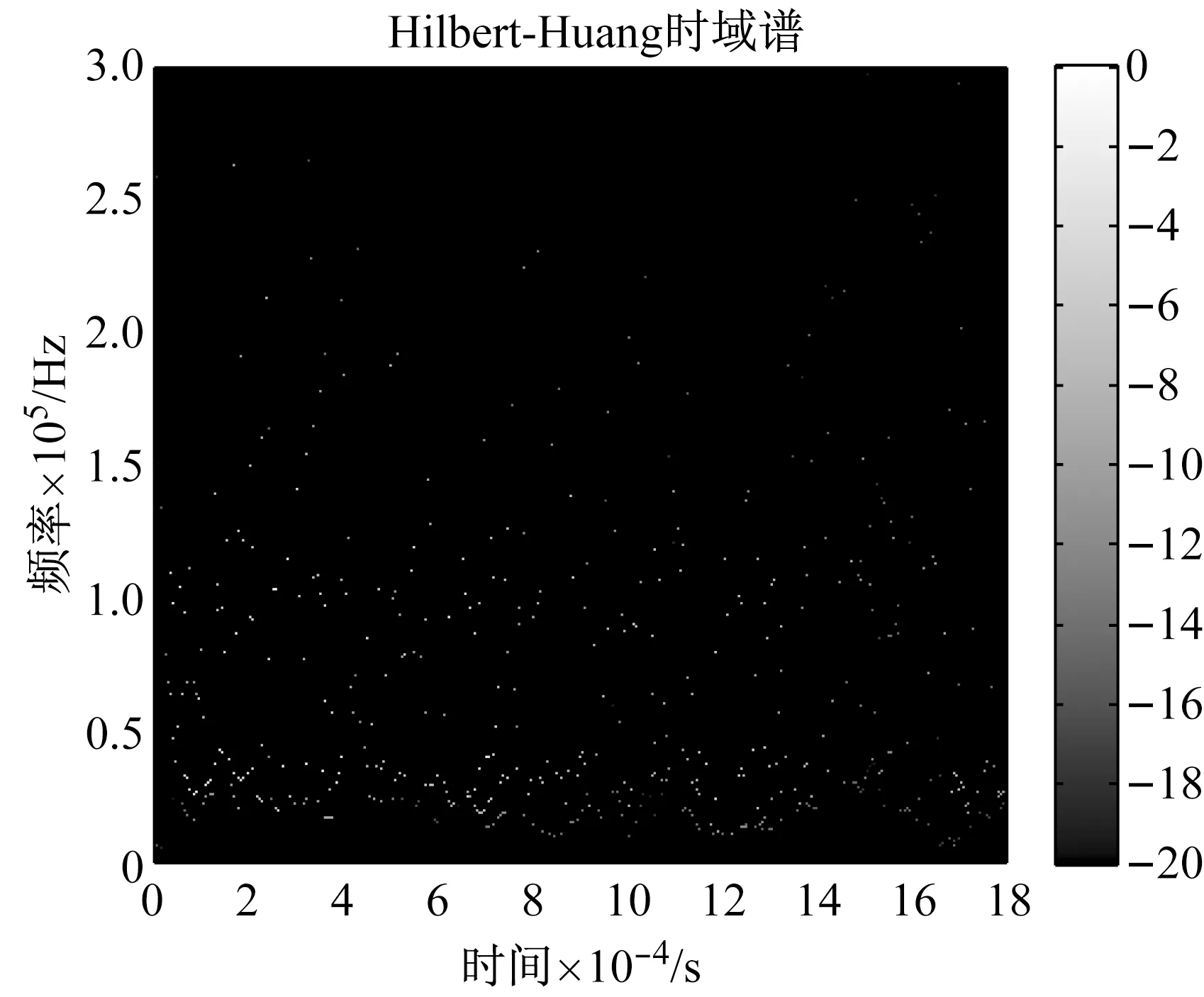
图6 电磁声发射信号希尔伯特黄变换谱图Fig.6 EMAE simulation signal analysis using HHT method.
图7中对比电磁声发射信号HHT变换计算后的边际谱与快速傅里叶变换计算的幅频图,两者具有相似的幅频特性,然而HHT变换可以显著突出边际谱的精确程度,并且在边际谱突出了各个IMF分量频率特性。这也验证了利用HHT变换比FFT变换更优的频率分辨效率。
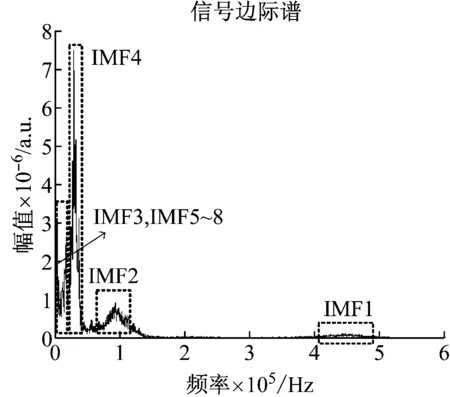
(a) 希尔伯特黄变换

(b) 快速傅里叶变换
4.1 水平磁场加载与裂纹指向特性关系分析
HHT由于结合了将时域信号按照频率尺度分解的EMD算法,所以其原始信号的非线性、非平稳等特点由不同特征的波动尺度分解至各个IMF分量,进而其所占的不同的平均能量,可由下式计算得出:
(15)
式中:n表示为电磁声发射信号的长度,该值是由采样长度与预触发值有关;ci(k)代表第i个IMF分量中的第k个元素;每个IMF分量的能量比值为
(16)
式中:Et表示IMF分量的总能量,即为各个Ei之和。进一步求解可得信号中95%以上的能量集中于1~5 IMF分量,所以对这五个分量深入分析,实验对比不同水平磁场角度下电磁声发射信号前5个IMF分量的能量比值,如图8所示。
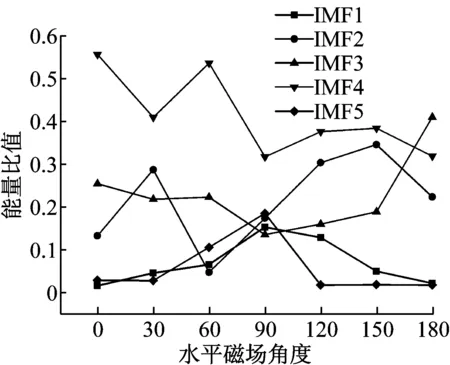
图8 IMF1~5分量的能量比值与水平磁场激励特性关系
Fig.8 The relationship between the energy percentage of IMF1~5 components and the exciting character of horizontal magnetic field.
由图8可知,IMF4包含40%以上的信号能量,IMF1与IMF5能量所占比重一直维持在5%~15%之间波动,且其在α=90°(水平磁场方向平行于裂纹指向)时能量比重占最大,而IMF3能量所占比重则在该点处最小,IMF1、IMF3、IMF5分别在α=0°~90°以及α=90°~180°成规律性变化。而IMF2与IMF4能量比值并无明显的规律,然而在90°两边变化趋势有所不同:在0~90°IMF2与IMF4变化趋势显著相反,而90°~180°IMF2与IMF4变化趋势明显相同,这也提供通过趋势变化特点来确定缺陷的指向与水平磁场角度的关系,同样在90°情况,IMF1~IMF5能量比值相对均匀,IMF1~IMF3、IMF5能量比值更为在16%~20%小范围之间尤为接近。
依据IMF分量能量比值,进一步对比分析各个IMF分量与电磁声发射原始信号的互相关系数,计算所得前五个分量与原始信号的互相关系数都在0.1以上,而余下的分量其相关性低于0.1,可以划分为没有相关性之列,通过上述分析可以发现,高互相关性的IMF分量相对占据高能量比值。因此选择前五个IMF分量进行对比分析,如图9所示。
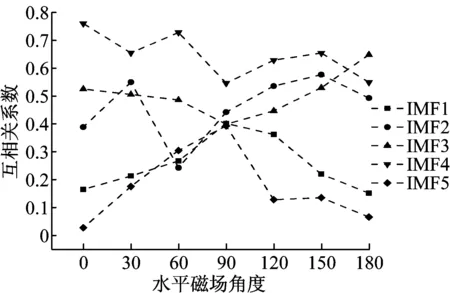
图9 IMF1~5分量的互相关系数与水平磁场激励特性关系
Fig.9 The relationship between the cross-correlation coefficient of IMF1~5 components and the exciting character of horizontal magnetic field.
联立图8与图9,说明能量比值与互相关性系数之间的正比对应关系,同时也相互应照了前五个IMF分量的表征原始信号的能力。
相比其他IMF分量,IMF5分量的能量比在α=90°条件下值达到了最高,且α=0~90°、α=0~180°条件下能量比值分别具有一定的单调关系;同时IMF5分量在整个实验周期内其互相关系数变化最为显著,这说明水平磁场角度的变化对低频段分量影响最为强烈。因此选用IMF5分量来进一步表征磁场与裂纹指向之间的关系,并对该分量进行希尔伯特黄变换,如图10所示。
由于涡流在裂纹尖端将会产生绕流,尖端处的电流将与裂纹指向保持垂直,当裂纹与水平磁场夹角为90°时,如图10(a)与(g)其IMF5分量集中于50 kHz~200 kHz,且其持续的时间一直贯穿于整个采集过程,这是由于该过程磁场加载方向与电场加载方向一致,即磁场不影响电子的定向流动,仅有电流效应作用于位错势垒,传递出来的信号特征相对稳定持续进而产生的声发射频率特征在小范围内波动。如图10(b)、(c)、(e)、(f)所示,伴随着磁场夹角发生改变,当水平磁场与裂纹指向一致时,其频谱波动情况最为明显IMF5分量集中于50 kHz~450 kHz,然而其持续时间以及瞬时频率却并不稳定,这说明磁场影响了电子的运动轨迹,电流及磁场共同作用于位错势垒,进而其频谱范围发生了扩展,流动的漂移电子促使结构内位错运动撞击发生改变,反馈出包含裂纹指向特性的声发射信号。
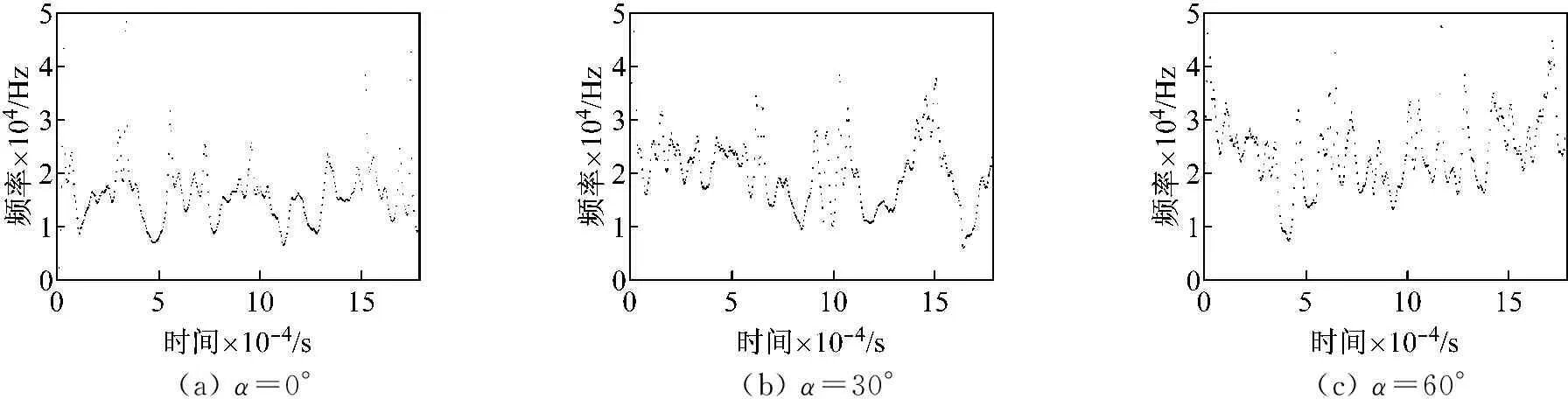
(a)α=0° (b)α=30° (c)α=60°
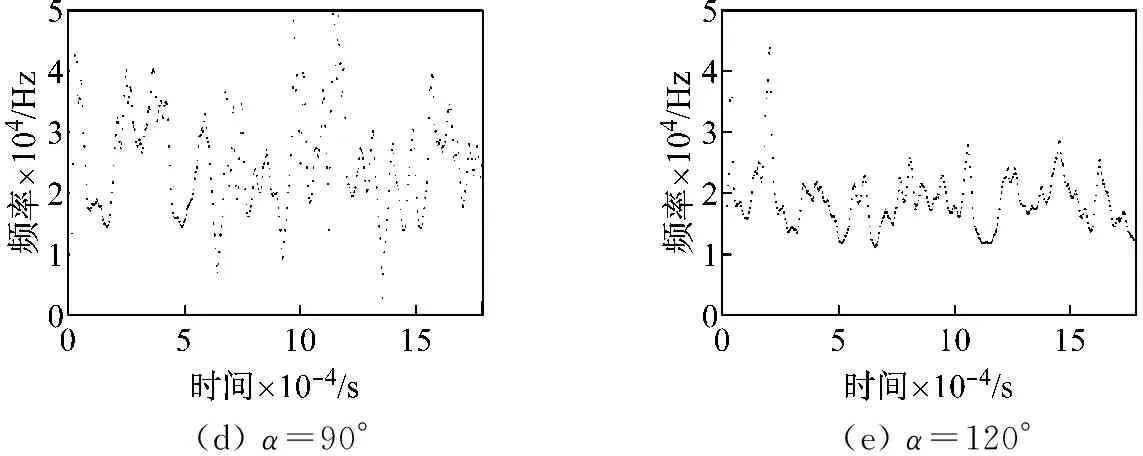
(d)α=90° (e)α=120°
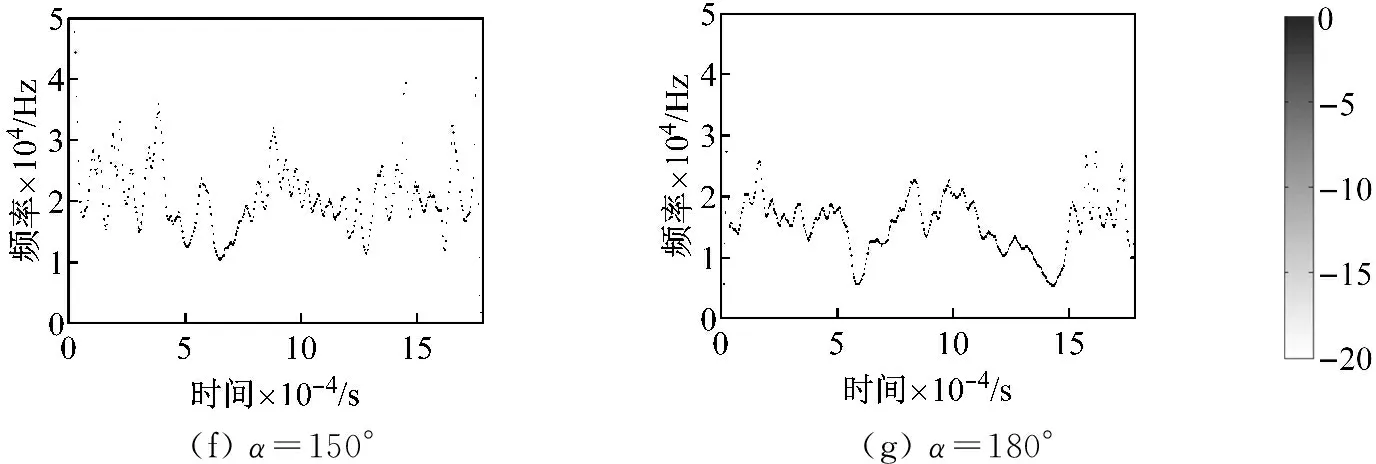
(f)α=150°(g)α=180°
图10 IMF5分量的希尔伯特谱图
Fig.10 The Hilbert spectrum of the fifth IMF component
5 结 论
(1) 电磁声发射是由于自由电子移动过程中促使流经路径中位错移动,并以声波能量的形式释放出来的物理过程,其与电磁加载条件有一定的关系,借助电磁加载方式可还原金属声发射信号特征。
(2) 电磁声发射信号为复杂的非线性、非平稳信号,采用HHT变换方法可以实现对电磁声发射信号在更高时频分辨率上的分析及评估,兼顾了可行性及高识别性。
(3) 利用水平磁场加载下电磁声发射表现的微观特性,结合IMF1~5分量的能量比值、相互关系数、IMF5分量的希尔伯特黄图,进一步阐明施加水平磁场角度的相对变化,将改变漂移电子运动过程中与位错势垒作用情况,进而影响电磁声发射信号特征,利IMF能量比值、互相关系数、特征IMF分量时频图分析裂纹的指向特征是可行的。
[1] SHEN Gongtian, WU Zhanwen, ZHANG Junjiao.Advances in acoustic emission technology[M].Springer Proceedings in Physics, New York, America,2015.
[2] FINKEL P, GODINEZ V, MILLER R, et al.echnique for damage evaluation[C].American Inst.of Physics Conf.Proc.,2001,557: 1747-1754.
[3] FINKEL P, GODINEZ V.Electromagnetic simulation of ultrasonic signal for nondestructive detection of ferromagnetic inclusions and flaws[J].IEEE Transactions on Magnetics, 2004, 40(4): 2179-2181.
[4] 刘素贞,金亮,张闯,等.电磁声发射检测技术的涡流激励方法[J].电工技术学报,2012,27(7):153-159.
LIU Suzhen, JIN Liang, ZHANG Chuang, et al.Eddy current exciting method for electromagnetically induced acoustic emission detecting technique[J].Trans.of China Electrotechnical Society, 2012, 27(7):153-159.
[5] 唐力伟,张晓涛,王平.管状金属构件裂纹电磁声发射激发特性试验研究[J].振动与冲击,2014,33(19):48-51.
TANG Liwei, ZHANG Xiaotao, WANG Ping.Tests for exciting features of electromagnetic acoustic emission of tubular metal parts’crack[J].Journal of Vibration and Shock, 2014, 33(19): 48-51.
[6] LEI Guana, TANG Guoyi, CHU P K.Recent advances and challenges in electroplastic manufacturing processing of metals[J] Journal of Materials Research, 2010, 25(7): 1215-1224.
[7] LI Dalong, YU Enlin, LIU Zhoutong.Microscopic mechanism and numerical calculation of electroplastic effect on metal’s flow stress[J].Materials Science and Engineering A, 2013, 580: 410-413.
[8] ANTOLOVICH S D.CONRAD H.The effects of electric currents and fields on deformation in metals, ceramics, and ionic materials: an interpretive survey[J].Materials and Manufacturing Processes, 2004, 19(4): 587-610.
[9] CONRAD H.Thermally activated plastic flow of metals and ceramics with an electric field or current[J].Materials Science and Engineering A, 2002, 322:100-107.
[10] GRONOSTAJSKI Z.The constitutive equations for FEM analysis[J].Journal of Materials Processing Technology, 2000, 106: 40-44.
[11] CHUNG J B, ASIBU E K.Acoustic emission from plastic deformation of a pure single crystal[J].Journal of Applied Physics, 1992, 72(5): 1812-1820.
[12] 刘贵杰,徐萌,王欣,等.基于HHT的管道阀门内漏声发射检测研究[J].振动与冲击,2012,31(23) :62-66.
LIU Guijie, XU Meng, WANG Xin, et al.AE detection for pipeline valve leaklage based on HHT[J].Journal of Vibration and Shock, 2012,31(23):62-66.
Characteristics analysis for EMAE and crack orientation under a horizontal magnetic field
CAI Zhichao1, LIU Suzhen2, ZHANG Chuang2, ZHANG Yanwei2, YANG Qingxin2,3
(1.School of Electrical and Automation Engineering, East China Jiaotong University, Nanchang 330013, China;2.Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability,Hebei University of Technology, Tianjin 300130, China; 3.Key Laboratory of Advanced Electrical Engineering and Energy Technology, Tianjin Polytechnic University, Tianjin 300387, China)
The key problem for the metallic structures’ health monitoring using the acoustic emission(AE) method is to establish a relationship between a suitable load and structures’ AE signals excited.But the current AE tests mostly use an offline loading on structures with the contact method.Here, an AE testing method using a contactless local electromagnetic online loading was proposed.Firstly, the mechanism of electromagnetically induced acoustic emission(EMAE) was studied at a microscopic level based on the electro induced dislocation and free electron movement theory.Secondly, the characteristic differences of EMAE signals under various electromagnetic loading conditions were studied, the emission characteristics of the collected nonstationary EMAE signals were studied with Hilbert-Huang transformation.Finally, the relationships among the energy percentage of intrinsic mode functions(IMFs), the cross-correlation coefficients of IMFs, the time-frequency figures of IMFs and crack orientation were established through changing the excitation direction of horizontal magnetic field.
electromagnetically induced acoustic emission; horizontal magnetic field; Hilbert-Huang transformation; crack orientation
国家自然科学基金(51307043)
2015-08-03 修改稿收到日期:2016-02-13
蔡智超 男,博士,讲师,1989年生
刘素贞 女,教授,博士生导师,1969年生
TM153
A
10.13465/j.cnki.jvs.2017.05.038
