横风下流线箱型桥-轨道交通车辆气动干扰风洞实验研究

邹云峰，何旭辉，郭向荣，何 玮，贺 俊

(1.中南大学 土木工程学院，长沙 410075； 2.高速铁路建造技术国家工程实验室，长沙 410075；3.中国建筑第五工程局有限公司，长沙 410004)

横风下流线箱型桥-轨道交通车辆气动干扰风洞实验研究

邹云峰1,2,3，何旭辉1,2，郭向荣1,2，何 玮1,2，贺 俊1,2

(1.中南大学 土木工程学院，长沙 410075； 2.高速铁路建造技术国家工程实验室，长沙 410075；3.中国建筑第五工程局有限公司，长沙 410004)

轨道交通车辆与桥梁间存在显著的气动干扰，但现有研究大多以流线型高铁车辆和钝体外形的简支梁桥为研究对象，且往往重点关注桥梁对车辆气动力大小的影响。以某流线箱型轨道专用桥和钝体外形的轨道交通车辆为背景，首先通过刚性节段模型测力试验，利用开发的车-桥系统气动力同步分离装置对不同风攻角、车桥组合方式下车辆和桥梁各自的气动力进行测试，分析横风下车桥间气动干扰对车辆、主梁和车桥系统所受总体气动力的影响规律；然后结合烟线法获得的车桥系统绕流场显示结果，揭示车桥间气动干扰机理。研究成果可为以后典型车桥组合工况下车、桥气动力经验公式的提出奠定基础，以及深入认识车桥间气动干扰机理提供参考。

横风; 流线箱型桥; 轨道交通车辆; 气动干扰; 车-桥系统; 风洞实验

为确保桥上列车在强风下运行的安全性和舒适性，通常需要进行风-车-桥耦合振动研究[1]。现有风-车-桥系统动力响应分析方法通常将车辆和桥梁作为两个动力子系统进行求解(车辆方程与桥梁方程由轮轨关系耦联)，为此需要输入车辆和桥梁各自的气动力[2]。对于风-车-桥系统而言，桥梁气动特性随列车的到达和离去而改变，桥上车辆则处于桥梁断面的绕流之中，车桥之间存在非常复杂的相互气动干扰，使得车-桥系统气动特性较单车、单桥时明显不同[3]。事实上，日本早在1986年调查山阴线餘部桥上的翻车坠桥事故发生原因时便指出必须将列车和桥梁作为整体系统进行气动特性综合分析[4]。然而，目前规范中规定的桥梁风荷载为桥梁独自存在时受到的风荷载，对车辆也是如此。忽略车桥间存在的相互气动干扰作用，将导致风-车-桥耦合振动分析结果产生较大的误差。随着轨道交通尤其是高速铁路的迅速发展，车桥间的相互气动干扰受到了国内外学者关注，并进行了广泛而深入的研究[5-12]。但这些研究大多以流线型高铁车辆和钝体简支梁桥为研究对象，且通常仅关注桥梁对列车气动力大小的影响，而忽略了车辆对桥梁气动力的干扰。这是因为现有高铁桥梁大多以简支梁桥为主(例如，京沪高铁90%以上桥梁为简支梁)，此类桥梁跨度小、刚度大，对风荷载不敏感。然而，研究表明[13-14]，即使是外形较钝化的简支梁桥，车辆紧贴在桥面运行时会显著改变主梁的绕流场，车辆对主梁气动力的影响不容忽略。随着轨道交通事业的发展，轨道交通桥梁跨度不断增长，主梁往往采用流线型外形以提高大跨桥梁的抗风稳定性，车辆对流线型桥梁的气动影响较钝体桥梁必将愈加突出，影响规律可能也会不同。

本文以某流线箱型轨道专用桥和钝体外形的轨道交通车辆为背景，通过开发的车-桥系统气动力同步分离装置对不同风攻角、车桥组合方式下车辆、桥梁各自的气动力进行测试，并尝试利用烟线法对车桥系统的绕流场进行显示，结合两种方法对车桥气动干扰进行深入研究。基于试验结果，分析研究车桥组合对车辆和桥梁气动特性的影响规律以及影响原因，为今后典型车桥组合工况下车、桥气动力经验公式的提出奠定基础。

1 气动力测试概况

本文研究的列车原型为国家标准地铁A型车，桥梁为主跨340 m的双塔双索面流线箱型斜拉桥。由于列车通常由多节车厢组成，长度较大，可认为它与大跨桥梁一样，近似符合条带假定，因此列车和桥梁的气动力都可通过节段模型测力风洞试验得到[15]。结合风洞试验段几何尺寸，为满足堵塞率等风洞试验要求，模型几何缩尺比选为1∶40，桥梁和列车模型长度均为2.0 m(桥梁模型长宽比为4.08)，最大堵塞率为4.1%(小于规范规定的5%，可忽略堵塞率对试验结果的影响)，模型横截面尺寸如图1所示。试验模型采用优质木材制作，并在主梁和列车模型内部均设置了加劲梁，保证模型具有足够的强度和刚度，在试验中模型不发生变形且不出现明显的振动以保证测试精度。

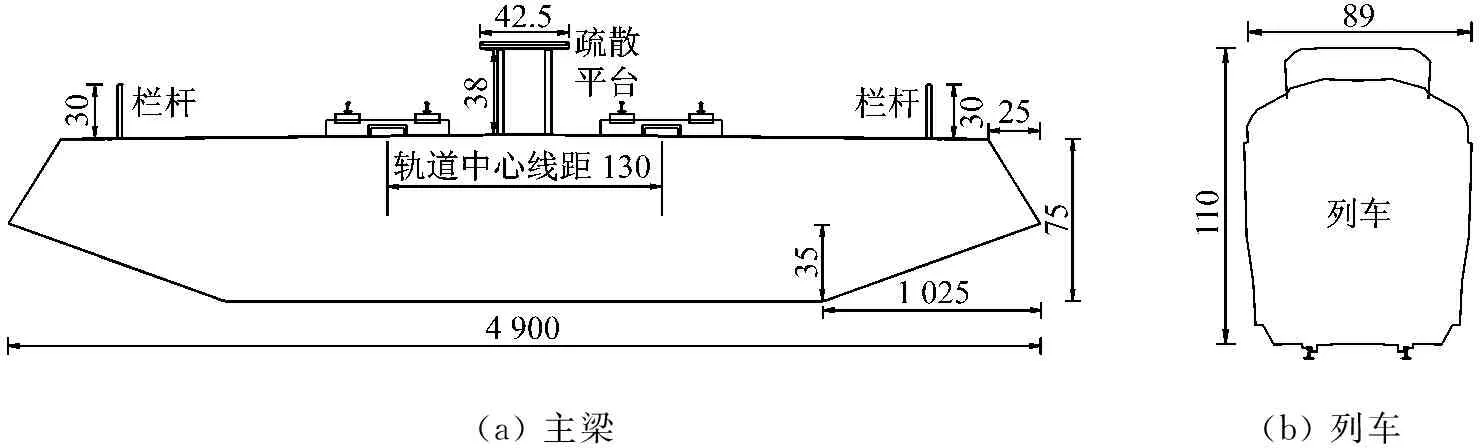
(a)主梁(b)列车

图1 模型横断面(mm)

Fig.1 Geometric dimensions of the model (mm)

为同步测试车-桥系统中车辆和桥梁各自的气动力，本文开发的测力装置如图2所示，列车和桥梁模型水平固定在可转动圆盘上，二者之间有一定的间隙(车轮高度)以实现气动力分离；在列车和桥梁模型两端都装有动态测力天平(共安装(模型数×2)个天平，模型两端天平数据之和便为该模型受到的气动力)，专用数据采集软件可把各天平采集到的数据同步记录在电脑上；列车可沿滑杆水平移动，而滑杆可沿弧形滑槽上下移动，进而实现列车相对桥梁几何位置的调整；圆盘、列车和桥梁可绕桥梁端部的测力天平做同轴转动，以便于风攻角的调节，为保证风攻角调节精度，在圆盘上设计了定位孔，通过固定不同的定位孔可精确调节风攻角；测力装置由固定在风洞地板上的竖向支撑系统支撑，支撑系统的间距可根据模型长度调节。使用的动态测力天平为日本NITTA公司生产的IFS型六分量动态天平，测力分辨率为0.02 N，本次试验采样频率设定为1 kHz，采样时长30 s。

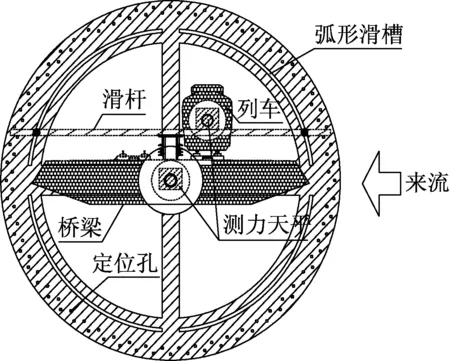
图2 测力装置示意图Fig.2 Schematic diagram of dynamometric device

风洞试验在“高速铁路建造技术国家工程实验室”的高速铁路风洞试验系统进行，该系统包括高速和低速两个试验段，其中，高速试验段长15.0 m，宽3.0 m，高3.0 m，试验风速在0～94 m/s范围内连续可调；低速试验段长18.0 m，宽12.0 m，高3.5 m，试验风速在0～20 m/s范围内连续可调。本次试验在高速试验段内的均匀流场中完成。研究表明[16]，横风下列车气动特性为最不利，因此仅考虑风向角α=90°，即来流方向与桥纵向垂直。表1所列为本文试验工况安排，共进行约130个吹风工况。

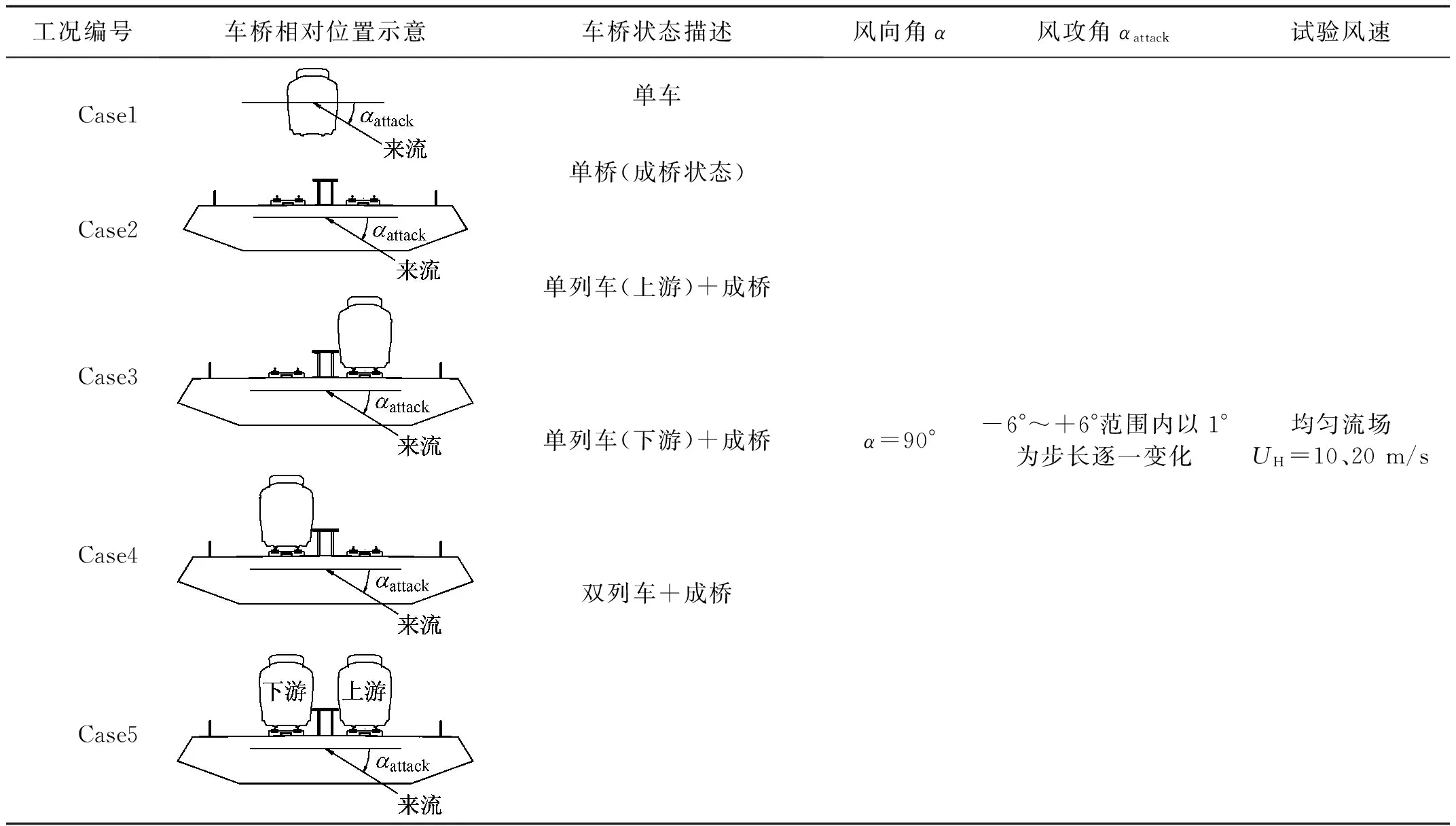
表1 测试工况Tab.1 Test case

2 数据处理

空气动力学中常用三分力系数描述结构气动特性，有体轴和风轴两种坐标系表达方式，但二者可相互转换，故仅给出体轴坐标系下的测试结果。体轴坐标系下侧力系数CD(t)、升力系数CL(t)和力矩系数CM(t)的定义分别如下[11]：

(1)

(2)

(3)

式中：FD(t)、FL(t)、M(t)分别为体轴系下模型受到的侧力、升力和力矩时程，各气动力方向规定见图3(图中，αattack为风攻角，试验中可通过模型的转动实现，本文规定以绕来流方向顺时针方向转角为正)，对其进行时间平均可得到平均值；H，B，L分别为模型的高、宽、长，具体数值可参见图1；UH为参考点风速，由眼镜蛇探针测试得到，参考点高度与主梁模型安装位置高度相当。

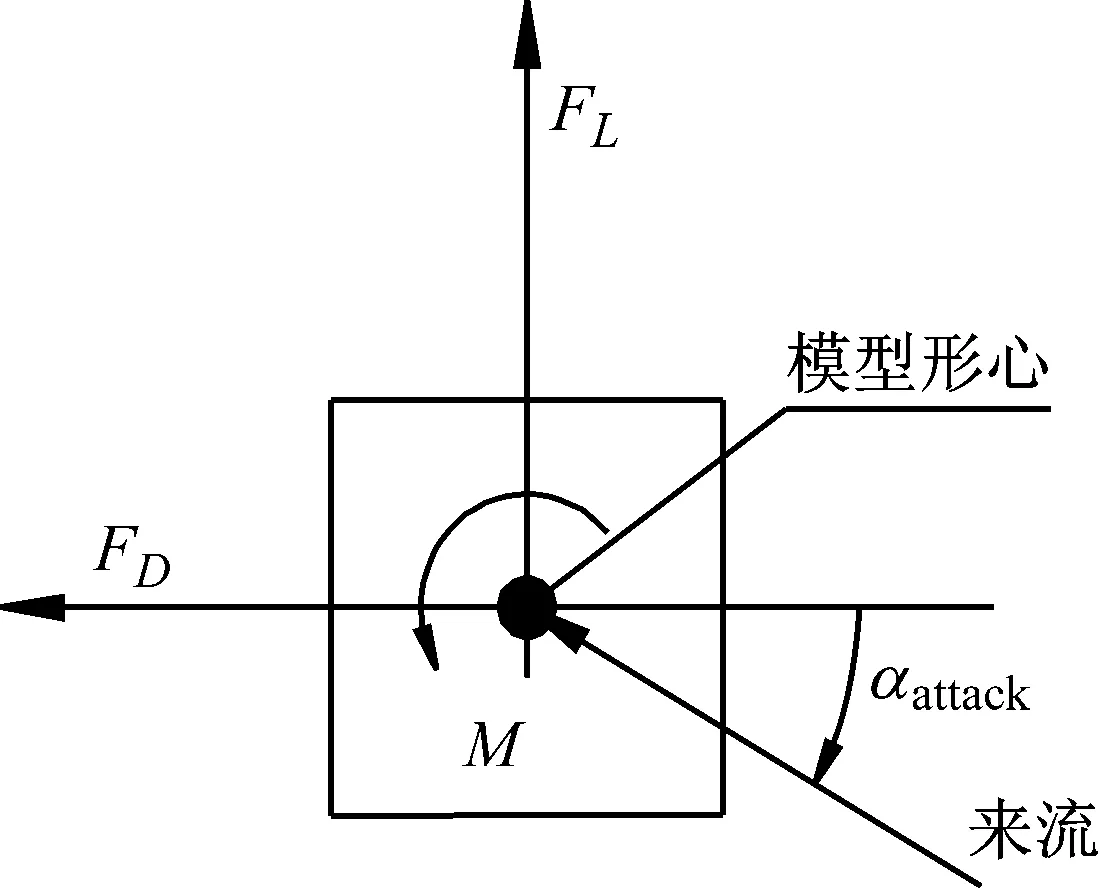
图3 体轴坐标系下气动力示意图Fig.3 Aerodynamic force in body axis

为直观的比较车桥组合工况下列车、桥梁气动力与车、桥独自存在时的差异，本文直接给出车桥组合工况列车、桥梁气动力均值与单车、单桥时的比值。

3 气动力测试结果分析

对两种试验风速(UH=10 m/s,UH=20 m/s)下各

工况列车、桥梁气动力测试结果对比发现，雷诺数对试验结果的影响较小，车桥组合工况(Case3～Case5)气动特性的雷诺数效应更为微弱。其原因在于，列车外形呈钝体断面，其绕流分离点较为固定，车桥组合时，主梁分离流中的脉动成分减小了列车绕流的黏性作用，进一步弱化了列车气动特性的雷诺数效应；对于桥梁而言，桥上附属构件(栏杆、疏散平台等)钝化流线型断面，车辆与主梁组合后则形成更为钝化的系统。考虑到高风速时模型可能存在一定程度的振动，导致测试结果有一定误差，因此后文分析中以UH=10 m/s的测试结果为准。

3.1 车辆气动力

图4所示为车桥组合状态下列车气动力系数与单车时的比值。从图4(a)可看出，Case5的下游车辆侧力系数最小，为接近0的负值，这是因为测试列车几乎完全处于上游车辆的“遮挡效应”中。尽管Case5上游车辆的尾流脱落受下游车辆干扰，但其侧力系数仅略小于Case3，表明Case5下游车辆对上游车辆的气动干扰影响较小，这一结果与文献[13-14]的研究结论一致。Case3和Case5上游车辆0°攻角附近的侧力略大于单车，这可能是因为主梁的存在加大列车尾流宽度，增强车辆背风面负压进而增大列车空气侧力；随着攻角的变大，前述效应逐渐减弱，而主梁的遮挡效应加强，故侧力系数逐渐变小；当攻角大于3°后，主梁的遮挡效应不再增强，列车侧力随攻角变化趋于稳定，约为单车的85%。Case4的测试列车位于下游轨道，由于轨道距桥梁前缘较远，车辆处于桥梁前缘分离产生的低速区，故其侧力系数较单车小，约为单车的70%，且由于它始终处在桥梁分离的尾流中，其侧力受风攻角变化影响较小。

由图4(b)可知，各工况下车辆升力随攻角变化的趋势基本一致，尽管大多风攻角下车辆升力系数幅值小于单车(比值小于1)，但车辆的升力方向发生变化(比值为负值)，由于单车状态的升力为负(方向定义参见图3)，即意味着车桥组合下列车受到向上的浮力，可能增大轮重减载率，不利于行车安全。Case5下游车辆由于上游列车遮挡导致升力较小，大小约为单车的0.1倍。Case3、Case4和Case5上游车辆升力分别为单车的0.33、0.66和0.48倍，Case3和Case4比较而言，Case4车辆位于下游轨道，距桥梁前缘分离点更远，车辆可能完全处于桥梁前缘分离产生的低速区，在列车顶面产生较大的负压，故升力较大；Case3和Case5上游车辆比较而言，Case5上游车辆尾流脱落受下游车辆干扰可能是导致其升力大于Case3的原因。在风攻角小于-4°后，各工况升力比值出现突然增大现象，这是因为这些风攻角下单车的升力很小，从而导致较大比值，故笔者认为这些大值没有参考意义。

从图4(c)可看出，车桥组合时，列车受到的力矩小于单车，Case3、Case4和Case5上游车辆力矩大小相当，而Case5下游车辆最小，表明列车所在轨道位置对其力矩影响较小，受列车的遮挡效应影响较大。由于力矩是侧力和升力大小及其作用位置共同影响的结果，其随攻角变化并无明显规律。

(a) 侧力系数比值

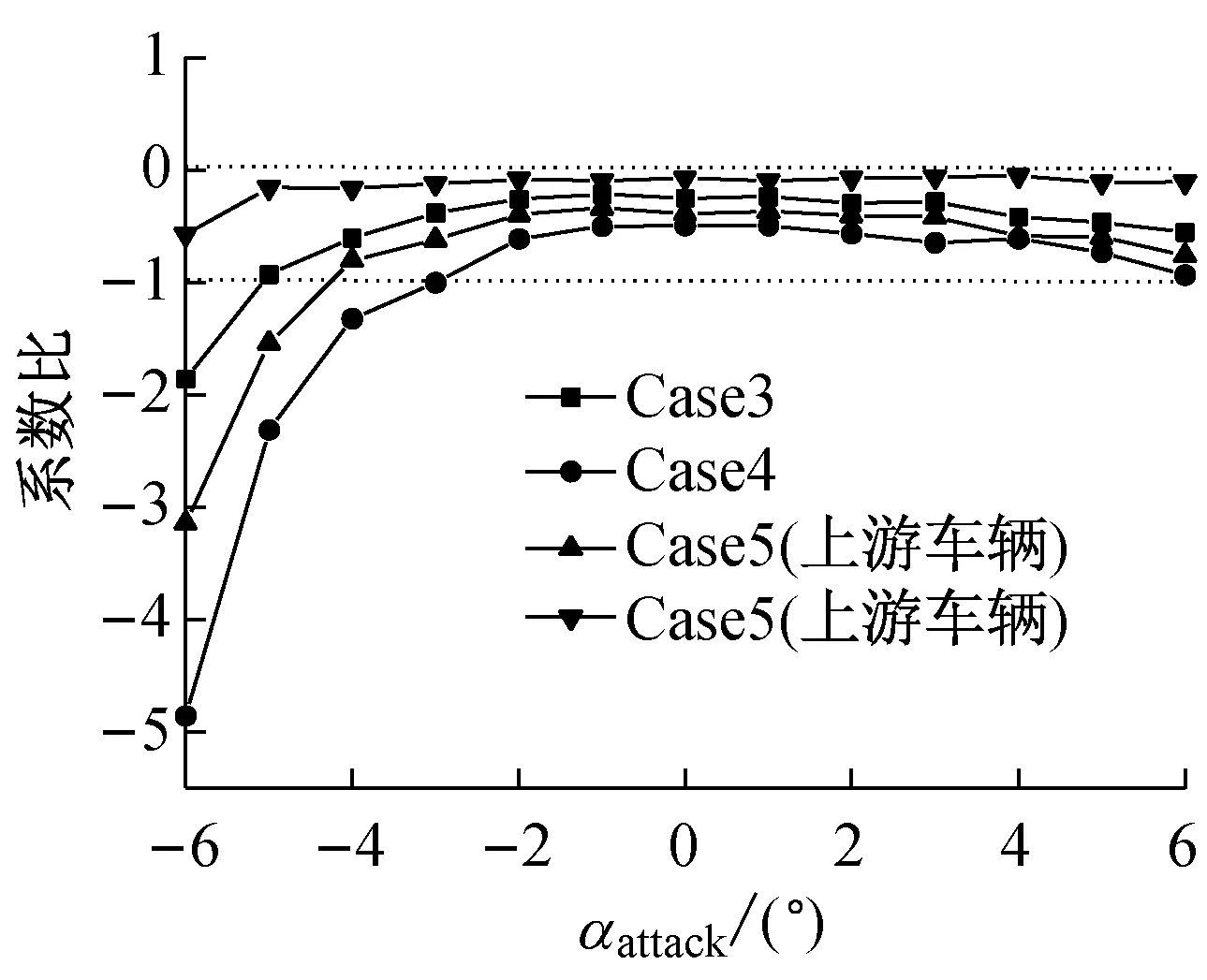
(b) 升力系数比值

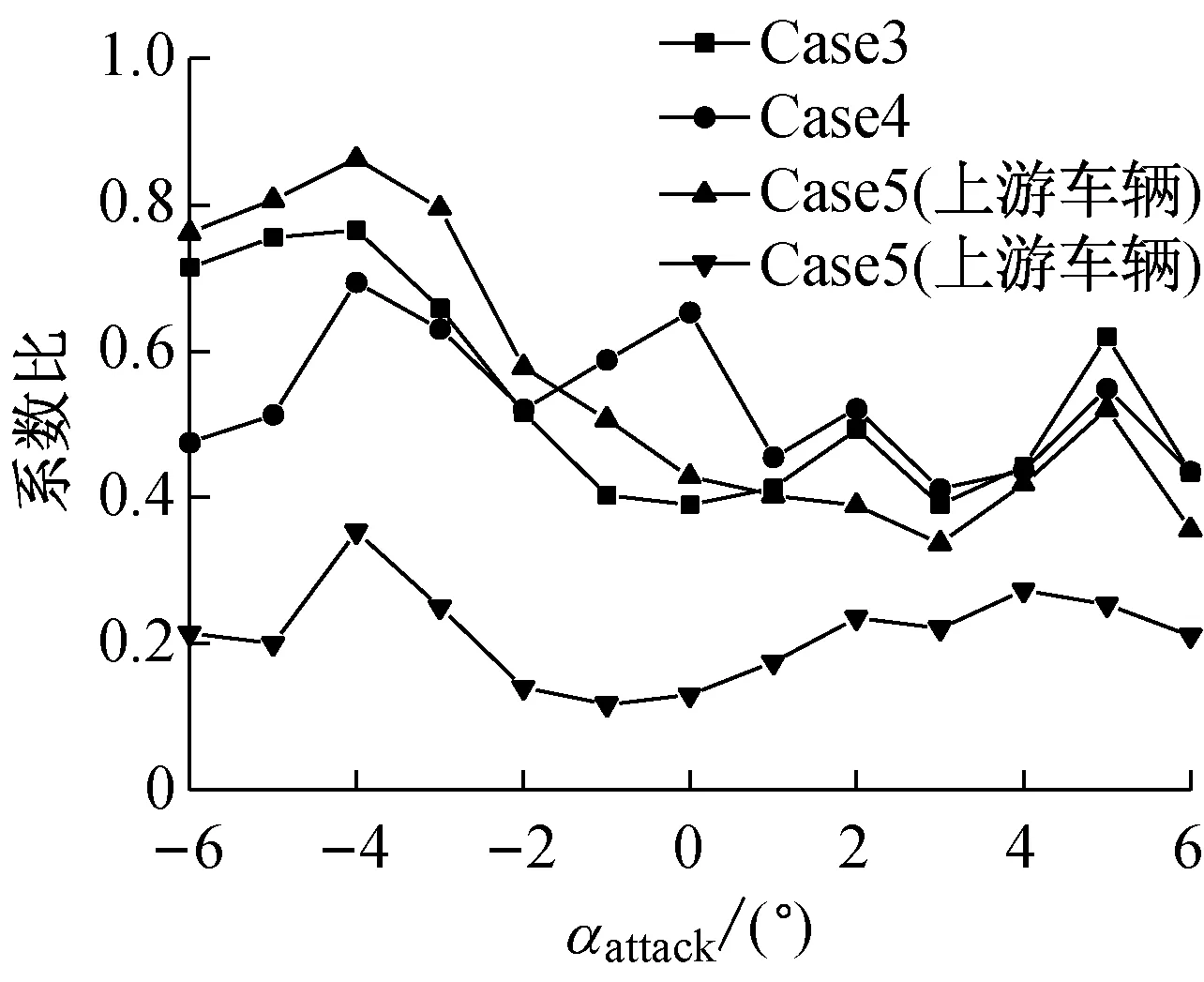
(c) 力矩系数比值

3.2 主梁气动力

图5所示为主梁气动力系数比值。从图5可看出，Case3和Case4桥梁的气动力结果差异很大，表明车桥组合状态下列车对桥梁绕流场的影响与其所处的轨道位置密切相关；Case3和Case5桥梁的气动力结果基本一致，意味着当上游轨道有列车时，下游轨道上列车对桥梁绕流场的影响几乎可以忽略。当列车位于上游轨道时(Case3和Case5)，风攻角大于-4°以后，主梁侧力随攻角增加而大致呈线性增大，并在3°攻角以后大于桥梁独自存在时的侧力(图5(a))；在±6°攻角范围内，车桥组合状态下桥梁受到的升力均较桥梁独自存在时的大，并随攻角增加而增大(图5(b))。当列车位于下游轨道时(Case4)，桥梁侧力随风攻角的增加而呈线性减小，并在攻角小于+3°范围内较单桥大；桥梁受到的升力随风攻角的增加而减小，且方向与单桥时相反，并在攻角大于+2°后，升力大小也大于单桥。需要指出的是，升力随风攻角的增加而减小意味着升力系数关于攻角的斜率为负，即下游列车的存在可能对该桥的驰振稳定性产生不利影响。

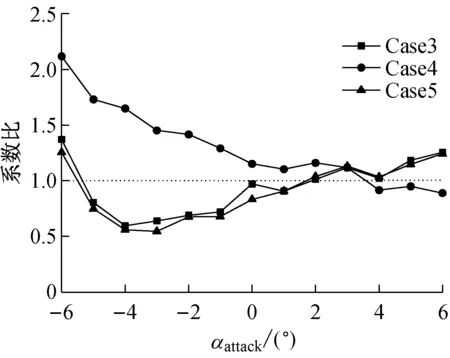
(a) 侧力系数比值

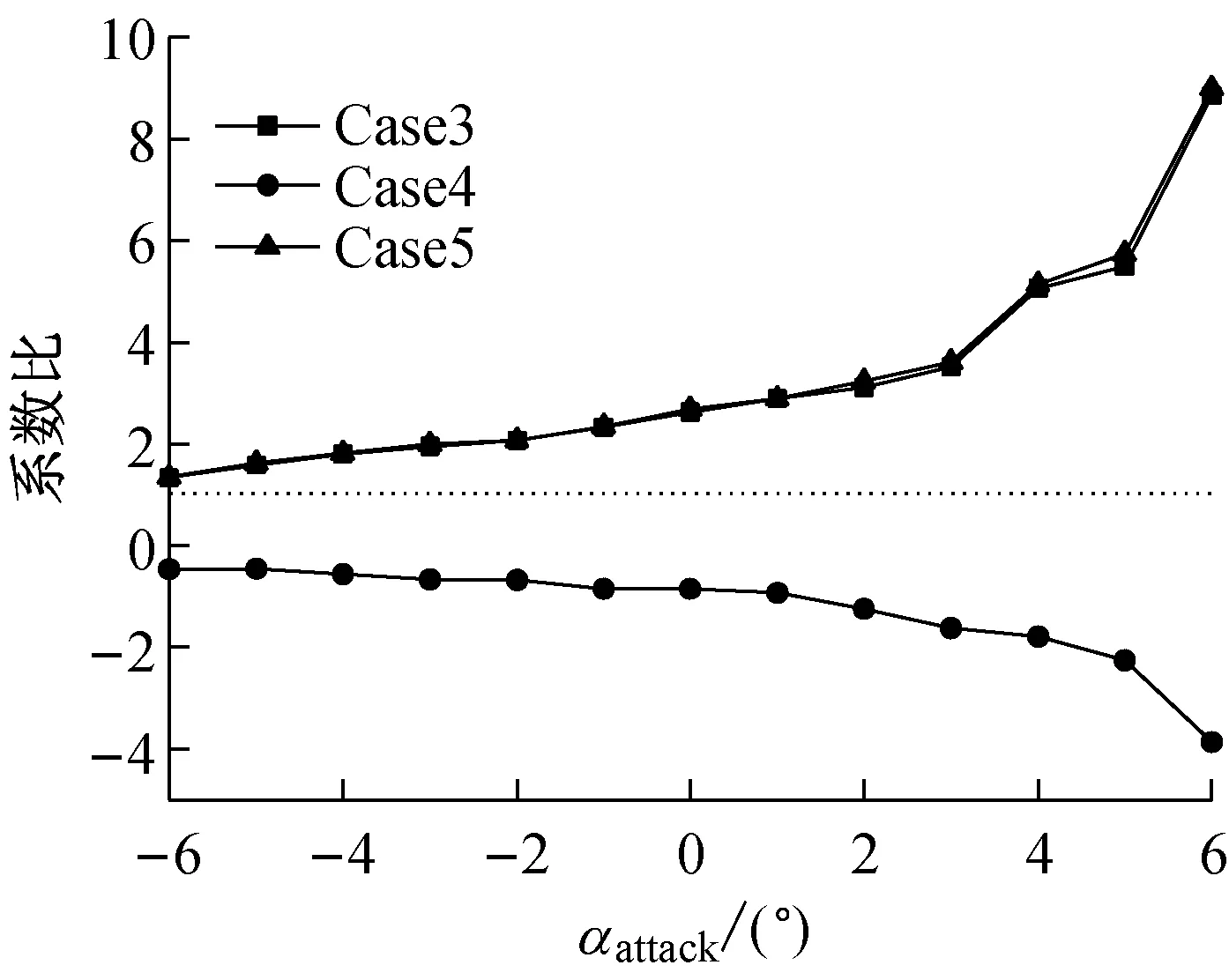
(b) 升力系数比值

3.3 车桥系统气动力

车桥系统实际运行中，列车受到的风荷载将通过轨道传递给桥梁，因此在对桥梁进行抗风设计时需要考虑车桥系统所受的总体气动力大小。尽管前文对各车桥组合工况下列车和桥梁各自的气动力大小变化进行了较详尽的分析，但由于列车和桥梁的特征几何尺寸不同，将桥梁和列车的力系数直接简单相加不能反映车桥系统总体气动力大小的变化情况，为此本文将列车的气动力系数进行转换。列车侧力系数CD,T转换过程如下：

综上所述，文化因素、社会因素、个人因素与少数民族大学生创业能力均呈现显著正相关关系，对其创业能力的提升都起着重要作用，这为少数民族大学生创业能力的有效提升提供了参考价值。

(4)

式中：HT、LT分别为列车模型的高和长，HB、LB分别为主梁模型的高和长。

由式(4)可看出，将列车侧力系数CD,T乘以转换系数(HTLT/HBLB)后，它与桥梁侧力系数之和可反映车桥系统所受总体侧力大小。同理，可将列车升力做类似转换。最终根据图1中模型几何尺寸，可得列车侧力和升力的转换系数分别为1.47和0.02。

图6所示为车桥系统总体气动力系数比值随攻角变化情况。从图6(a)可看出，车桥组合大大增加桥梁所受的侧力，最小值也为单桥时的1.75倍，这是因为车辆高度较主梁大，车辆所受侧力占车桥系统总侧力的比重大，车辆的存在大大增加车桥系统的侧力；Case3和Case5下的侧力随攻角变化趋势基本一致，其原因可能为这两种工况下均以上游车辆对车桥系统绕流场干扰为主，但Case5由于下游车辆负侧力的出现及其对上游车辆漩涡脱落的干扰，使得该工况的侧力较Case3略小；Case4由于以下游车辆对车桥系统绕流流场干扰为主，故其侧力随攻角变化趋势较其它工况明显不同。对于车桥系统升力而言，图6(b)与图5(b)基本一致，这是因为车辆升力仅为主梁的2%，车辆对车桥系统升力贡献较小。

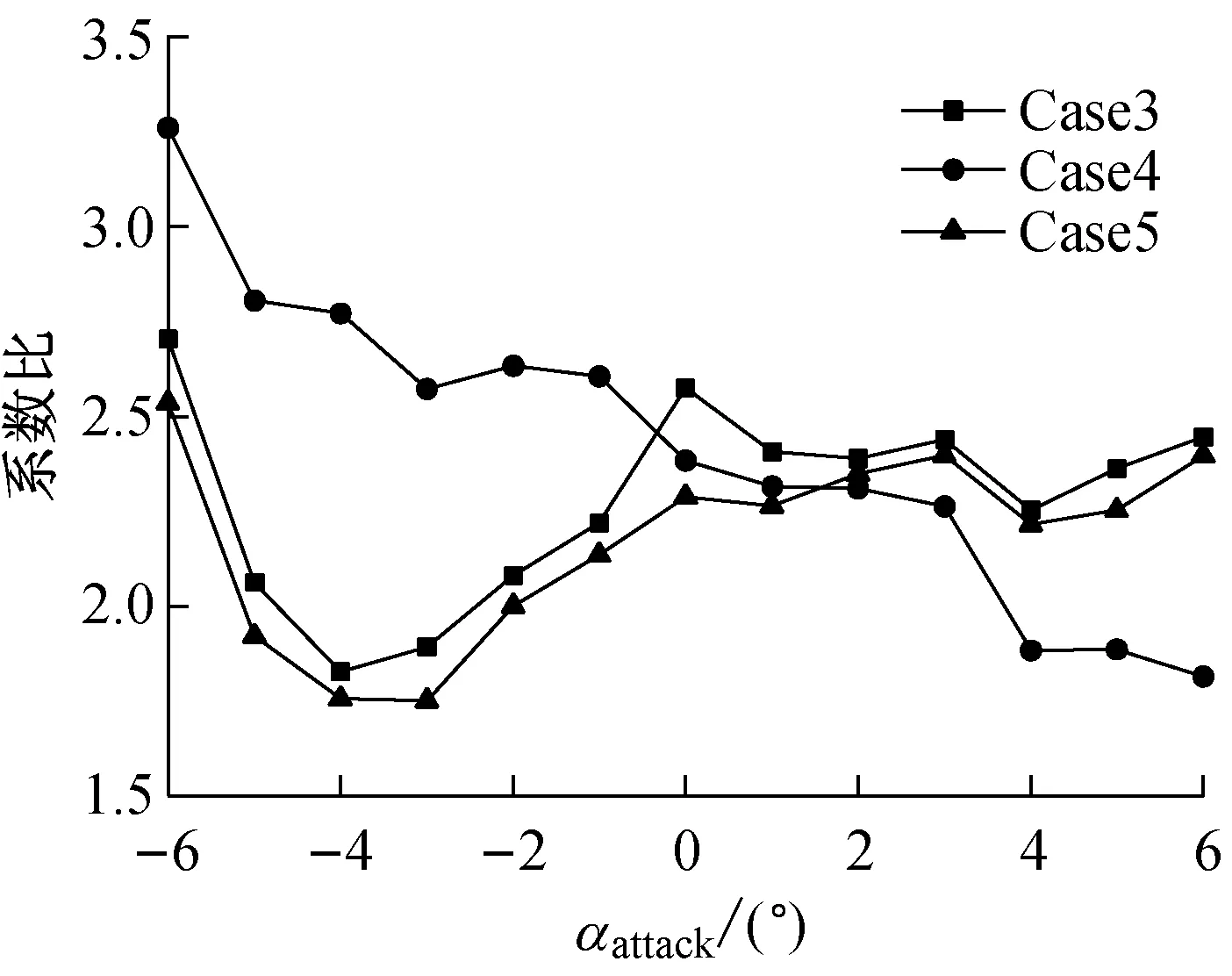
(a) 侧力系数比值

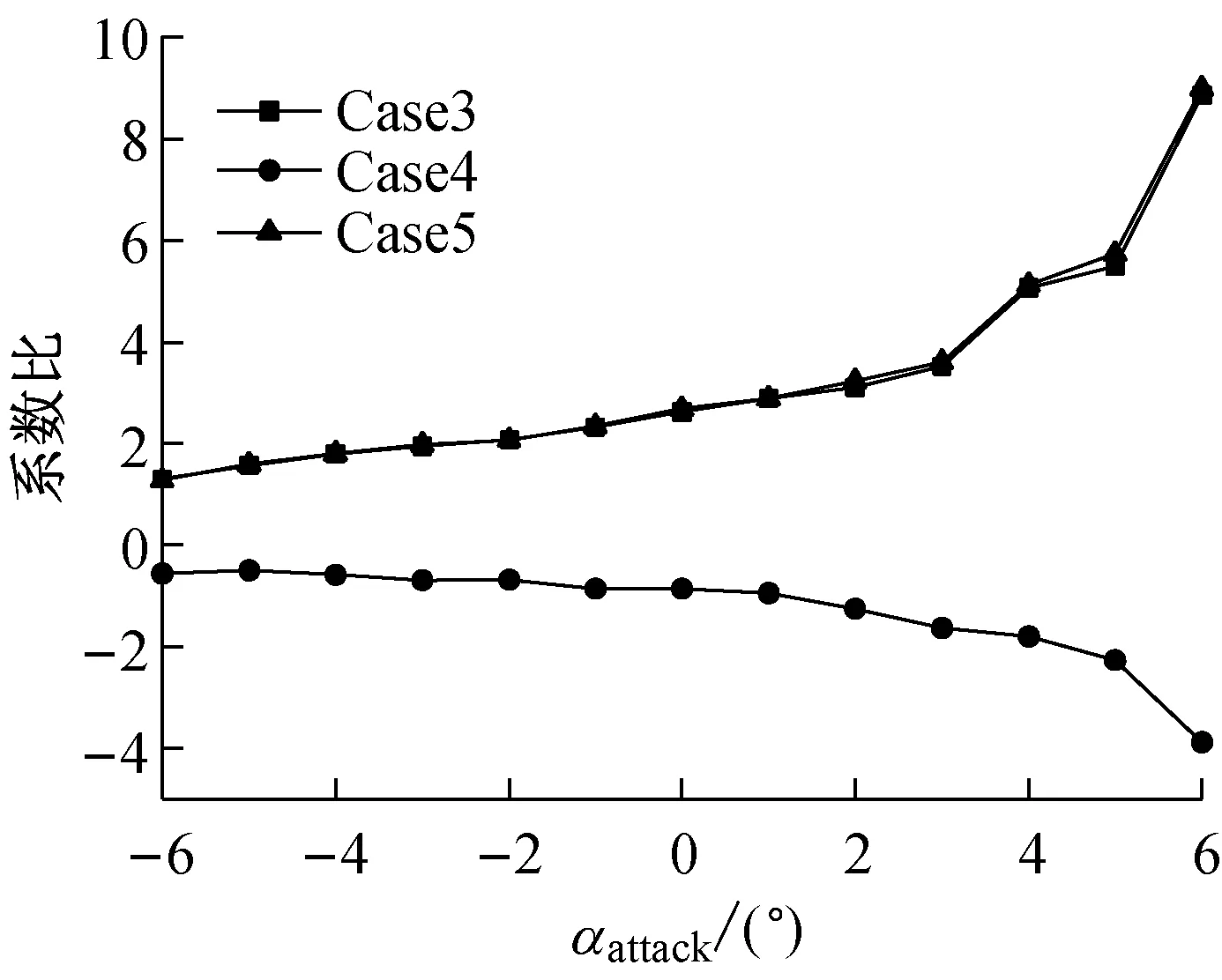
(b) 升力系数比值

4 车桥系统流场显示结果

为深入认识车桥系统气动干扰机理，尝试通过烟线法流场显示风洞试验获得车桥系统气流绕流场。实验在中南大学开口直流式小型风洞中进行，试验段尺寸为高×宽×长=0.45 m×0.45 m×1.0 m，风速范围为0～42 m/s，湍流度小于0.6%。实验采用的流场显示仪器为航华烟线仪，利用ATMEGA单片机对电容的充、放电和相机拍照进行控制，具有电流大，时间和电流控制精确等特点[17]。通过不同大小模型、风速下流场显示结果对比(模型长度与风洞宽度保持一致，为0.45 m)，发现几何缩尺比为1∶150、试验风速为4 m/s时效果最佳。为简化流场以更为显著的对比车桥间绕流场的气动干扰，试验中未考虑栏杆等主梁附属物对流场的影响，并只考虑0°风攻角。

由图7(a)和图7(b)可看出，车辆外形较钝化，其分离点固定，故车辆气动特性的雷诺数效应较弱；反之，主梁绕流呈明显流线型特征；车桥组合后，车桥系统绕流场的分离点固定，呈明显的钝体特征。将图7(c)和图7(d)与图7(a)和图7(b)对比，可发现上游车辆处于桥梁前缘分离产生的尾流区，迎风面气流速度降低，但由于车桥系统绕流场的尾流宽度增加，使车辆背风面的负压增强，可能由于背面风负压增强幅度大于迎风面气流速度降低幅度，进而导致该攻角下上游车辆的侧力略大于单车；列车底部绕流由于车辆处于主梁尾流中而减弱，进而导致车底负压减弱，而车顶负压受主梁前缘分流的影响而增强，导致车桥组合下车辆受到向上的升力。对于主梁而言，车辆的存在主要影响主梁上部绕流场及尾流漩涡脱落，尽管车桥系统尾流涡脱宽度较单桥大大增加，但上游车辆的存在使来流受阻并使其流速降低，故主梁侧力较单桥略有减小；尽管主梁底部绕流场受车辆影响较小，但由于桥上车辆固定的气流分离点使得主梁上表面负压大大增强，因此主梁升力较单桥时大。

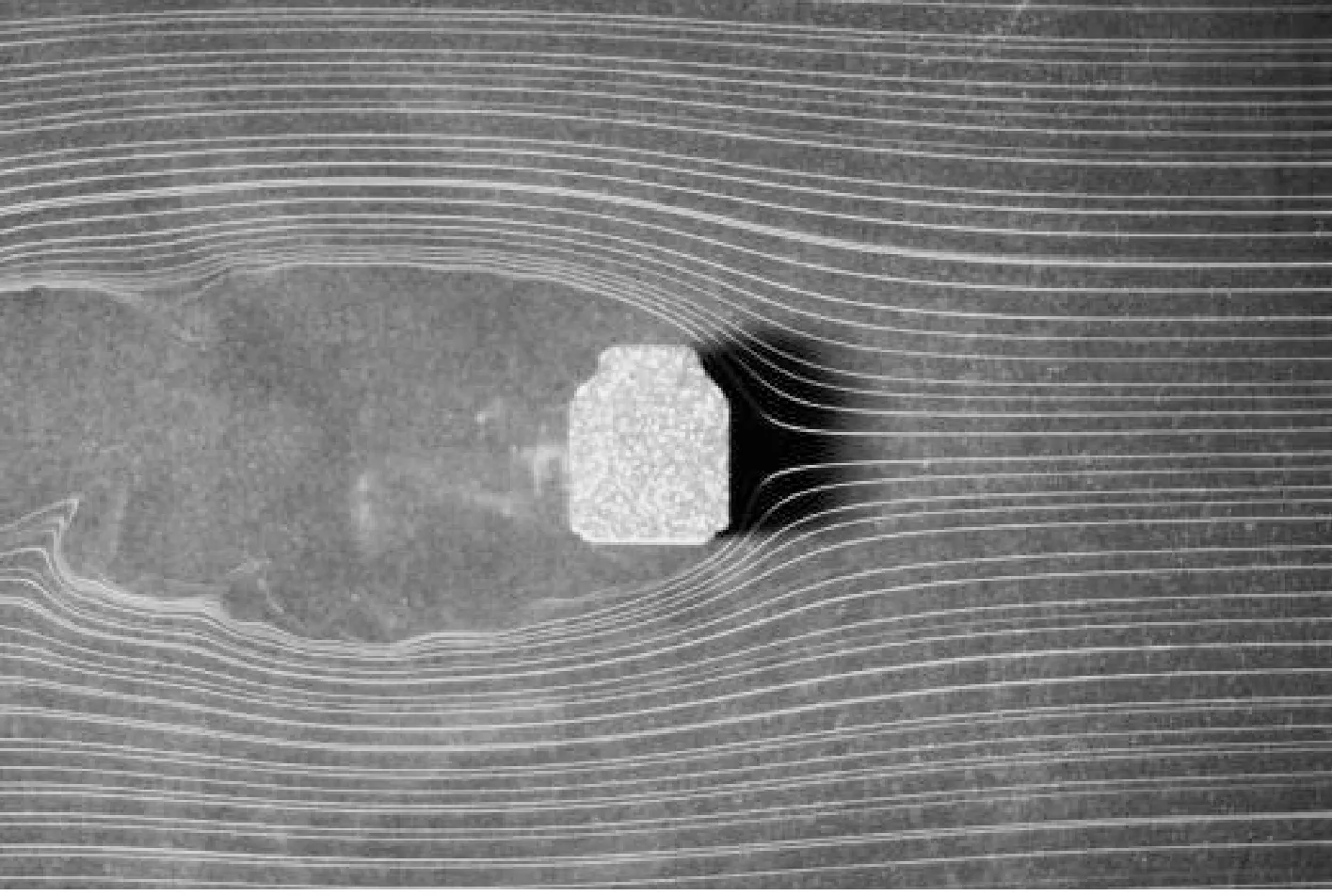
(a) Case1

(b) Case2

(c) Case3

(d) Case5

5 结 论

本文以流线箱型桥和轨道交通车辆为背景，结合刚性节段模型测力和流场显示风洞试验对横风下车桥系统的气动干扰进行研究，通过对比分析得到的主要结论如下：

(1) 即使对于流线型桥梁，车桥组合使得车-桥系统绕流场分离点固定，其绕流特性呈典型钝体特性，即可忽略雷诺数效应对车-桥系统气动特性的影响。

(2) 车桥组合使大多风攻角下的车辆侧力减小，上游车辆约为单车的85%，下游车辆约为单车的70%；各车桥组合方式下车辆升力随攻角变化趋势基本一致，尽管升力大小大多小于单车，但方向与单车相反，即列车受到向上的浮力，可能增大轮重减载率，不利于行车安全。

(3) 车桥组合使主梁升力增大，且升力斜率可能为负，即对该桥的驰振稳定性产生不利影响；尽管主梁侧力可能减小，但由于车辆高度大，车辆所受侧力与桥梁相当甚至偏大，经轨道传递至桥梁的车辆侧力将大大增加横向静风引起大桥侧倾失稳的可能性，即需要注意车辆对大桥静风稳定检验风速的影响。

(4) 流场显示结果表明，车桥组合时，车辆处于桥梁前缘分离产生的低速区，迎风面和车底绕流气流速度降低；对于主梁而言，车辆的存在使来流受阻并降低流速。车桥系统尾流宽度较单车、单桥时大大增加，使车辆与主梁背风面和车顶的负压增强。车、桥气动力变化情况取决于结构物表面绕流气流速度降低幅度与负压增强幅度之差。

[1] 金学松, 郭俊, 肖新标, 等.高速列车安全运行研究的关键科学问题[J].工程力学, 2009, 26(增刊2):8-22.

JIN Xuesong, GUO Jun, XIAO Xinbiao, et al.Key scientific problems in the study on running safety of high speed trains[J].Engineering Mechanics, 2009, 26(Sup2):8-22.

[2] 夏禾, 张楠, 郭薇薇, 等.车桥耦合振动工程[M].北京: 科学出版社, 2014.

[3] 李永乐.风-车-桥系统非线性空间耦合振动研究[D].成都: 西南交通大学, 2003.

[4] 刘庆宽.强风环境下列车运行安全保障体系的初步研究[J].工程力学, 2010, 27(增刊1):305-310.

LIU Qingkuan.Study on the system to ensure train operation safety under strong wind[J].Engineering Mechanics, 2010, 27(Sup1):305-310.

[5] 何旭辉, 邹云峰, 杜风宇.风屏障对高架桥上列车气动特性影响机理分析[J].振动与冲击, 2015, 34(3): 66-71.

HE Xuhui, ZOU Yunfeng, DU Fengyu.Mechanism analysis of wind barrier’s effects on aerodynamic characteristics of a train on viaduct[J].Journal of Vibration and Shock, 2015, 34(3): 66-71.

[6] SUZUKI M, TANEMOTO K, MAEDA T.Aerodynamic characteristics of train/vehicles under cross winds[J].Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(1):209-218.

[7] 葛玉梅, 李永乐, 何向东.作用在车-桥系统上风荷载的风洞试验研究[J].西南交通大学学报, 2001, 36(6): 612-616.

GE Yumei, LI Yongle, HE Xiangdong.Study on wind-induced loads of train-bridge system by wind tunnel test[J].Journal of Southwest Jiaotong University, 2001, 36(6): 612-616.

[8] 祝志文, 陈政清.单、双层客车车辆在铁路桥梁上的横向气动力特性[J].中南工业大学学报(自然科学版), 2001, 32(4): 410-413.

ZHU Zhiwen, CHEN Zhengqing.Aerodynamic characteristics of single and double-deck vehicle passing the railway bridges in cross-wind[J].Journal of Central South University of Technology, 2001, 32(4): 410-413.

[9] CHELI F, CORRADI R, ROCCHI D, et al.Wind tunnel tests on train scale models to investigate the effect of infrastructure scenario[J].Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(6/7): 353-362.

[10] 高广军, 苗秀娟.强横风下青藏线客车在不同高度桥梁上的气动性能分析[J].中南大学学报(自然科学版), 2010, 41(1): 376-380.

GAO Guangjun, MIAO Xiujuan.Aerodynamic performance of passenger train on different height of bridge of Qinghai-Tibet railway line under strong cross wind[J].Journal of Central South University(Science and Technology), 2010, 41(1): 376-380.

[11] HE X H, ZOU Y F, WANG H F, et al.Aerodynamic characteristics of a trailing rail vehicles on viaduct based on still wind tunnel experiments[J].Journal of Wind Engineering and Industrial Aerodynamics, 2014, 135:22-33.

[12] 韩艳, 胡揭玄,蔡春声, 等.横风下车桥系统气动特性的风洞试验研究[J].振动工程学报, 2014, 27(1): 67-74.

HAN Yan, HU Jiexuan, CAI Chunsheng, et al.Wind tunnel measurement on aerodynamic characteristics of vehicles and bridges under cross winds[J].Journal of Vibration Engineering, 2014, 27(1): 67-74.

[13] 李永乐, 向活跃, 侯光阳, 等.车桥组合状态下CRH2客车横风气动特性研究[J].空气动力学学报, 2013, 31(5):579-582.

LI Yongle, XIANG Huoyue, HOU Guangyang, et al.Aerodynamic characteristics of CRH2 train in combination of vehicle-bridge with cross wind action[J].ACTA Aerodynamic Sinica, 2013, 31(5):579-582.

[14] 李永乐, 周昱, 葛世平, 等.主梁断面形状对车-桥系统气动特性影响的风洞试验研究[J].土木工程学报, 2012, 45(7): 135-141.

LI Yongle, ZHOU Yu, GE Shiping, et al.Wind tunnel test study of the effect of bridge deck cross section shape on aerodynamic characteristics of vehicle-bridge system[J].China Civil Engineering Journal, 2012, 45(7): 135-141.

[15] 李永乐, 廖海黎.线状多体系统定常气动力节段模型风洞测试[J].流体力学实验与测量, 2004，18(2):91-94.

LI Yongle, LIAO Haili.Section model wind tunnel test for steady aerodynamic force of line-like multi-body system[J].Experiments and Measurements in Fluid Mechanics, 2004, 18(2):91-94.

[16] 何旭辉, 邹云峰, 周佳, 等.运行车辆风环境参数对其气动特性与临界风速的影响[J].铁道学报, 2015, 37(5): 1-6.

HE Xuhui, ZOU Yunfeng, ZHOU Jia, et al.Effect of wind environment parameters on aerodynamic characteristics and critical wind velocity of vehicle operation[J].Journal of the China Railway Society, 2015, 37(5): 1-6.

[17] 崔尔杰, 洪金森.流动显示技术及其在流体力学研究中的应用[J].空气动力学学报, 1991, 9(2): 190-199.

CUI Erjie, HONG Jinsen.Flow visualization technique and its application in the study of fluid mechanics[J].Acta Aerodynamic Sinica, 1991, 9(2): 190-199.

Wind tunnel tests for aerodynamic interference between streamline type box bridges and rail vehicles under cross wind

ZOU Yunfeng1,2,3, HE Xuhui1,2, GUO Xiangrong1,2, HE Wei1,2, HE Jun1,2

(1.School of Civil Engineering, Central South University, Changsha 410075, China;2.National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China;3.China Construction Fifth Engineering Division CORP., LTD, Changsha 410004, China)

Existing studies showed that there is a significant aerodynamic interference between rail vehicles and bridges, however, most existing studies focus on streamline type high-speed rail vehicles and simply supported beam bridges with a blunt body shape, and the influence of bridge on aerodynamic forces of vehicle.Here, the aerodynamic interference between a streamline type box bridge and a rail vehicle with a blunt body shape was studied.The aerodynamic forces of the vehicle and the bridge for different combination cases and wind attack angles were measured in the wind tunnel laboratory of Central South University with a rigid section model force-measuring test, and a test platform was developed to ensure that the aerodynamic forces of the vehicle and the bridge can be measured synchronously.According to test results, the influences of aerodynamic interference between the vehicle and the bridge on the aerodynamic forces of the vehicle, the bridge and the vehicle-bridge system were analyzed.Furthermore, the aerodynamic interference mechanism was revealed according to the flow field visualization results which were obtained with the smoke-wire technique.The results laid a foundation for deriving empirical formulas to calculate the aerodynamic forces of vehicles and bridges considering their dynamic interference, and provided a reference for deeply understanding the aerodynamic interference mechanism between vehicles and bridges.

cross wind; streamline box bridge; rail vehicle; aerodynamic interference; vehicle-bridge system; wind tunnel test

国家自然科学基金(51322808; 51508580; U1534206)；湖南省自然科学基金(2016JJ3149)；中国博士后科学基金(2014M562133)；中国铁路总公司科技研究开发计划(2015G002-C)；中南大学“创新驱动计划”(2015CX006)；长沙理工大学桥梁工程安全控制省部共建教育部重点实验室开放基金(14KB02)

2015-10-30 修改稿收到日期：2016-01-27

邹云峰 男，讲师，博士,1984年生。

何旭辉 男，教授，博士生导师,1975年生。

U441+.2; U216 9

A

10.13465/j.cnki.jvs.2017.05.015