多平台对多目标无源融合定位方法

牟之英 ，刘 博

(1.中国航空无线电电子研究所，上海 200233；2.航空电子系统综合技术重点实验室，上海 200233)

多平台对多目标无源融合定位方法

牟之英1,2，刘 博1,2

(1.中国航空无线电电子研究所，上海 200233；2.航空电子系统综合技术重点实验室，上海 200233)

针对多目标环境下单平台和双平台无源定位系统无法消除大量虚假点难题，提出了一套基于三架飞机联合空间三角编队，并采用静态与动态相结合来滤除虚假点的多平台无源融合定位方法。该无源定位方式不需要飞机作机动，并能在多目标环境中快速有效地滤除虚假点，克服了单平台和双平台无源定位系统无法对多目标进行定位的缺陷，实现了系统全静默状态下同时对多个运动目标的融合定位与跟踪。给出了三平台无源组网对多目标融合定位与跟踪的实现结构、解算模型、误差分析以及虚假点滤除方法。仿真验证表明，该系统能实现对多运动目标的隐蔽探测、定位与跟踪，其跟踪精度能满足态势显示与火控攻击精度要求。

无源定位；多平台；多目标；虚假点滤除

0 引言

随着传感器性能的不断提高以及现代战争模式的日益复杂，如何提高飞机的作战能力同时又降低本机被敌机的截获概率一直是当今军事领域的研究热点。为提高生存能力，航电系统经常要工作在无源状态，此时仅能获得角度信息无法获取距离信息，因此无法对目标尤其是运动目标进行精确定位，通常需要探测器平台在空间作特殊的机动、多次测量来实现对目标的定位，或利用二个平台的角度探测信息对目标进行三角交叉定位解算，以求得目标的距离和运动参数[1-3]。

单平台无源定位系统要求平台的机动高于目标机动一个量级，即当目标做匀速运动时，观测平台至少作匀加速运动，这就限制了单平台无源定位系统的使用范围，通常它只能针对地面慢速运动的单目标进行定位。双平台无源定位系统对平台的运动没有特殊要求，但在多目标环境下，双平台无源定位系统会出现大量的虚假点，并由此产生伪航迹。研究发现，双平台无源定位系统出现的虚假点几乎无法消除，但通过增加平台数目可适当滤除虚假点，因此提出了多平台无源组网对多目标协同探测、融合定位与跟踪技术。但如何选择合适的平台数目、合适的平台布局以及合适的“鬼点”滤除方法才能有效消除虚假点并获得较高的定位精度一直是悬而未决的技术难题。虽然已有众多高校对多平台无源定位技术开展了理论研究和仿真试验，但仍无法解决多目标情况下三角定位解算产生的虚假点问题[4-5]。本文针对上述问题，提出了多平台对多目标无源融合定位方法。

1 多平台无源定位实现方法

1.1 多平台无源定位实现结构

1.1.1 平台数目选取

究竟采用多少平台才能有效消除虚假点，实现对运动多目标的精确定位呢，这是多平台无源定位系统首先要解决的问题。

如图1所示，对于空间存在N个目标，如采用两个测量平台，共有2N条方向线，存在N2个交叉点，其中有N(N-1)个交叉点是虚假点，所以对多目标而言需要更多的平台联合处理。如果考虑三个平台情况，如图2所示，则三条角度射线的交叉点只剩下四个，鬼点由6个变为1个，也就是其中的5个鬼点被剔除，随着组网平台数量的增多，鬼点剔除能力也会增大。

从定位精度而言，对于三平台乃至更多平台的组网探测而言，将存在2个乃至N-1个(N为平台的数量)的波门，如图3所示，这些波门的重叠区域可形成更精确的波门区域，而这个区域与双平台相比将大大减小，因此落在波门中的交叉点数量也将大大减小(但正确交叉点理论上不会被剔除)，多目标定位的精度也会大大提高。

综上所述，三平台是无源定位系统在多目标环境下的最小组网平台数。理论上随着组网平台数量的增多，定位性能将有所提高，但随之而来的解算复杂度也会大大增加，平台间的数据通信更为频繁，同步更为复杂，因此实际系统中平台数目不宜无限增大。

为了降低虚假点数目，提高目标定位精度，一个切实可行的方式为三平台联合空间三角布局，如图3所示，通过解耦的方式进行定性分析可知：其中两平台在同一水平面上通过方卫角的交叉定位可确定目标的水平距离；而垂直面上的平台可以与二个水平面上的平台通过俯仰角的交叉定位确定垂直距离，同时又形成一定约束，消除虚假交叉点。因此联合空间三角布局可以实现对空中运动目标较为精确的三维定位和跟踪。

1.1.2 实现结构

利用三个平台对多目标进行无源定位的实现框图如图4所示：当各个平台的传感器获得目标的测量信息后，首先独立完成各自的数据处理，形成目标方位和俯仰轨迹，送处理中心，处理中心将多个平台数据统一到一个公共坐标系下进行时间配准和空间配准，然后进行融合交叉定位解算。由于在多目标的情况下对于交叉定位解算出的定位点存在虚假点，我们采用静态与动态相结合的方法来去除虚假点，先计算定位点到各平台角度测量线的距离，根据距离进行粗判决，然后按距离最小原则对解算出来的定位点进行筛选，最后采用多假设跟踪方法，将定位点与已有航迹进行数据关联分析，动态地去除剩余的虚假点，同时建立航迹评分机制来对航迹进行起始、确认、删除与维持，最后通过跟踪滤波算法估计出目标的运动状态，并预测目标在下一时刻的位置以及跟踪波门。

1.2 多平台无源定位解算模型

多平台无源定位是利用多个观测平台得到的目标测向线在空间中必相交于一点(不考虑传感器测量误差情况下)，即目标位置点，所以只要有两条来自不同观测平台的测向线就可以进行交叉定位解算，求得目标的位置。

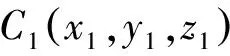
根据图中的几何关系，可得：对第i个观测平台有[6]：

(1)

(2)

由方程(1)、(2)可推出：

(3)

令

(4)

(5)

则：

Ai·X=Ki

(6)

A·X=K

(7)

若不存在误差，则通过方程组可求得目标的准确位置，但由于传感器测量误差以及平台自身定位误差的存在，两条测向线在空间形成异面直线，得不到目标的准确位置，但可以求方程组的最小二乘解作为目标位置的最佳估计值，其最小二乘解为[7]：

(8)

在几何意义上，最小二乘解即为到这两条定位线的距离和最小的点的位置。当i≥3时上式同样成立。

1.3 跟踪滤波算法

对目标的跟踪滤波方法有很多[8-9]，这里采用标准卡尔曼滤波，目标运动模型采用Singer模型[10]，即：

(9)

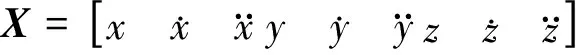
X(k+1)=Φ(k+1,k)X(k)+W(k)

(10)

其中

(11)

(12)

W(k)为状态噪声，其协方差矩阵为

(13)

式中，q11、q12…q33表达式参见文献[7]。

当αT≪1时，

(14)

Z(k)=HX(k)+V(k)

(15)

其中H为量测矩阵

(16)

V(k)为量测噪声，其协方差矩阵为：

(17)

其中，Ci、σi计算方法参考式(27)和式(39)。

用卡尔曼滤波算法即可得到目标运动状态的估计值和预测值。滤波估计算法参见文献[9]，在这里不再赘述。

1.4 定位误差分析

1.4.1 定位误差的解析模型

为了对式(1)得到的目标位置估计值的定位精度进行评估，我们计算其定位误差协方差矩阵如下[11]：

对第i个观测平台，由式(1)得：

(18)

则：

(19)

由式(2)得

(20)

(21)

其中，

(22)

(23)

令

(24)

(25)

(26)

(27)

(28)

则：

dVi=Ci·dX+Di·dXsi

(29)

对三个平台有：

dV=C·dX+D·dXs

(30)

其中，

(31)

(32)

(33)

(34)

则：

(dV-D·dXs)=B(dV-D·dXs)

(35)

式中，

(36)

因为各平台自身的定位误差与目标方位角、俯仰角的测量误差是不相关的，于是定位误差协方差矩阵可表示为：

BE[(dV-D·dXs)(dV-D·dXs)T]BT=

(37)

(38)

其中

(39)

由上式可以看出，定位误差主要来自两个方面：平台自身定位误差及传感器无源测向误差。另外，由于定位误差协方差矩阵中还包括了Ci项，而Ci中又包括了ri及di，这说明定位精度还与辐射源与各平台的相对位置有关。

1.4.2 影响定位误差的因素分析

式(38)给出了多平台无源融合定位误差的解析模型，它比较复杂，为了便于分析影响无源定位的诸多因素，可采用一种简化的模糊区分析方法。

如图6所示，由于测角误差的存在，两个平台对目标进行测向交叉定位存在一定的模糊区，如图阴影部分[12]。

当二个平台的测角误差相等时，其面积可近似用下式计算：

(40)

因此，多平台定位模糊区与基线长度L，传感器测角误差方差σ、两个无源观测站所测得的方位角θ1和θ2以及交会角β有关。

定义定位精度的几何稀释为[13]：

(41)

如果忽略载机自身的定位误差，且考虑而平台测角误差相互独立，则二维情况下GDOP=S，它描述了定位误差的几何分布图。

图7根据式(41)给出了双平台无源定位误差分布示意图。

由图7可看出：

1)当目标在基线上，定位误差较大；

2)当目标在基线的延长线上，无法进行无源定位；

3)一般情况下，目标离平台越远，定位误差越大；

4)最好保证两平台与目标之间的距离基本相等。

可以证明，当θ1=±35.27°，θ2=±144.73°时的GDOP最小。两角度之差为交会角，因此得到最优交会角近似为110°，当目标与观测平台的相对位置关系满足此条件时，对目标的状态估计精度最高。

2 多目标环境下的虚假点剔除方法

2.1 静态去除虚假点方法

针对上节解算出的所有交叉定位点，首先计算其到相应三个平台的角度测量线的距离，若距离不满足门限，则将其作为虚假点去除，对距离满足门限的所有点，求出它到三个平台的角度测量线的距离之和，并对距离之和进行排序，根据可能的目标数目n(n可设为各平台测量得到的目标数之和)，选出距离之和最小的n个定位点作为可能的目标位置。

门限定义如下：

Ri≤k×ri×σi

(42)

(43)

(44)

2.2 动态去除虚假点方法

静态去除虚假点方法不能把所有虚假点滤除干净，对于保留下来的虚假点则可利用数据关联方法进行动态滤除。这是因为在连续多拍中，“虚假点”往往不符合目标运动规律，难以形成稳定航迹，随着时间推移，对“虚假点”的跟踪就会发散，而对应于真实目标点跟踪会收敛形成航迹，从而实现“虚假点”的动态滤除。

为有效去除虚假点，并节约计算量，我们采用简化的多假设跟踪算法(MHT)进行数据关联，它借鉴了MHT的多假设跟踪思想[9]，但简化了航迹假设过程和航迹输出逻辑，取消了回溯过程及其带来的判决延迟，易于工程实现。其实现步骤如下：

1)为各条航迹生成预测波门，将静态去鬼点后留下的交叉点作为目标检测点与航迹关联，即计算交叉点与航迹预测位置的归一化统计距离dij：

(45)

当dij

(46)

其中，PD为检测概率，βFA为虚警概率，βN为真实目标概率，d和S意义同前。

2)删除得分较低的关联对，可以得到如图8关联类型。其中上面一排为测向交叉点，即目标检测点，下面一排为各种目标航迹(临时航迹、虚拟航迹、确定航迹)。

3)解关联和航迹分支

①如果一个检测只与一条航迹关联(如类型1)，则关联结果很明确。

②如果几个检测都与一条航迹关联(如类型2)，则对航迹进行分支，选关联得分最高的那条分支作为确定航迹，其他作为虚拟航迹。

③如果几条航迹都与一个检测关联(如类型3)，则判断这些航迹是否需要合并，判断依据如下：

判断两条航迹的最后K帧的航迹状态估计值之间的距离是否小于一定的门限，即如果

(Xn(k)-Xm(k))≤N

(47)

对不能合并的航迹，则检测将用于更新关联得分最高的那条航迹

④对类型4和5这种复杂的关联关系，首先判断哪些航迹需要合并，然后计算检测点与航迹的最佳分配策略，最佳分配结果应符合下面约束条件：

•每个交叉点只与一条航迹关联；

•所有关联对得分之和最高。

4)根据关联分配结果，更新航迹，并计算航迹得分。

航迹更新采用标准卡尔曼滤波方法(在第5节中描述)，航迹得分计算方法如下：

LLR(k)=LLR(k-1)+ΔLLR(k)

(48)

(49)

其中，P0(T)是航迹为真实目标的先验概率，可由空间中的虚警概率βFA和真实目标概率βN得到。

①对分配到检测点迹的航迹，将检测点迹用作观测数据，利用卡尔曼滤波方法对目标运动状态进行估计，此时

(50)

②对没有分配到检测点迹的航迹，用卡尔曼预测方法对目标运动状态进行外推，此时

(51)

③对合并后的航迹得分进行修正，

Ls=Ls+ln[1+e-(Ls-Ld)]

(52)

其中，Ls为保留下的航迹的分数，Ld为删除航迹的分数。

④对分支生成的虚拟航迹得分赋初值，即航迹分数为

(53)

5)根据航迹得分判断哪些航迹需要升级(由虚拟航迹或临时航迹为确定航迹)，哪些航迹需要保留、哪些航迹需要删除。

通常定义两个门限：航迹删除门限TL和航迹确认门限TU。

如果LLR

如果TL

如果TU

航迹删除门限TL和确认门限TU的计算方法为：

(54)

(55)

其中，α为虚假航迹被确认的概率，即伪航迹生成概率，β为真实航迹被删除的概率，即漏检概率。

6)航迹起始。

①利用上述方法将没有与任何航迹关联上的检测点与上一帧孤立点进行关联判决和航迹评分，如果TL

②将没有与任何航迹关联上的检测点迹作为孤立点迹放入航迹文件，用于下一帧航迹起始。

7)对所有新生成的临时航迹、虚拟航迹进行航迹编号，并输出所有确定航迹。

3 仿真结果分析

我们针对三个平台对四个目标的无源定位过程进行了仿真。仿真场景为：

图9给出了对4个目标的跟踪曲线，其中直线为真实目标运动轨迹，曲线为跟踪曲线。图10、11分别给出了目标1和目标3的综合位置误差曲线，其中横轴为帧号(1帧=250ms)，纵轴为根据式(57)计算出来的综合位置误差(RMSE)，上面一根曲线为测向交叉定位解算结果，下面一根曲线为卡尔曼跟踪滤波结果。

综合位置误差计算方法如下：

(58)

图12给出了经过100次门特卡罗仿真的统计结果，其中纵轴为综合位置误差与距离的比值，横轴为目标相对于无源定位解算平台的距离，上面一根曲线为多平台交叉定位解算误差曲线，下面一根曲线为跟踪滤波误差曲线。

由图10、图11可以看出，位置误差基本上稳定在100～200m，由图12可以看出，多平台无源融合定位误差随目标的接近而减小，经过大量的测试和统计分析可以得到以下结论：当平台测角误差为5mrad时，定位精度可达1% R左右，当平台测角误差为20mrad时，定位精度一般可达3% R左右，当目标距离小于80km时，稳态滤波定位误差<0.5% R，此时多平台无源融合定位结果可用于火控攻击。

为验证虚假点去除概率，我们设置了9个机动运动与6个匀速直线运动混合目标，见图13,包含平行飞行和交叉目标，图14给出了鬼点去除概率(纵轴为鬼点去除概率，横轴为帧号，1帧=40ms)，其中下面一根曲线是静态去鬼点概率，上面一根曲线是静态与动态相结合的去鬼点概率，可以看出静态去鬼点概率可达80%，静态与动态相结合的鬼点去除概率可达90%以上。

4 结论

本文提出了多平台对多目标无源融合定位方法。该方法不需要飞机作机动，并能在多目标环境中快速有效地滤除虚假点，克服了单平台和双平台无源定位系统无法对多目标进行定位的缺陷，实现了系统全静默状态下同时对多个运动目标的融合定位与跟踪。仿真验证表明，在测角误差为5 mrad(编队IRST组网)情况下，多平台无源定位精度可达1%R，当目标距离小于80 km时，稳态滤波定位误差<0.5%R，此时多平台无源定位系统可用于火控攻击；在测角误差为1°(编队ESM组网)情况下，稳态滤波定位误差<3%R，此时多平台无源定位系统可用于态势感知。

[1]孙仲康，周一宇，何黎星. 单多基地有源无源定位技术[M]. 北京：国防工业出版社，1996.

[2]胡来招. 无源定位[M]. 北京：国防工业出版社, 2004.

[3]万方，丁建红，郁春来. 利用空频域信息的固定单站无源探测定位方法[J]. 探测与控制学报，2010，32(3)：91-95.

[4]王本才， 王国宏， 何友. 多站纯方位无源定位算法研究进展[J]. 电光与控制，2012，19(5)：56-62.

[5]单月晖，孙仲康，皇甫堪. 不断发展的无源定位技术[J]. 航天电子对抗，2002(1)：36-42.

[6]陈玲，李少洪. 无源测向测时差定位算法研究[J]. 电子与信息学报，2003，25(6)：771-776.

[7]Yu Huagang，Huang Gaoming，Gao Jun, et al. Practical constrained least-square algorithm for moving source location using TDOA and FDOA measurements[J]. Journal of Systems Engineering and Electronics， 2012，23(4)：488-494.

[8]Wu Jianmin，Mou Zhiying，Zhu Qiang, et al. Decoupled target tracking with bearingsonly measurements[J]. Optical Engineering December, 2012，51(12).

[9]何友，王国宏，关欣，等. 信息融合理论及应用[M]. 北京：电子工业出版社，2010.

[10]Masamichi Kojima. A study of Target Tracking Using Track-oriented Multiple Hypothesis Tracking[J]. SICE，1998(5)：29-31.

[11]修建娟. 多站无源定位与跟踪算法研究[D]. 烟台:海军航空工程学院，2004.

[12]李洪梅，陈培龙. 三维多站测向交叉定位算法及精度分析[J]. 指挥控制与仿真，2007，29(2)：54-59.

[13]贾兴江. 周一宇运动多站无源定位关键技术研究[D]. 长沙：国防科技大学，2011.

Research on Multi-platform Passive Location for Multi Targets

MOU Zhiying1,2, LIU Bo1,2

(1.China National Aeronautical Radio Electronics Research Institute, Shanghai 200233, China; 2.Science and Technology on Avionics Integration Laboratory, Shanghai 200233, China)

In order to solve the problem that a lot of false intersection points appear in the passive location system based on one or two platforms in multi-target environment, a new passive location system based on three platforms is put forward in this paper, which forms triangular formation in space and removes false intersection points by combining static manner with dynamic one. This system doesn’t need the airplanes to maneuver, and is able to remove the false points fast and effectively. It overcomes the defect that the passive location system based on one or two platforms is unable to locate multi-targets, and realizes the function that several moving targets are located and tracked simultaneously in a full silent state. The implemention structure, specific model algorithm, error analysis and the way of removing false intersection points are given in detail. The simulation results demonstrate that the system is able to detect, position and track multi-targets silently, and the accuracy of track can meet the requirements of the situation display and attacking.

passive location; multi-platform; multi targets; false points removing

2016-07-02

总装基金项目资助(项目编号不公开)

牟之英(1961—)，女，上海人，硕士，主任研究员，研究方向：信息融合与传感器管理。E-mail:mouzhiying@aliyun.com。

TP391

A

1008-1194(2017)01-0058-08