细丝微细磨削中的轮廓成形研究

黎 桥 朱援祥 周立武 周 兵.武汉大学动力与机械学院，武汉，43007.中国三峡集团建设管理公司工程检测中心，宜昌，44333

细丝微细磨削中的轮廓成形研究

黎 桥1朱援祥1周立武1周 兵2
1.武汉大学动力与机械学院，武汉，4300722.中国三峡集团建设管理公司工程检测中心，宜昌，443133

为实现细丝局部微加工，提出了一种新的细丝磨削方式。对磨削过程细丝弯曲进行受力分析，导出了磨具对细丝的顶压力计算公式，并分别建立了磨具与细丝接触区内的压力分布和磨粒切削深度分布模型；根据磨削位置与顶压力的关系，提出挠度调整方式来实现阶梯丝和锥度丝的磨削。在自制的磨削设备上，用机器视觉作为测量方法，进行细丝定点磨削和扫动磨削实验。定点磨削实验表明，细丝磨削后的轮廓为抛物线，其轮廓变化规律表明，磨削初期，接触区内压力呈抛物线分布，之后逐渐趋于均匀分布，而细丝挠度对材料去除率和抛物线形状起决定作用。扫动磨削实验表明，控制挠度调整的参数，设备可加工圆滑过渡的阶梯丝和锥度丝。

细丝微磨削；接触压力；视觉测量；轮廓成形

0 引言

在介入医疗中，细丝常用作血管中的导向工具和柔性导丝中的金属硬芯[1]，这对细丝局部形状提出了不同的要求。其中，细丝端部常被加工出一定锥度，以减小金属丝对人体组织的伤害[2]。这种锥度丝目前采用传统的磨床进行磨削加工，但由于在刚性垫板上磨削时，细丝受力较大，因此磨削后细丝表面质量较差，而且细丝磨削后的形状也无法准确控制。

目前为止，关于细丝局部加工方面的研究报道还较少。WANG等[3]采用柔性约束方式实现细丝端部斜面的加工，并研究了工艺参数对细丝弯曲变形量、表面粗糙度和磨削力的影响。

为实现锥度丝和阶梯丝的加工，本文提出一种新的柔性约束下的磨削方法，并研制了相应的磨削设备。在此磨削设备上，对细丝在磨削时的轮廓成形过程、磨具与细丝接触区的压力分布和锥度丝磨削成形工艺进行了研究。

1 细丝磨削基本原理

如图1所示，细丝两端被弹簧拉紧，中部被支撑，处于悬空状态。圆棒状磨具向下顶压细丝，使之产生一定弯曲变形，然后磨具和细丝各自转动，实施磨削。

细丝磨削分两种基本方式：定点磨削和扫动磨削。两种磨削方式中，细丝都以一定速度转动。定点磨削时，磨具只在其轴线方向(y方向)做往复运动，以使自身磨损均匀。而扫动磨削时，除上述运动外，磨具还沿细丝轴线方向(x方向)做往复运动，以加工一定区间。

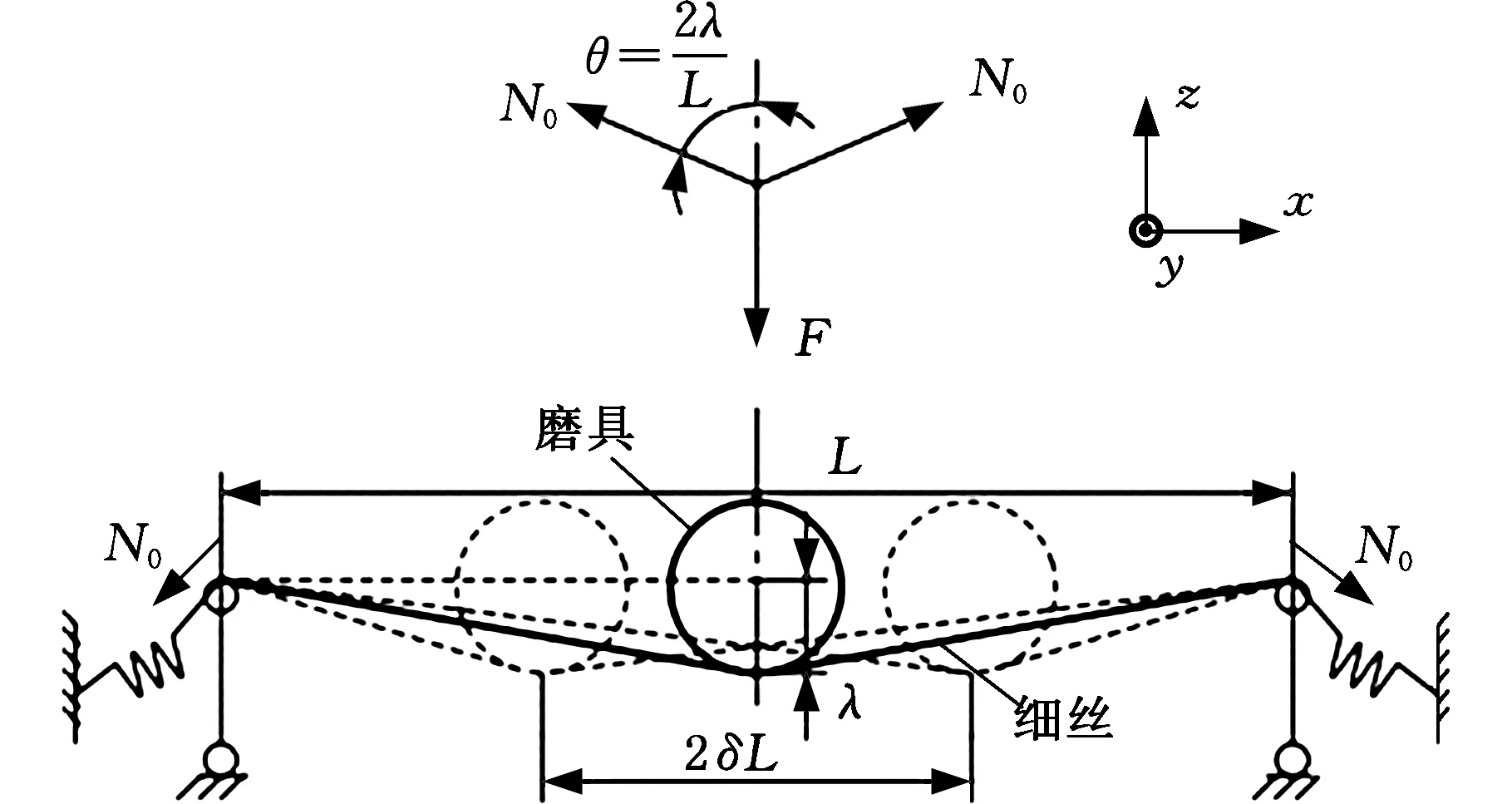
图1 细丝磨削模型Fig.1 Schematic of wire grinding

1.1 磨具对细丝的顶压力

由图1中受力情况可知，当磨具位于支撑段中点时，两端张力与顶压力F平衡，则有

(1)

式中，λ为细丝变形挠度;N0为弹簧张力;L为支撑长度。

当磨具偏离支撑中点时，F的大小和方向同时发生改变，在λ≪L时，F水平分力远小于竖直分力，可忽略。设磨具与支撑中点的距离为δL(-0.5 <δ< 0.5)，则此时顶压力F为

(2)

1.2 接触区内的压力分布

HERTZ给出了小应变条件下弹性体接触区的压力分布。但在本文所述的情况下，细丝刚度小，与磨具的接触区很大，不满足Hertz的弹性半空间假设。尽管如此，由于细丝和磨具表面均为二次曲面，因此Hertz对接触区为椭圆的假设仍然适用。JOHNSON[4]给出了接触区压力分布的一般情况：

(3)

其中,p为单位面积上的压力;p0为接触区中心压力；a、b为接触椭圆的长短轴；x为细丝不变形时的轴线方向，y为磨具轴线方向，原点在接触区中心。n值决定压力分布类型，n=0.5时为Hertz压力。JOHNSON指出：如果接触区内物体具有连续的外形，则压力将从中心均匀地降到边界上的零值，因此n>0，而具体值将由实验测出。

在接触椭圆内对式(3)积分得到总压力，其值等于顶压力F，据此算出接触区中心的压力为

(4)

当挠度λ增大时，顶压力F线性增大，接触区有所扩大。尽管如此，总压力增大时，接触区中心压力p0增大。

1.3 磨粒切削深度

为简化模型，假定磨粒在磨具表面均匀排布，切削深度只取决于其所受压力，而压力值由式(3)给出。XU等[5]从力学角度研究了作用在单颗磨粒上的压力与其切除的体积之间的关系，并认为磨粒单位长度切除的体积(即切屑的横截面积)正比于压力的平方：

(5)

式中，A为常数；Ew为工件的弹性模量；pg为作用在磨粒上的压力；HV为维氏硬度；KIC为断裂韧度。

根据文献[5]的结论，可以推知磨粒的切削深度与其所受压力成正比，即

tm=Kpg

(6)

其中，常数K与磨粒分布、几何形状、磨具和细丝的运动速度等参数有关。

综合式(1)、式(3)～式(5)，接触区内所有磨粒每次切去的总体积为

(7)

1.4 细丝扫动磨削中的调整

扫动磨削过程中，由于加工位置变化，顶压力F也随之变化。当磨具处于细丝支撑中点时，F最小，造成细丝中部的磨削量小，出现凸点。

根据式(2)，可在磨具扫动过程中同步地调整挠度，以主动控制F的大小。设支撑中点的挠度为λ0，则当磨具与中点偏距为δL时，有如下调整公式：

λ=(λ0-k1Lδ2)(1-k2|δ|)

(8)

其中，k1、k2为调整系数。当k1=4λ0/L时，将式(8)代入式(2)中，可得

(9)

按式(9)进行调整时，扫动过程中F将随着δ线性变化，则由式(6)可知，磨粒切削深度也将线性变化，最终可加工出一定锥度的细丝；特别地，当k2=0时，加工出圆滑过渡的阶梯丝。

2 磨削实验

图2所示为自行研制的细丝磨削设备，磨具安装在三轴数控工作台上，实现三方向运动，运动控制系统可控制磨具按预定路径运动。磨具旋转由伺服电机带动，细丝旋转由步进电机带动。

图2 细丝磨削设备Fig.2 Full view of wire grinding device

本设备采用视觉测量作为测量方法，细丝加工部位经过体视显微镜45倍光学放大，再用500万像素的CCD相机采集图像，经标定，细丝图像的1个像素对应的实际尺寸为1.49 μm。

视觉测量系统可对细丝轮廓进行提取，并测量出细丝直径；结合运动控制系统，视觉测量系统可测出细丝的三维形貌。图3所示为CCD采集的细丝图像及其三维形貌。

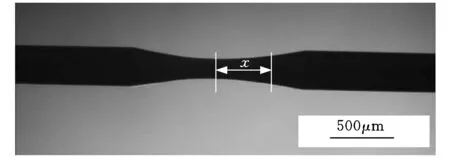
(a)细丝轮廓

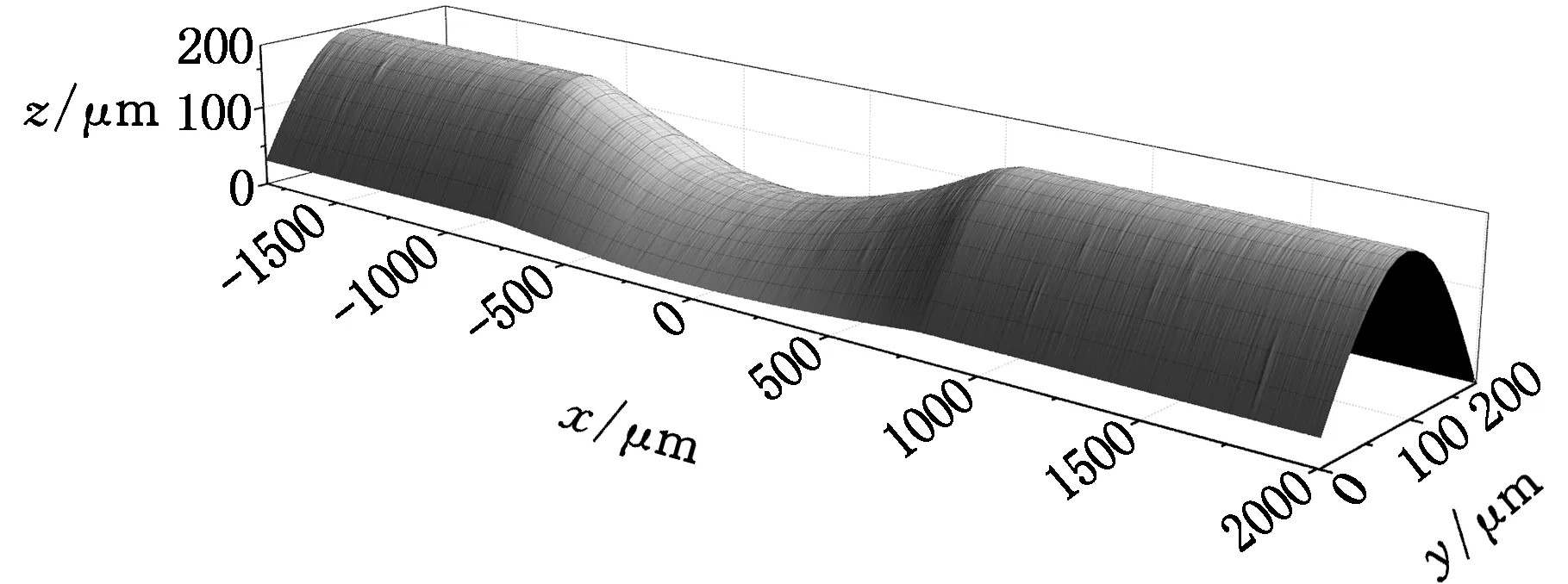
(b)三维形貌图3 细丝图像Fig.3 Wire image

用视觉测量系统对细丝转动过程的振动情况进行了测量，测量频率为5.8 Hz。如图4所示，细丝在不同转速nw下的振动幅度均不超过为12 μm，频率与细丝转动频率相同。为减小细丝振动的影响，磨削时的细丝挠度不宜过小。

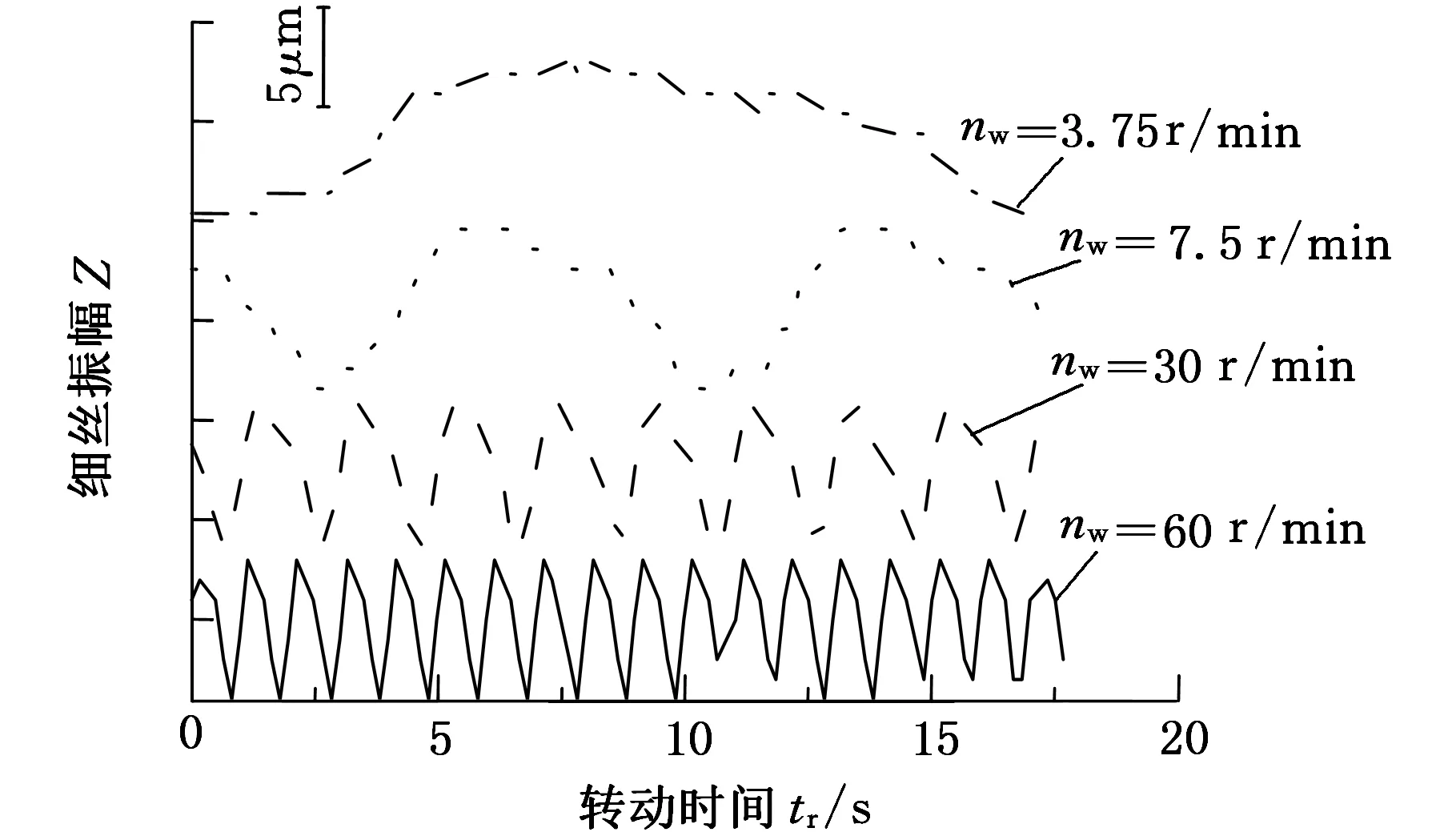
图4 不同转速下的细丝振动Fig.4 Vibrations of wire at various rotating speed

在磨削设备上，进行了细丝定点磨削和扫动磨削实验，磨削过程的基本参数见表1。

表1 磨削实验参数
Tab.1 Parameters of grinding experiments

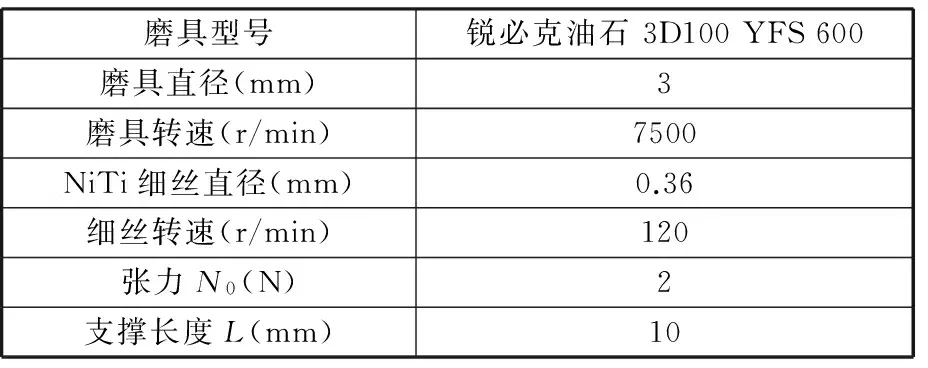
磨具型号锐必克油石3D100YFS600磨具直径(mm)3磨具转速(r/min)7500NiTi细丝直径(mm)0.36细丝转速(r/min)120张力N0(N)2支撑长度L(mm)10

在λ为100 μm、150 μm、200 μm时进行定点磨削实验，磨削时间为70 s，每隔10 s用视觉系统测量一次细丝轮廓(直径沿细丝轴线的分布)，并计算磨削区宽度和去除的体积。

用式(9)中的挠度调整方法，对细丝进行扫动磨削。其中，λ0=200 μm，磨具扫动速度为2.5 mm/s。分别在无挠度调整、k2为0、 5、 10的挠度调整下进行磨削，时间分别为100 s、200 s、150 s、150 s，磨具扫动宽度分别为1200 μm、1500 μm、1200 μm、1200 μm。磨削完成后，用视觉系统测量细丝轮廓，并对磨削后的细丝横截面进行制样，用光学显微镜拍摄细丝截面。

3 实验结果

3.1 定点磨削的实验结果

图5a～图5c分别为λ为100 μm、150 μm、200 μm时，细丝在定点磨削过程中不同时刻的轮廓，轮廓的局部波动由细丝表面的磨屑造成。用相邻时刻的轮廓作差，得到该时段内的磨削量分布，图5d为200 μm下不同时段的磨削量分布。

由图5a～图5c可知，细丝磨削区轮廓具有对称性，磨削区中心直径最小，经70 s磨削后，挠度为100 μm、150 μm、200 μm的细丝最小直径分别为282 μm、202 μm、173 μm。由图5d可知，当挠度为200 μm时，在0～10 s内，中心磨削量最大，且磨削量关于中心对称，随后磨削量越来越小，且分布基本均匀。λ为100 μm、150 μm时磨削量变化规律相同。

图6为不同挠度下磨削区宽度随时间变化的曲线。由图可知，磨削区宽度在磨削过程中增加，磨削后期，磨削区宽度变化较缓慢，而在λ=100 μm，磨削60 s后，磨削区宽度趋于稳定。对图中曲线进行外延，可得0时刻的磨削宽度，也即磨削与细丝接触区的长度，图中3条曲线外延结果分别为349.85 μm、493.56 μm、562.91 μm。

图7为不同挠度下材料去除率随时间变化的曲线，图中的材料去除率是由10 s内的去除体积计算而来，表征这10 s内的平均材料去除率。由图可知，材料去除率与λ基本成正相关，随着磨削的进行，材料去除率呈减小趋势，原因有：①磨具与细丝的接触区扩大；②细丝直径减小导致λ减小，从而顶压力F减小。这两个原因都将导致接触区单位面积上的压力减小，使磨粒切削深度减小，从而使材料去除率减小。

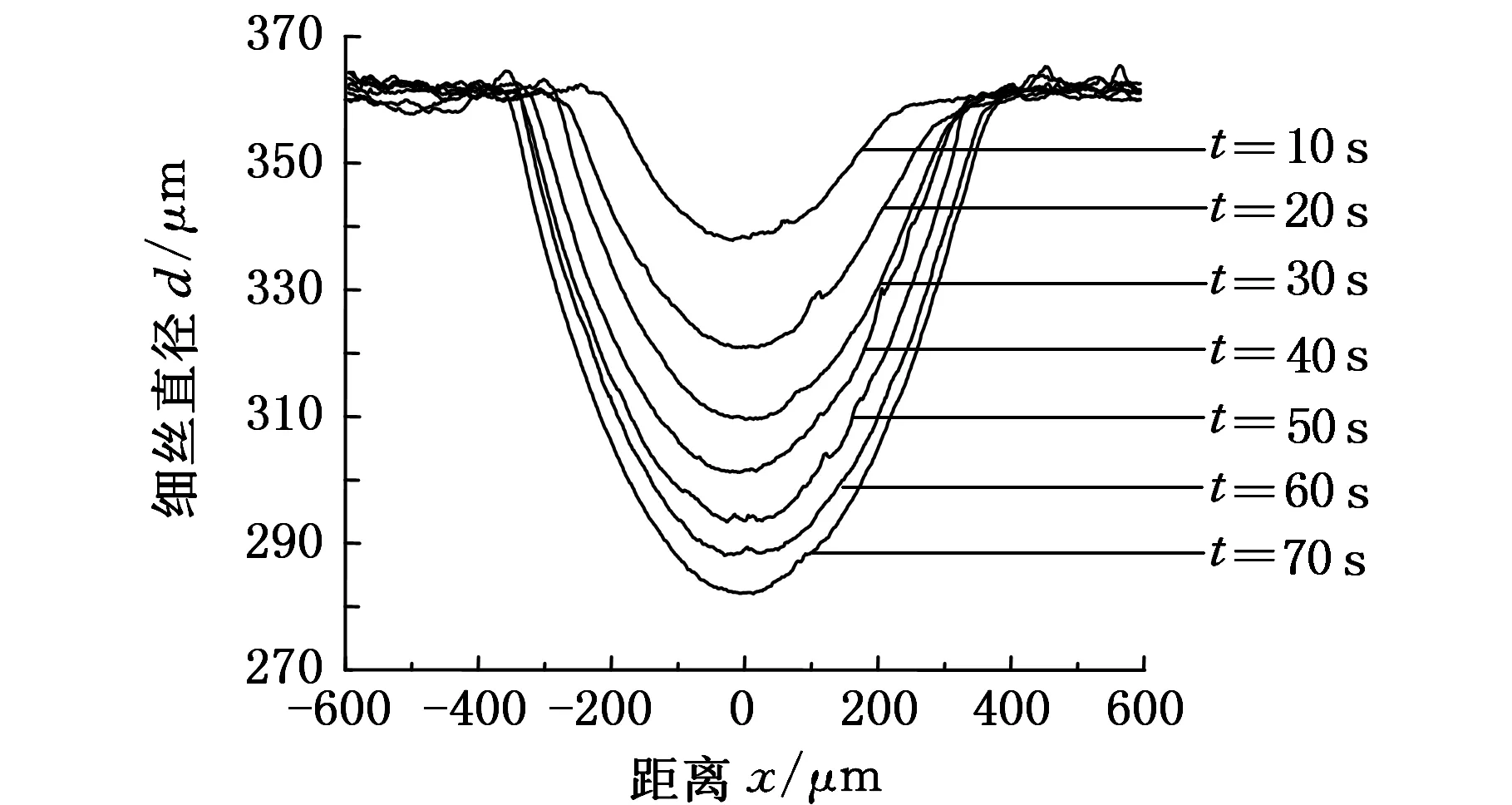
(a)λ=100 μm的细丝轮廓

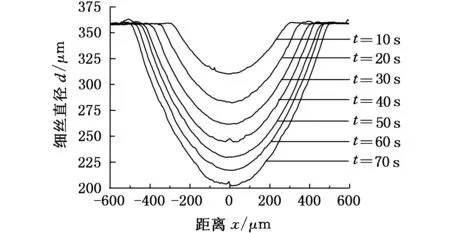
(b) λ=150 μm的细丝轮廓

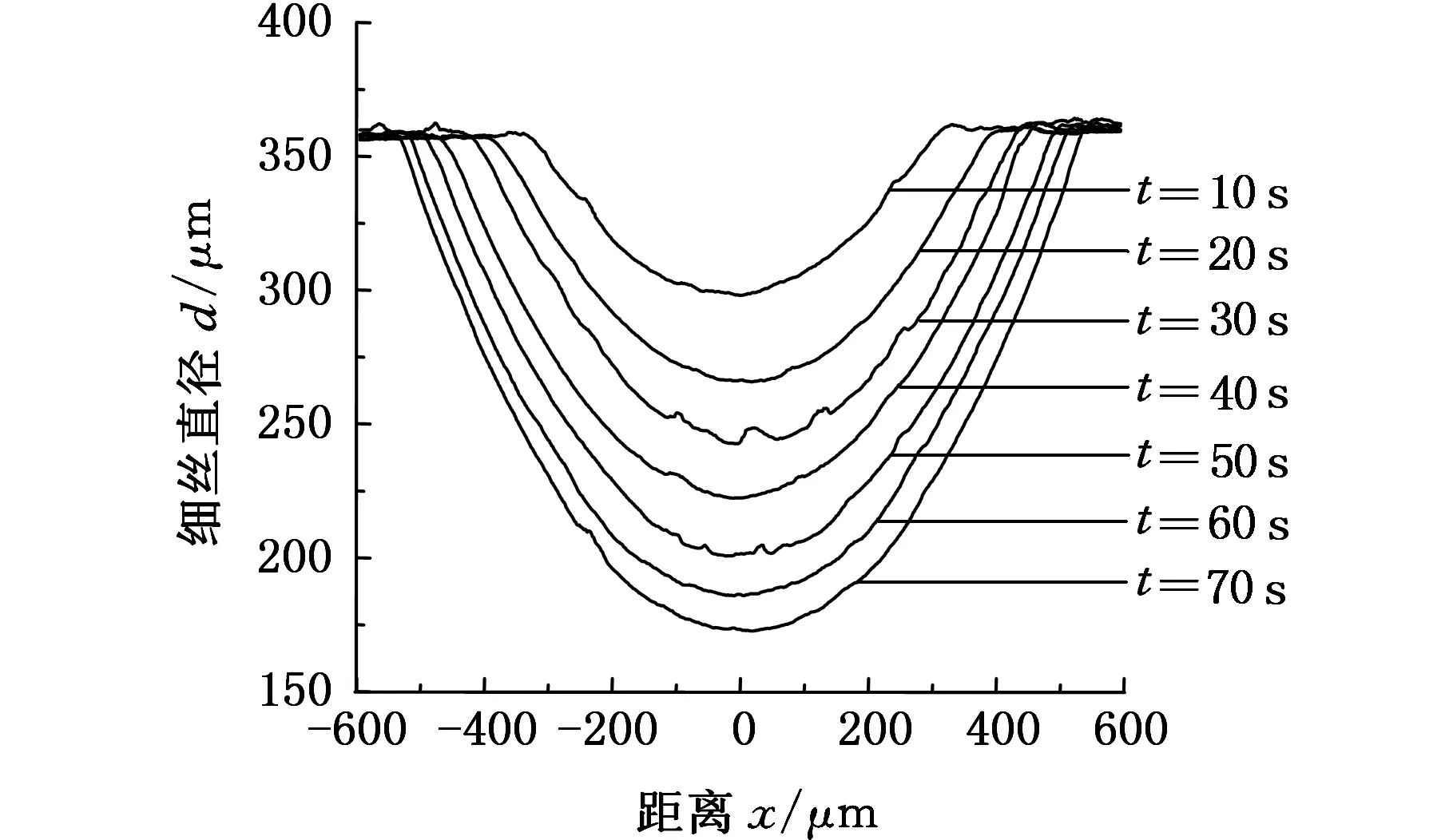
(c)λ=200 μm的细丝轮廓

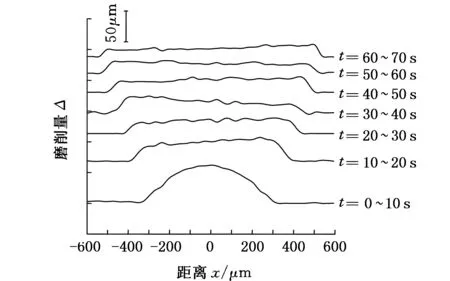
(d)λ=200 μm的磨削量图5 定点磨削中细丝轮廓及磨削量的变化Fig.5 Outline evolution of wire in fixed-position grinding and the grinding depth evolution

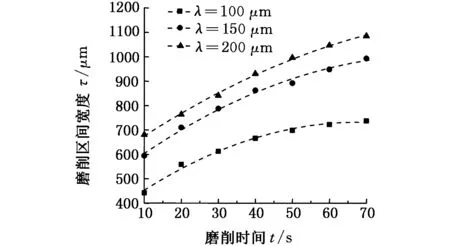
图6 定点磨削过程磨削宽度变化Fig.6 Evolution of the grinding width in fixed-position grinding

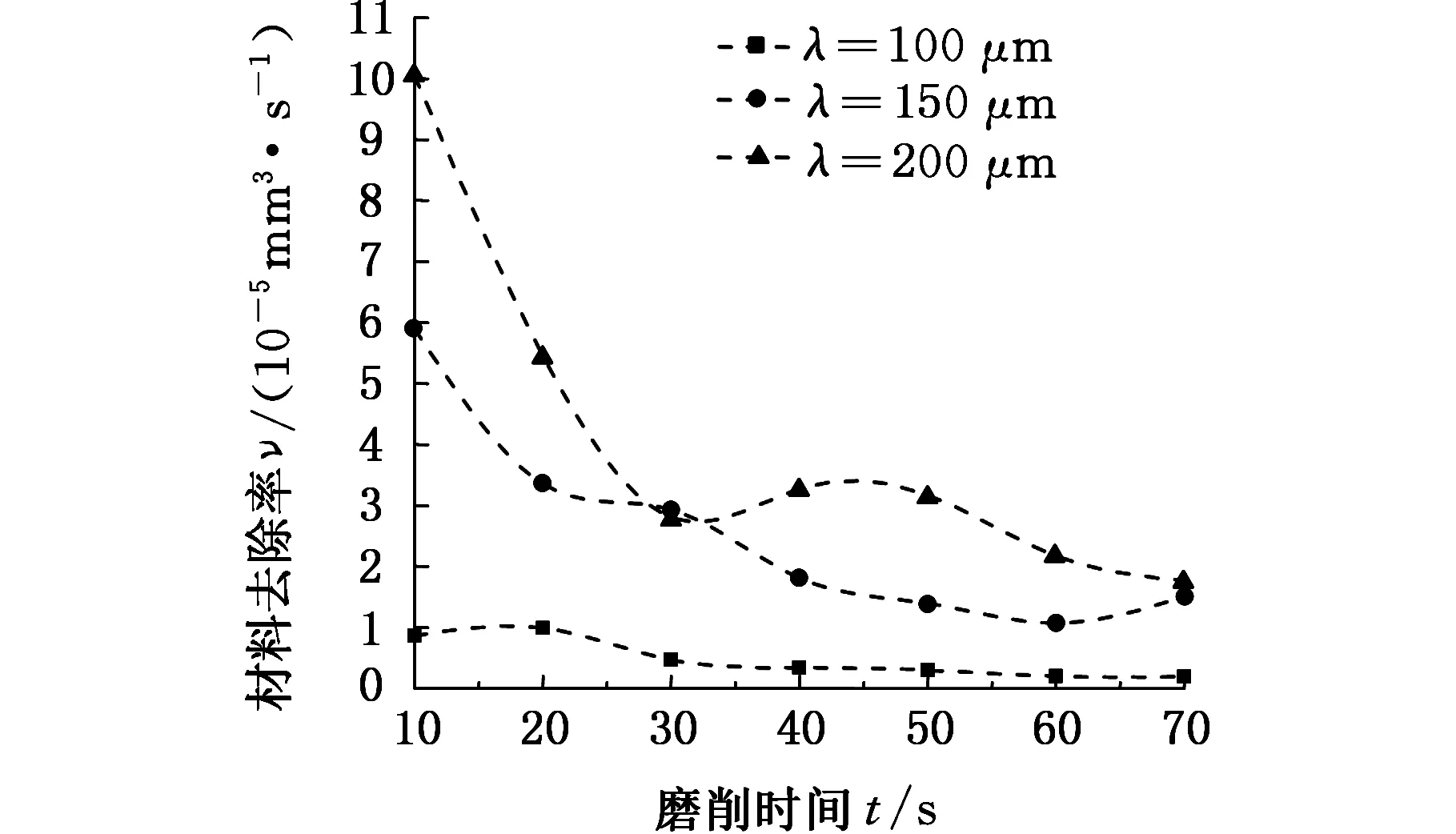
图7 定点磨削过程材料去除率变化Fig.7 Evolution of material removal rate in fixed-position grinding

同时，由图7可知，挠度越大，材料去除率越大，这与式(7)给出的规律一致。需说明的是，图中150 μm和200 μm对应的曲线在30 s处出现交点，这是由于细丝表面的磨屑和灰尘造成的计算误差(可参看图5c中30 s时的细丝轮廓)。

3.2 扫动磨削实验的实验结果

图8所示为磨削后的细丝轮廓。由图8可知，由于没有调整挠度，图8a中的细丝在磨削后，磨削区中间有局部凸点。而k2为0的调整方式下，加工出了圆滑过渡的阶梯丝，中部有一宽度约600 μm的平直段。在k2为5、10的调整方式下，加工出带锥度的细丝，角度分别为9.6°和14.1°。

由图9可知，细丝圆整度没有因磨削而变差，表明细丝周向磨削很均匀。

4 讨论

4.1 细丝定点磨削过程的分析

对70 s时的细丝磨削区轮廓进行抛物线拟合，表2列出了拟合结果，拟合残差代表拟合曲线与实际数据的平均偏差。由表中的残差可知，磨削区内轮廓与抛物线具有很高的重合度，可以认为磨削区轮廓为抛物线。

(a)无挠度调整

(b)k2=0

(c)k2=5

(d)k2=10图8 扫动磨削形成的细丝轮廓Fig.8 Outline of the wire manufactured by sweeping grinding

(a)细丝原始截面 (b)磨削区中部的截面图9 细丝横截面Fig.9 Cross-section of the wire

表2 细丝轮廓抛物线拟合Tab.2 Parabolic fitting results of wire outline

根据图5d给出的磨削量分布的演变过程，可知在定点磨削的0～10 s内，磨削量呈抛物线分布，中心的磨削量最大，由图7可知这个阶段的材料去除率是最大的，因此细丝轮廓由原始的直线迅速变为抛物线，由表2可知，λ的大小决定了抛物线的形状。磨削时间超过10 s后，磨削量分布逐渐均匀，切口形状基本不发生变化，此阶段的磨削，磨具只是将参数已定的抛物线切口向材料内部平移。

4.2 细丝与磨具接触区的压力分布

细丝与磨具的实际接触区比磨削区要大，但二者很接近，因此本文对二者不加区分。

图5d给出的磨削量是接触区内所有磨具共同切削10 s的总结果，反映了磨粒单次切削的深度。由式(6)知，磨粒切削深度的分布正比于压力分布，由图5d可知，在磨削0～10 s内，接触区内压力分布是抛物线型的，即式(3)中的n值为1。

JOHNSON[4]指出，抛物线分布的压力是在具有二次曲面外形的刚性物体法向顶压弹性基垫过程中产生的。事实上，细丝两端由弹簧张紧，加上细丝自身的抗侧刚度很小，因此在磨具顶压过程中，细丝可看成Winkler弹性基，因而出现抛物线型的压力分布。

由图5d可知，磨削过程中，接触区压力逐渐由抛物线分布转向均匀分布。

4.3 与传统刚性约束下的磨削对比

传统磨削中，工件固定在磨床上，约束是刚性的。每次进给过程中，磨具将一定进给厚度的材料全部切除，因而单次加工量由进给量决定。由于磨具与工件之间作用力较大，容易出现工件烧伤、磨具磨损严重等现象。同时，磨削后工件表面出现回弹，降低了加工精度。

相比之下，本文提出的细丝磨削方式不存在上述问题。由于细丝有足够的柔性，受磨削顶压后，其弹性应变量相比传统刚性约束下的应变量小很多，因此回弹量也较小。而材料去除率由挠度控制，磨削量(直径减小量)由磨削时间控制。通过挠度与时间的配合，可对细丝磨削后的直径进行精确控制。因此，本文所用的磨削方式更适用于细丝局部微加工。

5 结论

(1)定点磨削过程中，在0～10 s内，磨削区的细丝轮廓由直线迅速变成抛物线。之后的磨削过程中，切口形状基本不变，磨具只是将参数已定的抛物线切口向材料内部平移。

(2)从磨削量分布的演变规律可得，在磨削初始阶段，接触区压力呈抛物线分布，接触区中心的压力最大，随后压力趋于均匀分布。

(3)用不同的挠度调整方式对细丝进行扫动磨削。实验结果表明，通过控制挠度调整方式，本设备可加工圆滑过渡的阶梯丝和带锥度的丝，且磨削后细丝截面依然圆整。

[1] 赵军辉，张志清. 临床介入治疗器材及材料的结构与性能简介[J]. 中国医疗设备，2009，24(2)：54-57. ZHAO Junhui, ZHANG Zhiqing. Structure and Performance of Interventional Therapy Material [J]. China Medical Devices, 2009, 24(2):54-57.

[2] HEAVNER J E, RACZ G B, JENIQIRI B, et al. Sharp Versus Blunt Needle: a Comparative Study of Penetration of Internal Structures and Bleeding in Dogs[J]. Pain Practice ,2003,3(3):226-231.

[3] WANG Y, TAI B L, LOON M V, et al. Grinding the Sharp Tip in Thin NiTi and Stainless Steel Wires[J]. International Journal of Machine Tools & Manufacture, 2012, 62(1):53-60.

[4] JOHNSON K L. Contact Mechanics[M]. Cambri-dge: Cambridge University Press, 1985：84-144.

[5] XU H H K, JAHANMIR S, IVES L K. Mechanisms of Material Removal in Abrasive Machining of Cera-mics[J]. Interceram International Ceramic Review, 1998, 47(6):380-385.

(编辑 王旻玥)

Study on Contour Shaping in Wire Micro-grinding

LI Qiao1ZHU Yuanxiang1ZHOU Liwu1ZHOU Bing2

1.School of Power and Mechanical Engineering,Wuhan University, Wuhan, 430072 2.Engineering Detecting Center, Construction and Management Company of Yangtze Three Gorges Group, Yichang, Hubei, 443133

In order to realize the micro-machining on local area of wires, a new grinding method was proposed. Through the force condition analysis of the deflected wires, the jacking force formula was deduced. The pressure distribution in contact area and cutting depth distribution of the grains were modeled respectively. Based on the relationship between the grinding positions and the jacking forces, a deflection adjusting method was proposed to realize the grinding processes of step wires and taper wires. In a self-assembled grinding platform, machine visual was taken as measurement method, fixed-position grinding and sweeping grinding experiments were conducted. The results of fixed-position grinding show that the wire profile in grinding area is parabolic after grinding. Shape evolution of wires suggests that the pressure distribution on contact area is parabolic initially and tends to be uniformed as the grinding goes on. The wire deflection has a critical impact on the material removal rate and the shape of the parabola. The results of the sweeping grinding show that step and taper wires may be obtained with different deflection adjusting parameters.

wire micro-grinding; contact pressure; visual measurement;Contour shaping

2016-01-13

TG74

10.3969/j.issn.1004-132X.2017.01.006

黎 桥，男，1992年生。武汉大学动力与机械学院硕士研究生。主要研究方向为材料加工工艺及设备。E-mail:cichee@163.com。朱援祥(通信作者)，男，1963年生。武汉大学动力与机械学院副教授、博士。周立武，男，1986年生。武汉大学动力与机械学院硕士研究生。周 兵，男，1966年生。中国三峡集团建设管理公司工程检测中心工程师。