考虑多退化失效和突发失效之间竞争失效的可靠性评估方法

刘晓娟 王华伟 徐 璇南京航空航天大学民航学院，南京，211106

考虑多退化失效和突发失效之间竞争失效的可靠性评估方法

刘晓娟 王华伟 徐 璇
南京航空航天大学民航学院，南京，211106

提出了考虑多退化失效和突发失效之间竞争失效的可靠性评估方法。由协方差分析了多元退化信息之间的相关性及相关程度，建立多退化失效模式的可靠性评估模型，且选用了多元正态分布来建立模型。构建基于退化量突发失效的条件概率，分析退化失效对突发失效的影响，通过多个退化模式的退化失效与突发失效的联合概率分布函数建立竞争失效的可靠性评估模型。最后以航空发动机的失效数据为例，验证了模型的有效性。

多退化失效模式；突发失效；系统可靠性评估；竞争失效

0 引言

随着现代科学和技术的迅速发展，产品越来越复杂，系统的失效模式也趋于多样化，因此对产品可靠性分析与评估提出了更高的要求。从失效机理上看，系统的失效一般可分为两大类，即退化失效和突发失效。复杂系统在运行期间，并不只有正常运行和失效两种状态，而是一个连续的退化过程。系统的退化失效是指系统的性能随着时间的增加逐渐退化，超过一定的阈值后系统失效，一般分为连续平滑的自然退化和冲击(极端冲击、累计冲击、连续冲击、δ冲击)导致的退化失效[1]。在退化过程中，冲击会导致系统失效率和退化量增大[2]，另一方面自然退化会影响冲击的失效阈值[3]。所以冲击和自然退化之间存在相关性和竞争性。突发失效是指系统的功能突然完全丧失导致系统失效，所以突发失效的产品只有两种状态，即正常或失效。复杂系统的失效并不是单一失效模式的作用，往往是多种不同失效模式之间竞争的结果。这些失效模式之间的竞争遵循着一种竞争规则，那就是任何一种失效模式的发生导致系统失效后，其他失效模式将不再发生[4-5]，即系统的失效是由最早出现的失效模式导致的。突发失效与退化失效之间往往存在着一定的联系，所以必须要考虑多种退化失效模式之间及退化失效与突发失效之间的相关性及相互作用，避免低估或高估系统的可靠性。

赵建印等[6-7]采用回归模型，以金属化膜脉冲电容器为例建立竞争失效模型。PENG等[8]建立了多种相关性的竞争失效系统的可靠性模型。唐家银等[9]利用Copular相关性理论，分别给出了相对失效阈值、随机失效阈值-退化量相干作用下的多故障模式相关性失效的综合可靠性评估模型。陈铁等[10]提出了一种基于竞争风险理论的多失效模式统计相关性分析模型，采用多元对数正态分布建立系统的联合失效分布，用p值假设检验来判别各竞争失效模式间的相关性。常春波等[3]研究了系统受到δ冲击时，自然退化和冲击两个竞争性失效过程间的相关性，建立了系统可靠度模型。SU等[11]研究了退化和冲击过程，建立了相关竞争失效模型，对受退化和随机冲击共同作用的产品进行可靠性评估，并且分析了失效阈值的变化对可靠性的影响。WU等[12]将模糊推理Petri网与零件计数可靠性预测相结合，来预测复杂机械系统在设计早期阶段的可靠性。LIU等[13]用比例危险模型来描述组件间退化的相互作用，应用多状态系统理论来估计系统的可靠性，并利用Monte Carlo方法对系统的伪寿命进行抽样。

上述研究一般只考虑多种退化失效模式之间或一种退化失效和一种突发失效之间的竞争失效问题。针对复杂系统运行过程中往往存在多种退化失效和突发失效并存的情况，本文研究了多个退化模式引起的退化失效与突发失效之间的竞争失效问题，首先判断多种退化失效模式之间的相关性，并选用多元正态分布来建立多退化失效模式的可靠性评估模型，然后通过退化量条件下突发失效的条件概率来分析退化失效对突发失效的影响，最后建立多个退化模式的退化失效与突发失效的联合概率分布函数，并对系统进行可靠性评估。

1 多退化失效模式下可靠性评估模型

1.1 多元退化信息间相关性的分析

对于多退化模式下的产品来说，任何一种退化模式的退化量首先达到失效阈值即Xi(t)>Di，则

系统失效或停止工作。多元退化模式下产品的竞争失效如图1所示。

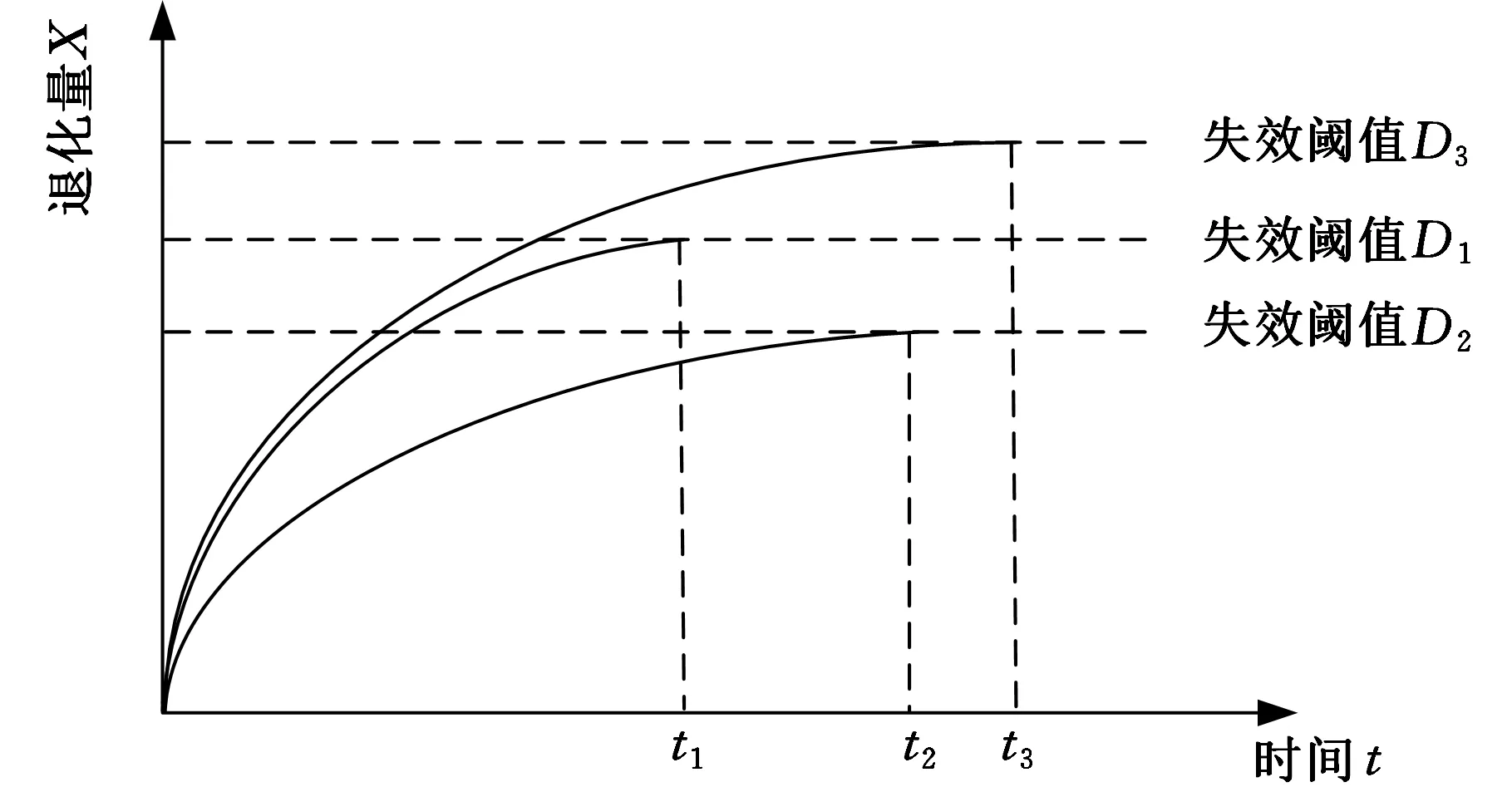
图1 多元退化模式下产品的竞争失效Fig.1 The competing failure of multi-degradation failure

产品的多个退化模式之间存在相关或独立的关系。如果这些退化模式之间是相互独立的，则可以将其当作串联系统进行处理。如果这些退化模式相关，则建立多元退化量的联合概率密度函数，然后根据概率密度函数来估计产品的可靠度。在进行系统可靠性评估时，首先要判别各退化模式间的相关性及相关程度，再对其进行可靠度计算。

假设有n个随机样本在进行退化试验，在时刻t1,t2,…,tm记录各个样本的退化数据，有p个独立的退化失效模式，对应的退化量记为Xi(t),i=1,2,…,p。Xi(t)是一个关于时间的随机变量，每个退化量对应一个失效阈值Di，当退化量Xi(t)达到失效阈值Di时，发生退化失效。任何一个退化量达到失效阈值，均会导致整个系统失效。对于所有的样本，各退化量的测量时间与测量次数都是相同的，如果试验过程中有样本发生失效，则该样本退出试验。退化量之间的相关性可用协方差来评判，协方差矩阵为

(1)

在式(1)中，协方差可以用下式计算：

(2)

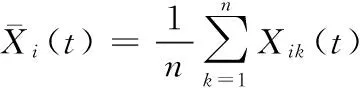
若cov(Xi(t),Xj(t))≠0，则第i个退化量与第j个退化量是相关的，否则两者独立。当两个退化量的协方差接近0时，它们之间的相关性很弱，可以认为它们是独立的。所以协方差不仅可以判别任意两个退化量之间的相关性，还可以用来估计相关的两个退化量之间的相关程度，协方差越大表明相关性越强。

1.2 建立多退化失效的可靠性评估模型

如果各个退化模式之间是相互独立的，则系统可以看成一个串联系统，其可靠度为

(3)

如果退化模式之间是相关的则系统就不可以看作简单的串联系统，在求可靠度时，不能将各个模式的可靠度直接连乘，可以先估计出系统中所有退化量的联合概率密度函数，再根据联合概率密度函数计算系统的可靠度：

(4)

其中，f(x1(t),x2(t),…,xp(t))表示t时刻p个退化量的联合概率密度函数。求出联合概率密度函数即可估计出可靠度。但是对于复杂且退化模式比较多的系统，确定其退化的联合概率密度函数的难度较大。当系统处于平稳运行期，系统的失效往往体现为多种失效模式的随机扰动，这时系统的寿命概率分布近似服从正态分布[14]。基于此，我们可以选用多元正态分布，它是一种常用的失效时间分布，用此分布建立的模型是最常用的竞争失效模式相关性统计可靠性模型。

多元正态分布的联合概率密度函数的表达式如下[15]：

(5)

式中，X=(x1,x2,…,xp)T为多元退化向量；Σ为协方差矩阵；|Σ|为协方差矩阵的行列式；μ=(μ1,μ2,…，μp)T为退化量的均值向量。

2 竞争失效的可靠性建模

设t时刻退化量的分布函数为Gs(x1t,x2t,…,xpt)，其相应的概率密度函数为gs(x1t,x2t,…,xpt)，用Tsi表示第i种退化模式导致系统失效的时间，Tsi为随机变量。

突发失效出现的概率可能与退化量有关。用Thj(j=1,2,…,m)表示第j种突发失效模式导致系统失效的时间，该时间为随机变量。记突发失效的失效率函数为λhj(t,x)，τ是时间t的积分变量，则系统在第j种突发失效模式下的可靠度函数为

(6)

条件概率密度函数为

(7)

t时刻系统发生多突发失效的可靠度函数为

(8)

在竞争失效模式下，任何一个失效模式的发生都会导致系统失效，所以t时刻系统的可靠度为

(9)

将式(5)代入式(9)，得退化量服从正态分布情况下，t时刻系统的可靠度：

(10)

3 实例分析

航空发动机是一个复杂的系统，它的失效模式有机械磨损、滑油泄漏、汽路性能退化、叶片与高压涡轮罩损伤等[16-17]，其失效就是多种失效模式之间竞争的结果。本文选取某航空公司同一时期内投入使用的15台航空发动机的排气温度裕度(EGTM)和燃油消耗量偏差(DWF)这两个性能参数作为数据样本，如表1所示。数据来源于两个方面，一是航空发动机运行过程中实际采集到的数据，二是依据航空发动机的退化速率采用插值法和蒙特卡罗仿真方法获取。这样构造数据保证了足够的样本信息，能够更加全面反映发动机运行情况。EGTM的失效阈值D1=26，DWF的失效阈值D2=2.3，样本数据服从正态分布。

(1)根据式(1)由MATLAB计算出各个时刻的协方差矩阵，如表2所示。从表中的数据可判断出EGTM与DWF之间具有相关性，而且随着时间的增加，两者的相关性越来越强。

(2)根据样本数据的退化信息分别求出各个时刻的EGTM的样本均值μx1(t)和样本标准差σx1(t)以及DWF的样本均值μx2(t)和样本标准差σx2(t)，如表3和表4所示。当发动机4、6、11、13号样本的EGTM退化量各自达到29、46、26、20时，发动机发生突发失效，其对应的突发失效可靠度Rh(x)分别为14/15、13/15、12/15、11/15。从表1样本数据可以看出突发失效出现在整个退化过程中，说明在此竞争失效模型中，突

表1 航空发动机EGTM和DWF的数据表
Tab.1 EGTM and DWF data of aero-engine

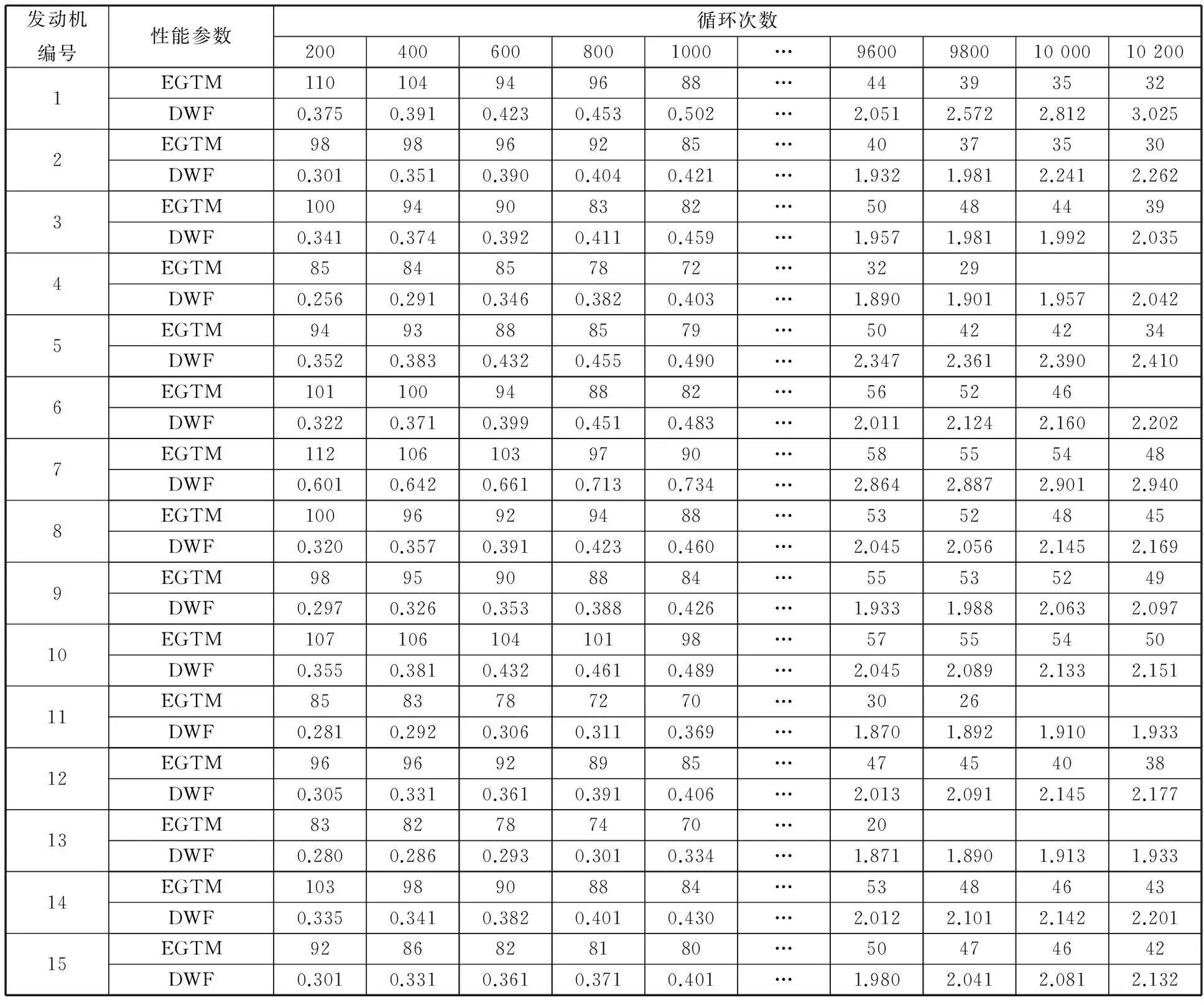
发动机编号性能参数循环次数2004006008001000…9600980010000102001EGTM110104949688…44393532DWF0.3750.3910.4230.4530.502…2.0512.5722.8123.0252EGTM9898969285…40373530DWF0.3010.3510.3900.4040.421…1.9321.9812.2412.2623EGTM10094908382…50484439DWF0.3410.3740.3920.4110.459…1.9571.9811.9922.0354EGTM8584857872…3229DWF0.2560.2910.3460.3820.403…1.8901.9011.9572.0425EGTM9493888579…50424234DWF0.3520.3830.4320.4550.490…2.3472.3612.3902.4106EGTM101100948882…565246DWF0.3220.3710.3990.4510.483…2.0112.1242.1602.2027EGTM1121061039790…58555448DWF0.6010.6420.6610.7130.734…2.8642.8872.9012.9408EGTM10096929488…53524845DWF0.3200.3570.3910.4230.460…2.0452.0562.1452.1699EGTM9895908884…55535249DWF0.2970.3260.3530.3880.426…1.9331.9882.0632.09710EGTM10710610410198…57555450DWF0.3550.3810.4320.4610.489…2.0452.0892.1332.15111EGTM8583787270…3026DWF0.2810.2920.3060.3110.369…1.8701.8921.9101.93312EGTM9696928985…47454038DWF0.3050.3310.3610.3910.406…2.0132.0912.1452.17713EGTM8382787470…20DWF0.2800.2860.2930.3010.334…1.8711.8901.9131.93314EGTM10398908884…53484643DWF0.3350.3410.3820.4010.430…2.0122.1012.1422.20115EGTM9286828180…50474642DWF0.3010.3310.3610.3710.401…1.9802.0412.0812.132

表2 EGTM和DWF在各时刻的协方差矩阵
Tab.2 The covariance matrix of EGTM and DWF at various points

循环次数200400600…1000010200协方差矩阵77.11430.50540.50540.0065éëêêùûúú63.35240.45010.45010.0071éëêêùûúú58.54290.48100.48100.0017éëêêùûúú…382.40952.46542.46540.0872éëêêùûúú384.85711.82781.82783.0239éëêêùûúú

表3 EGTM的样本均值和样本标准差
Tab.3 The sample mean and standard deviation of EGTM

循环次数2004006008001000…960098001000010200μx197.6094.7390.4087.0782.47…46.3341.8736.1330.00σx18.7817.9597.6518.4047.633…11.2114.6019.5519.61

表4 DWF的样本均值和样本标准差
Tab.4 The sample mean and standard deviation of DWF

循环次数2004006008001000…960098001000010200μx20.33480.36320.39480.42110.4538…2.05472.13032.19902.2473σx20.08030.08440.08420.09380.0910…0.25160.27650.29530.3226

发失效与退化程度相关。假设本组样本的突发失效可靠度服从双参数威布尔分布，a是形状参数，b是尺度参数，即

(11)

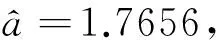
求得各个时刻的可靠度如表5所示。

此航空发动机发生竞争失效的可靠度函数如图2所示,可以看出，发动机在运行的初期，可靠度几乎不变，随着运行时间越来越长，可靠度逐渐

表5 航空发动机各时刻的可靠度评估值
Tab.5 The estimation of aero-engine reliability at various points

循环次数2004006008001000…9600980010000R(t)1.00001.00000.99990.99960.9993…0.73830.54860.3040

下降，发动机性能开始退化，这主要是由于在外力作用下，一些零部件出现磨损、疲劳、腐蚀等。单纯的退化失效使得可靠性缓慢下降，但是在9000 h至10 000 h左右，发动机的可靠性急速下降。这主要是由于各个发动机在此段时间退化时已经开始发生突发失效，所以可靠性下降的速度不断增大，最常见的就是发动机的结构件疲劳断裂。由此可以看出，在竞争失效的情况下，系统的可靠性下降较快。考虑航空发动机的竞争失效，可以更准确地评估其可靠性，制定合理的维修方案，避免维修不当，减少维修成本，实现航空发动机的健康管理。

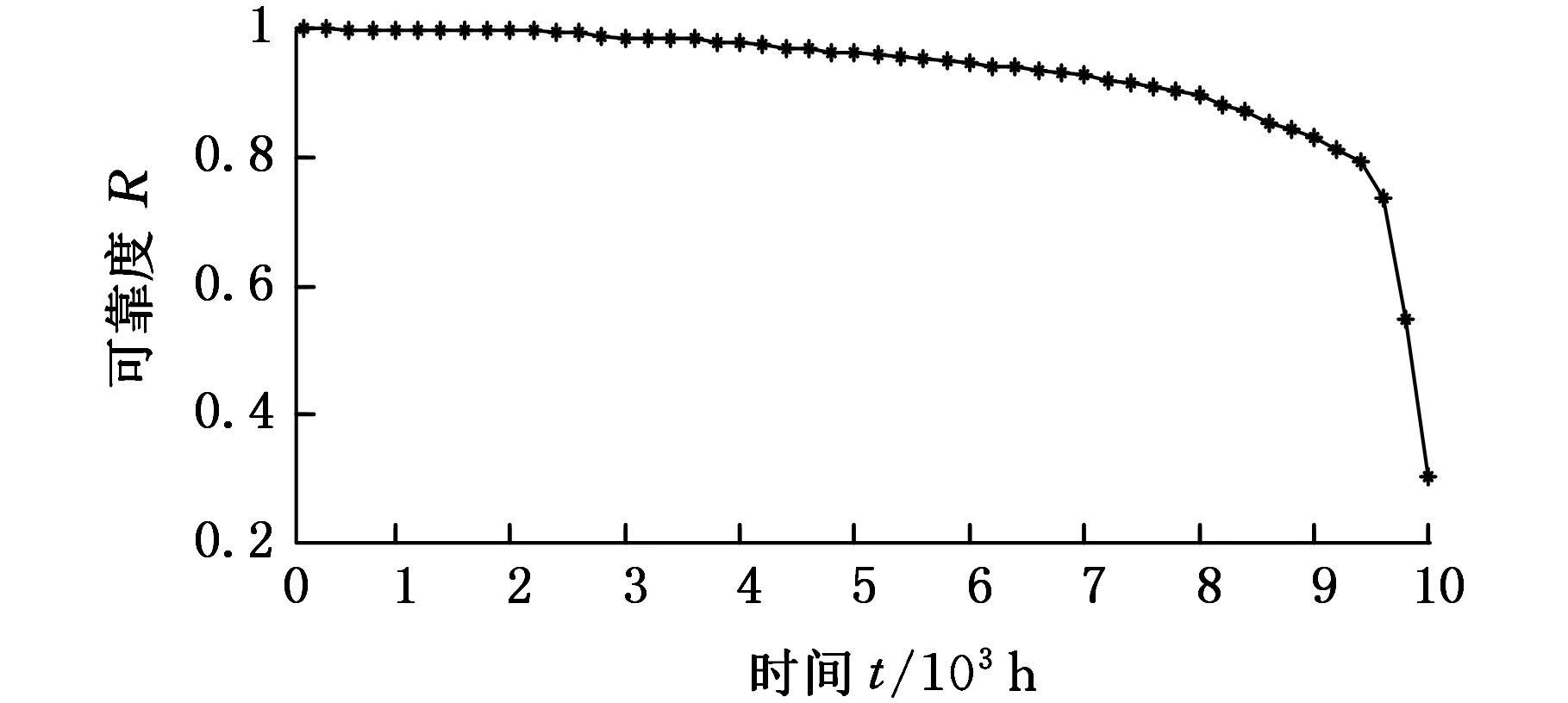
图2 竞争失效的可靠度函数曲线图Fig.2 The reliability function curve of competing failure

4 结束语

本文针对复杂系统同时存在多种退化失效模式的情况，研究了多退化失效模式与突发失效的竞争失效问题，建立了多种失效模式间可靠性评估的一般模型，定量分析了各种失效模式在竞争失效中的关系和作用机制。并以航空发动机为例，分析航空发动机排气温度裕度和燃油消耗量偏差这两个性能参数退化量之间的相关性，以及在退化过程中退化失效对突发失效的影响，最终求出竞争失效下的可靠度并给出可靠度曲线图，验证了模型的有效性。下一步将更加细致地分析系统所存在的各种失效模式及失效机理，为长寿命复杂系统的可靠性评估提供更为准确的方法和新思路。

[1] NOOROSSANA R, SABRI-LAGHAIE K. Reliability and Maintenance Models for a Dependent Competing-risk System with Multiple Time-scales[J]. Proceedings of the Institution of Mechanical Engineers Part O: Journal of Risk & Reliability, 2015, 229(2):131-142.

[2] WANG Z, HUANG H Z, LI Y, et al. An Spproach to Reliability Assessment under Degradation and Shock Process[J]. IEEE Transactions on Reliab-ility, 2011, 60(4):852-863.

[3] 常春波, 曾建潮. δ冲击条件下相关性竞争失效过程的系统可靠性建模[J]. 振动与冲击, 2015(8):203-208. CHANG Chunbo, ZENG Jianchao. Reliability Modeling for Dependent Competing Failure Processes under δ-shock[J]. Journal of Vibration and Shock, 2015(8):203-208.

[4] HUANG W, ASKIN R G. Reliability Analysis of Electronic Devices with Multiple Competing Failure Modes Involving Performance Aging Degradation[J]. Quality & Reliability Engineering, 2003, 19(3):241-254.

[5] DAVID H A. The Theory of Competing Risks[J]. Journal of the Operational Research Society, 1979, 30(7):675-676.

[6] 赵建印. 基于性能退化数据的可靠性建模与应用研究[D].长沙：国防科学技术大学，2005. ZHAO Jianyin. Study on Reliability Modeling and Applications Based on Performance Degtadation[D]. Changsha: National University of Defense Technology, 2005.

[7] 赵建印，刘芳，孙权，等. 基于竞争失效模型的金属化膜脉冲电容器产品可靠性研究[J]. 系统工程理论与实践，2006,26(1):60-64. ZHAO Jianyin, LIU Fang, SUN Quan, et al. Reliability Analysis of Metalized-film Pulse Capacitor under Competing Failure Modes[J]. System Engineering Theory and Practice, 2006, 26(1):60-64.

[8] PENG H, FENG Q M, COIT D W. Reliability and Maintenance Modeling for Systems Subject to Multiple Dependent Competing Failure Processes[J]. IIE Transactions, 2010, 43(1):12-22.

[9] 唐家银，何平，梁红琴,等. 多故障模式高长寿命产品相关性失效的综合可靠性评估[J]. 机械工程学报，2013，49(12)：176-182. TANG Jiayin, HE Ping, LIANG Hongqin, et al. Comprehensive Reliability Assessment of Long-life Products with Correlated Multiple Failure Modes[J]. Journal of Mechanical Engineering, 2013, 49(12):176-182.

[10] 陈铁，郑松林，刘新田,等. 基于竞争风险的燃料电池发动机多失效模式统计相关性分析[J]. 汽车工程，2015,37(3):266-270. CHEN Tie, ZHENG Songlin, LIU Xintian, et al. Statistical Correlation Analysis on the Multiple Failure Modes of a Fuel Cell Engine Based on Competing Risks[J]. Automotive Engineering, 2015, 37(3):266-270.[11] SU Chun, QU Zhongzhou, HAO Huibing. Reliability Assessment Considering Dependent Competing Failure Process and Shifting-threshold[J]. Journal of Southeast University (English Edition), 2013, 29(1):52-56.

[12] WU J, YAN S. An Approach to System Reliability Prediction for Mechanical Equipment Using Fuzzy Reasoning Petri Net[J]. Proceedings of the Institution of Mechanical Engineers Part O: Journal of Risk & Reliability, 2013, 228(1):39-51.

[13] LIU J, LI X, PENG C. Reliability Analysis for Multi-component Degraded System Subject to Multiple Dependent Competing Failure Process[C]// Prognostics and System Health Manageme-nt Conference. Beijing, 2015:7380060.

[14] 王华伟, 高军, 吴海桥. 基于贝叶斯模型平均的航空发动机可靠性分析[J]. 航空动力学报, 2014, 29(2):305-313. WANG Huawei, GAO Jun, WU Haiqiao. Reliability Analysis on Aero-engine Using Bayesian Model Averaging[J]. Journal of Aerospace Power, 2014, 29(2):305-313.

[15] 孙尚拱. 应用多变量统计分析[M]. 北京：科学出版社，2011:22-23. SUN Shanggong. Applied Multivariate Statistical Analysis[M]. Beijing: Science Press, 2011:22-23.

[16] 宋兆泓. 航空发动机典型故障分析[M]. 北京：北京航空航天大学出版社，1993:2-4. SONG Zhaohong. Typical Failure Analysis of Aero-engine[M]. Beijing: Beihang University Press, 1993:2-4.

[17] FANG B. Average Life Prediction for Aero-engine Fleet Based on Performance Degradation Data[C]//Prognostics and System Health Manageme-nt Conference. Macau, 2010:1-6.

(编辑 王旻玥)

Reliability Assessment Based on Competition Failure Considering Multi-degradation and Catastrophic Failure

LIU Xiaojuan WANG Huawei XU Xuan

College of Civil Aviation,Nanjing University of Aeronautics and Astronautics, Nanjing, 211106

A reliability assessment method of the competing failure during multi-degradation failure and the catastrophic failure was proposed. Covariance was used to analyze the dependence and the degree of correlation during multivariate degradation information, reliability assessment model of multi-degradation mode was developed. In addition, multivariate normal distribution was used to establish the model. The conditional probability of catastrophic failure under the degradation data was developed to analyze the effects of degradation failure on catastrophic. Reliability assessment model of competition failure was developed through the joint probability distribution function of multi-degradation mode and catastrophic failure. Finally, an example of the failure data of aero engine verified the effectiveness of proposed method.

multi-degradation mode; catastrophic failure; system reliability assessment; competing failure

2016-01-20

国家自然科学基金与中国民航局联合基金资助项目(U1233115)；国家自然科学基金资助项目(71401073)

TB114.3

10.3969/j.issn.1004-132X.2017.01.002

刘晓娟，女，1991年生。南京航空航天大学民航学院硕士研究生。主要研究方向为航空器系统可靠性与安全性。E-mail:juanjuan199136@126.com。王华伟(通信作者)，女，1974年生。南京航空航天大学民航学院教授、博士研究生导师。徐 璇，女，1992年生。南京航空航天大学民航学院硕士研究生。