采煤机截割部传动系统的非线性动力学建模及仿真

毛 君 张 瑜 张 坤 陈洪月 徐健博辽宁工程技术大学机械工程学院，阜新,123000

采煤机截割部传动系统的非线性动力学建模及仿真

毛 君 张 瑜 张 坤 陈洪月 徐健博
辽宁工程技术大学机械工程学院，阜新,123000

针对采煤机截割部齿轮传动系统在运行中产生振动、制造噪声污染等现象，综合考虑啮合刚度、啮合阻尼、综合误差等因素，建立了采煤机截割部齿轮传动系统的非线性动力学模型，运用变步长Runge-Kutta方法对系统微分方程进行了求解。通过分析相平面图和庞加莱截面研究了啮合刚度、阻尼比及激振频率对齿轮系统动态特性的影响。研究结果表明：在一定区间内，阻尼比逐渐减小时，太阳轮位移响应由单周期运动转为多周期运动，最终进入混沌运动；啮合刚度增大时，太阳轮位移响应同样从周期运动逐渐进入混沌运动；激振频率逐渐增大时，太阳轮位移响应呈现由周期响应转变为混沌响应再转变为拟周期响应的现象。

采煤机截割部；行星齿轮传动系统；非线性动力学；动力学微分方程

0 引言

截割部齿轮传动系统是采煤机重要组成部分，它在运行中，不仅会产生振动，还会制造噪声污染，因此有必要对采煤机截割部齿轮系统振动规律及动态特性进行深入研究[1-2]。

国内外学者对行星齿轮系统的非线性进行了大量研究。Lin等[3]对行星齿轮啮合刚度变化引起的参数不稳定性进行了相关研究；Bark等[4]研究了行星齿轮传动非线性动力学的解析解；Eritenel等[5]采用弯-扭-轴-摆耦合模型分析了斜齿行星齿轮传动的固有特性；文献[6-7]考虑齿轮副的综合啮合误差，建立了等效多自由度系统振动的力学模型，研究了不同齿轮啮合刚度条件下的系统振动特性，并分别对正交面和非正交面齿轮系统的非线性振动特性进行了深入研究；王世宇等[8]采用行星传动纯扭转模型对传动系统的固有特性进行了研究；孙涛等[9]对行星齿轮系统的非线性动力学问题进行了研究；公彦军[10]建立了汽车自动变速器多级行星齿轮传动系统的动力学模型，分析了自然模态和误差激励对系统固有特性的影响规律；黄启林[11]结合公彦军[10]的研究分析，建立了两级行星传动系统的动力学模型，研究了时变啮合刚度及齿侧间隙等因素对系统非线性动态特性的影响规律。

本文多方面考虑啮合刚度、啮合阻尼、综合误差等因素影响，建立采煤机截割部齿轮传动系统的非线性动力学模型，运用变步长Runge-Kutta方法对系统微分方程进行数值求解，通过分析相平面图和庞加莱截面研究啮合刚度、阻尼比及激振频率对采煤机截割部齿轮传动系统非线性动态特性的影响。

1 采煤机截割部传动系统力学模型

本文采用集中质量法建立采煤机截割部齿轮传动系统的动力学模型，为研究啮合刚度、阻尼比、激振频率等因素对系统动态特性的影响，需作如下假设：①假设齿轮主体质量为集中一点的参数扭振系统；②假设内齿圈质量无限大，且忽略其波动；③将齿轮传动系统中的齿轮看作直齿轮；④忽略齿轮轴、输入轴、输出轴及轴承等对系统的影响；⑤齿轮系统为刚性系统，采用刚度、阻尼元件对啮合部分进行描述；⑥忽略摩擦力对系统的影响；⑦忽略齿轮载荷对齿轮系统产生的惯性影响。

采煤机截割部齿轮传动系统结构示意图见图1。截割部在截割过程中所受载荷变化较大，且随机性大，这加剧了传动齿轮、轴承等关键零件的损坏。因此，研究采煤机截割部各级齿轮啮合的动态特性，对延长截割部零件使用寿命，增强其抗振能力，提高采煤机的工作可靠性和稳定性具有重大的意义。

采煤机截割部齿轮传动系统主要包括：Zi(i=1，2，…，8)表示第i个齿轮，sj(j=1，2)表示第j级太阳轮，pij表示第j(j=1，2)级行星架的第i(i=1，2，3)个行星轮，cj(j=1，2)表示第j级行星架，rj(j=1,2)表示第j级内齿圈，且内齿圈固定，忽略啮合过程中产生的摩擦，则截割部摇臂齿轮传动系统非线性动力学模型如图2所示。

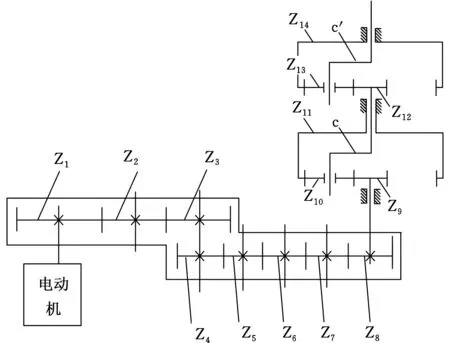
Z1—齿轮1 Z2—齿轮2 Z3—齿轮3 Z4—齿轮4Z5—齿轮5 Z6—齿轮6 Z7—齿轮7 Z8—齿轮8Z9—一级太阳轮 Z10—一级行星轮 Z11—一级内齿圈Z12—二级太阳轮 Z13—二级行星轮 Z14—二级内齿圈c—一级行星架 c′—二级行星架图1 采煤机截割部齿轮传动系统结构示意图Fig.1 The motion diagram of cutting part and shearer rocker gear transmission system

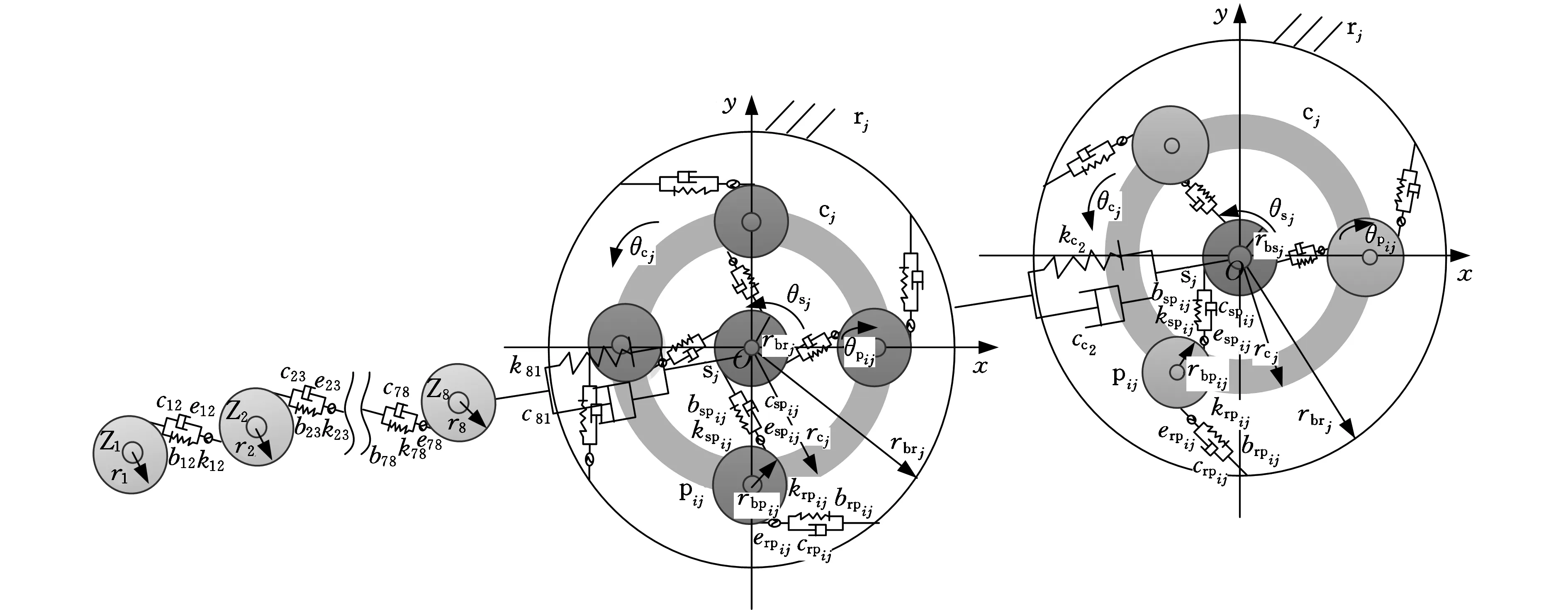
图2 采煤机截割部齿轮传动系统非线性动力学模型Fig.2 The nonlinear dynamic model of cutting part and shearer rocker gear transmission system

齿轮Zi的齿数为zi，其角位移采用θi描述，ri为齿轮Zi的基圆半径，齿轮Zi和齿轮Zj的啮合刚度、啮合阻尼系数、半齿侧间隙、静态啮合误差采用kij、cij、bij、eij描述，其中i=1,2,…,7，j=2,3,…,8；k81、c81为齿轮Z8与第一级太阳轮的啮合刚度及啮合阻尼系数；xij(i=1,2,…,7；j=2,3,…,8)为齿轮Zi角位移与齿轮Zj角位移相互作用的接触线上产生的相对位移；θsj、θcj、θpij(j=1，i=1，2，3，4；j=2，i=1，2，3)分别为第j级太阳轮、第j级行星架、第j级行星架的第i个行星轮的角位移；rbsj、rbpij(j=1，i=1，2，3，4；j=2，i=1，2，3)、rbcj分别为第j级太阳轮、第j级行星架的第i个行星轮、第j级内齿圈的基圆半径；rcj(j=1,2)为第j级行星架基圆半径；kspij(j=1，i=1，2，3，4；j=2，i=1，2，3)为第j级太阳轮与第j级行星架第i个行星轮的啮合刚度，其啮合阻尼系数为cspij，半齿侧间隙为bspij，综合啮合误差为espij；krpij(j=1，i=1，2，3，4；j=2，i=1，2，3)为第j级内齿圈与第j级行星架第i个行星轮组成的内啮合副的啮合刚度，其啮合阻尼系数为crpij，半齿侧间为brpij，综合啮合误差为erpij；第j级太阳轮的齿数采用zsj(j=1,2)描述，相应的第i个行星轮的齿数采用zpij(j=1，i=1，2，3，4；j=2，i=1，2，3)描述，zrj(j=1,2)为第j级内齿圈的齿数。

2 动力学微分方程

通过对截割部摇臂直齿轮、太阳轮、行星轮以及行星架动力学模型分析，可以得到整个系统的动力学方程：

(1)

各弹性恢复力及阻尼力可表示为

其中，f为间隙非线性函数，其表达式为

弹性恢复力及阻尼力中各啮合刚度、啮合误差及啮合阻尼表示为

kij(t)=kmij(1+σ′sin(Ωt+φij))
kspij(t)=kmsij(1+σsin(Ωt+φspij))
krpij(t)=kmrij(1+σ″sin(Ωt+φrpij))

eij(t)=em+eijjcos(Ωt+θij)
espij(t)=Aspijsin(Ωt+βsij)
erpij(t)=Arpijsin(Ωt+βrij+γsrj)

式中，kmij为第Zi、第Zj齿轮的平均啮合刚度；kaij为第i、第j齿轮刚度幅度的平均涨幅程度；Ω为齿轮的激振频率；φij为相位角；kmsij为第j级第i个行星轮外啮合相互作用平均刚度；kasij为第j级第i个行星轮外啮合相互作用过程中刚度的最大幅值；kmrij为第j级第i个行星轮内啮合相互作用过程中平均刚度的变化值；karij为第j级第i个行星轮内啮合相互作用过程中刚度的最大幅值；em为齿轮误差平均幅值；eijj为误差分量的幅值；θij为相位角；Aspij为第j级第i个行星轮外啮合相互作用副误差的最大幅值；Arpij为第j级第i个行星轮内啮合相互作用副误差的最大幅值；βsij为第j级第i个行星轮外啮合相互作用副静误差的初相位；βrij为第j级第i个行星轮内啮合相互作用副静误差的初相位；γsrj为第j级外齿轮啮合相互作用副的相位差;ζ为直齿轮啮合的阻尼比；mi为第i(i=1,2,…,7)个直齿轮的质量；mj为第j(j=i+1)个直齿轮的质量；msj(j=1，2)为第j级太阳轮的质量；mpij(j=1，i=1，2，3，4；j=2，i=1，2，3)为第j级第i个行星轮的质量；mrj(j=1，2)为第j级内齿圈的质量。

在行星齿轮系统中，齿轮副之间存在齿侧间隙，系统的约束不完整，即系统的动力学方程为半正定系统，其方程解为非确定值。为了减小刚体位移对系统产生的影响，对整个方程组的求解进行降维，假设如下：

(2)

式中,xsj为第j级太阳轮线位移;xcj为第j级行星架线位移；xpij(j=1，i=1，2，3，4；j=2，i=1，2，3)为第j级行星架的第i个行星轮线位移；xscj(j=1,2)为第j级内外啮合相互作用线上的位移叠加；xspij(j=1，i=1，2，3，4；j=2，i=1，2，3)为第j级太阳轮与第j级第i个行星轮啮合相互作用的位移；xrpij(j=1，i=1，2，3，4；j=2，i=1，2，3)为第j级内齿圈和第j级第i个行星轮啮合相互作用的位移。

令xi=θiri(i=1,2,…,8)，xsj=θsjrbsj(j=1,2)，xcj=θcjrbcj(j=1,2)，xpij=θpijrbpij(j=1，i=1，2，3，4；j=2，i=1，2，3)，则式(1)整理为

(3)

(4)

(5)

3 系统非线性动态特性仿真

从动力学角度出发，综合考虑齿轮刚度激励、啮合冲击激励、误差激励等因素，研究采煤机截割部齿轮传动系统非线性振动特性，采用变步长Runge-Kutta方法对上述动力学微分方程进行求解。由于第一级和第二级行星齿轮系统的太阳轮仿真结果基本一致，本文仅对第一级行星齿轮系统的太阳轮进行分析。

3.1 不同阻尼比下系统的响应

对于齿轮系统的线性振动，阻尼比仅对振幅有一定的影响，对齿轮系统的振动形式和性质产生的影响不大，当考虑行星齿轮系统中存在非线性振动因素时，分析阻尼比对系统的影响则至关重要，当阻尼比ζ分别为0.2、0.1、0.05时，系统响应如图3～图11所示。

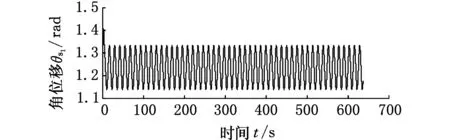
图3 ζ=0.2时太阳轮位移曲线Fig.3 The sun gear displacement curves(ζ=0.2)

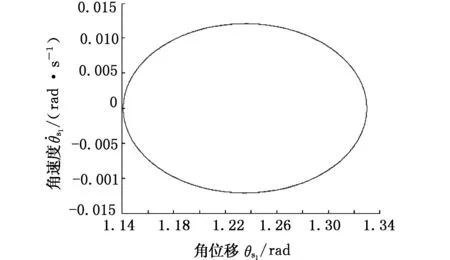
图4 ζ=0.2时太阳轮位移响应相平面图Fig.4 The sun gear displacement response of phase plane diagram(ζ=0.2)

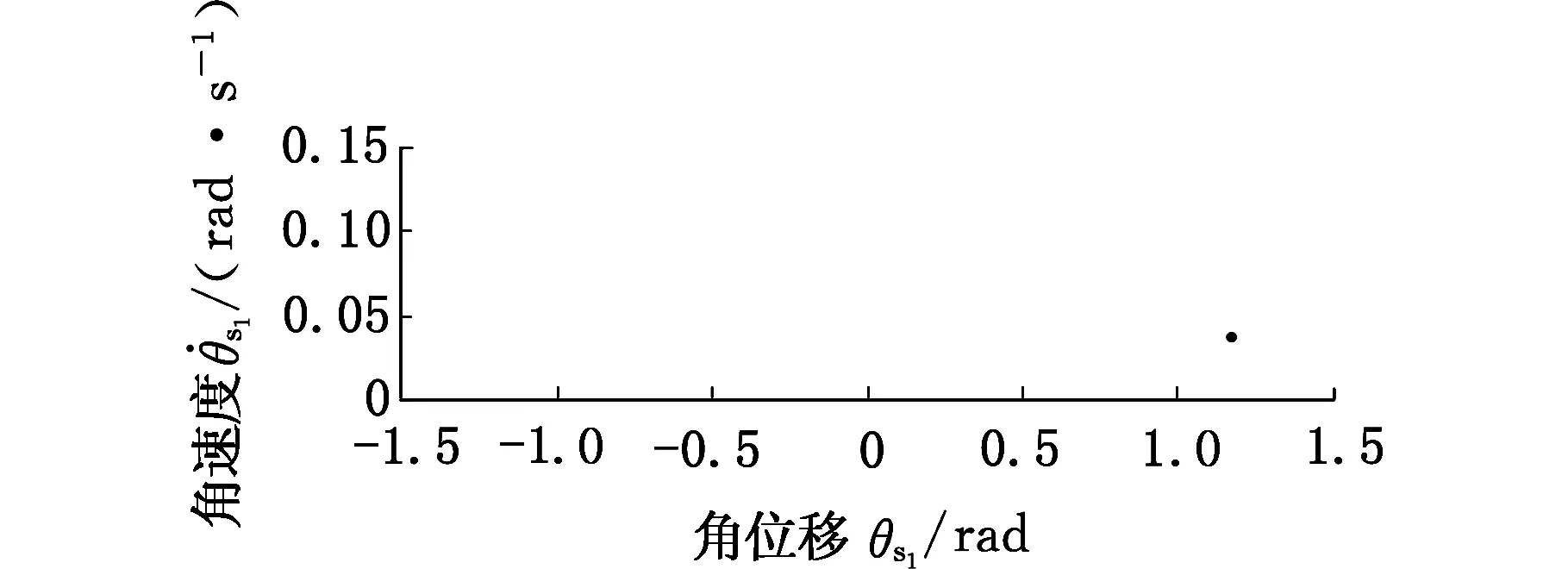
图5 ζ=0.2时太阳轮位移响应庞加莱截面Fig.5 The sun gear displacement response of Poincare section(ζ=0.2)

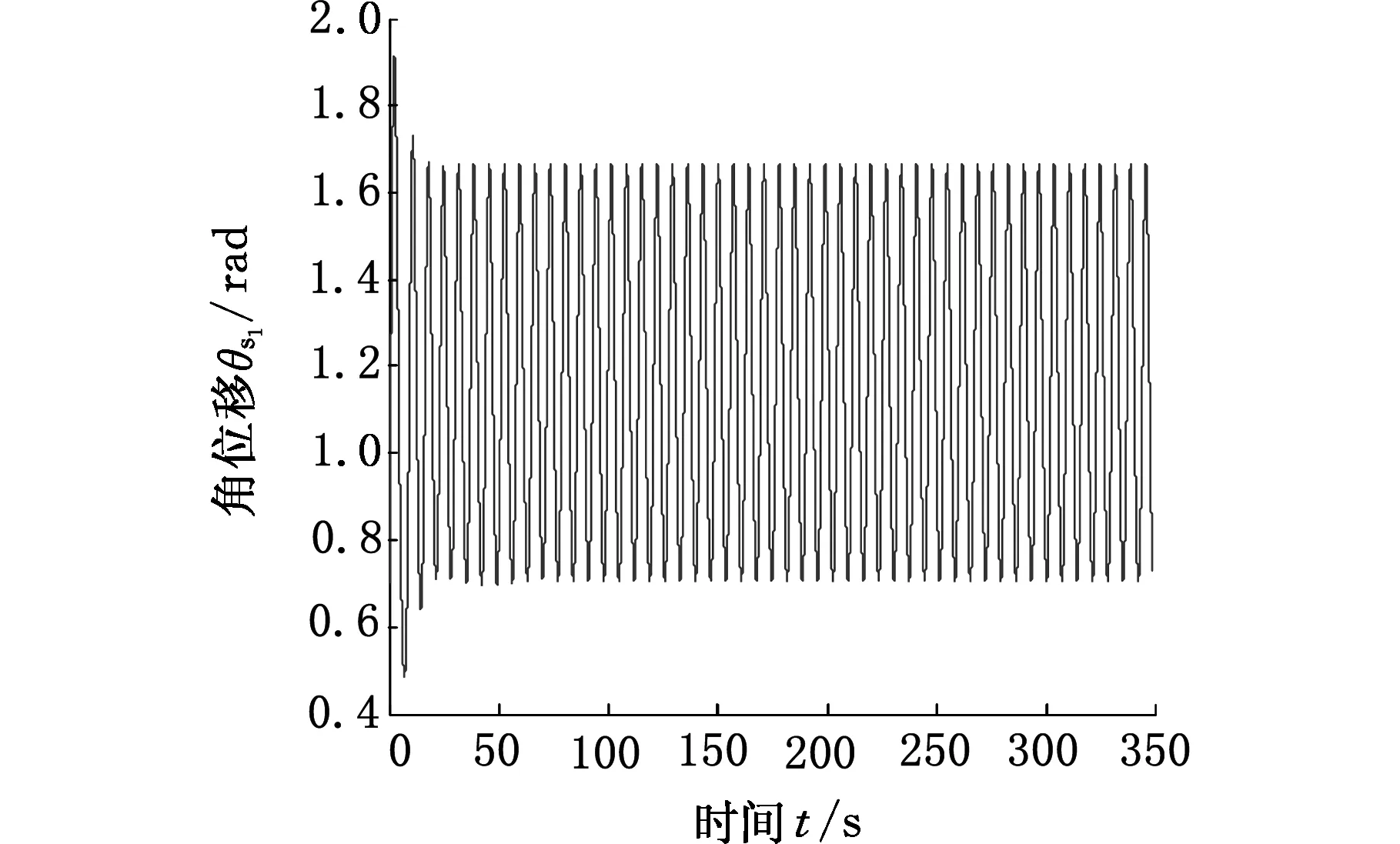
图6 ζ=0.1时太阳轮位移曲线Fig.6 The sun gear displacement curves(ζ=0.1)

通过对比不同阻尼比下行星齿轮系统的太阳轮位移响应结果可知，随着阻尼比逐渐减小，行星齿轮系统的太阳轮位移响应由单周期运动变化到多周期运动，最终进入混沌运动状态，系统的振动幅度呈增大趋势。由此可得：在一定范围内，阻尼比能够对系统响应幅值产生抑制，即阻尼比越大，振动的振幅越小，反之，齿轮系统的非线性现象越明显，易产生混沌现象。

图7 ζ=0.1时太阳轮位移响应相平面图Fig.7 The sun gear displacement response of phase plane diagram(ζ=0.1)

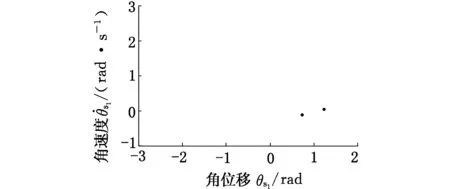
图8 ζ=0.1时太阳轮位移响应庞加莱截面Fig.8 The sun gear displacement response of Poincare section(ζ=0.1)

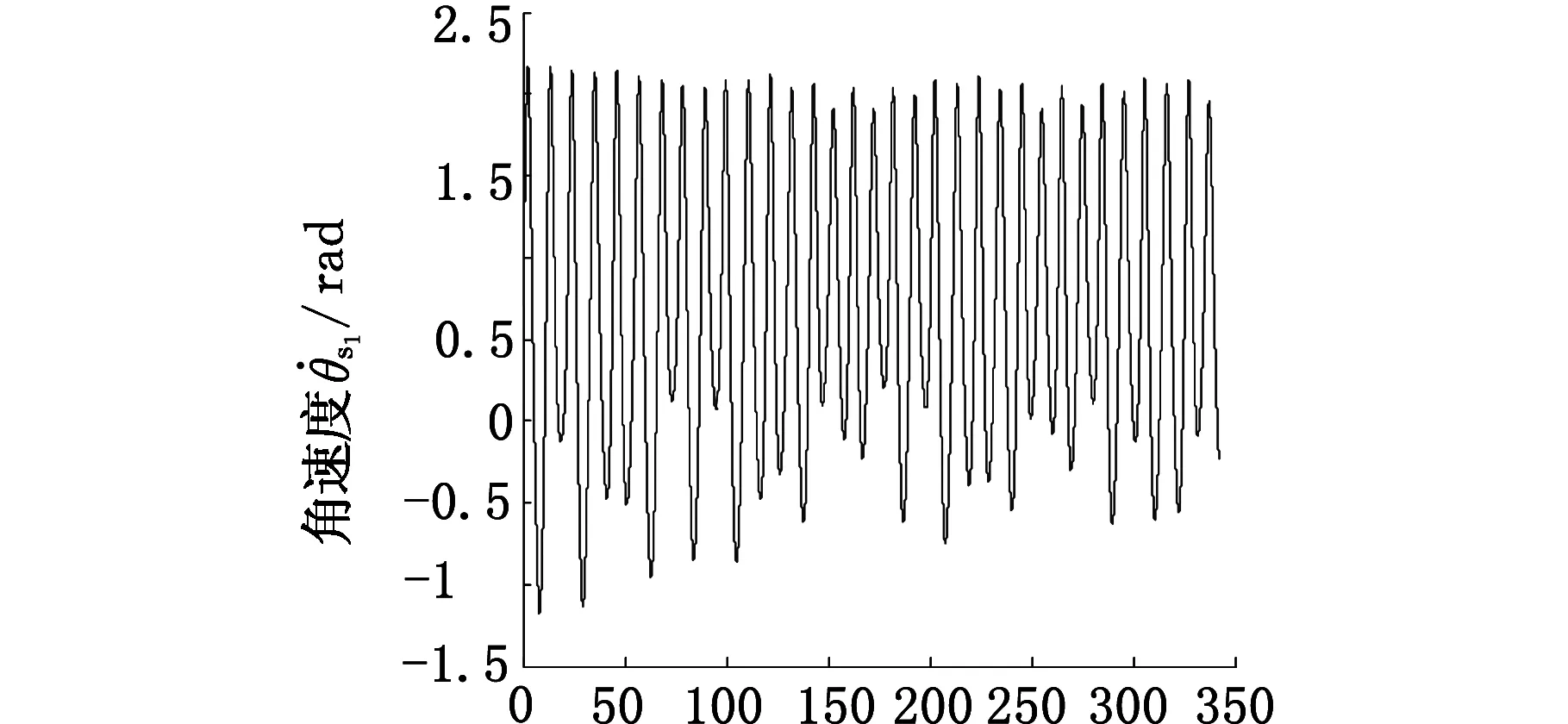
图9 ζ=0.05时太阳轮位移曲线Fig.9 The sun gear displacement curves(ζ=0.05)

3.2 不同啮合刚度下系统的响应

为了研究不同啮合刚度下系统的响应，令其余参数不变，啮合变化系数σ分别为0.2、0.5、0.8，对此三种情况进行求解模拟，其结果如图12～图14所示。

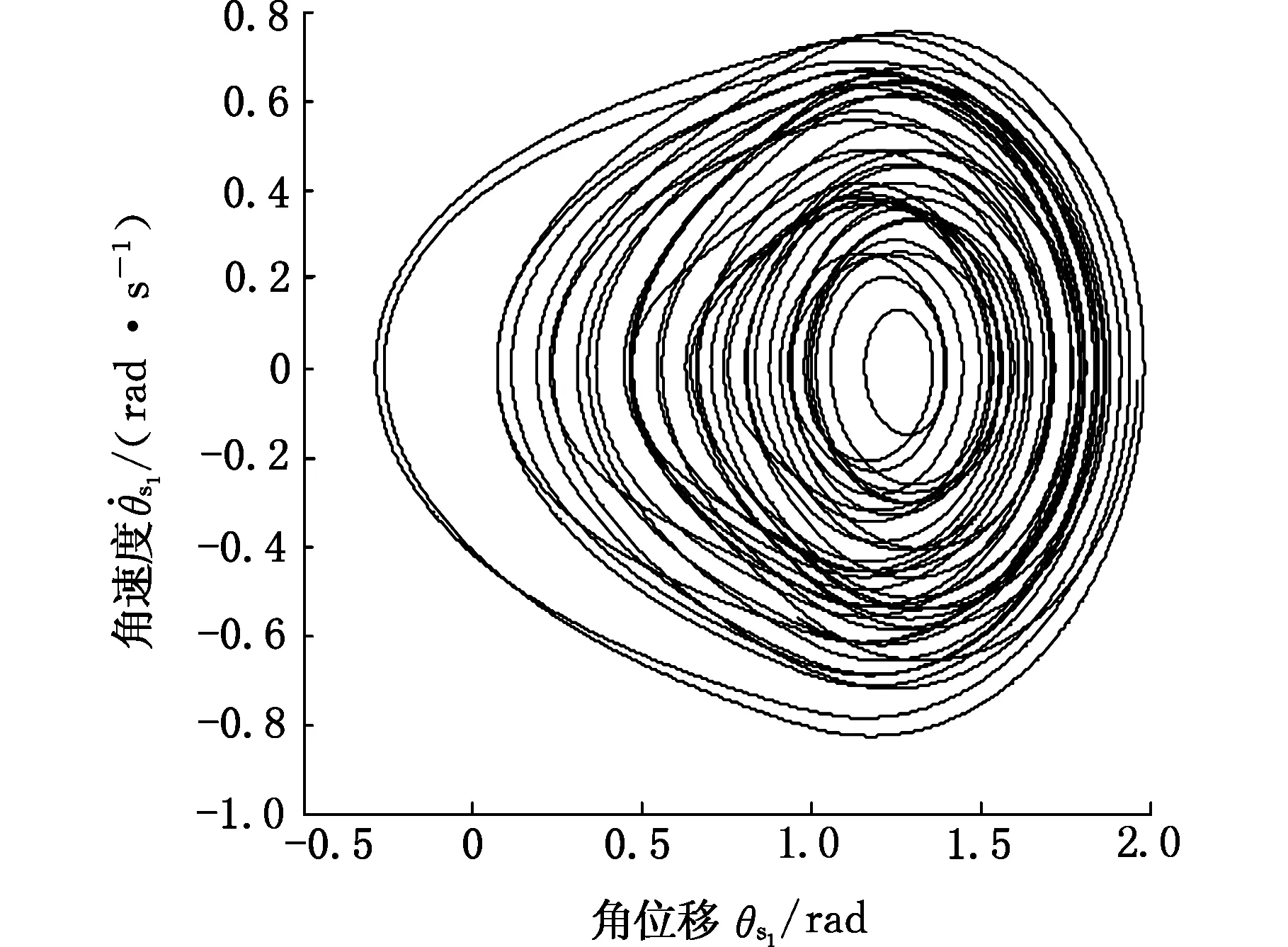
图10 ζ=0.05时太阳轮位移响应相平面图Fig.10 The sun gear displacement response of phase plane diagram(ζ=0.05)

图11 ζ=0.05时太阳轮位移响应庞加莱截面Fig.11 The sun gear displacement response of Poincare section(ζ=0.05)

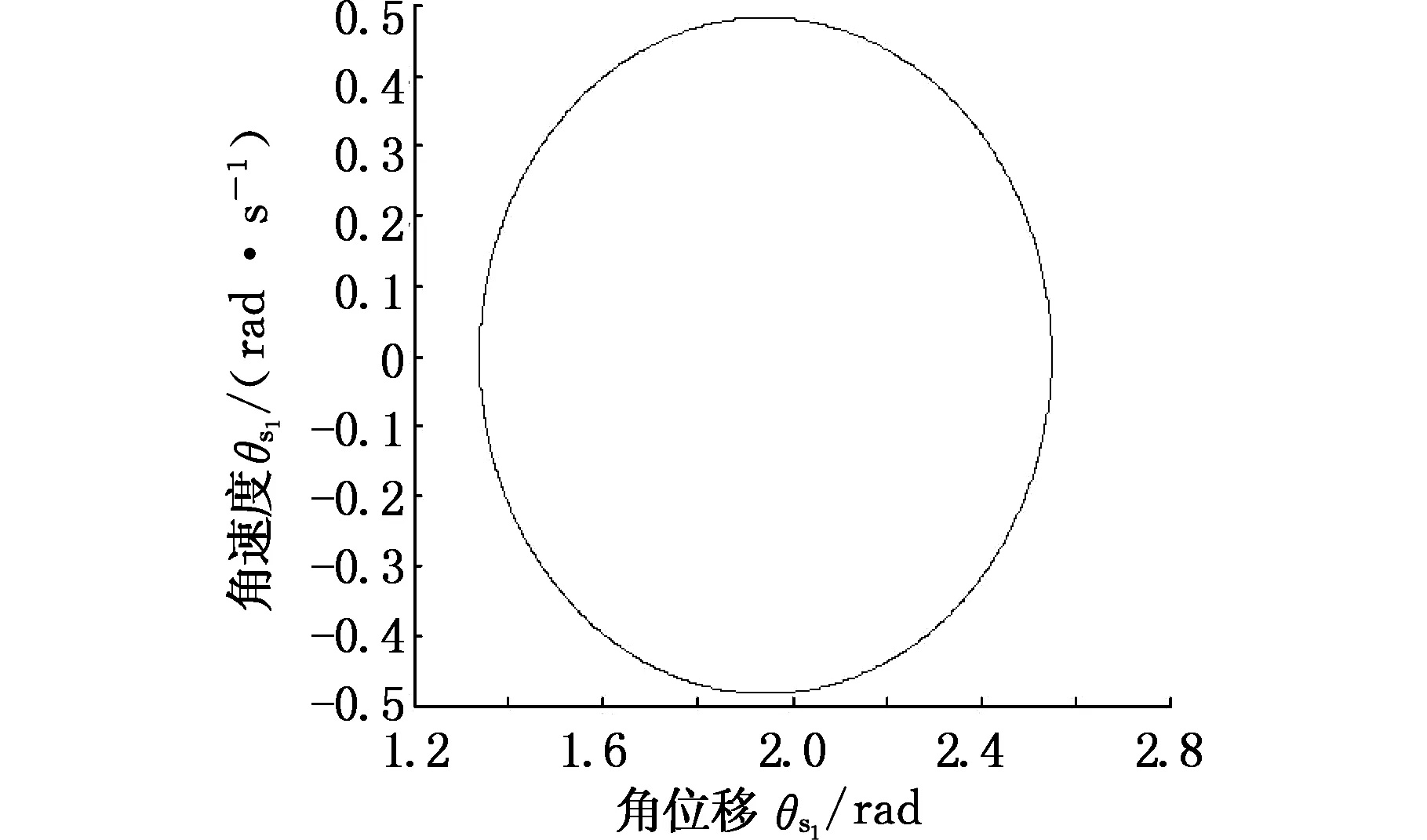
图12 σ=0.2时太阳轮位移响应相平面图Fig.12 The sun gear displacement response of phase plane diagram(σ=0.2)

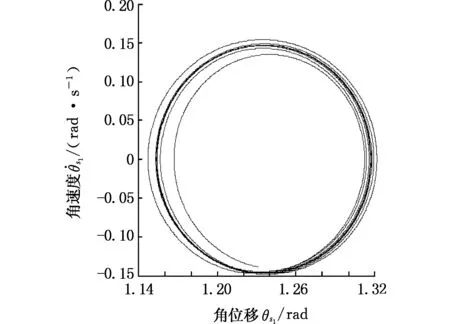
图13 σ=0.5时太阳轮位移响应相平面图Fig.13 The sun gear displacement response of phase plane diagram(σ=0.5)

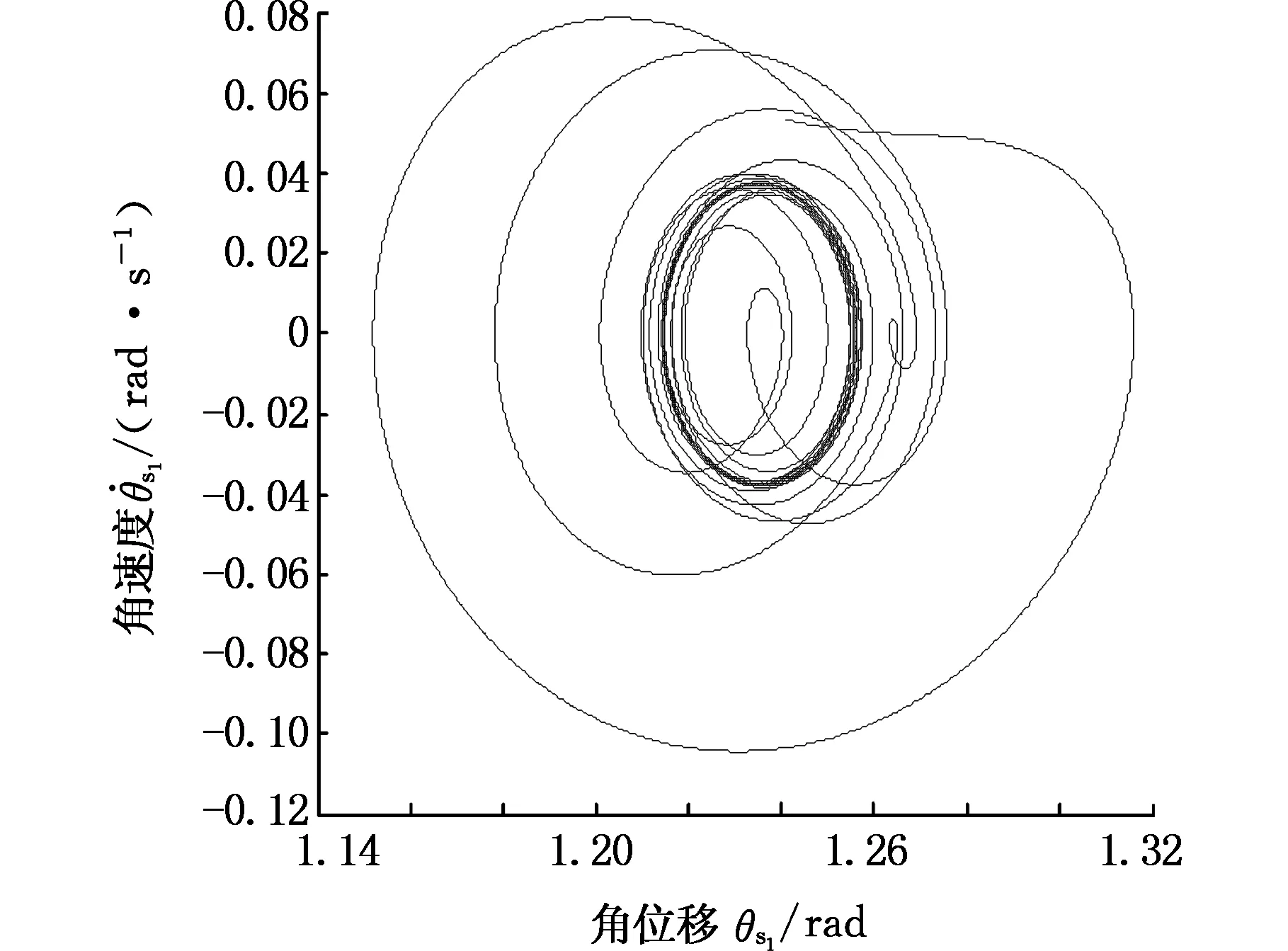
图14 σ=0.8时太阳轮位移响应相平面图Fig.14 The sun gear displacement response of phase plane diagram(σ=0.8)

从图12～图14可知，当σ=0.2时，太阳轮位移响应的相平面图仅存在一个非圆图像，说明太阳轮位移的响应为一个周期运动；当σ=0.5时，太阳轮位移响应的相平面图为6个椭圆，此时齿轮系统的太阳轮位移响应为六周期谐响应；当σ=0.8时，太阳轮位移响应为混沌响应。

3.3 不同激振频率下系统的响应

为了研究不同激振频率下系统的响应，令激振频率Ω的数值分别为0.6、0.8、1.2、1.8，对系统进行求解，得到仿真结果如图15～图22所示。

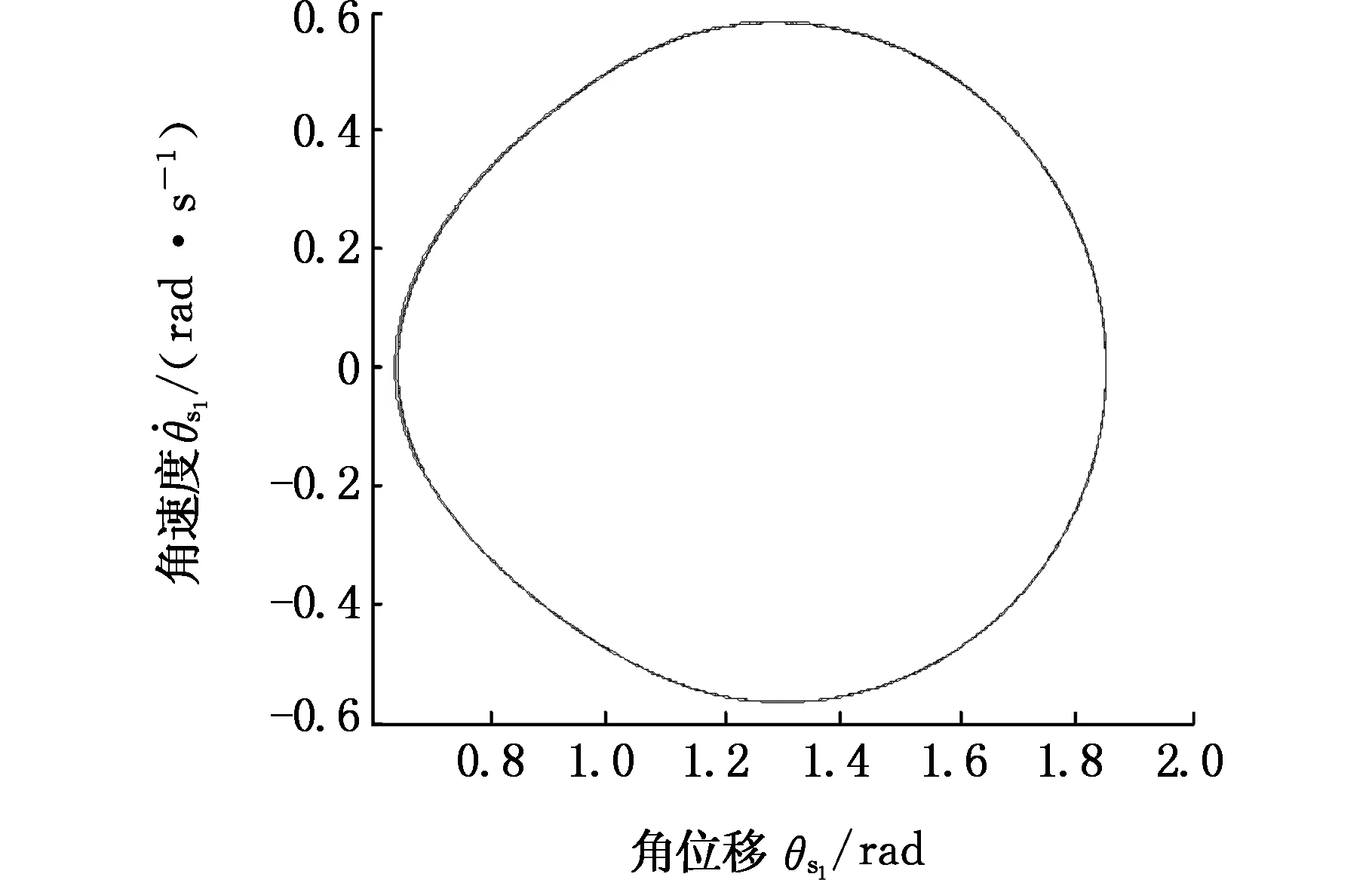
图15 Ω=0.6时太阳轮位移响应相平面图Fig.15 The sun gear displacement response of phase plane diagram(Ω=0.6)

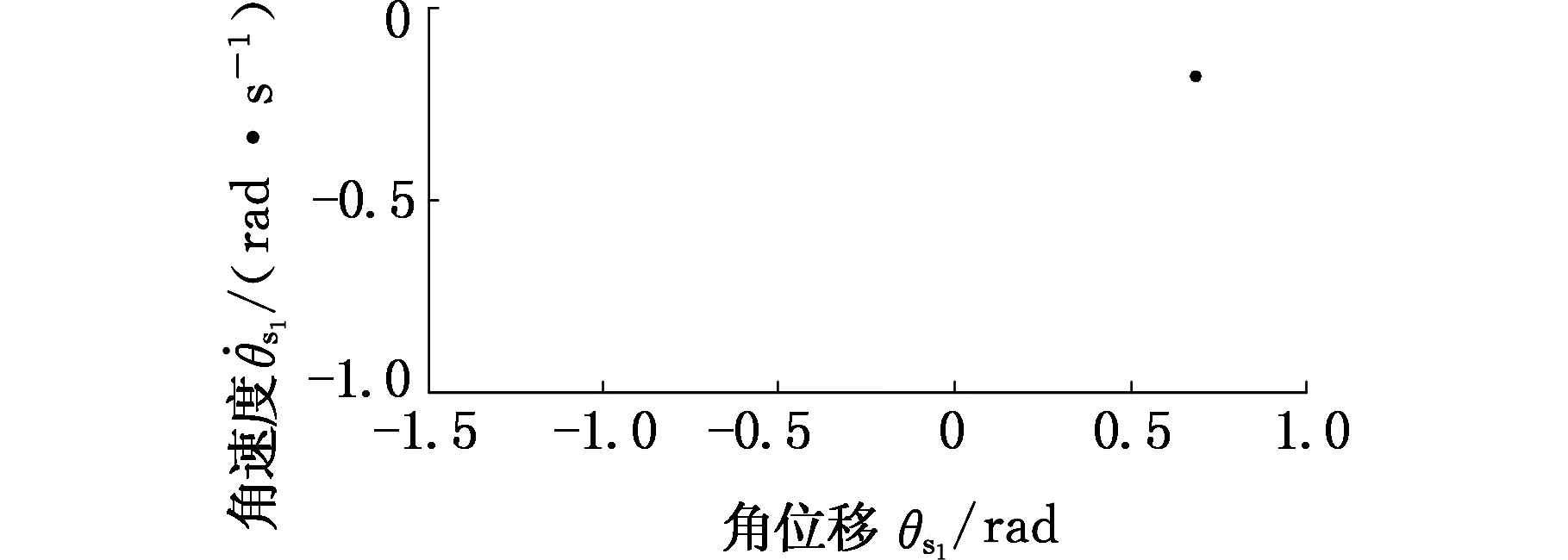
图16 Ω=0.6时太阳轮位移响应庞加莱截面Fig.16 The sun gear displacement response of Poincare section(Ω=0.6)

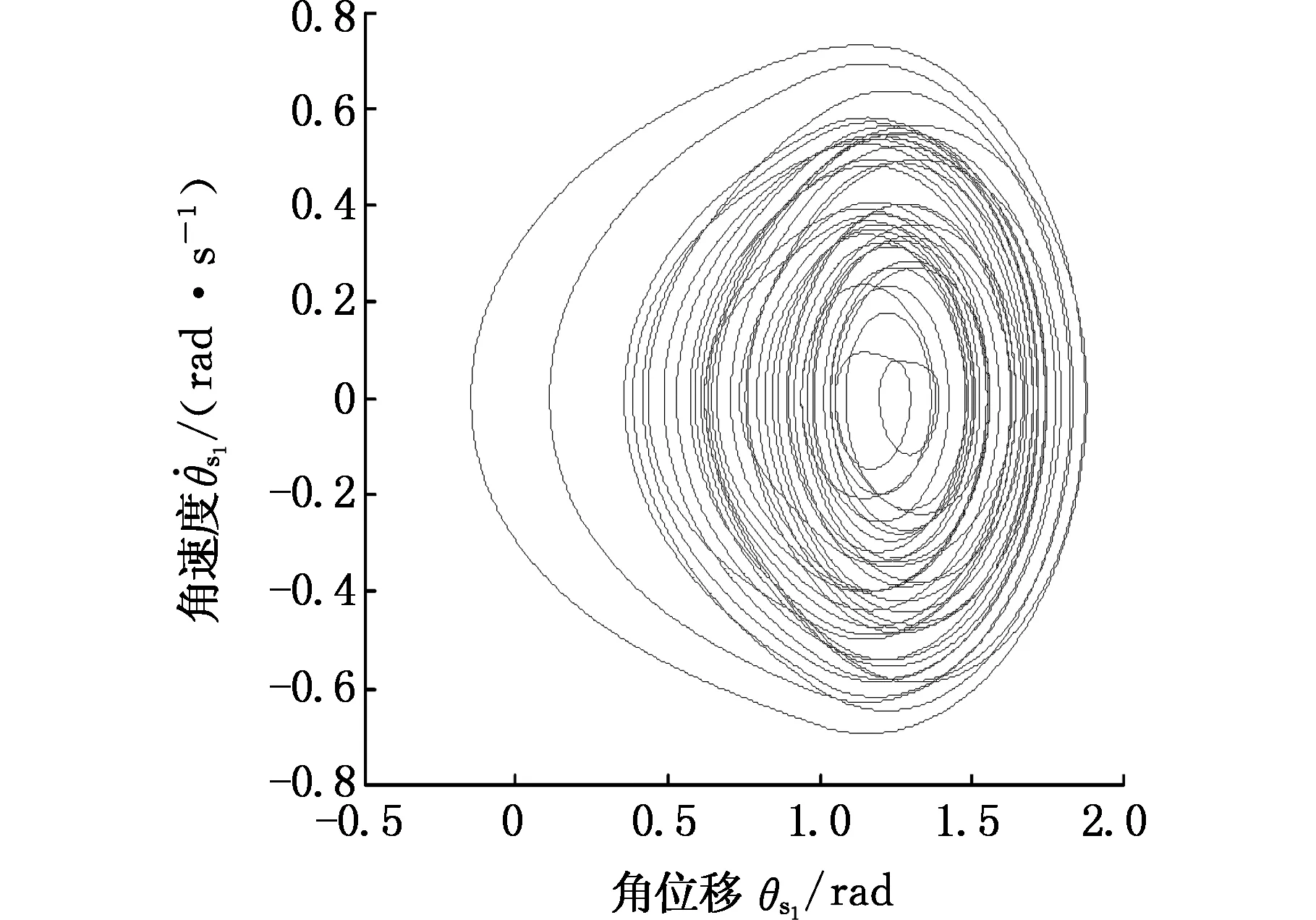
图17 Ω=0.8时太阳轮位移响应相平面图Fig.17 The sun gear displacement response of phase plane diagram(Ω=0.8)

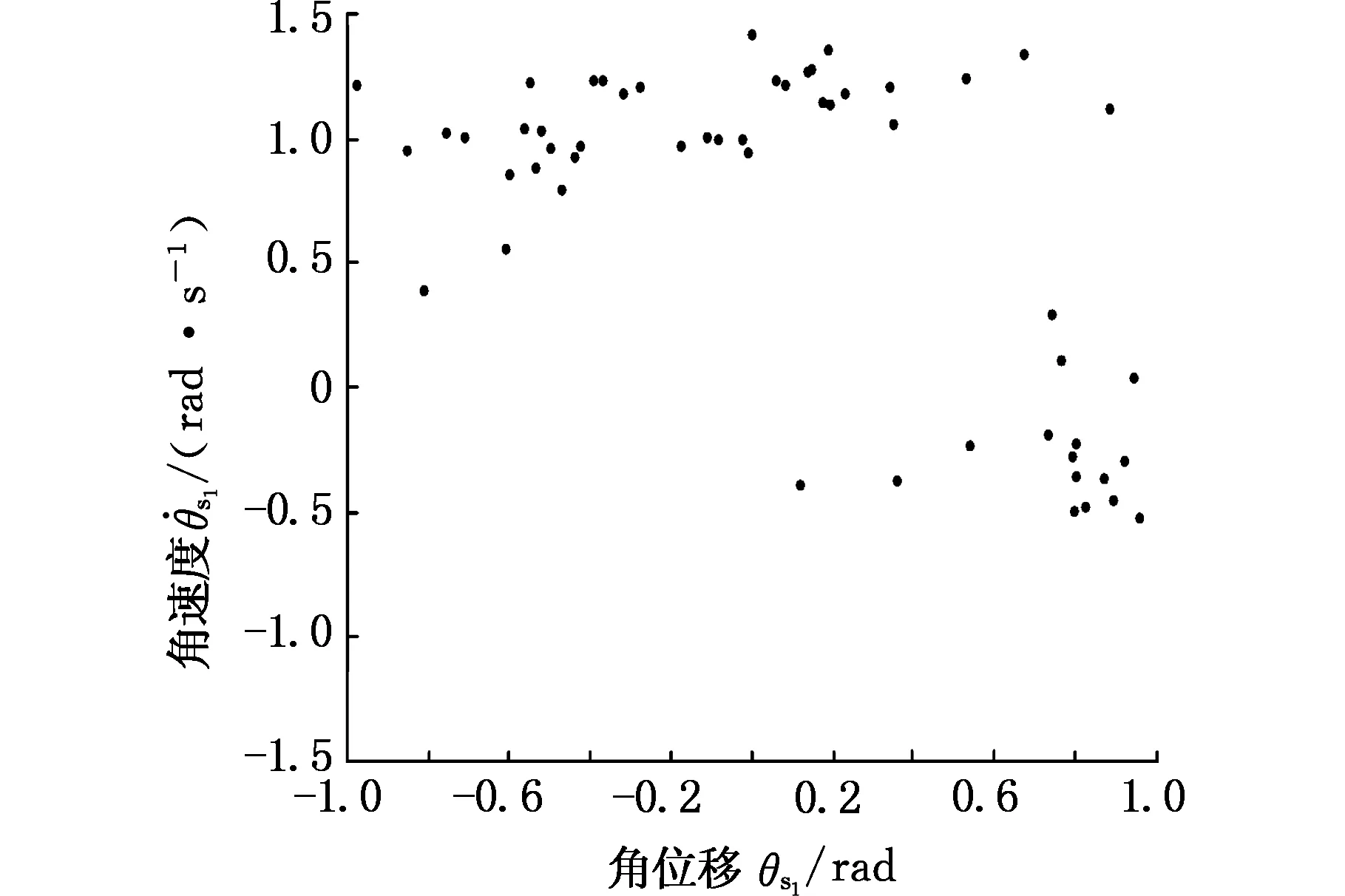
图18 Ω=0.8时太阳轮位移响应庞加莱截面Fig.18 The sun gear displacement response of Poincare section(Ω=0.8)

当激振频率Ω=0.6时，太阳轮位移响应的相平面图仅由一个椭圆构成，且庞加莱截面仅存在一个点，说明此种情况下的响应为周期响应；当Ω=0.8时，庞加莱截面显示为多个截点，此时太阳轮位移响应为混沌响应；当Ω=1.2时，太阳轮位移的相平面图为非椭圆闭合曲线，庞加莱截面为多个离散点聚集在一起，此时太阳轮位移响应为拟周期运动；当Ω=1.8时，太阳轮位移相平面图为两个椭圆，庞加莱截面显示有两个离散点，此时太阳轮位移响应为二周期响应。

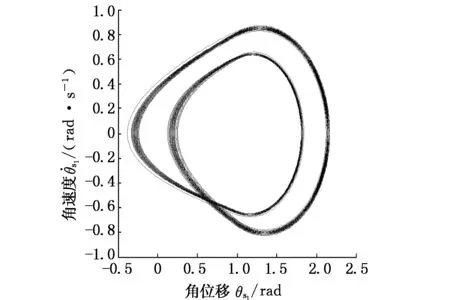
图19 Ω=1.2时太阳轮位移响应相平面图Fig.19 The sun gear displacement response of phase plane diagram(Ω=1.2)

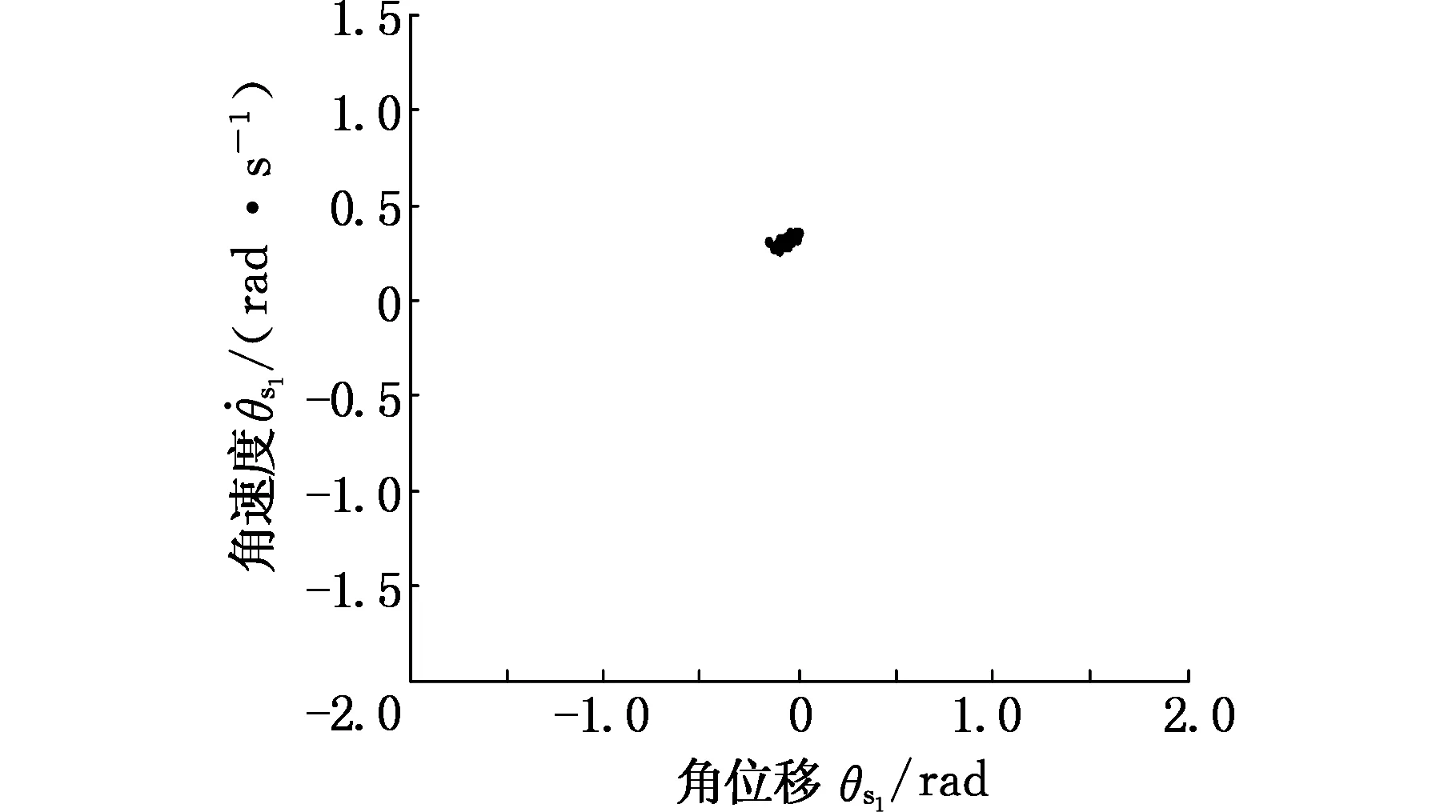
图20 Ω=1.2时太阳轮位移响应庞加莱截面Fig.20 The sun gear displacement response of Poincare section(Ω=1.2)

图21 Ω=1.8时太阳轮位移响应相平面图Fig.21 The sun gear displacement response of phase plane diagram(Ω=1.8)

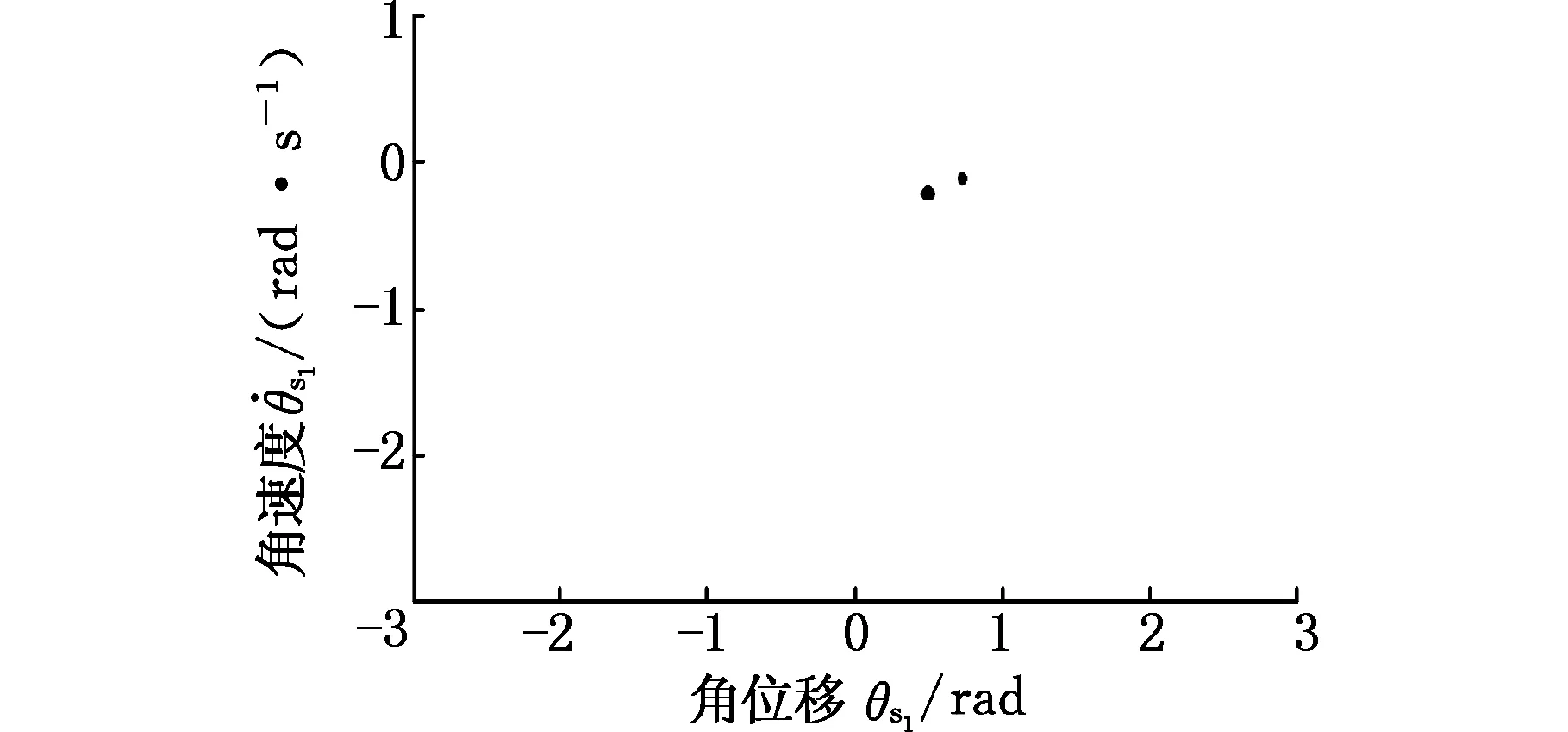
图22 Ω=1.8时太阳轮位移响应庞加莱截面Fig.22 The sun gear displacement response of Poincare section(Ω=1.8)

通过对以上结果分析可知，在一定范围内，当激振频率不断增大时，系统的响应呈现从周期响应状态进入混沌响应再进入拟周期响应状态的规律现象，并非在高激振频率情形下出现混沌现象。

4 结论

本文通过分析采煤机截割部齿轮传动系统的动力学模型，建立其动力学微分方程，运用变步长四阶Runge-Kutta方法对微分方程进行求解，获得该响应的相平面图和庞加莱截面图，通过分析得到以下结论：

在一定区间内，随着阻尼比逐渐减小，行星齿轮系统的太阳轮位移响应由单周期运动变为多周期运动，最终进入混沌运动状态，系统的振动幅度呈增大趋势；啮合刚度对太阳轮位移响应同样产生明显的影响，在一定区间内，啮合刚度增大时，太阳轮位移响应从周期响应进入多周期响应最终进入混沌状态；当激振频率产生变化时，太阳轮位移响应呈现由周期响应转变为混沌响应再转变为拟周期响应的现象。由本文研究结果可知，在一定区间内，增大阻尼比，减小啮合刚度以及在一定范围内，合理地调整激振频率可以有效地降低系统的振动、减小噪声，从而提高采煤机系统的工作可靠性和稳定性。

[1] 赵丽娟，王乘云.采煤机截割部建模与动力学仿真研究[J].工程设计学报，2010，17(2)：119-123. ZHAO Lijuan,WANG Chenyun. Modeling and Dynamic Simulation of Shearer Cutting Unit[J].Journal of Engineering Design, 2010，17(2)：119-123.

[2] 刘送永.采煤机滚筒截割性能及截割系统动力学研究[D].北京：中国矿业大学，2009. LIU Songyong. Research on Cutting Performance of Shearer Drum and Cutting System Dynamics[D].Beijing：China University of Mining and Technology，2009.

[3] LIN J，Parker R G. Planetary Gear Parametric Instability Caused by Mesh Stiffness Variation[J]. Journal of Sound and Vibration, 2002,249(1): 129-145.

[4] BARK C J, PARKER R G. Analytical Solution for the Nonlinear Dynamics of Planetary Gears [J]. Journal of Computational and Nonlinear Dynamics, 2011, 6: 1-15.

[5] ERTIENEL T, PARKER R G. Modal Properties of Three-dimensional Helical Planetary Gears[J].Journal of Sound and Vibration，2009， 35:397-420.

[6] 靳广虎，朱如鹏，鲍和云.正交面齿轮传动系统的非线性振动特性[J].中南大学学报(自然科学版)，2010，41(5)：1807-1813. JIN Guanghu，ZHU Rupeng，BAO Heyun. Nonlinear Dynamical Characteristics of Face Gear Transmiss-ion System[J]. Journal of Central South University(Science and Technology)，2010，41(5)：1807-1813.

[7] 李晓贞，朱如鹏，李政民卿，等.非正交面齿轮传动系统的耦合振动分析[J].中南大学学报(自然科学版)，2013，44(6)：2274-2280. LI Xiaozhen，ZHU Rupeng，LI Zhengminqing，et al. Analysis of Coupled Vibration of Fce Gear Drive with Non-orthogonal Intersection[J]. Journal of Central South University(Science and Technology)，2013，44(6)：2274-2280.

[8] 王世宇，张策，宋轶民，等.行星传动固有特性分析[J].中国机械工程，2005，16(16)：1461-1465. WANG Shiyu，ZHANG Ce，SONG Yimin，et al. Natural Mode Analysis of Planetary Gear Trains[J]. China Mechanical Engineering，2005，16(16)：1461-1465.

[9] SUN Tao，HU Haiyan. Nonlinear Dynamics of a Planetary Gear System with Multiple Clearances[J]. Mechanism and Machine Theory，2003，38(12)：1371-1390.

[10] 公彦军. 齿轮参数对汽车自动变速器动力学性能影响规律的研究[D].合肥：合肥工业大学,2012. GONG Yanjun. Research on the Influence of Gear Parameters to the Dynamic Performance of Automatic Transmission[D]. Hefei ：Hefei University of Technology,2012.

[11] 黄启林. 封闭式行星齿轮传动系统动态特性研究[D].济南：山东大学,2014. HUANG Qilin. Research on Dynamic Characteristics of Closed-form Planetary Gear Train[D]Jinan：Shandong University,2014.

(编辑 袁兴玲)

Nonlinear Dynamics Modeling and Simulation of Shearer Cutting Unit Transmission System

MAO Jun ZHANG Yu ZHANG Kun CHEN Hongyue XU Jianbo

School of Mechanical Engineering, Liaoning Technical University, Fuxin,Liaoning,123000

According to the phenomenon that gear transmission system of shearer cutting unit produced vibrations and noise in operation, a nonlinear dynamics model for gear transmission system of shearer cutting unit was established with the consideration of mesh stiffness, mesh damping, and comprehensive errors. Differential equations were solved by employing variable step size Runge-Kutta integration method. The influences of mesh stiffnesses，damping ratios and excitation frequencies on gear transmission system were studied through analyzing phase plane and Poincare section. The results show that in a certain range，displacement response of sun gear changes from single periodic motion to multi-periodic motion and then into chaotic motion with the decreasing of damping ratio. Displacement response of sun gear also gradually changes from periodic motion to chaotic motion with the increasing of mesh stiffness. Displacement response of sun gear changes from periodic response to chaotic response and then into quasi-period response with the increasing of the excitation frequencies.

shearer cutting unit; planetary transmission system; nonlinear dynamics; dynamics differential equation

2015-12-02

辽宁省教育厅创新团队资助项目(LT2013009)

O121.8

10.3969/j.issn.1004-132X.2017.01.005

毛 君，男，1960年生。辽宁工程技术大学机械工程学院教授、博士研究生导师。主要研究方向为机械动态设计及仿真、机电一体化。E-mail:maojun0828@263.net。张 瑜，男，1987年生。辽宁工程技术大学机械工程学院博士研究生。张 坤(通信作者)，男，1990年生。辽宁工程技术大学机械工程学院硕士研究生。陈洪月，男，1982年生。辽宁工程技术大学机械工程学院副教授。徐建博，男，1989年生。辽宁工程技术大学机械工程学院硕士研究生。